Похожие презентации:
Скалярное произведение векторов. Вычисление углов между векторами
1. Скалярное произведение векторов. Вычисление углов между векторами.
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕВЕКТОРОВ.
ВЫЧИСЛЕНИЕ УГЛОВ МЕЖДУ
ВЕКТОРАМИ.
2. Угол между векторами
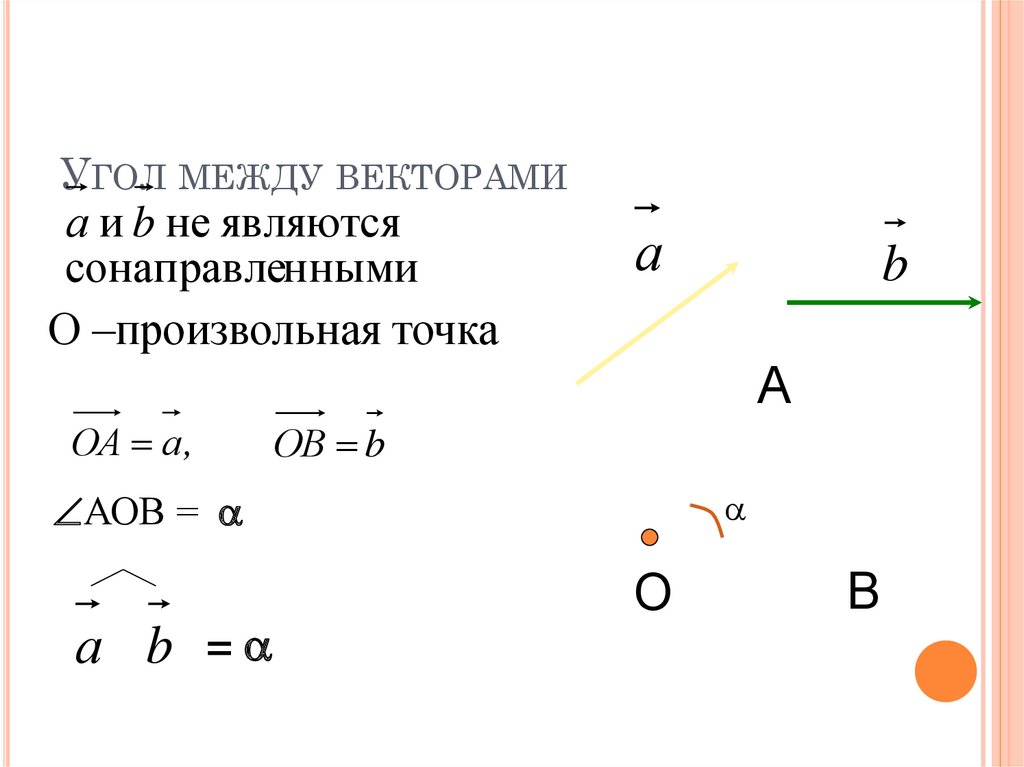
УГОЛ МЕЖДУ ВЕКТОРАМИа и b не являются
сонаправленными
О –произвольная точка
а
b
А
ОА а ,
ОВ b
АОВ =
а b =
О
В
3. Угол между векторами
УГОЛ МЕЖДУ ВЕКТОРАМИЕсли
векторы а и b
сонаправлены, в
частности один из
них или оба
нулевые, то угол
между векторами
равен 0°.
Два вектора
называются
перпендикулярным
и, если угол между
ними равен 90°
а
b
а
а b = 0°
b а b
= 0°
а b = 90°
а
b
а b
4. Найдите угол меду векторами
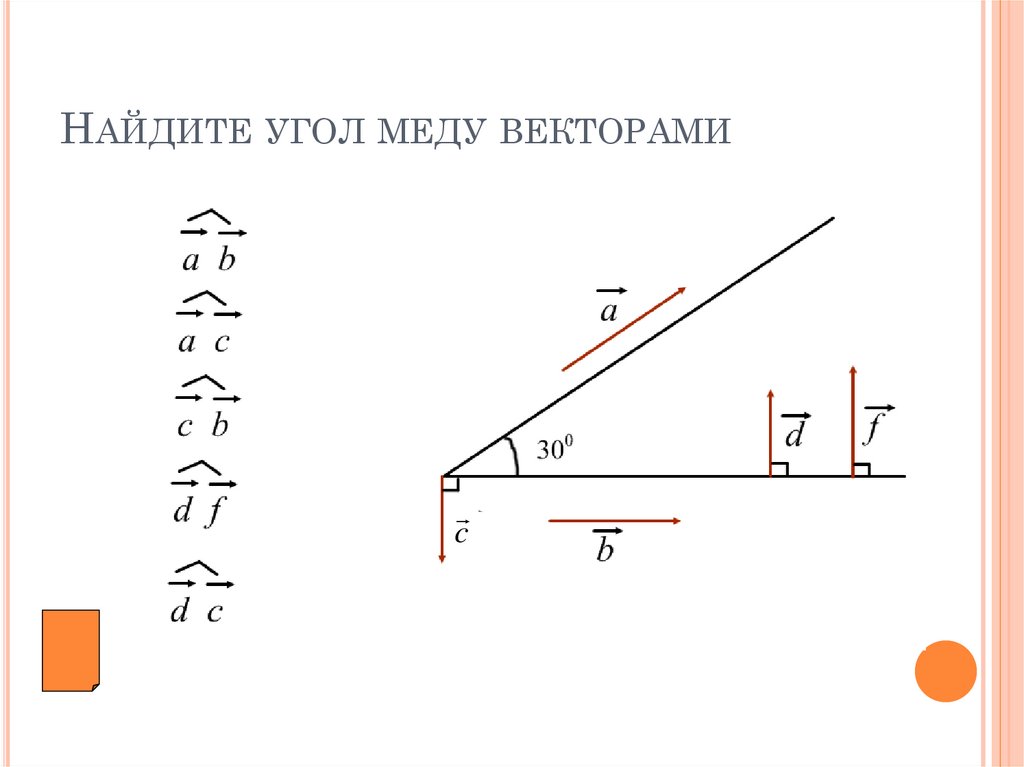
НАЙДИТЕ УГОЛ МЕДУ ВЕКТОРАМИc
5.
0a; b 30 ; a; c 1200
0
0
b ; c 90 ; d ; f 0 d ; c 1800
a b , если 900
a
d
300
c
b
f
6.
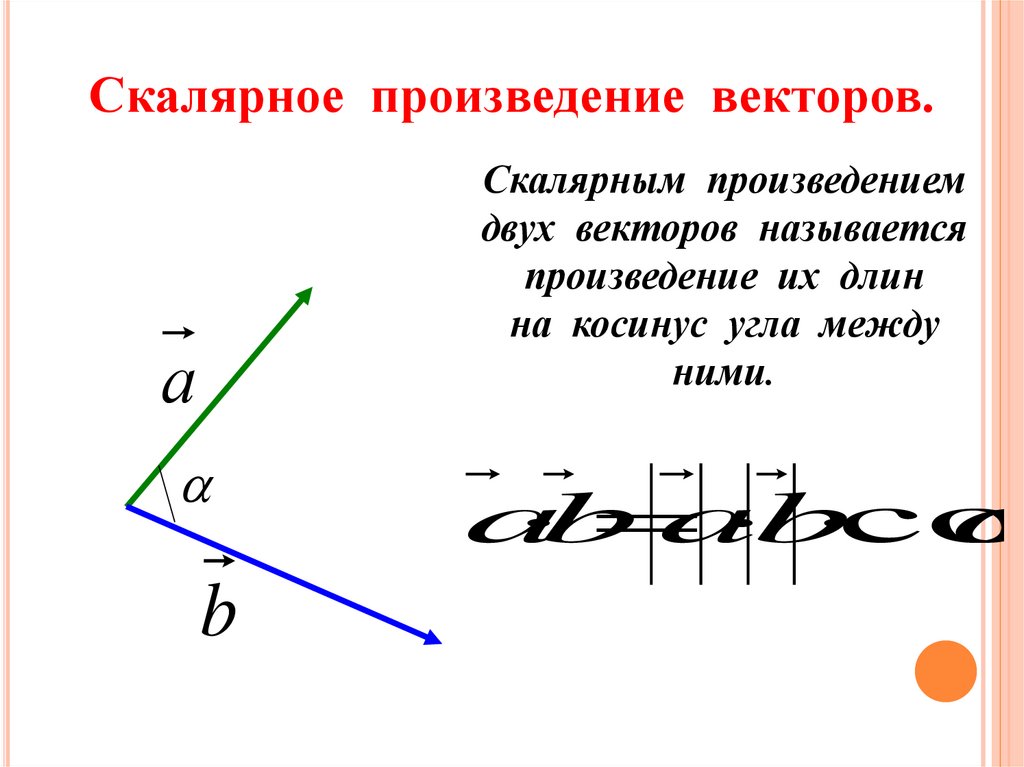
Скалярное произведение векторов.Скалярным произведением
двух векторов называется
произведение их длин
на косинус угла между
ними.
а
b
a
b
a
b
cos
7.
ab a b cos
Если
Если
Если
a b = 0
a b 0
, то
a b
- острый угол
a b 0 , то - тупой угол
, то
8.
Формула скалярного произведениявекторов в пространстве.
а x1;y1;z1
b x2;y2;z2
a
b
x
x
y
y
z
z
12
12
12
Скалярное произведение двух векторов равно
сумме произведений соответствующих
координат этих векторов.
9.
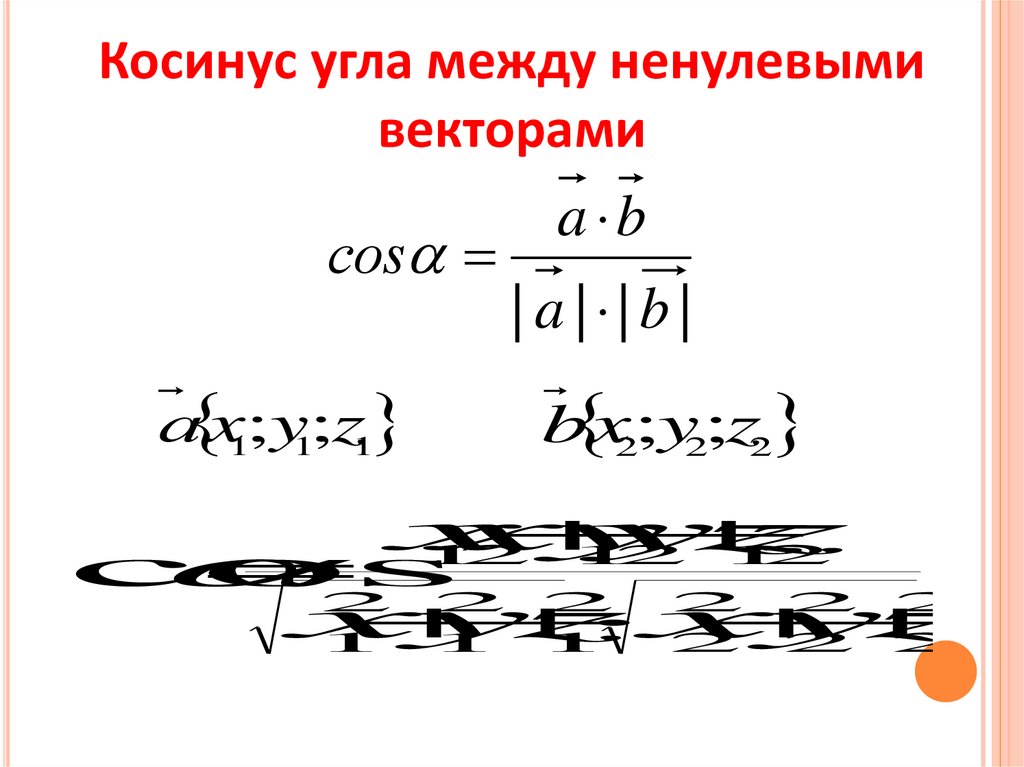
Косинус угла между ненулевымивекторами
соs
а x1;y1;z1
a b
| a | |b |
b x2;y2;z2
x
x
y
y
z
z
1
2 1
2 1
2
cos
2 2 2
2 2 2
x
y
z
x
y
z
1 1 1
2 2 2
10.
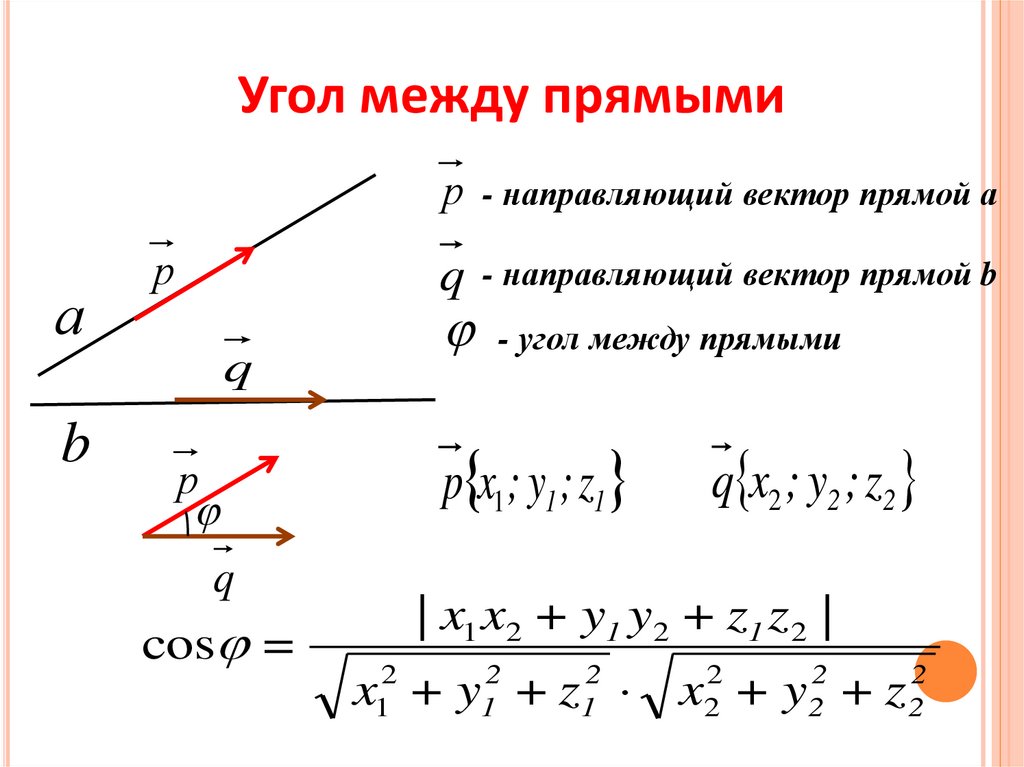
Угол между прямымиа
р
q
b
р
q
cos =
р
- направляющий вектор прямой а
q
- направляющий вектор прямой b
- угол между прямыми
p x1 ; y1 ; z1
q x2 ; y2 ; z2
| x1 x2 + y1 y2 + z1 z 2 |
x12 + y12 + z12 x22 + y22 + z 22
11. пример
ПРИМЕРa 2 , b 3,
угол между векторами а и b
1350
a b a b cos
2
a b 2 3 cos 135 6 cos 45 6
3 2
2
0
0
12. Необходимое и достаточное условие равенства нулю скалярного произведения
НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕРАВЕНСТВА НУЛЮ СКАЛЯРНОГО
ПРОИЗВЕДЕНИЯ
Скалярное произведение ненулевых
векторов равно нулю тогда и только тогда
когда эти векторы перпендикулярны
1
a 0
b 0 a b 0
a b
2
a 0
b 0 a b
a b 0
13. Скалярный квадрат
СКАЛЯРНЫЙ КВАДРАТСкалярное произведение
a a
называется скалярным квадратом вектора
a a a a cos a a
cos a a соs 00 1
a a a a а
2
a
a
Свойство.
Скалярный квадрат вектора равен квадрату его длины.
14. Самое главное
САМОЕ ГЛАВНОЕСкалярным произведением векторов
называется произведение их длин на косинус
угла между ними
Скалярное произведение ненулевых векторов
равно нулю тогда и только тогда когда эти
векторы перпендикулярны
Скалярное произведение вектора самого на
себя называется скалярным квадратом вектора
Скалярный квадрат вектора равен квадрату
его длины.
15.
16.
17.
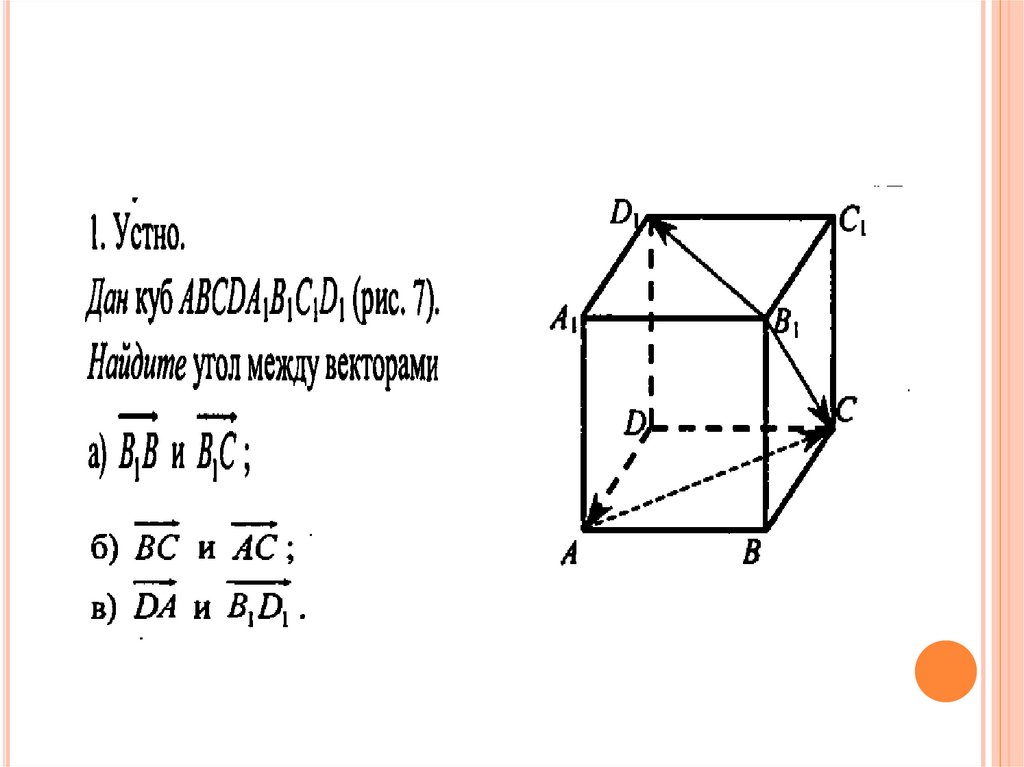
Решение задач№ 464(б)
Вычислить угол между прямыми AB и CD, если
A(5;-8;-1), В(6;-8;-2), С(7;-5;-11), D(7;-7;-9)
Решение
AB 1;0; 1
cos =
СD 0; 2;2
| 1 0 0 ( 2) ( 1) 2 |
12 0 2 ( 1) 2 0 2 ( 2) 2 2 2
1
cos
2
60
0
18.
№ 464(в)Вычислить угол между прямыми AB и CD, если
A(1;0;2), В(2;1;0), С(0;-2;-4), D(-2;-4;0)
Решение
AB 1;1; 2
СD 2; 2;4
Так как координаты векторов пропорциональны,
то векторы коллинеарны, а прямые параллельны.
0
0



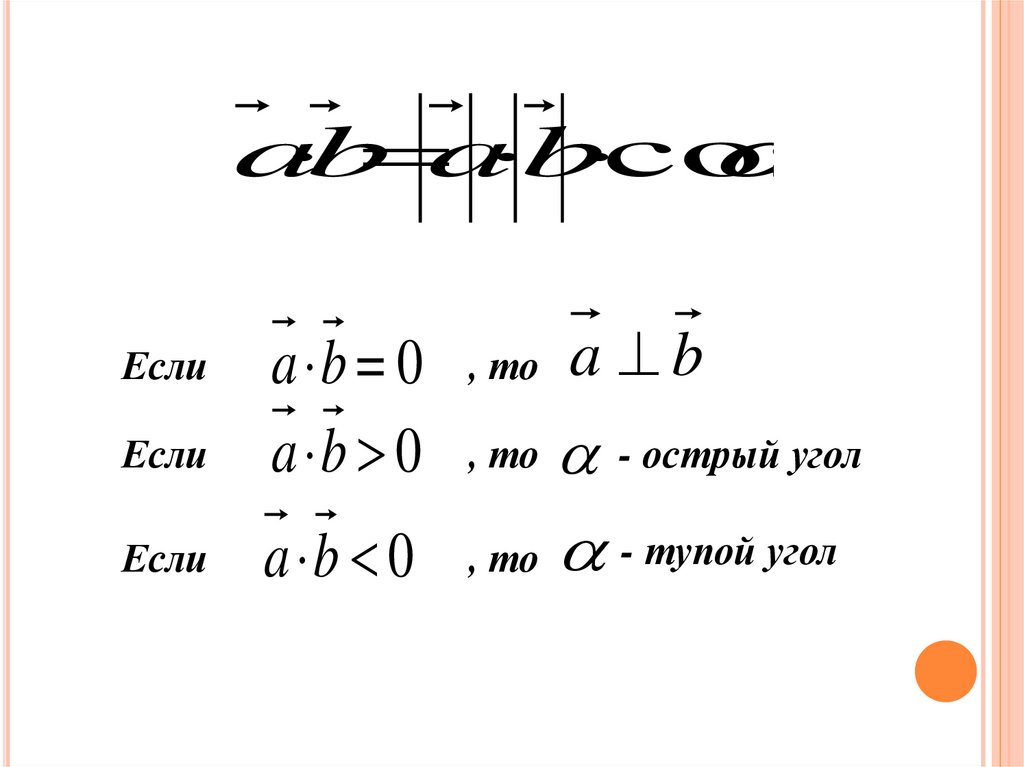








 Математика
Математика








