Похожие презентации:
Классическая статистическая теория идеального газа. Тема 11
1.
Тема 11: Классическая статистическаятеория идеального газа
Учебные вопросы:
1. Основное уравнение молекулярнокинетической теории идеального газа
2. Теплоемкость идеального газа
3. Распределения Максвелла и Больцмана
1
2.
ВведениеПри молекулярно-кинетическом подходе к исследованию физических тел как
совокупности большого числа движущихся молекул макроскопические свойства
тела определяются как результат этого движения. Рассмотрение молекулярного
движения возможно с двух принципиально различных точек зрения:
1. Детерминированный подход – движение каждой молекулы рассматривается на
основании законов динамики Ньютона. Однако подобный динамический метод
исследования практически неприменим из-за исключительно большого числа
образующих тело частиц ( в одном кубическом сантиметре идеального газа в
нормальных условиях содержится 2,687 1019 молекул).
2. Теоретико-вероятностный подход – движение молекул рассматривается как
случайный процесс, характеризуемый в любой момент времени некоторыми
распределениями вероятностей для координат и скоростей молекул. Если состояние
является установившимся (равновесным), то среднее по времени полагается
равным среднему по множеству (эргодическая гипотеза Больцмана) и,
следовательно, средние параметры, характеризующие случайное движение каждой
2
молекулы, могут быть найдены в результате усреднения соответствующих
параметров всех молекул в любой момент времени.
3.
Операции нахождения средних значений по совокупности данных ослучайных явлениях являются инструментом математической статистики,
поэтому соответствующий метод исследования физических систем получил
название статистического метода.
Статистическая физика – раздел физики, в котором изучаются
общие свойства макроскопических физических систем в состоянии
термодинамического равновесия на основе теоретико –
вероятностной интерпретации молекулярного движения и применения
методов математической статистики.
3
4.
1. Основное уравнение молекулярнокинетической теории идеального газаСредняя кинетическая энергия и средняя скорость поступательного
движения молекул
Пусть в равновесном состоянии находится система из N одинаковых молекул
с массой m0 . Кинетическая энергия поступательного движения i- ой молекулы равна
пост .
кi
W
1
2
= m0ui
2
(1)
4
5.
Средняя кинетическая энергия всех N молекул равнапост .
к
W
1
=
N
N
åW
i =1
пост
кi
1 æ1
= m0 ç
2 èN
ö
u ÷=
å
i =1
ø
N
2
i
1
1
2
2
= m0 u = m0u скв
2
2
Величина
u скв =
u
2
=
1
N
(2)
N
åu
i =1
2
i
(3)
называется средней квадратичной скоростью молекул газа.
5
6.
Уравнение КлаузиусаБудем считать, что молекула представляет
r собой материальную точку массой
m0
, движущуюся
со скоростью .
u
Тогда при абсолютно упругом ударе о стенку молекула передаст стенке импульс, равный
r
u
ux
k = 2m0u x
x
r
u
ux
Рассмотрим молекулы, для которых проекция вектора
скорости на ось 0x положительна и находится в пределах
от u x до u x + Du x .
Обозначим число таких молекул в единице объема через
Dn(u x ).
Тогда за время Dt до участка стенки площадью S долетят и столкнутся с ней
только те молекулы, которые находятся внутри слоя объемом V (u x ) = S u, x Dt
прилегающего к этому участку.
6
7.
Число таких молекул равноDN = Dn (u x ) S u x ,Dt
а передаваемый ими стенке импульс равен
K = k DN = (2m0u x ) ( Dn(u x ) Su x Dt )
K = F Dt
p=F S
давление на стенку данной группы молекул DN
Поскольку
а давление газа
равно
Dp(u x ) = 2m u Dn(u x )
2
0 x
(4)
Суммарное давление, оказываемое на стенку всеми подлетающими молекулами,
будет равно сумме давлений (4) по всем группам молекул:
p = 2m0 å u Dn(u x )
u x >0
2
x
(5)
7
8.
В соответствии с гипотезой о хаотичности молекулярного движения в положительномнаправлении оси Ох
движется половина всех молекул газа
1
1
2
2
u Dn(u x ) = åu x Dn(u x ) = n u x
å
2
2
u >0
2
x
(6)
x
где
n - концентрация молекул.
Отсюда следует, что
p = m0n u
2
x
(7)
В силу равноправия всех направлений движения молекул вдоль
осей x, y и z
u
2
x
1 2
= u
3
(8)
8
9.
С учетом этого получимm
u
1
2
0
2
p = m0n u = n
3
2
3
2
2
пост .
= n Wк
3
(9)
Следствия из уравнения Клаузиуса
Следствие первое.
Следовательно
пост .
к
W
2
пост .
nkT = n Wк
3
3
= kT
2
(10)
(11)
Средняя кинетическая энергия поступательного теплового движения молекул
идеального газа определяется только его термодинамической температурой и не
зависит от массы молекул.
9
10.
Отсюда следует важный вывод:Термодинамическая температура идеального газа является количественной
мерой кинетической энергии теплового поступательного движения его молекул:
Следствие второе.
2
пост .
T=
Wк
3k
Умножая равенство (10) на объем газа, и поскольку
(12)
nV = N
2
2
пост .
= U1
pV = N Wк
3
3
получим:
(13)
Произведение давления газа на его объем равно 2 3 кинетической энергии
хаотического поступательного движения всех его молекул.
10
11.
Следствие третье.Сопоставляя (2) и (11),
пост .
ì пост.
2 Wк
1
2
2
= m0u скв Þ u скв =
ï Wк
ï
2
m0
í
3
ï
пост .
Wк
= kT
ïî
2
получим, что средняя квадратичная скорость молекул равна:
u скв =
u
2
kT
RT
= 3
= 3
m0
M
(14)
11
12.
Средние квадратичные скорости молекул некоторых газов при нормальных условиях:газ
H2
He
N2
воздух
O2
CO 2
M 103, кг/моль
2
4
28
29
32
44
1845
1304
493
485
461
393
uскв , м/с
12
13.
2. Теплоемкость идеального газаСтепени свободы молекул
Внутренняя энергия идеального газа
U = U1 + U 2 + U 3
где
(15)
U1 - кинетическая энергия поступательного, U 2 - кинетическая энергия
вращательного движения молекул, а U 3 - кинетическая и потенциальная
энергия колебательного движения атомов внутри молекул.
Молекулу газа можно рассматривать как систему материальных точек (атомов),
связанных друг с другом упругими линейными связями.
Обозначим через
iпост , iвращ , iколеб
число степеней свободы поступательного, вращательного и колебательного ее
движений.
13
14.
Примеры молекулОдноатомный газ
iпост = 3, iвращ = 0, iколеб = 0
(16)
Двухатомный газ
iпост = 3, iвращ = 2, iколеб = 1
(17)
Трехатомный газ
iпост = 3, iвращ = 3, iколеб = 3
(18)
14
15.
Закон Больцмана о равномерном распределении энергиипо степеням свободы молекул
Для макроскопической системы, состоящей из большого числа
хаотически движущихся молекул,
в состоянии термодинамического
равновесия при отсутствии внешних силовых полей в среднем на каждую
поступательную и вращательную степень свободы молекулы приходится
энергия, равная kT 2 , а на каждую колебательную степень свободы –
энергия, равная kT .
В соответствии с этим законом средняя энергия молекулы определяется
выражением:
где
i
W = kT
2
(19)
i = iпост + iвращ + 2iколеб
(20)
15
16.
Внутренняя энергия одного моля газа равна:U м = CV T
(21)
С другой стороны, внутренняя энергия одного моля газа равна
i
U м = N A W = RT
2
Следовательно
(22)
i
CV = R
2
В соответствии с теоремой Майера молярная теплоемкость газа при
постоянном давлении равна
а показатель адиабаты
i+2
Cp = C V +R =
R
2
Cp i + 2
g =
=
CV
i
(23)
(24)
(25)
16
17.
3. Распределения Максвелла и БольцманаРаспределение молекул по проекциям вектора скорости
y
Пусть молекула
идеального
газа
движется
со
r
скоростью u в произвольно ориентированной
декартовой системе координат.
r
u
Рассмотрим проекции вектора скорости молекулы на
оси произвольно ориентированной декартовой системы
координат
uy
z
r
u
ux
uz
O
x
O
Проекции вектора скорости молекулы представляют
собой независимые случайные величины, одинаково
распределенные по нормальному закону (закону Гаусса).
17
18.
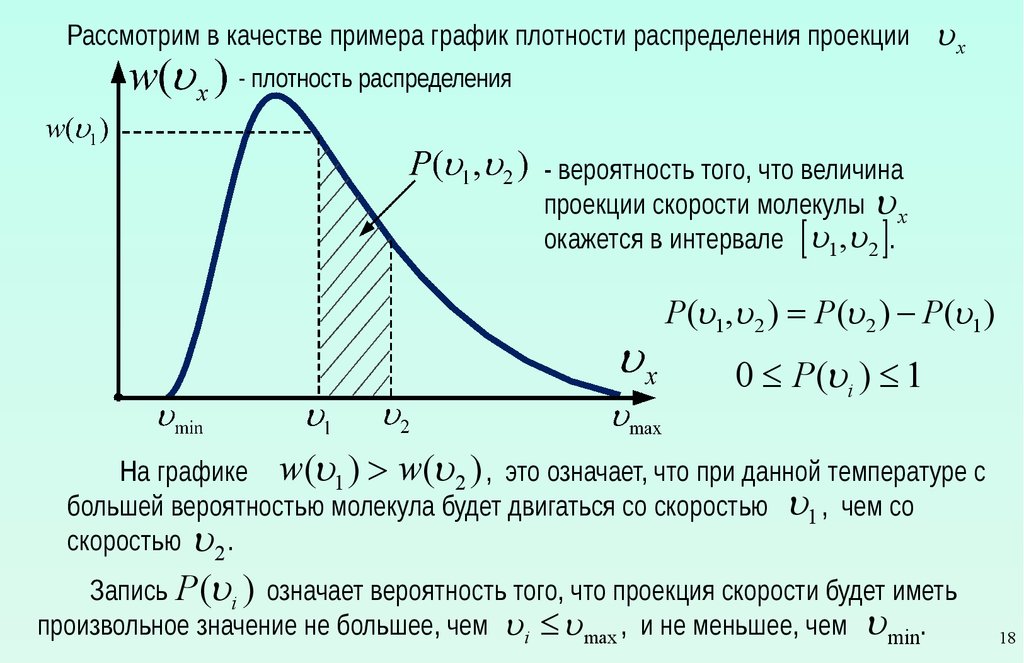
Рассмотрим в качестве примера график плотности распределения проекцииux
- плотность распределения
- вероятность того, что величина
проекции скорости молекулы u x
окажется в интервале [ u1 ,u 2 ].
P (u1 ,u 2 ) = P(u 2 ) - P(u1 )
0 £ P(ui ) £ 1
На графике w(u1 ) > w(u 2 ) , это означает, что при данной температуре с
большей вероятностью молекула будет двигаться со скоростью u1 , чем со
скоростью u 2 .
Запись P (ui ) означает вероятность того, что проекция скорости будет иметь
произвольное значение не большее, чем ui £ u max , и не меньшее, чем u min.
18
19.
Плотности распределения проекцийравны соответственно:
w(u x ) = Ae
где
- bu x2
u x , u y , u z вектора скорости молекулы
, w(u y ) = Ae
m0
b=
,
2kT
- bu 2y
, w(u z ) = Ae
- bu z2
b
m0
A=
=
p
2p kT
r
u
(26)
(27)
r
du , которое также имеет свои
Рассмотрим далее приращение вектора скорости
проекции du x , du y и du z . Вероятность того, что значение вектора скорости окажется
r
в пределах параллелепипеда с гранями du x , du y , du z (или
uy
du
вероятность того, что значения проекций вектора скорости
r
u
находятся в пределах [u x ,u x + du x ), [u y ,u y + du y ), [u z ,u z + du z ),
ux
равна
uz O
du y
du z
du x
dP (u x ,u y ,u z ) = dP(u x )dP(u y )dP(u z )
19
20.
гдеdP(u x ) = w ( u x ) du x , dP (u y ) = w ( u y ) du y , dP(u z ) = w ( u z ) du z
следовательно
2
2
2
3 - b (u x +u y +u z )
dP (u x ,u y ,u z ) = A e
du x du y du z
(28)
Число молекул, для которых конец вектора скорости в пространстве скоростей
находится в элементарном объеме du x du y du z , расположенном в точке с
координатами (u x ,u y ,u z )
dN (u x ,u y ,u z ) = NdP (u x ,u y ,u z )
(29)
где N - общее число молекул
20
21.
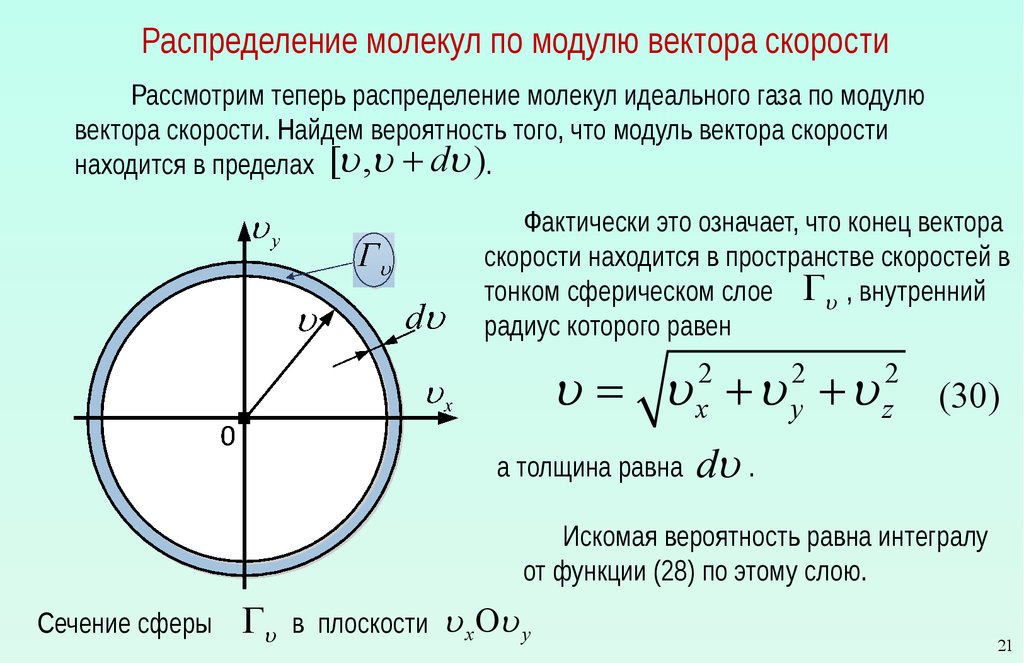
Распределение молекул по модулю вектора скоростиРассмотрим теперь распределение молекул идеального газа по модулю
вектора скорости. Найдем вероятность того, что модуль вектора скорости
находится в пределах [u ,u + du ).
Фактически это означает, что конец вектора
скорости находится в пространстве скоростей в
тонком сферическом слое Gu , внутренний
радиус которого равен
u = u +u +u
2
x
а толщина равна
2
y
2
z
(30)
du .
Искомая вероятность равна интегралу
от функции (28) по этому слою.
Сечение сферы
Gu
в плоскости
u x Оu y
21
22.
Из вида этой функции следует, что она в пределах этого слоя постоянна,поэтому указанный интеграл равен:
3 - bu 2
dP (u ) = A e
d
u
d
u
d
u
=
x
y
z
òòò
Gu
3 - bu 2
=Ae
4pu du
2
а число молекул, имеющих скорость в диапазоне
[u ,u + du ), равно
3 - bu 2
dN (u ) = NdP (u ) = NA e
(31)
4pu du
2
(32)
22
23.
Распределение МаксвеллаПлотность распределения вероятности для модуля вектора скорости молекул
определяется формулой
wА
(u ) = 4ep
3
u
2 - bu 2
(33)
Из (33) следует, что вероятность того, что молекула будет иметь скорость в
диапазоне от u1 до u 2 , равна
u2
PА
(u1 ,u 2 ) =e 4p d ò u
3
соответствующее число молекул равно
2 - bu 2
u
(34)
u1
N (u1 ,u 2 ) = NP (u1 ,u 2 )
(35)
23
24.
w(u )w(u )
T = 173K
T = 273K
T = 373K
T = 473K
u вер
u
u
T
Характерные скорости молекул
Из (33) следует, что максимум распределения Максвелла достигается при значении
скорости
u вер
kT
= 2
m0
(36)
которая называется наиболее вероятной скоростью.
24
25.
Средние значения скорости и ее квадрата равны¥
u = ò u w(u )du ,
0
¥
u 2 = ò u 2 w(u )du ,
0
Вычисления показывают, что средняя скорость равна
8 kT
8 RT
u =
=
,
p m0
p M
а средняя квадратичная
u скв =
При этом
(T = 273,15К)
u , м/с
(37)
u
2
(38)
kT
= 3
m0
u вер : u : u скв = 1:1,13 :1, 22
H2
O2
N2
H 2O
CO 2
1709
427
457
567
364
(39)
(40)
25
26.
4. Распределение молекул по кинетической энергииРассмотрим распределение молекул идеального газа по значению кинетической энергии поступательного движения. С этой целью, используя соотношение
(31), найдем вероятность того, что кинетическая энергия молекулы находится в пределах
[Wк ,Wк + dWк )
.
2Wк
2
Из определения кинетической энергии следует, что
u du =
dWк
3
Подставляя это выражение в (31), получим:
(41)
m0
Wк
kT
, (42)
к
к
к
3
2
dP(W ) =
2
p ( kT )
Wк
a=
kT
(43)
a
a
Рис.6
e
W dW
откуда следует, что плотность вероятности
для распределения молекул по кинетической
энергии в относительных единицах a равна
2
w1 (a ) =
p
При этом
ae
-a
3
a =
2
(44)
(45)
26
27.
Используя формулу (42) найдем относительное число молекул, имеющих кинетическуюэнергию поступательного движения в заданном диапазоне [Wк1 ,Wк 2 ) :
N (Wк1 ,Wк 2 )
2
=
3
N
p ( kT ) 2
Wк 2
òe
Wк 1
Wк
kT
æ Wк 2 ö
æ Wк1 ö
Wк dWк = F ç
÷-Fç
÷
è kT ø
è kT ø
2
F ( z) =
p
для которых
Wк
£z
kT
z
ò
a e -a d a
(46)
(47)
0
График функции (47) показан на рис.7.
z
Рис.7
-
Из рис. 6 и 7 видно, что энергия молекул
в основном не превышает 8kT (при комнатной температуре 8kT » 0, 2эВ ) .
Средняя энергия молекул равна 1,5kT ,
в диапазоне (1 ¸ 2)kT находятся 31%, а
в диапазоне (0,5 ¸ 2,5)kT - 63% всех
молекул.
27
28.
y=hO
Распределение молекул по объему в поле тяготения
Рассмотрим идеальный газ, находящийся в изолированном сосуде в
состоянии термодинамического равновесия в однородном поле тяготения.
Масса всех молекул газа предполагается одинаковой.
В этом случае давление газа будет зависеть от высоты –
координаты y = h .
x
Так как
dp = - r gdh
m M
а плотность r =
=
p Þ
V RT
Mg
dp
Mg
m0 g
dp = pdh Þ
=dh = dh
RT
p
RT
kT
(48)
(49)
28
29.
Проинтегрируем данное уравнение, полагая, чтоh2 > h1
dp
ì
ò p = ln p
ï
m0 g
ï
Þ ln p = ( h2 - h1 )
í h2
kT
ï æ - m0 g ö dh = - m0 g ( h - h )
2
1
ï hò çè kT ÷ø
kT
î1
m0 g
( h2 - h1 )
kT
(50)
2
1
получим:
p = pe
Полученное соотношение называется барометрической формулой.
Если положить h1 = 0 , p1
можно записать в виде
= p0, где p0 - давление на уровне моря, то формулу (50)
p = p0e
m0 gh
kT
(51)
29
30.
Полученные соотношения позволяют исследовать распределение молекулгаза по объему, которое в данном случае не будет равномерным. Используя
уравнение Клапейрона-Менделеева, получим барометрическую формулу для
концентрации молекул газа в любой точке сосуда:
n( x, y , z ) = n0e
где в данном случае
m0 gy
kT
(52)
n0 = n( x,0, z ) = p0 kT
Закон Больцмана
Учитывая, что в данном случае произведение m0 gy равно потенциальной
энергии молекулы Wп в точке с координатами ( x , y , z ), формулу (52) можно
представить в виде:
n ( x, y , z ) = n0e
Wп ( x , y , z )
kT
(53)
30
31.
Закон Больцмана при заданных внешних потенциальных силовых полях позволяет найтираспределение молекул по объему газа.
В соответствии с этим законом число молекул в элементарном объеме dV = dxdydz ,
расположенном в точке с координатами ( x, y , z ), равно
dN ( x, y , z ) = n0e
Wп ( x , y , z )
kT
dxdydz
,
(54)
где концентрация n0 определяется из условия нормировки
n0 òòò e
Wп ( x , y , z )
kT
dxdydz = N
,
(55)
в котором V - объем газа.
V
Распределение (54) называется распределением Больцмана.
6. Распределение Максвелла - Больцмана.
Механическое состояние микрочастицы (молекулы) как материальной точки полностью
характеризуется заданием трех ее координат и трех проекций вектора скорости. Поэтому
каждому такому состоянию может быть соотнесены шесть чисел
{x, y , z,u x ,u y ,u z }
, (56)
31
32.
которые могут рассматриваться как координаты точки в шестимерном пространстве координат и скоростей микрочастицы. Это шестимерное пространство называется фазовымпространством микрочастицы, а набор шести параметров (56) – фазовым состоянием
микрочастицы.
Распределение молекул по фазовым состояниям описывается совокупностью рассмотренных выше распределений Максвелла и Больцмана. Так как координаты и проекции
скоростей суть независимые случайные величины, то их совместное распределение может
быть получено как произведение распределений (29) и (54):
dN ( x, y , z,u x ,u y ,u z ) =
= n0 NА e
3
- b (u x2 +u 2y +u z2 )
e
Wп ( x , y , z )
kT
Обозначая через
W = Wк + Wп = W ( x, y , z ,u x ,u y ,u z ) =
dxdydzdu x du y du z
m0 (u x2 + u y2 + u z2 )
2
+ Wп ( x, y , z )
полную энергию молекулы как материальной точки, запишем распределение (57) в
более компактном виде:
32
(57)
(58)
33.
dN ( x, y , z ,u x ,u y ,u z ) = NBeгде
-
W ( x , y , z ,u x ,u y ,u z )
kT
dxdydzdu x du y du z
3
2
æ m0 ö
B = n0 ç
÷ = const
è 2p kT ø
(59)
(60)
Совместное распределение (59) называется
распределением Максвелла-Больцмана
33
34.
Отметим, что в рассматриваемых моделях молекулярного движения энергия можетпринимать любые значения. В подобных случаях говорят, что микрочастица имеет
непрерывный энергетический спектр.
Вместе с тем, в квантовой физике рассматриваются микрочастицы (в том числе и молекулы), для которых полная энергия может принимать лишь дискретные (квантованные)
значения – т.н. уровни энергии
W1 ,W2 ,...,Wi ,...
(61)
В этом случае говорят, что микрочастица имеет дискретный энергетический спектр.
34
35.
При этом в фазовом пространстве допустимы не все состояния, а только такие, для которых выполняются условия:W = W ( x, y , z,u x ,u y ,u z ) = Wi ,
i = 1, 2,L
(62)
Про микрочастицу, удовлетворяющую условию (62), говорят, что она находится на i-ом
энергетическом уровне. Из общей формы распределения (59) следует, что в этом число
молекул, находящихся на i - м энергетическом уровне, равно
W
N i = NCe
где C - некоторая константа.
Так как
åN
i
i
= NC å e
-
Wi
kT
=N
(64),
i
то
-
i
kT
C = (åe
(63)
-
Wi
kT
)
-1
(65)
Таким образом, распределение (63) можно представить соотношением: i
в котором
N i = Nf МБ ( Wi )
fМБ ( Wi ) = Ce
(66)
-
Wi
kT (67)
Функция fМБ ( Wi ) называется функцией распределения Максвелла-Больцмана
35
для микрочастиц с дискретным энергетическим спектром.
36.
11.5. Статистическое обоснование второго начала термодинамики1. Макроскопические и микроскопические состояния идеального газа.
Статистический вес макросостояния
Рассмотрим идеальный газ, заключенный при отсутствии внешних сил в адиабатическую
оболочку объема V. Пусть в этом объеме содержится 2Nмолекул. Считая все молекулы
различимыми, пронумеруем их от 1 до 2N . Разделим мысленно сосуд с газом на две равные
половины и будем говорить, что газ находится в состоянии A k , если в левой половине находится ровно k молекул, а во второй – 2N - k остальных.
Назовем это состояние макросостоянием газа.
Очевидно, что всего возможны 2N + 1 макросостояний:
Рис.9
A 0 , A 1,..., A k ,..., A 2 N
(68)
Так как молекулы различимы и пронумерованы, то каждое макросостояние может быть
реализовано различными способами в зависимости от того, какие конкретно молекулы
находятся в левой половине сосуда. Каждую такую реализацию будем называть микросостоянием газа. Таким образом, каждому макросостоянию A k соответствует свой
набор реализующих его микросостояний. Число таких микросостояний равно числу
способов выбора k молекул из общего их числа 2N .
36
37.
Это число называется статистическим весом макросостояния и определяетсяформулой:
k = C
k
2N
( 2N )!
=
, k = 0,1,...,2N
k !( 2N - k )!
(69)
2. Статистический вес и вероятность макросостояния. Распределение
вероятностей для макросостояний
Так как в соответствии с гипотезой о характере молекулярного движения все положения
молекул равновероятны, вероятность макросостояния можно представить в виде:
P( A k ) =
k
C k2 N
( 2N )!
= 2N =
, k = 0,1,...,2N
2N
2
k !( 2N - k )!2
2N
å
i=0
(70)
i
Формула (70) характеризует распределение вероятностей для макросостояний.
Анализ показывает, что максимум вероятности (70) достигается при
k=N
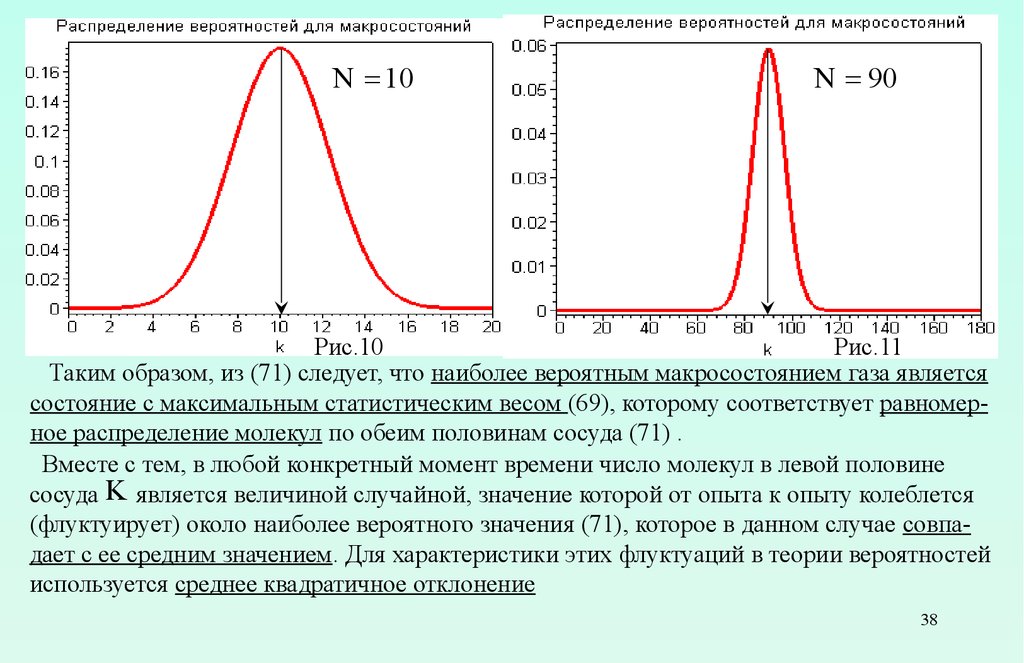
что иллюстрируется графиками функции (70), приведенными на рис.10 и 11.
(71)
37
38.
N = 10N = 90
Рис.10
Рис.11
Таким образом, из (71) следует, что наиболее вероятным макросостоянием газа является
состояние с максимальным статистическим весом (69), которому соответствует равномерное распределение молекул по обеим половинам сосуда (71) .
Вместе с тем, в любой конкретный момент времени число молекул в левой половине
сосуда K является величиной случайной, значение которой от опыта к опыту колеблется
(флуктуирует) около наиболее вероятного значения (71), которое в данном случае совпадает с ее средним значением. Для характеристики этих флуктуаций в теории вероятностей
используется среднее квадратичное отклонение
38
39.
=(K - N )
2
. (72)
Вычисления показывают, что в данном случае среднее квадратичное значение равно половине ширины графика функции распределения (рис.10 и 11) на уровне 0,6 от максимального ее значения и определяется формулой:
N
=
2
а его отношение к общему числу молекул равно
1
=
N
2N
,
(73)
(74)
19
В нормальных условиях в 1 см 3 газа содержится 2N = 2,687 10 молекул. В этом случае отношение (74) равно 1,9 10 -8 » 0,000002% , т.е. пренебрежимо мало. Подсчеты показывают, что для 1 см 3 газа отклонение числа молекул в левой половине сосуда от среднего значения с вероятностью 0,9999999 не превышает величины
0,7 10 -9 N = 0,0000000007 N
Приведенные оценки дают основание считать, что реальные значения числа молекул в
обеих половинах сосуда практически все время одинаковы.
39
40.
3. Статистическое определение энтропии. Вероятностный характервторого начала термодинамики
Знаменитая формула Больцмана определяет энтропию как характеристику макросостояния, связанную с его статистическим весом:
S = S( A k ) = k ln k
(75)
Из определения статистического веса (69) следует, что энтропия может рассматриваться
как мера упорядоченности системы – чем она меньше, тем более упорядочена система
(меньше число микросостояний, реализующих данное макросостояние).
Максимального значения энтропия достигает тогда, когда статистический вес макросостояния максимален – в случае рассмотренного выше примера с газом это соответствует
наиболее вероятному макросостоянию, которому отвечает равномерное распределение
молекул.
Следовательно, при переходе от менее вероятных состояний к более вероятным состояниям энтропия возрастает и, наоборот, рост энтропии свидетельствует о движении системы
в направлении более вероятного макросостояния.
40
41.
Переход системы от одного макросостояния к другому является процессом случайным,при этом теоретически не исключается и переход системы от более вероятного к менее
вероятному макросостоянию, однако на опыте такие переходы не наблюдаются – предоставленная самой себе замкнутая термодинамическая система всегда движется к наиболее
вероятному состоянию и рано или поздно переходит в это состояние, имеющее максимально возможную энтропию и остается в нем сколь угодно долго. Поэтому реальные термодинамические процессы в замкнутой системе всегда сопровождаются либо ростом,
либо постоянством энтропии.
Эти соображения позволяют сформулировать второе начало термодинамики следующим
образом (Больцман, 1877 ):
В любой замкнутой термодинамической системе наиболее
вероятным является процесс, сопровождающийся
неубыванием энтропии.
Отметим в заключение, что вычисление энтропии по формуле (75) дает те же результаты,
что и вычисление ее значения в соответствии с термодинамическим определением (формула (7) темы № 10).
41






































 Физика
Физика








