Похожие презентации:
Уравнение прямой на плоскости
1. Уравнение прямой на плоскости
2. Уравнение прямой, проходящей через две точки
АВ x2 x1 ; y2 y1B(x2; y2)
АМ x x1 ; y y1
M(x; y)
A(x1; y1)
Векторы
АВ и АМ коллинеарны
x x1
y y1
x2 x1 y2 y1
3. Пример
Написать уравнение прямой, проходящей через точки скоординатами А(5; –8) и В(–3; 0)
x 5
y 8
8 x 5 8 y 8
3 5 0 8
x 5 y 8 y x 3
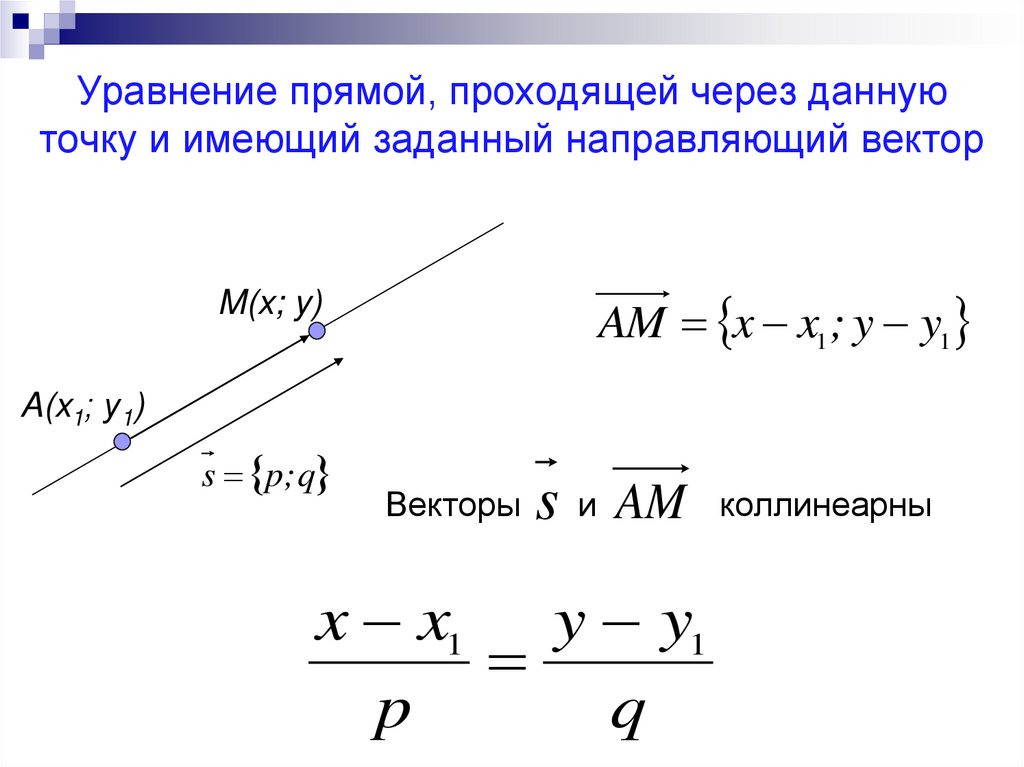
4. Уравнение прямой, проходящей через данную точку и имеющий заданный направляющий вектор
AM x x1 ; y y1M(x; y)
A(x1; у1)
s p; q
Векторы
s и AM
x x1 y y1
p
q
коллинеарны
5. Пример
Написать уравнение прямой, проходящей через точку скоординатами А(5; 5) и имеющей направляющий вектор
s = (9; 10)
x 5 y 5
10( x 5 ) 9( y 5 )
9
10
10 x 50 9 y 45 9 y 10 x 5
10
5
y x
9
9
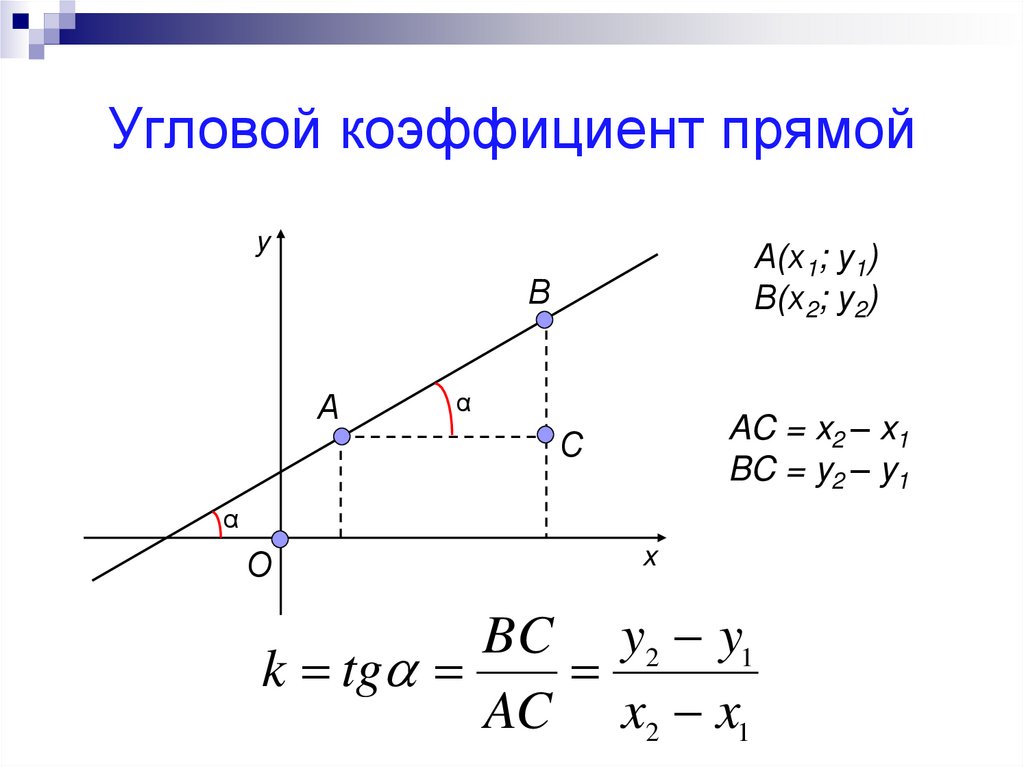
6. Угловой коэффициент прямой
yА(х1; у1)
В(х2; у2)
В
А
α
AC = x2 – x1
BC = y2 – y1
С
α
О
x
BC y2 y1
k tg
AC x2 x1
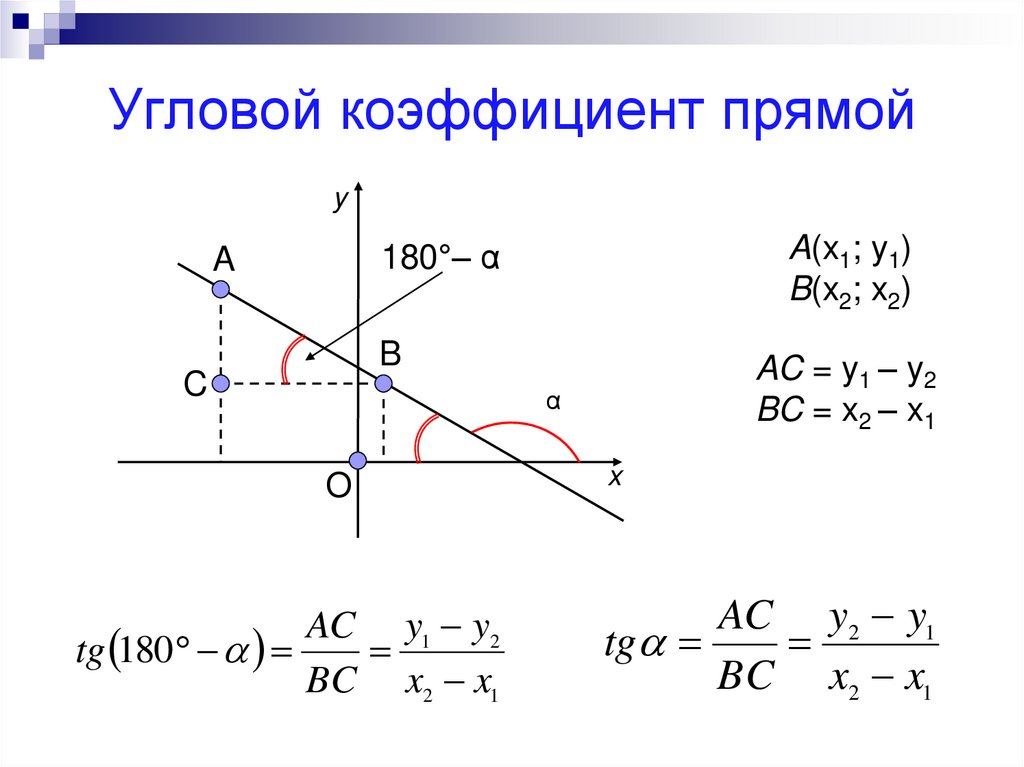
7. Угловой коэффициент прямой
yA(x1; y1)
B(x2; x2)
180°– α
A
B
C
AC = y1 – y2
BC = x2 – x1
α
O
AC y1 y2
tg 180
BC x2 x1
x
AC y2 y1
tg
BC x2 x1
8. Пример
Найти угловой коэффициент прямой, проходящейчерез точки с координатами A(-1; 4) и B(5; 8)
8 4 4 2
k
5 1 6 3
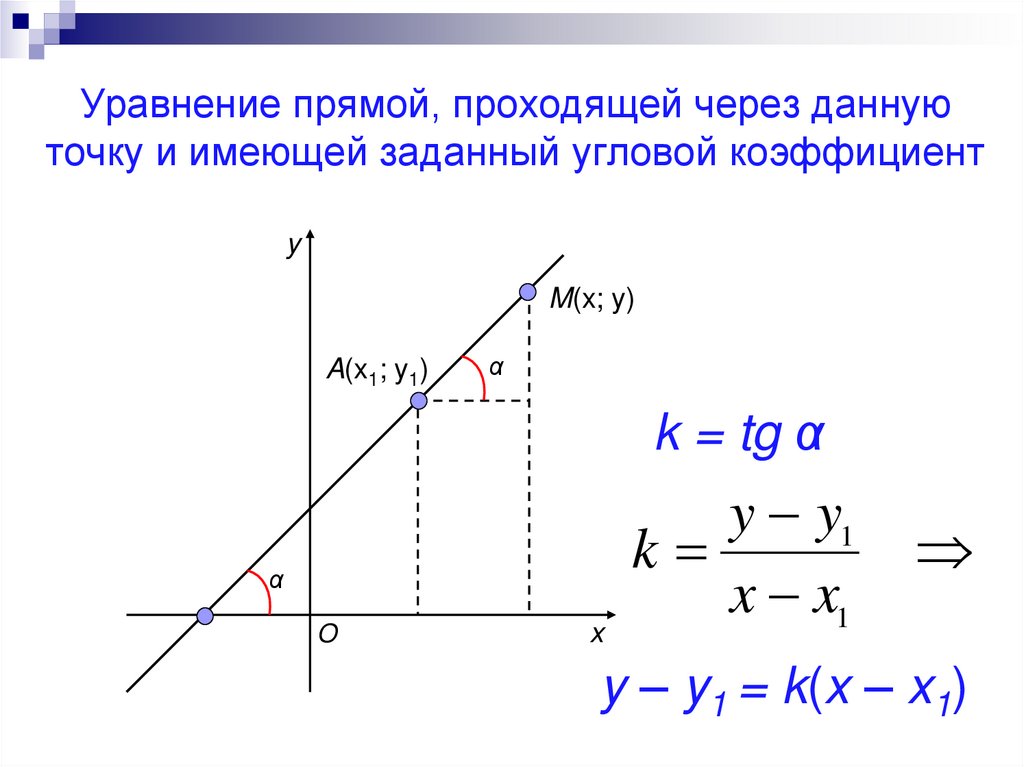
9. Уравнение прямой, проходящей через данную точку и имеющей заданный угловой коэффициент
yM(x; y)
A(x1; y1)
α
k = tg α
α
O
x
y y1
k
x x1
y – y1 = k(x – x1)
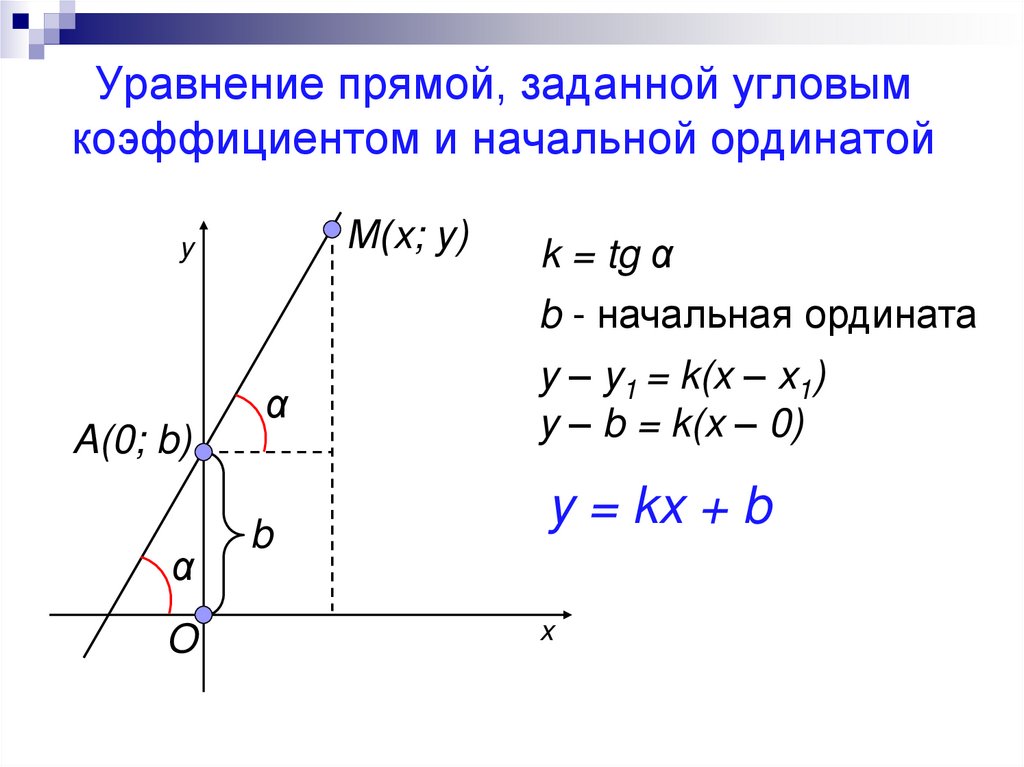
10. Уравнение прямой, заданной угловым коэффициентом и начальной ординатой
М(x; y)y
k = tg α
b - начальная ордината
A(0; b)
α
O
α
b
y – y1 = k(x – x1)
y – b = k(x – 0)
y = kx + b
x
11. Общее уравнение прямой
y = kx + b 0 = kx – y + bkx – y + b = 0
A = k;
B = -1;
C=b
Ax + By + c = 0 где, А ≠ 0 или В ≠ 0
12. Линейное уравнение
Ax + Bx + C = 0, в котором хотя бы одиниз коэффициентов А или В отличен от
нуля, называется общим уравнением
прямой







 Математика
Математика








