Похожие презентации:
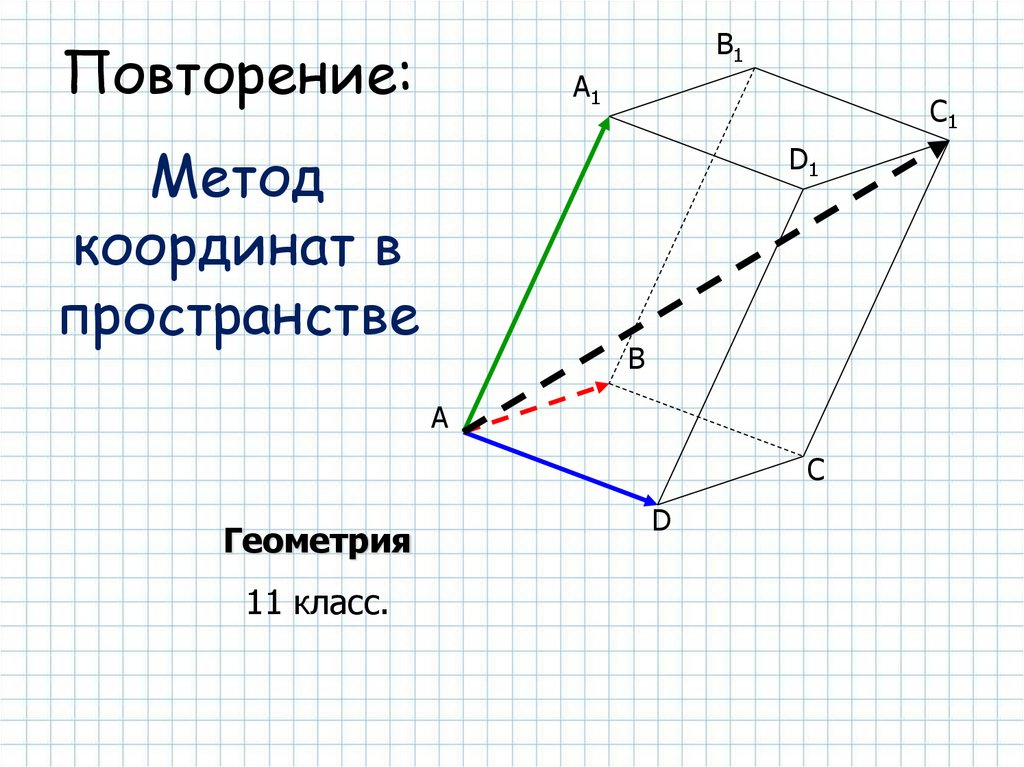
Метод координат в пространстве
1.
B1Повторение:
A1
Метод
координат в
пространстве
C1
D1
B
A
C
Геометрия
11 класс.
D
2. Цели урока:
1.Повторить понятия вектора;2.Повторить понятие прямоугольной
системы координат в пространстве.
Задачи урока:
-вспомнить умения строить точку по
заданным её координатам и находить
координаты точки, изображённой в
заданной системе координат,
-решить задачи ЕГЭ
3. Содержание урока:
Повторение понятия вектора;
Прямоугольная система координат;
Понятия координат векторов;
Решение задач координатным
методом;
4.
Определение вектора.Как и в плоскости, в пространстве вектор определяется как направленный
отрезок:
B
A
Точка А – начало вектора, В – конец вектора. Записывают:
AB
или
a.
Вектор, у которого начало совпадает с конечной точкой называется нулевым,
обозначается: 0 или AA .
0
Длина отрезка, изображающего вектор, называется модулем вектора, т.е.
AB AB åä.î ò ð. .
5.
Если через точкупространства
проведены три попарно
перпендикулярные
прямые, на каждой из них
выбрано направление и
выбрана единица
измерения отрезков, то
говорят, что
задана система
координат в
пространстве.
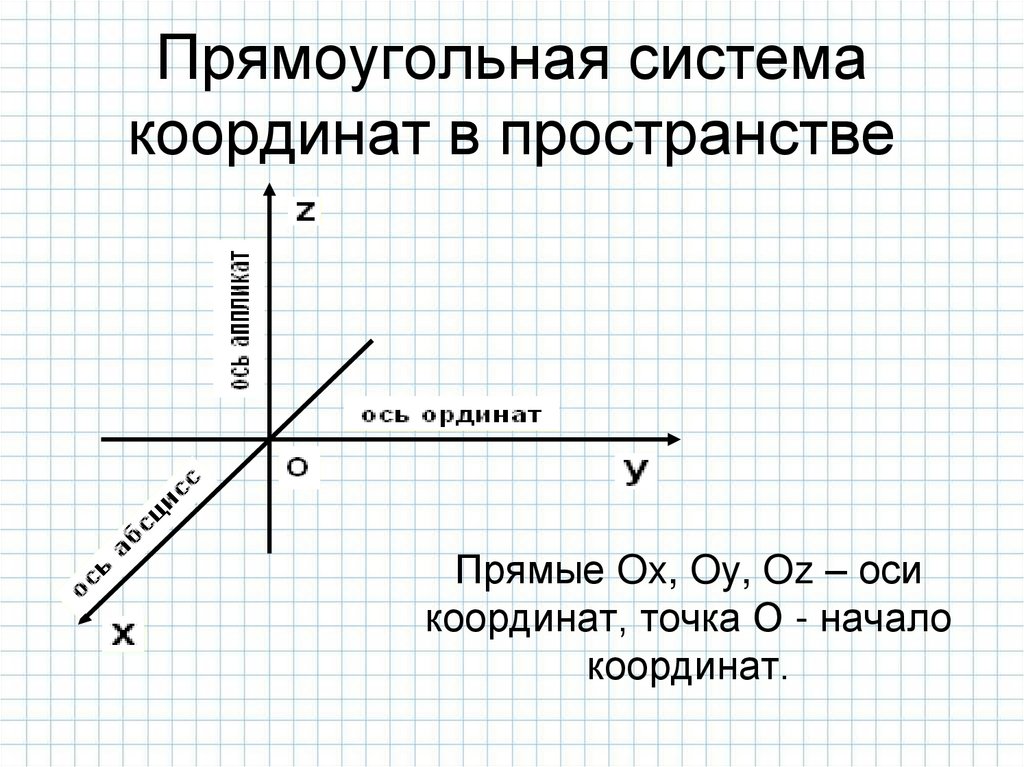
6. Прямоугольная система координат в пространстве
Прямые Ox, Oy, Oz – осикоординат, точка О - начало
координат.
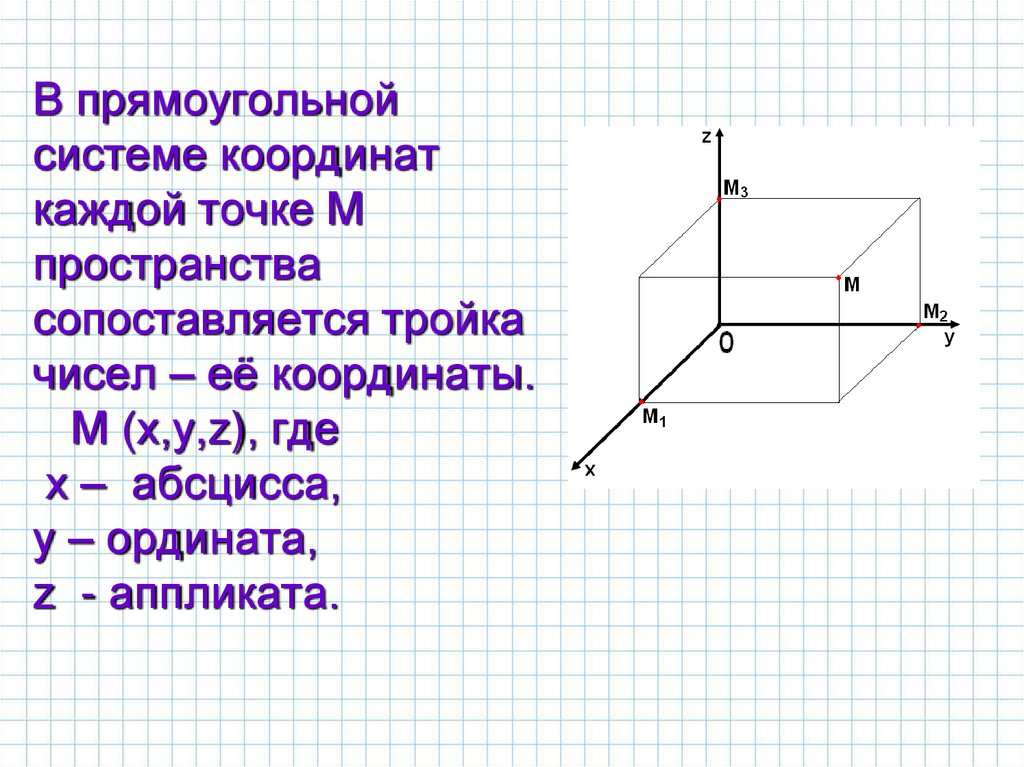
7. В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел – её координаты. М (х,у,z), где х –
абсцисса,у – ордината,
z - аппликата.
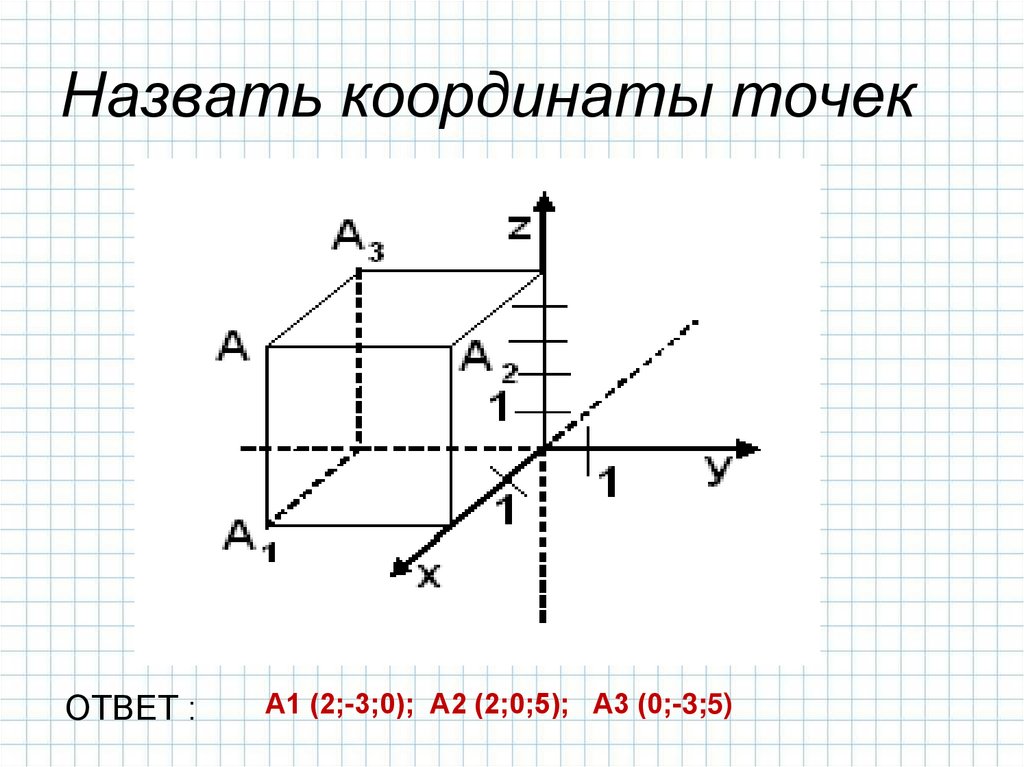
8. Назвать координаты точек
ОТВЕТ :А1 (2;-3;0); А2 (2;0;5); А3 (0;-3;5)
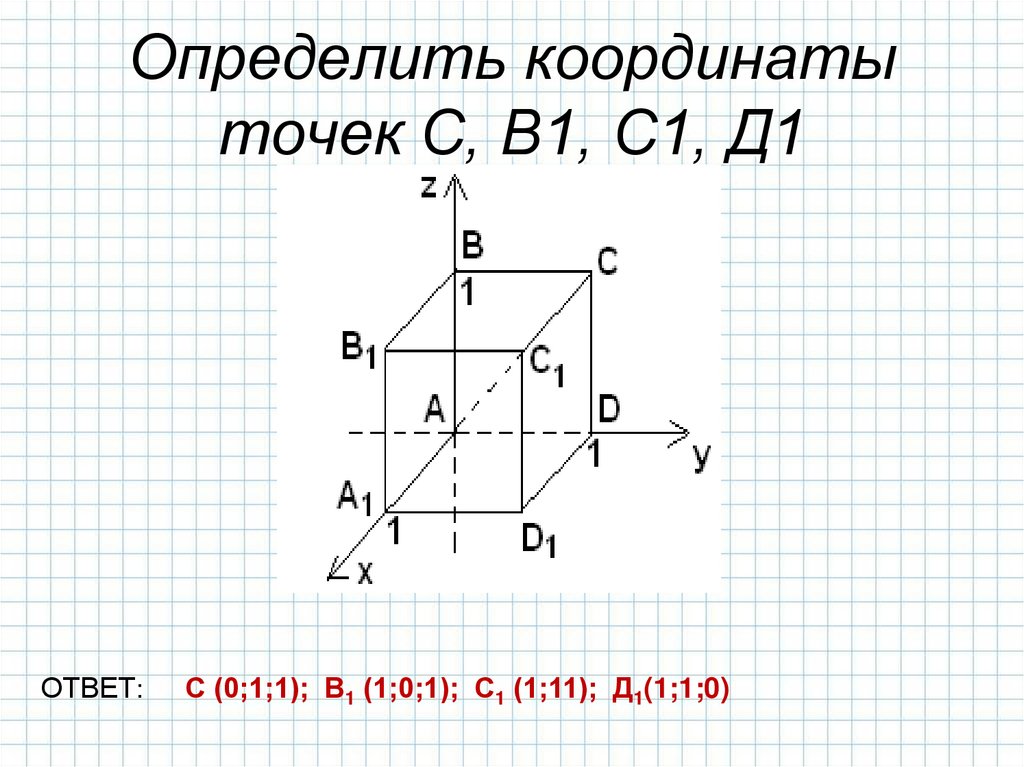
9. Определить координаты точек С, В1, С1, Д1
ОТВЕТ:С (0;1;1); В1 (1;0;1); С1 (1;11); Д1(1;1;0)
10. Координаты вектора. - Вспомнить метод координат. -Вспомнить понятие единичных векторов; - Рассмотреть правила сложения,
вычитания,умножения;
- Решение задач.
11.
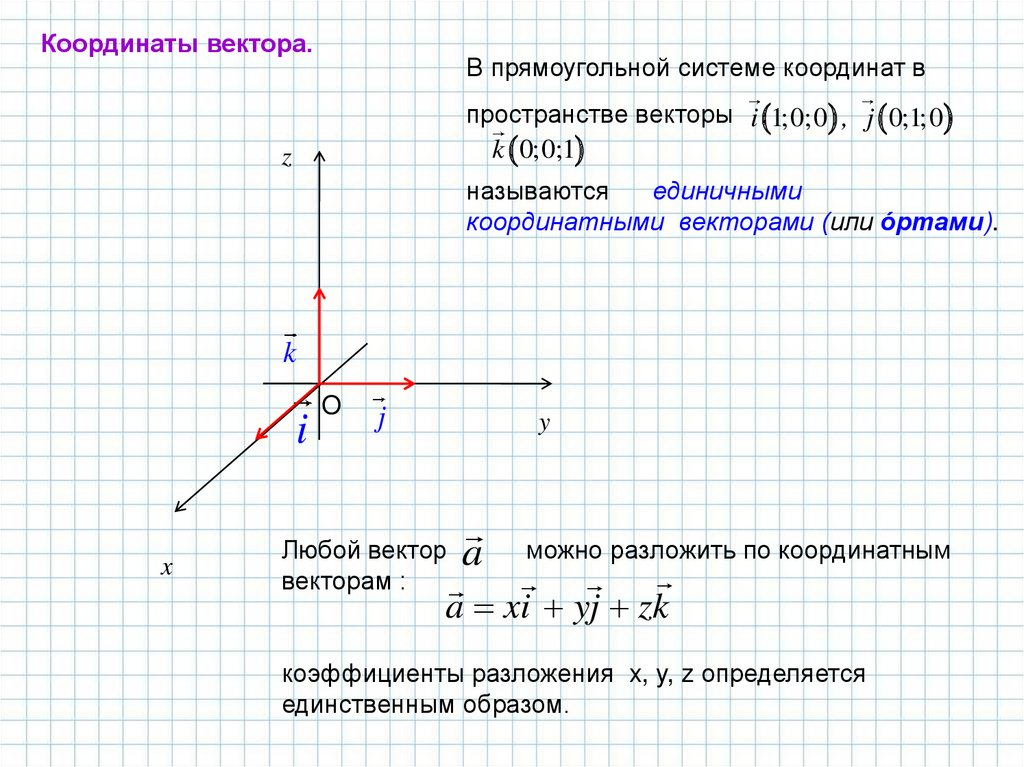
Координаты вектора.В прямоугольной системе координат в
пространстве векторы i 1;0;0 , j 0;1;0
k 0;0;1
z
называются
единичными
координатными векторами (или óртами).
k
i
x
O
j
y
a
Любой вектор
векторам :
можно разложить по координатным
a xi yj zk
коэффициенты разложения x, y, z определяется
единственным образом.
12.
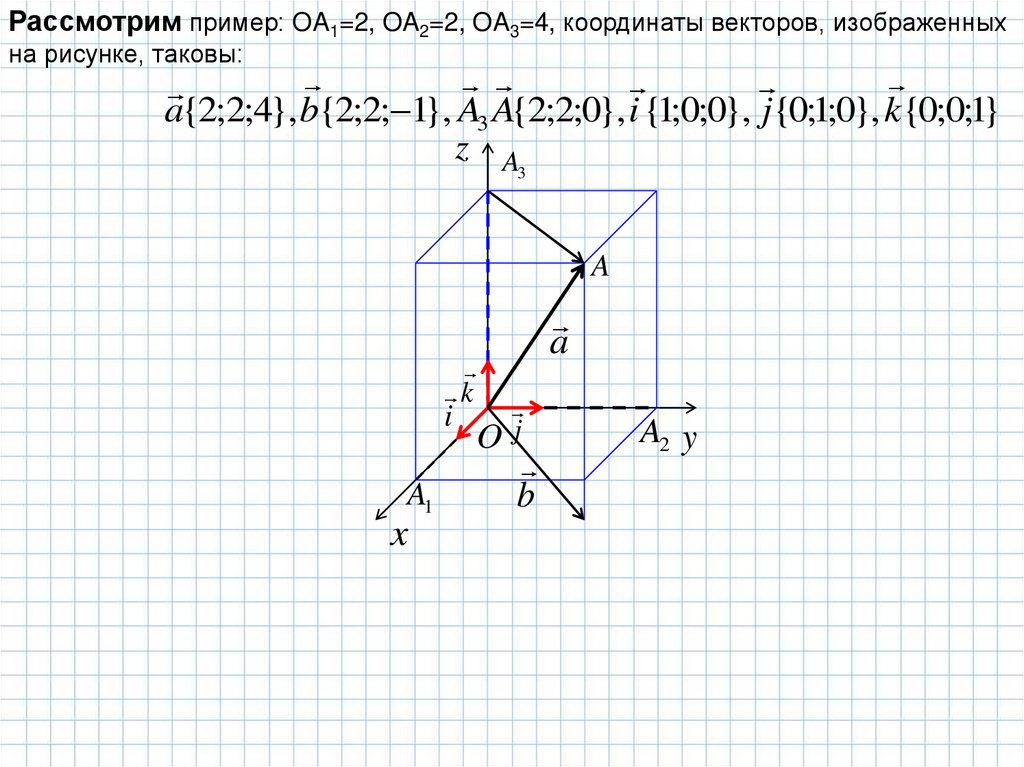
Рассмотрим пример: OA1=2, OA2=2, OA3=4, координаты векторов, изображенныхна рисунке, таковы:
a{2;2;4}, b{2;2; 1}, A3 A{2;2;0}, i {1;0;0}, j{0;1;0}, k {0;0;1}
z A
3
A
k
i
A1
x
O
a
j
b
A2 y
13.
a{x1 , y1 , z1}b { x2 , y 2 , z 2 }
10. Каждая координата суммы 2х или более векторов равна сумме
соответствующих координат этих векторов, т.е.
{x1 x2 ; y1 y2 ; z1 z2}
20. Каждая координата разности 2х векторов равна разности
соответствующих координат этих векторов, т.е.
{x1 x2 ; y1 y2 ; z1 z2}
30. Каждая координата произведения вектора на число
равна
произведению соответствующей координаты вектора на это число.
{ x, y, z}
14. Задача
Даны векторы: a{3; 5;2}, b{0;7; 1}, c{2 / 3;0;0}, d { 2.7;3.1;0.5}Найти координаты векторов:
d a
Решение:
a c
1. a b ;
2. a{3; 5;2} И b{0;7; 1}
3. a b {3 0; 5 7;2 ( 1)} {3;2;1}
Ответ:
a b {3;2;1}
b c
15. Самостоятельная работа
Вариант 2Даны векторы: a{ 1;2;0}, b{0; 5; 2}, c{2;1; 3}
Вариант 1
Найти координаты
векторов:
p 3b 2a c
p a 2c 4b
Найти координаты
векторов:
q 3c 2b a
q 7c 2b 6a
16.
Задание 14 № 526703ЕГЭ
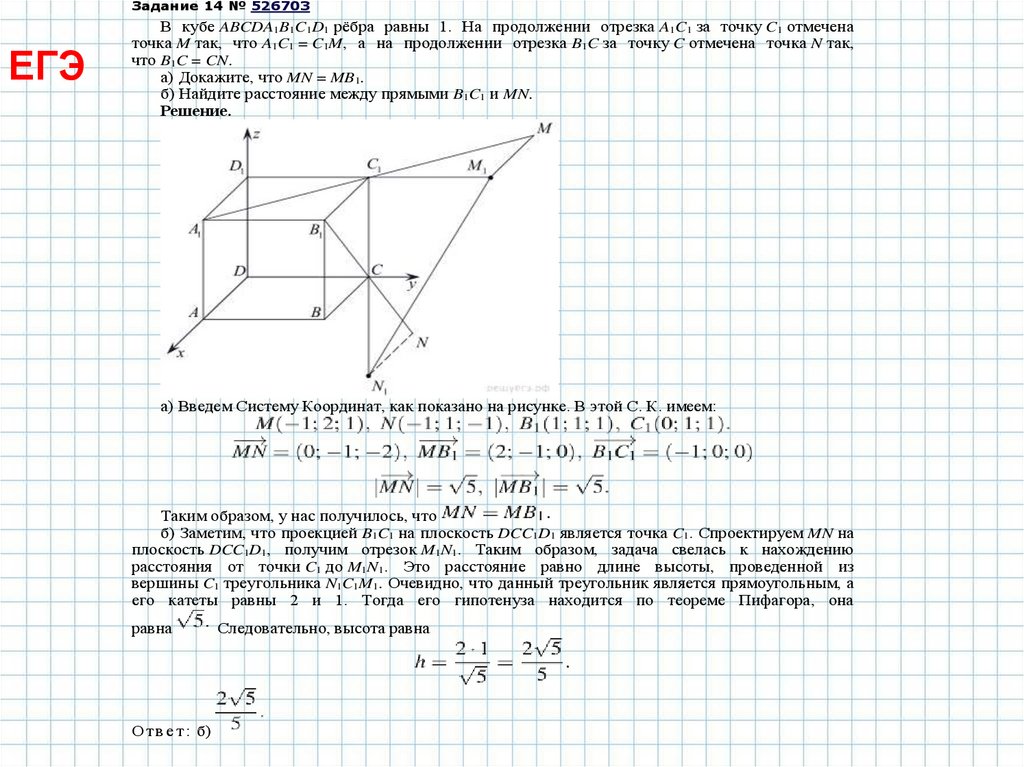
В кубе ABCDA1B1C1D1 рёбра равны 1. На продолжении отрезка A1C1 за точку C1 отмечена
точка M так, что A1C1 = C1M, а на продолжении отрезка B1C за точку C отмечена точка N так,
что B1C = CN.
а) Докажите, что MN = MB1.
б) Найдите расстояние между прямыми B1C1 и MN.
Решение.
а) Введем Систему Координат, как показано на рисунке. В этой С. К. имеем:
Таким образом, у нас получилось, что
б) Заметим, что проекцией B1C1 на плоскость DCC1D1 является точка C1. Спроектируем MN на
плоскость DCC1D1, получим отрезок M1N1. Таким образом, задача свелась к нахождению
расстояния от точки C1 до M1N1. Это расстояние равно длине высоты, проведенной из
вершины C1 треугольника N1C1M1. Очевидно, что данный треугольник является прямоугольным, а
его катеты равны 2 и 1. Тогда его гипотенуза находится по теореме Пифагора, она
равна
О т в е т : б)
Следовательно, высота равна








 Математика
Математика