Метод координат в пространстве. Урок № 4

1.

МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
Урок № 4
План урока:
1 Устно повторим материал предыдущего
урока.
2 Напишем СР.
3 Узнаем о нахождении координат вектора
в пространстве.
4 Изучим простейшие задачи в
координатах.
5 Порешаем задачи.
6 Запишем ДЗ.

2.

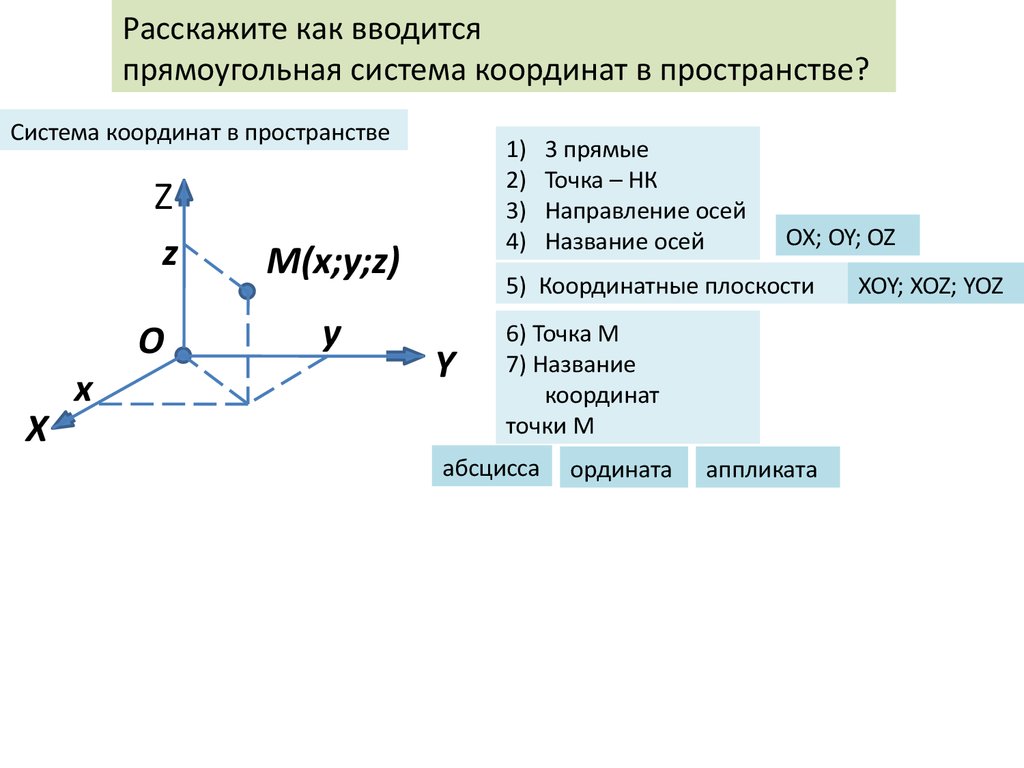
Расскажите как вводится
прямоугольная система координат в пространстве?
Система координат в пространстве
Z
z
X
x
О
1)
2)
3)
4)
M(x;y;z)
y
3 прямые
Точка – НК
Направление осей
Название осей
OX; OY; OZ
5) Координатные плоскости
Y
6) Точка М
7) Название
координат
точки М
абсцисса
ордината
аппликата
XOY; XOZ; YOZ

3.

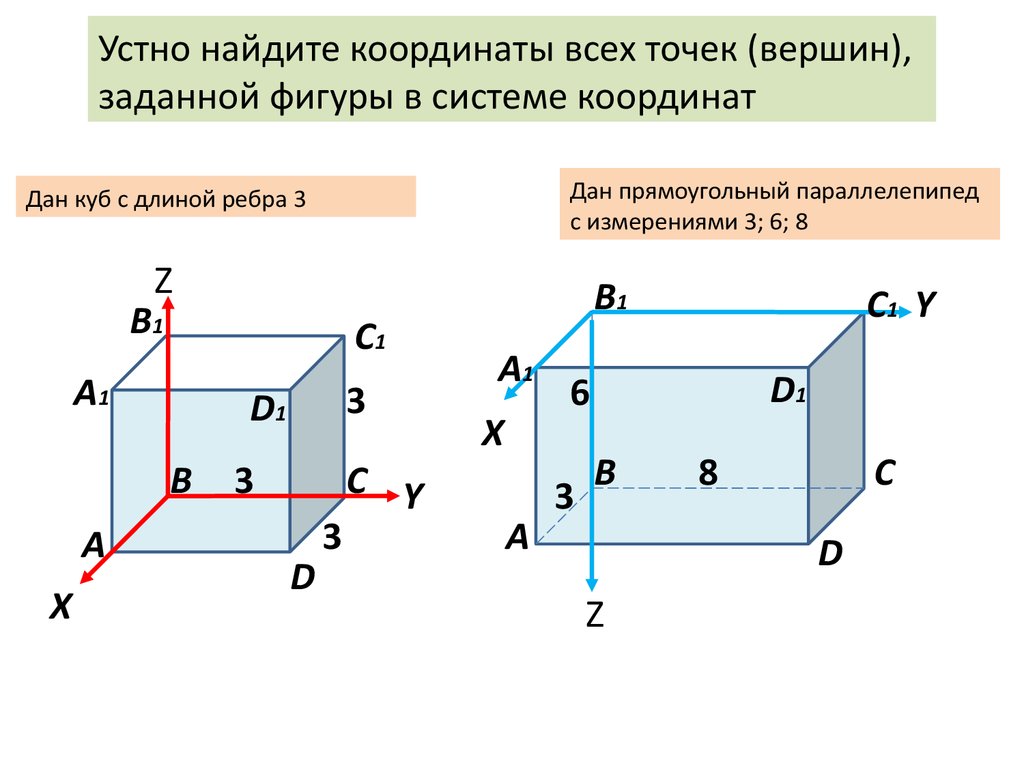
Устно найдите координаты всех точек (вершин),
заданной фигуры в системе координат
Дан прямоугольный параллелепипед
с измерениями 3; 6; 8
Дан куб с длиной ребра 3
Z
B1
C1
A1
B
A
X
3
D1
3
D
3
C Y
B1
A1
X
A
C1 Y
D1
6
3
B
8
C
D
Z

4.

М ( x; y; z )
Z
М
k
О
j
i
X
i {1; 0;0}
j{0;1 ;0}
k {0;0;1}
Y
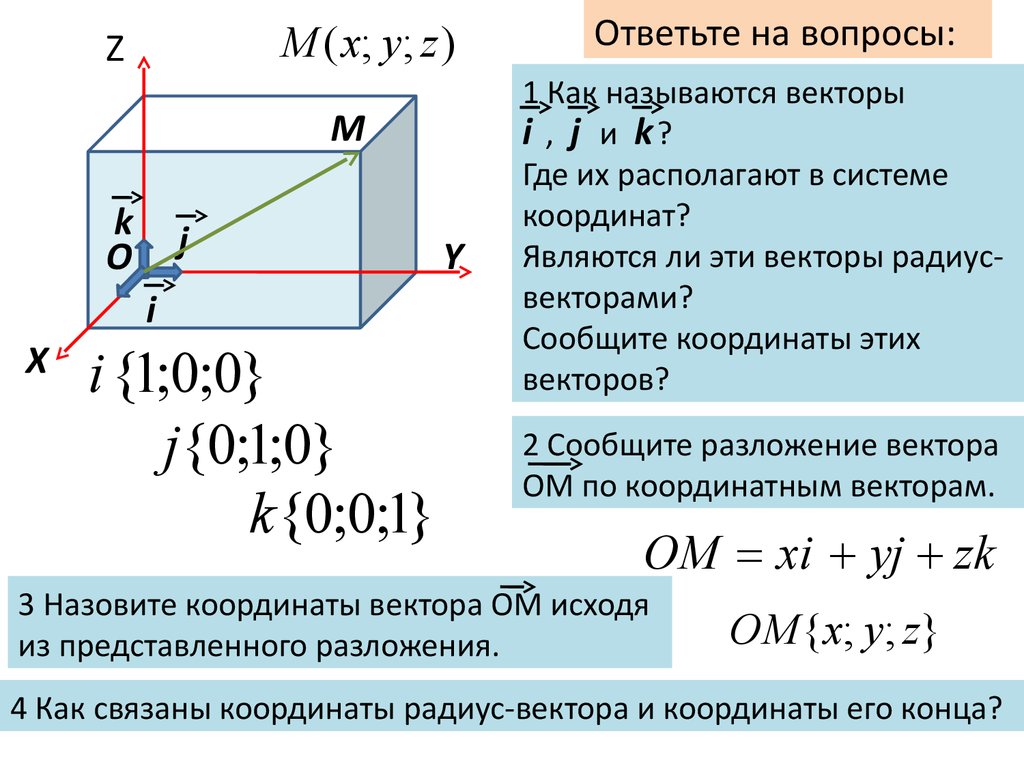
Ответьте на вопросы:
1 Как называются векторы
i , j и k?
Где их располагают в системе
координат?
Являются ли эти векторы радиусвекторами?
Сообщите координаты этих
векторов?
2 Сообщите разложение вектора
ОМ по координатным векторам.
ОМ xi yj zk
3 Назовите координаты вектора ОМ исходя
из представленного разложения.
ОМ {x; y; z}
4 Как связаны координаты радиус-вектора и координаты его конца?

5.

Расскажите о нахождении координат векторов
суммы, разности, вектора умноженного на число?
Координаты
разности векторов,
суммы векторов,
(a+b){ },
a{x1;y1;z1}
(a-b){ },
вектора, умноженного на число
b{x2;y2;z2}
ka{ }
Сообщите план нахождения координат вектора
1
p 0,1a b
2
если
a{5; 10;20}
b{16; 24;8}

6.

Сообщите координаты вектора,
зная его разложение по единичным координатным векторам:
a 7i 5 j 6k
ОМ xi yj zk
b 2j k
c i
ОМ {x; y; z}
Сообщите разложение вектора
по единичным координатным векторам, если:
a{ 2;4; 6}
b{0;5;0}
c{ 3;0; 1}
СР на 8 мин по простейшим задачам в пространстве

7.

Координаты вектора
M(x;y;z)
Z
радиус-вектор
M(x;y;z)
О
Y
ОM{x;y;z}
1 Как называется вектор
начало которого
совпадает с началом
координат?
2 Какая связь между координатами радиус-вектора
и координатами точки, которая является его
концом?
Z
X
3 Сообщите словами правило нахождения
координат вектора, зная координаты его
начала и конца.
X
B(x2;y2;z2)
A(x1;y1;z1)
О
Y
AB{x2-x1;y2-y1;z2-z1}
Чтобы найти координаты вектора, нужно из
соответствующей координаты конца вектора
вычесть соответствующую координату начала

8.

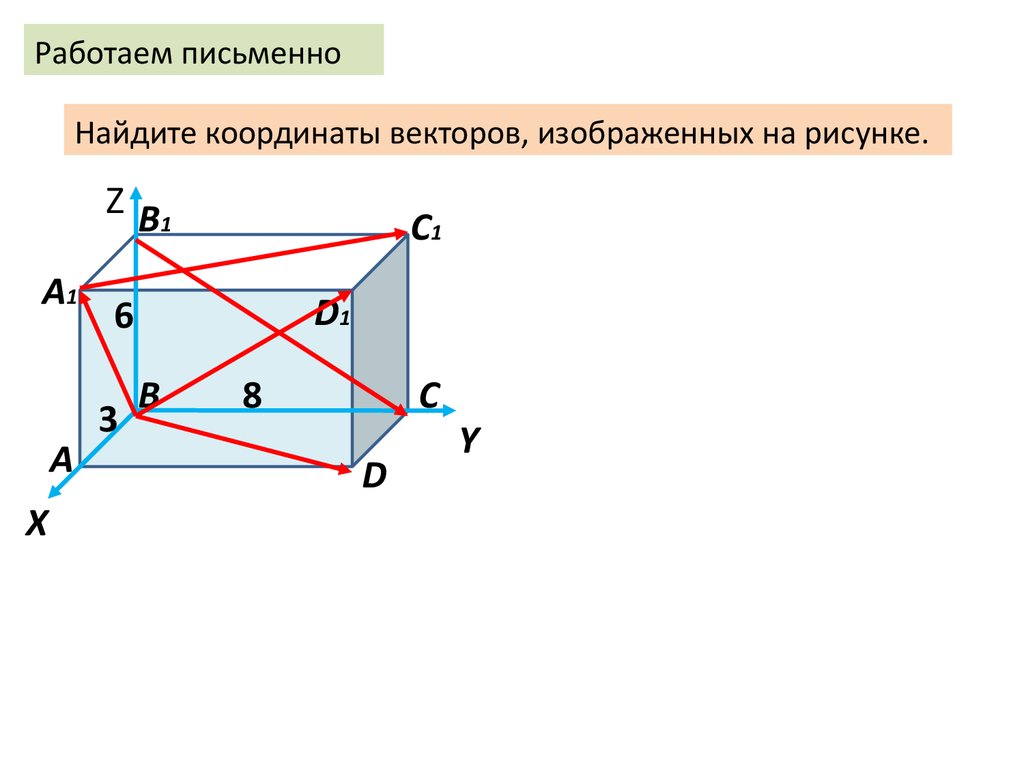
Работаем письменно
Найдите координаты векторов, изображенных на рисунке.
Z B1
A1
A
X
C1
D1
6
3
B
8
C
D
Y

9.

2) Длина вектора
Простейшие задачи в координатах
1) Координаты середины отрезка
C(x;y;z)
A(x1;y1;z1)
x1 x2
x
,
2
a{x;y;z}
a x2 y2 z 2
B(x2;y2;z2)
Координаты середины отрезка полусуммы одноименных координат
y1 y2
y
,
2
z1 z 2
z
2
Длина вектора –
корень квадратный
из суммы
квадратов
координат
3) Расстояние между двумя точками
B(x2;y2;z2)
A(x1;y1;z1)
Длина отрезка – корень квадратный из
суммы квадратов разностей одноименных
координат
AB ( x2 x1 ) ( y2 y1 ) ( z 2 z1 )
2
2
2

10.

Поработаем письменно

11.

12.

Домашнее задание с урока 4:
п.48, 49 и конспект, уметь составить грамотный рассказ,
№ по ситуации задач решенных в классе.