Похожие презентации:
Теорема о трех перпендикулярах
1. Уважаемые обучающиеся! Задание на 21.05.2020 Тема : ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ ПЛАН ЗАНЯТИЯ: 1) Рядом с темой пишем фамилию
и готовуюработу высылаем в лс.
2) Решить задачи 1 и 2 (по предыдущей теме)
3) Записать конспект по теме (слайды 5,6,7)
4) Решить задачу 3 (по готовому плану
решения)
2. ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ
3.
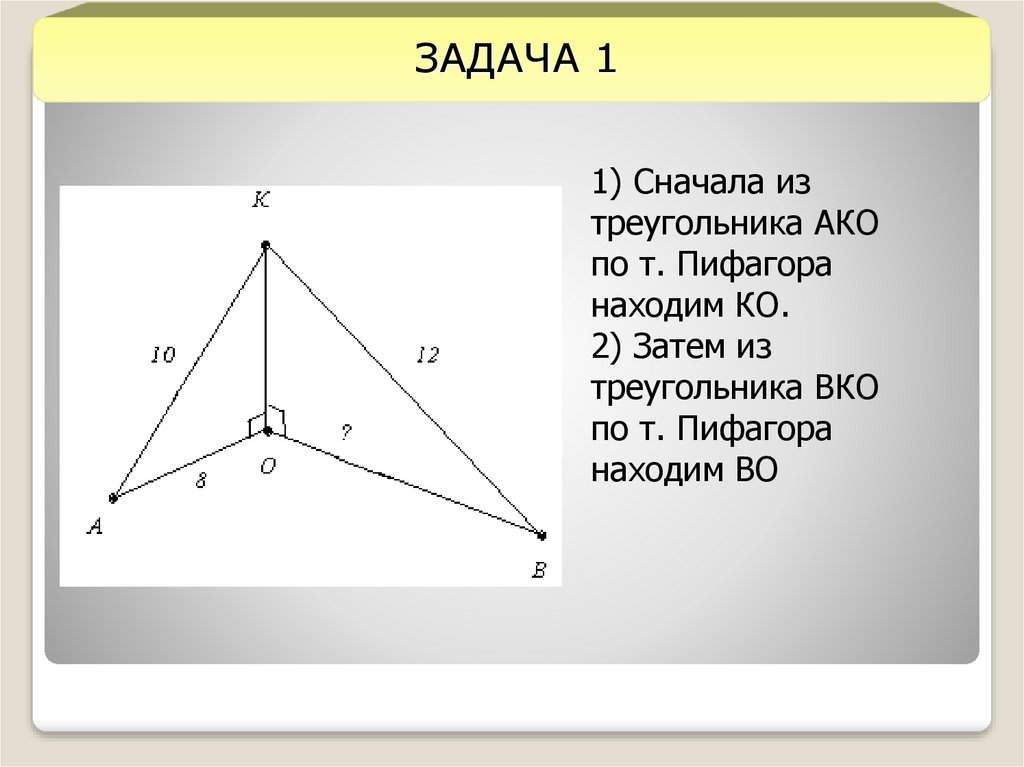
ЗАДАЧА 11) Сначала из
треугольника АКО
по т. Пифагора
находим КО.
2) Затем из
треугольника ВКО
по т. Пифагора
находим ВО
4.
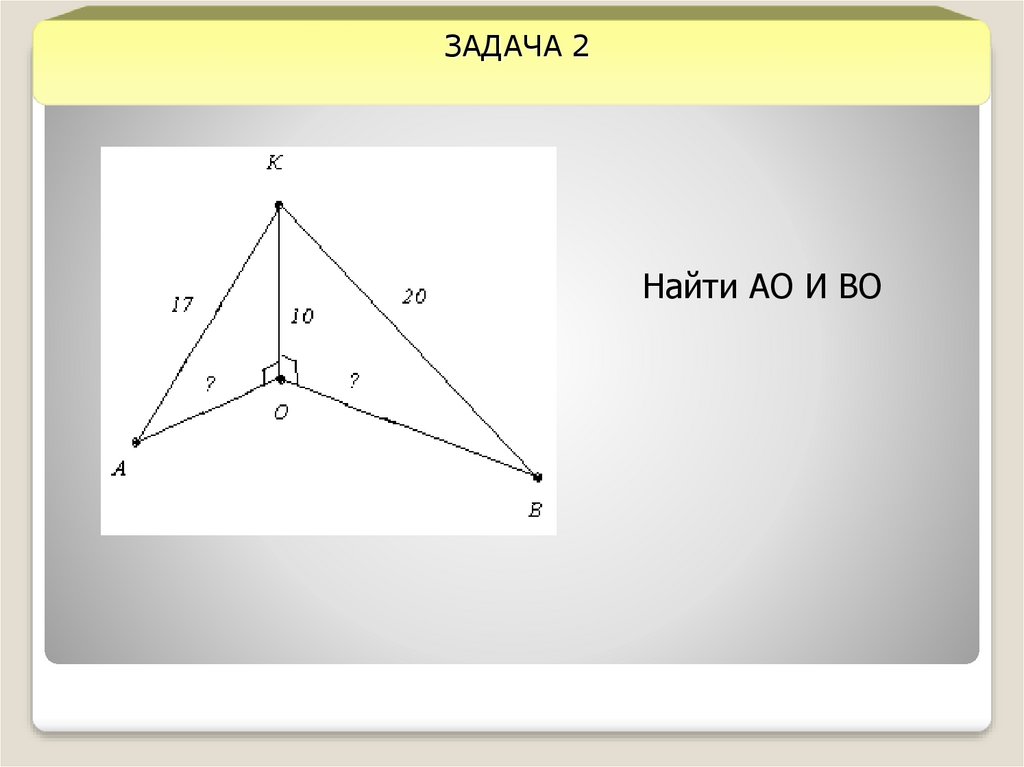
ЗАДАЧА 2Найти АО И ВО
5.
ТЕОРЕМА О ТРЕХПЕРПЕНДИКУЛЯРАХ
Если прямая, проведенная на
плоскости через основание
наклонной, перпендикулярна ее
проекции, то она перпендикулярна
наклонной.
6.
AA'
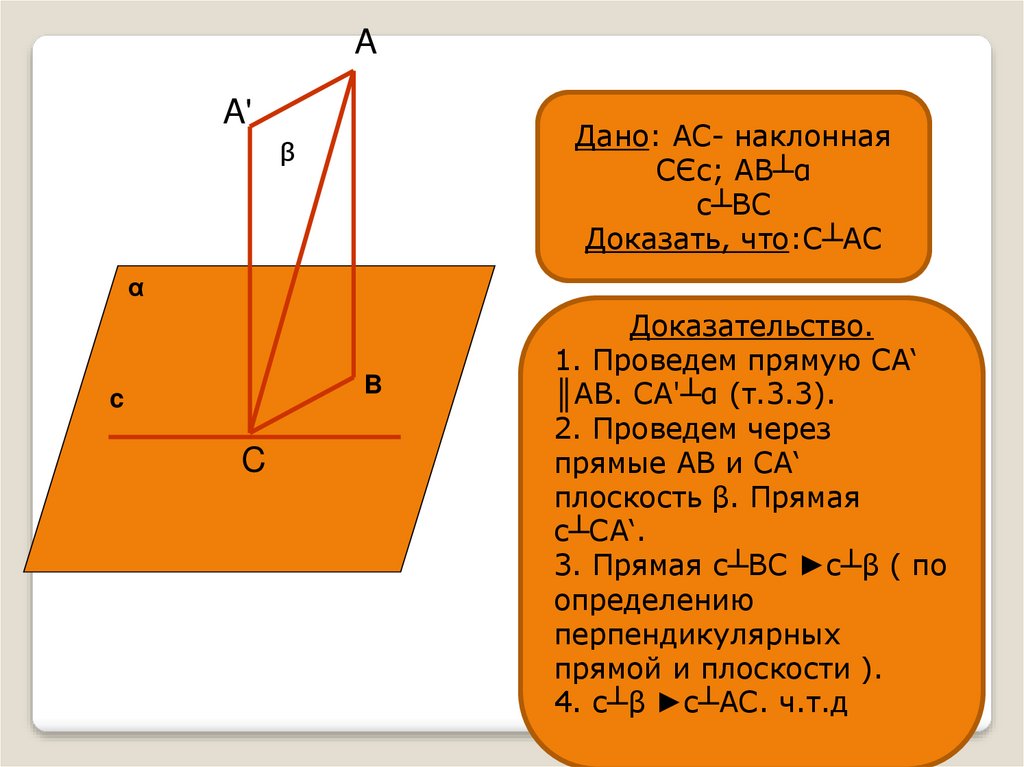
Дано: AC- наклонная
СЄс; AB┴α
c┴BC
Доказать, что:C┴AC
β
α
B
c
C
Доказательство.
1. Проведем прямую СА‘
║АВ. СА'┴α (т.3.3).
2. Проведем через
прямые АВ и СА‘
плоскость β. Прямая
с┴СА‘.
3. Прямая с┴ВС ►с┴β ( по
определению
перпендикулярных
прямой и плоскости ).
4. с┴β ►с┴АС. ч.т.д
7.
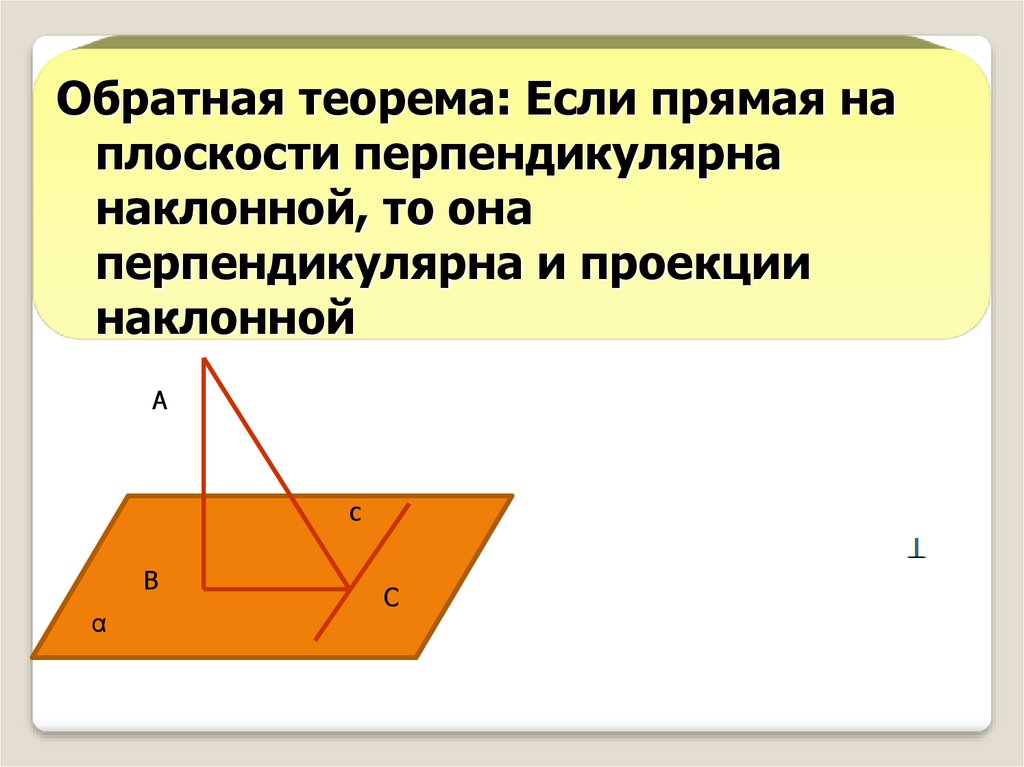
Обратная теорема: Если прямая наплоскости перпендикулярна
наклонной, то она
перпендикулярна и проекции
наклонной
А
А
с
В
α
С
8.
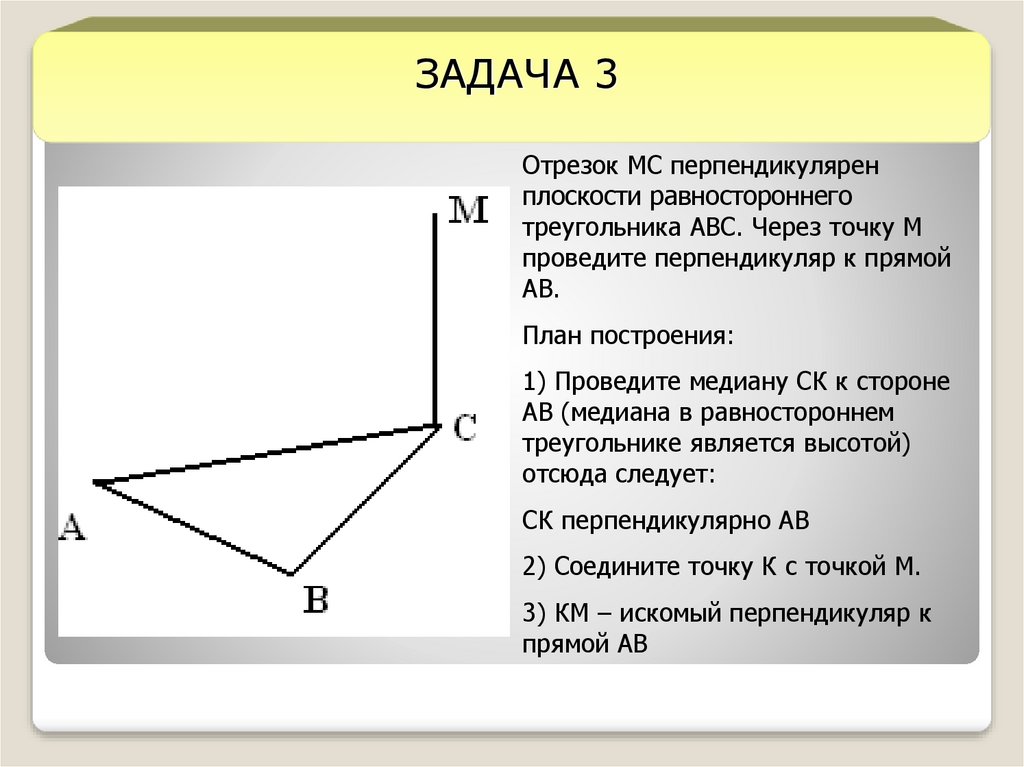
ЗАДАЧА 3Отрезок МС перпендикулярен
плоскости равностороннего
треугольника АВС. Через точку М
проведите перпендикуляр к прямой
АВ.
План построения:
1) Проведите медиану СК к стороне
АВ (медиана в равностороннем
треугольнике является высотой)
отсюда следует:
СК перпендикулярно АВ
2) Соедините точку К с точкой М.
3) КМ – искомый перпендикуляр к
прямой АВ



 Математика
Математика








