Теорема о трех перпендикулярах

1.

Центр образования « Школа здоровья» № 1099 « Ярославский».
п
е
р
п
е
н
д
и
к
у
л
я
р
А
Сенникова Н. В.
учитель
математики
С
В
m
Учебник Л. С.
Атанасян и др.
«Геометрия 10-11»
г. Москва

2.

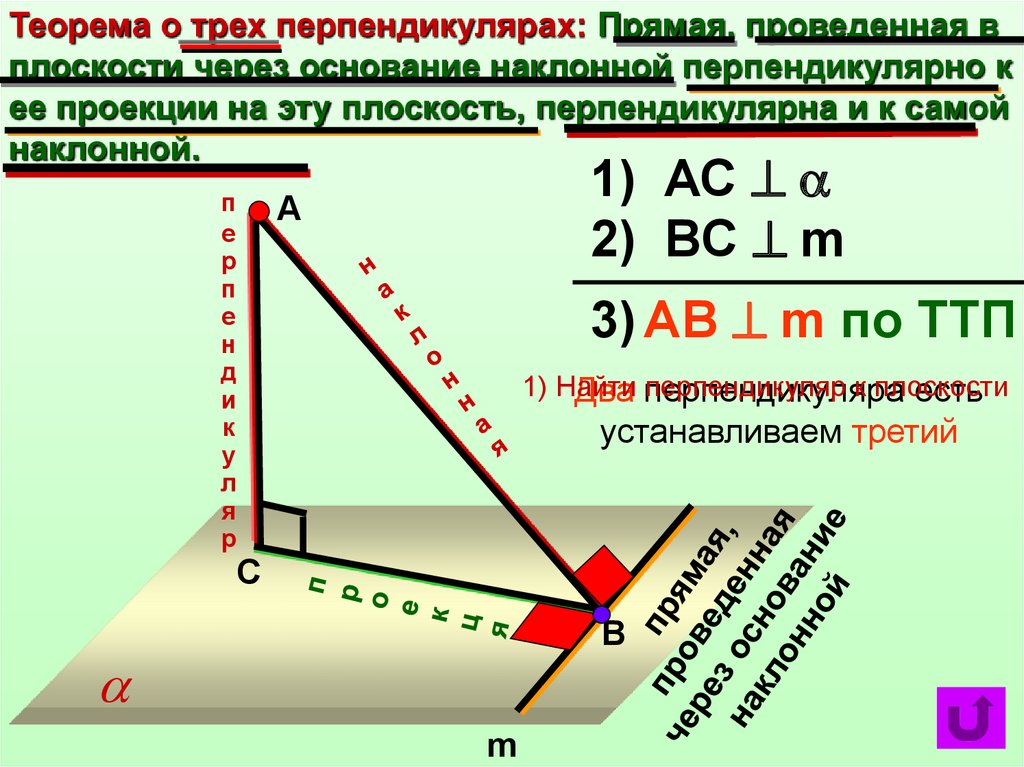
Теорема о трех перпендикулярах: Прямая, проведенная в
плоскости через основание наклонной перпендикулярно к
ее проекции на эту плоскость, перпендикулярна и к самой
наклонной.
п
е
р
п
е
н
д
и
к
у
л
я
р
1) АС
2) BС m
А
3) АB m по ТТП
1) Найти
перпендикуляр к плоскости
Два перпендикуляра
есть
устанавливаем третий
С
В
m

3.

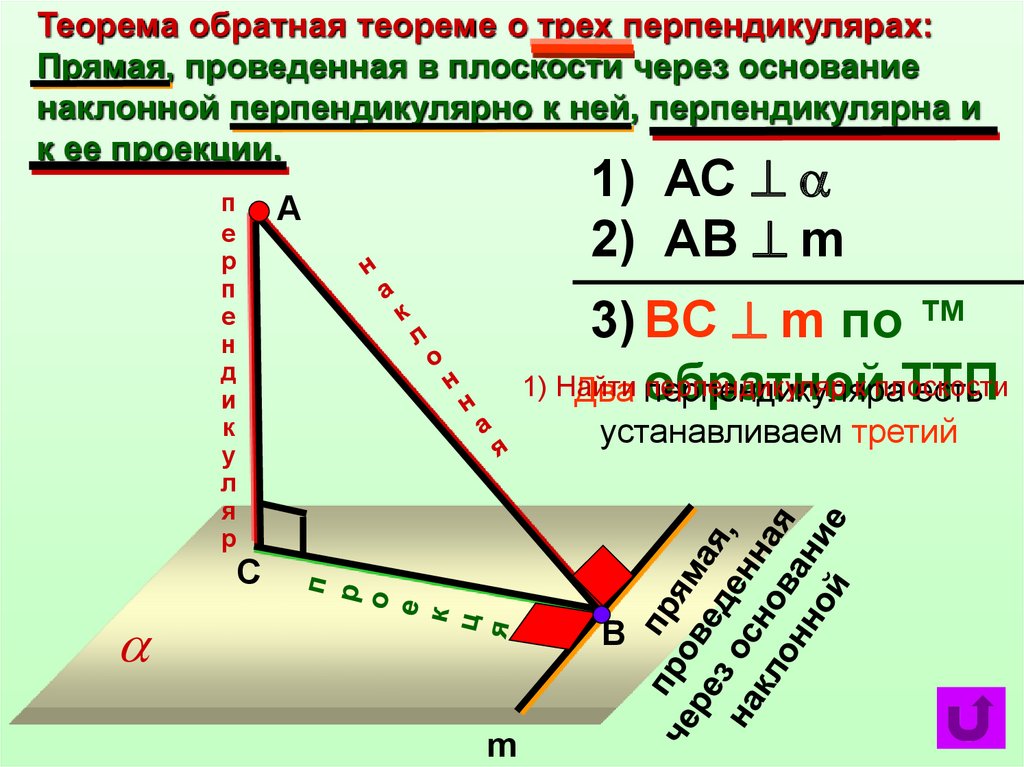
Теорема обратная теореме о трех перпендикулярах:
Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ней, перпендикулярна и
к ее проекции.
п
е
р
п
е
н
д
и
к
у
л
я
р
1) АС
2) АB m
А
3) BС m по ™
1) Найти
перпендикуляр к плоскости
ТТП
Два обратной
перпендикуляра
есть
устанавливаем третий
С
В
m

4.

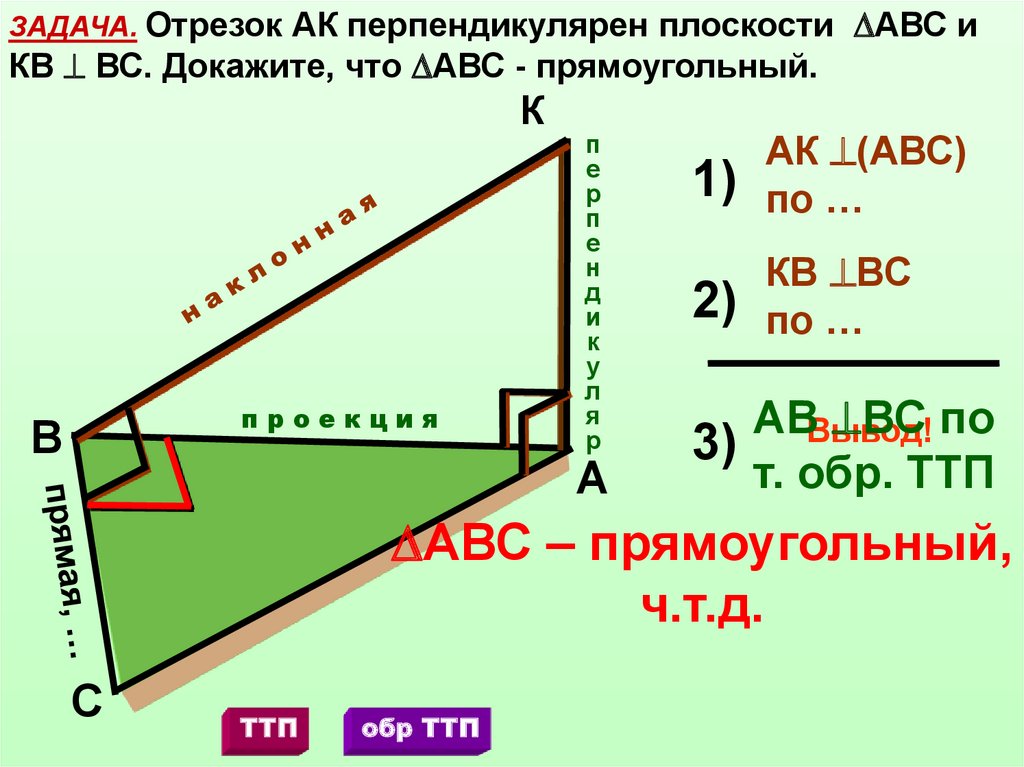
ЗАДАЧА. Отрезок АК перпендикулярен плоскости АВС и
КВ ВС. Докажите, что АВС - прямоугольный.
К
проекция
В
п
е
р
п
е
н
д
и
к
у
л
я
р
А
1)
АК (АВС)
по …
2)
КВ ВС
по …
АВВывод!
ВС по
3)
т. обр. ТТП
АВС – прямоугольный,
ч.т.д.
С
ТТП
обр ТТП

5.

Изобразите отрезок, длина которого равна расстоянию от
т. М до выделенной прямой. Ответ обоснуйте.
С
п
е
р
п
е
н
д
и
к
у
л
я
р
Читаем чертеж!
М
Анализируем дано!
СМ (АВС) по …
СВ АВ по …
Строим расстояние!
проекция
В
Делаем вывод!
D
ТТП
А
обр ТТП
МВ АВ по ТТП
МВ – искомое расстояние

6.

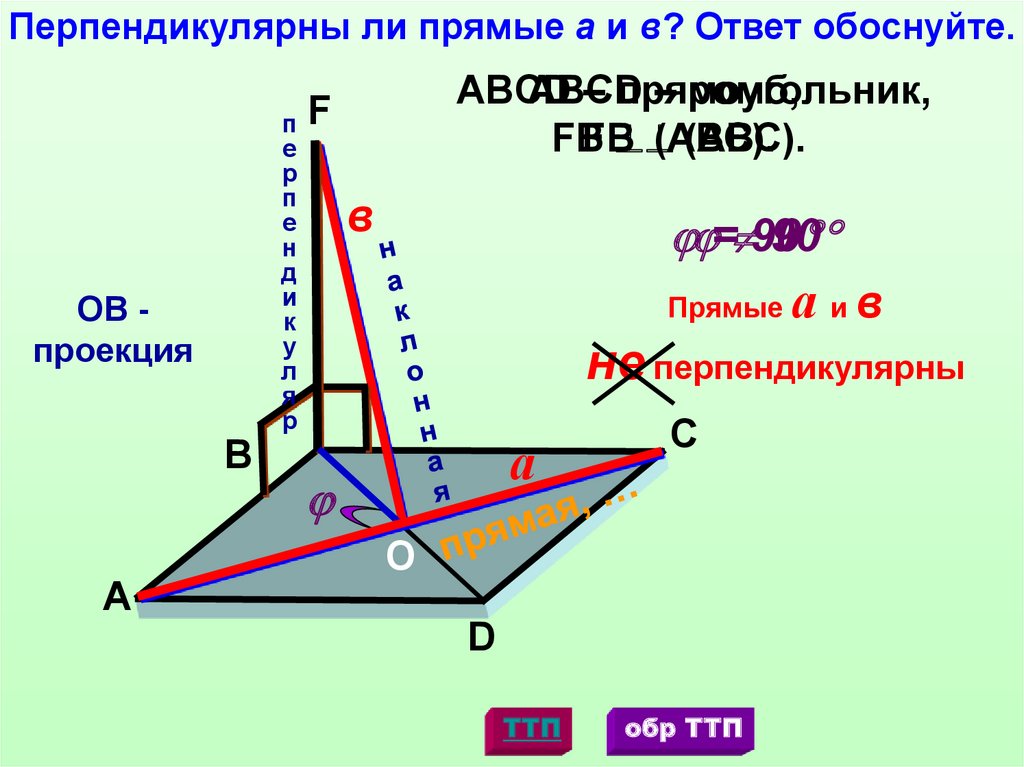
Перпендикулярны ли прямые а и в? Ответ обоснуйте.
ОВ проекция
В
А
п
е
р
п
е
н
д
и
к
у
л
я
р
ABCD
ABCD
– прямоугольник,
– ромб,
FB
FB (АВС).
(АВС).
F
в
= 90
90
Прямые
а ив
не перпендикулярны
а
С
О
D
ТТП
обр ТТП

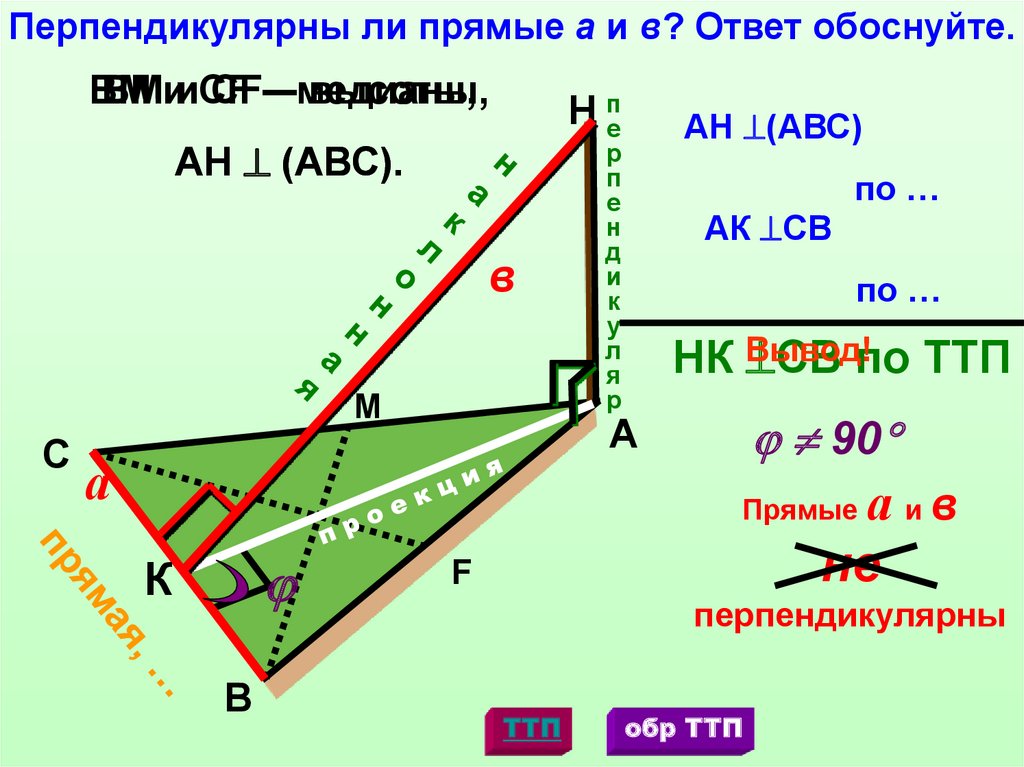
7.

Перпендикулярны ли прямые а и в? Ответ обоснуйте.
BM
BMииCF
CF––медианы,
высоты,
H пе
AH (АВС).
в
M
С
р
п
е
н
д
и
к
у
л
я
р
АН (АВС)
АК СВ
по …
НК Вывод!
СВ по ТТП
90
А
а
по …
а ив
не
Прямые
К
F
К
В
перпендикулярны
ТТП
обр ТТП

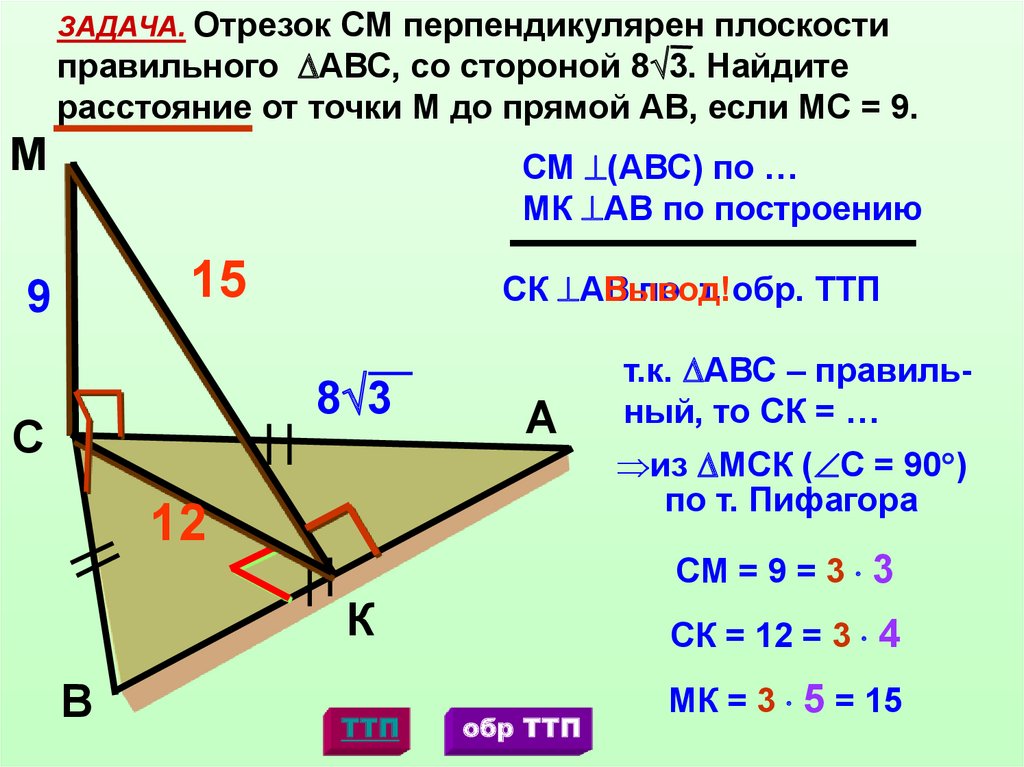
8.

ЗАДАЧА. Отрезок СМ перпендикулярен плоскости
правильного АВС, со стороной 8 3. Найдите
расстояние от точки М до прямой АВ, если МС = 9.
М
СМ (АВС) по …
МК АВ по построению
15
9
СК АВ
Вывод!
по т. обр. ТТП
8 3
С
А
12
из МСК ( С = 90 )
по т. Пифагора
СМ = 9 = 3 3
К
В
т.к. АВС – правильный, то СК = …
ТТП
СК = 12 = 3 4
обр ТТП
МК = 3 5 = 15

9.

ЗАДАЧА. К центру квадрата АВСD восстановлен перпенди-
куляр ОК, равный 5. Найдите расстояние от точки К до
стороны квадрата, если она равна 24.
ОК (АВС) по …
МК АВ по построению
K
Вывод!
ОМ АВ по т. обр. ТТП
5
O
13
C
B
24
O
D
12
A
М
A
М
B

10.

ЗАДАЧА. Отрезок ВМ перпендикулярен плоскости АВС,
где С = 90 , АВ = 17, АС = 8. Найдите расстояние от точки
М до прямой АС, если МВ = 20.
Дано: АВС, С = 90 , АВ = 17,
М
АС = 8, ВМ (АВС).
25
20
Найти: Расстояние от т. М до АС.
Решение:
МК АС по построению
ВМ (АВС) по …
ВК АСВывод!
по т. обр. ТТП
В
15
17
С
НО ВС АС, что …
т.К совпадает с т. С и
искомое расстояние МС
8
К
А
ЗАКОНЧИТЬ
САМОСТОЯТЕЛЬНО

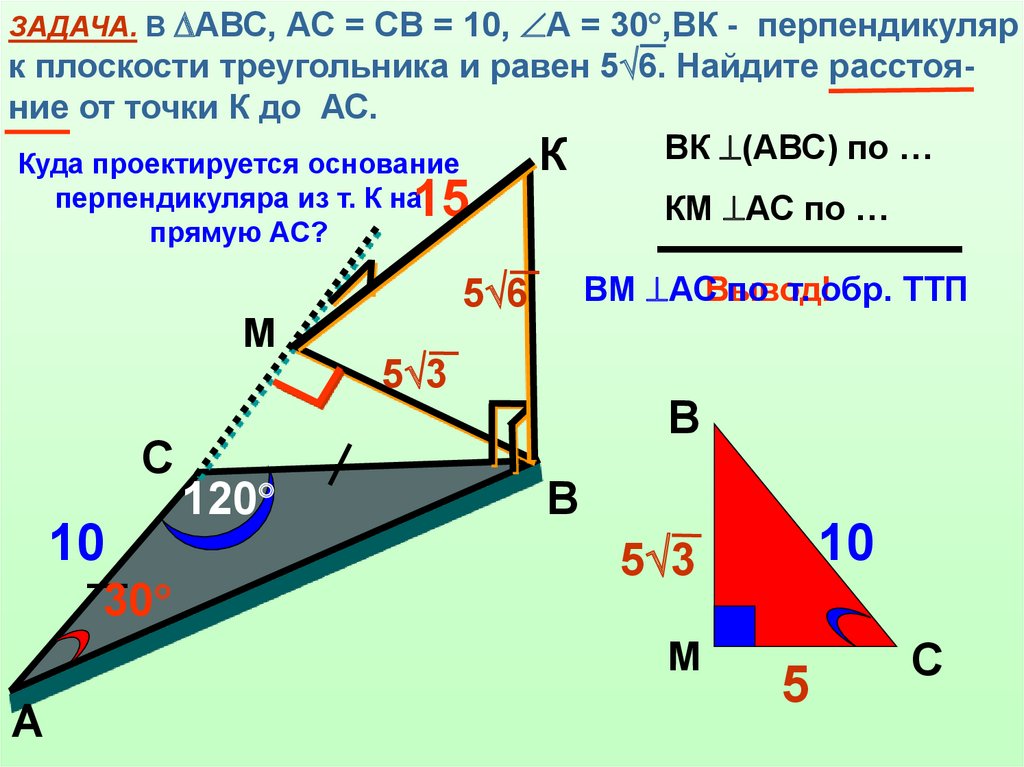
11.

ЗАДАЧА. В АВС, АС = СВ = 10, А = 30 ,ВК - перпендикуляр
к плоскости треугольника и равен 5 6. Найдите расстояние от точки К до АС.
ВК (АВС) по …
К
Куда проектируется основание
15
перпендикуляра из т. К на
прямую АС?
КМ АС по …
ВМ АСВывод!
по т. обр. ТТП
5 6
М
5 3
С
10
30
120
В
В
М
А
10
5 3
5
С

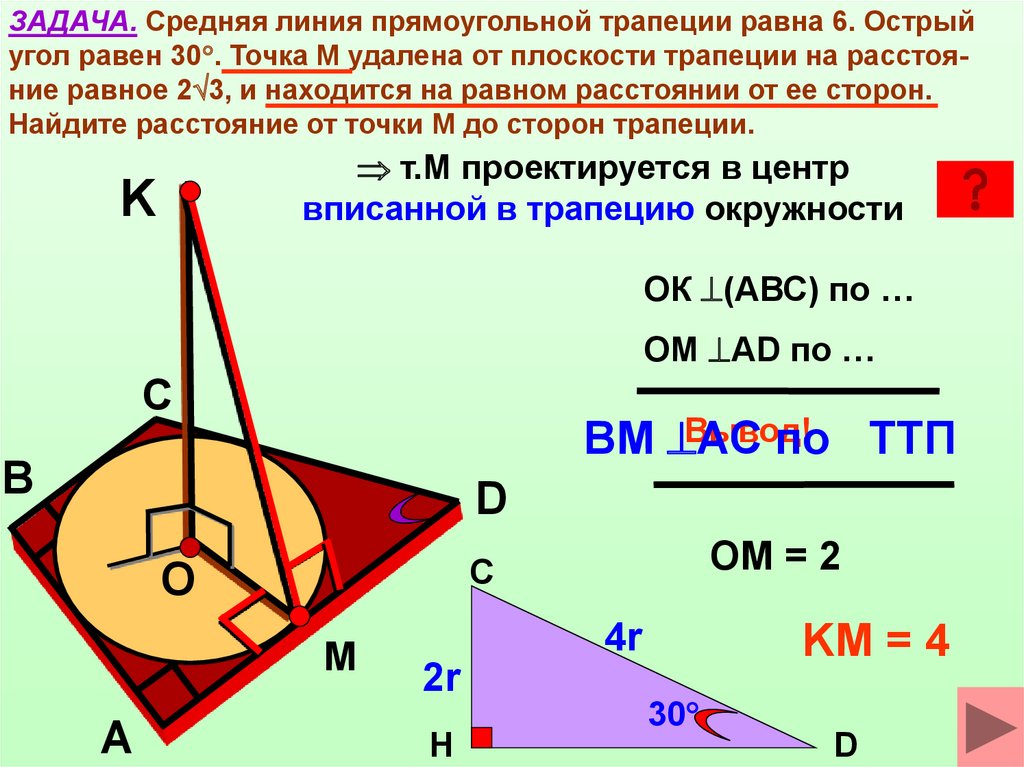
12.

ЗАДАЧА. Средняя линия прямоугольной трапеции равна 6. Острый
угол равен 30 . Точка М удалена от плоскости трапеции на расстояние равное 2 3, и находится на равном расстоянии от ее сторон.
Найдите расстояние от точки М до сторон трапеции.
т.М проектируется в центр
вписанной в трапецию окружности
K
ОК (АВС) по …
ОМ АD по …
С
Вывод!
ВМ АС
по ТТП
B
D
O
М
A
OM = 2
C
4r
KM = 4
2r
H
30
D

13.

ЗАДАЧА. Средняя линия прямоугольной трапеции равна 6. Острый
угол равен 30 . Точка М удалена от плоскости трапеции на расстояние равное 2 3, и находится на равном расстоянии от ее сторон.
Найдите расстояние от точки М до сторон трапеции.
т.М проектируется в центр
вписанной в трапецию окружности
в+е+ р+а
в
в
=
в+е +р +а
е
е
а
а
р
р

14.

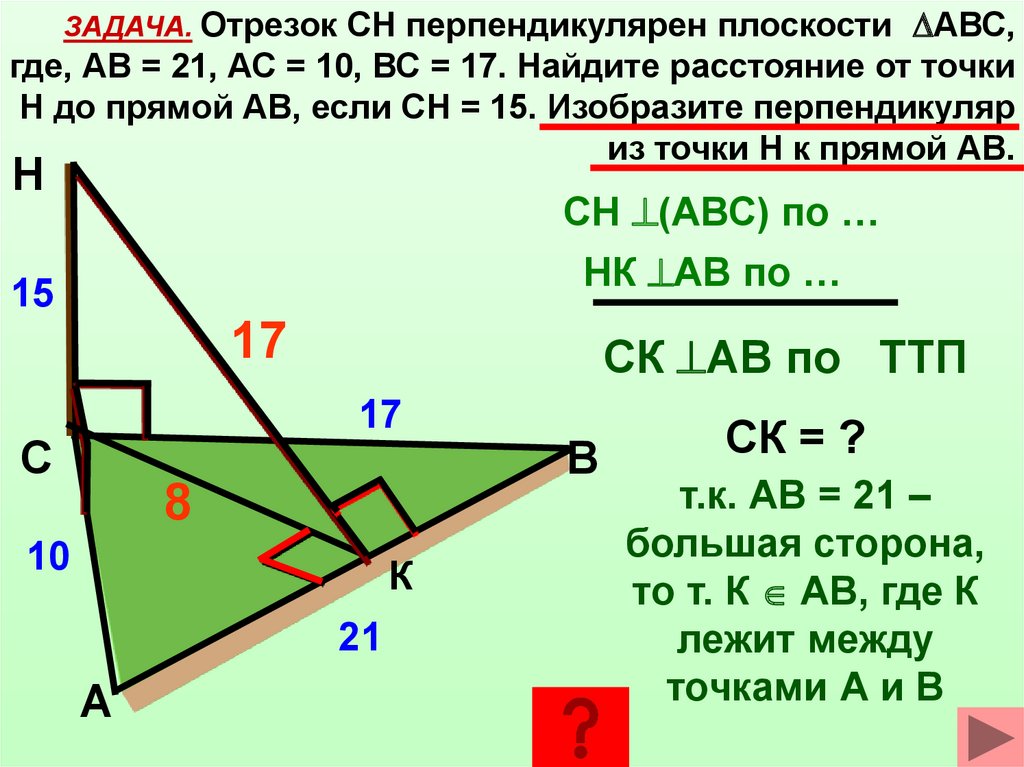
ЗАДАЧА. Отрезок СН перпендикулярен плоскости АВС,
где, АВ = 21, АС = 10, ВС = 17. Найдите расстояние от точки
Н до прямой АВ, если СН = 15. Изобразите перпендикуляр
из точки Н к прямой АВ.
Н
СН (АВС) по …
НК АВ по …
15
17
СК АВ по ТТП
17
С
8
10
К
21
А
В
СК = ?
т.к. АВ = 21 –
большая сторона,
то т. К АВ, где К
лежит между
точками А и В

15.

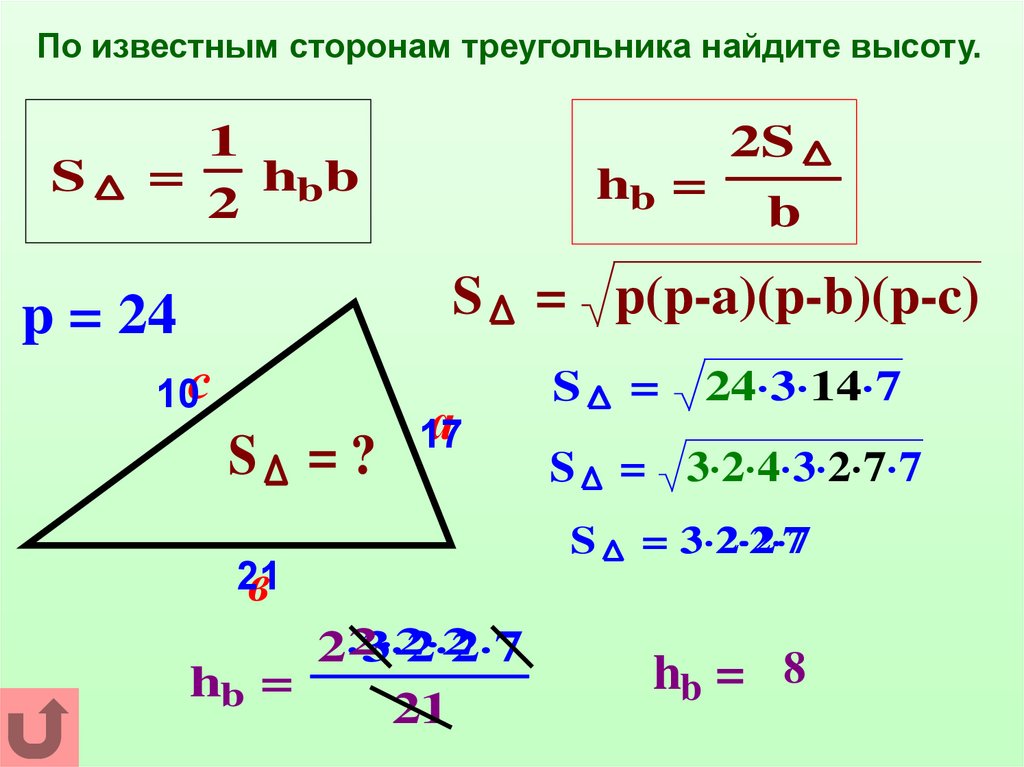
По известным сторонам треугольника найдите высоту.
S
1
=
hbb
2
2S
hb =
b
S = p(p-a)(p-b)(p-c)
p = 24
10с
S =?
а
17
21
в
2 2 2
2 3 2 2 7
hb =
21
S
=
S
= 3 2 4 3 2 7 7
S
24 3 14 7
= 3 2 2 7
3 2 2 7
hb = 8

16.

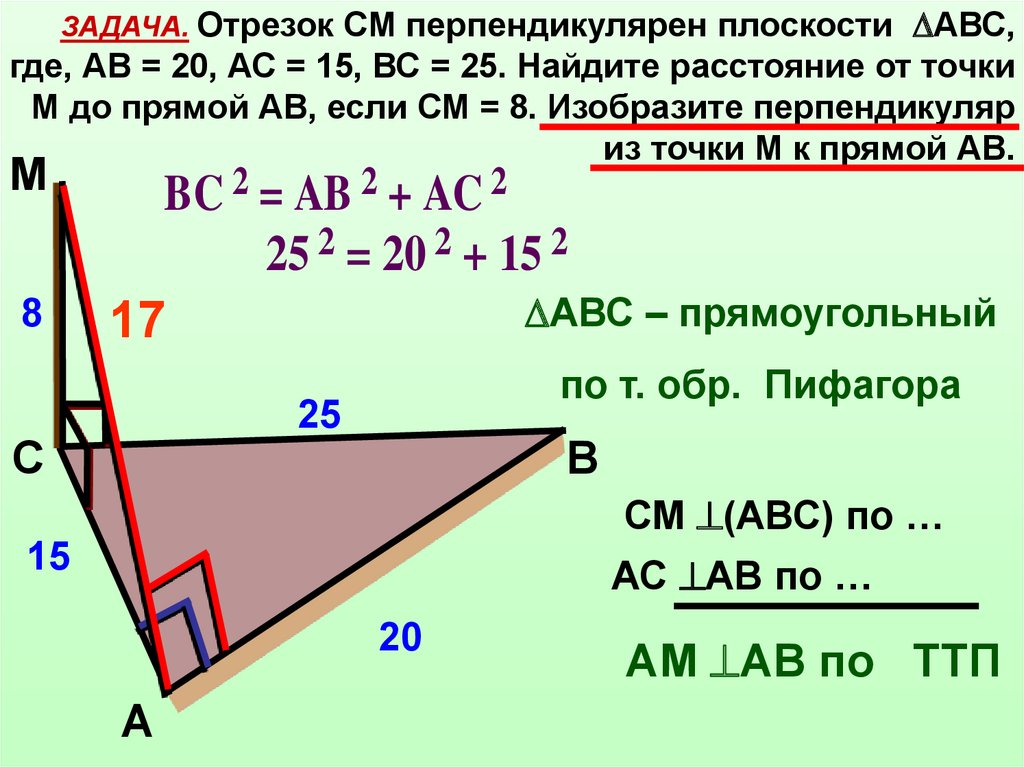
ЗАДАЧА. Отрезок СМ перпендикулярен плоскости АВС,
где, АВ = 20, АС = 15, ВС = 25. Найдите расстояние от точки
М до прямой АВ, если СМ = 8. Изобразите перпендикуляр
из точки М к прямой АВ.
М
8
BC 2 = AB 2 + AC 2
25 2 = 20 2 + 15 2
АВС – прямоугольный
17
по т. обр. Пифагора
25
С
В
СМ (АВС) по …
15
АС АВ по …
20
А
АМ АВ по ТТП