Похожие презентации:
Градусная и радианная мера угла
1.
Градуснаяи радианная
мера угла
2.
Цели занятия:1. Изучить способы измерения углов в градусах и
радианах;
2. Сформировать умение пользоваться измерением
углов при решении практических задач.
Компетенции по ФГОС:
• применять математические методы для решения
профессиональных и прикладных задач;
• использовать приемы и методы математического
анализа в различных профессиональных ситуациях;
• анализировать результаты измерения величин с
допустимой погрешностью, представлять их графически.
3.
Тригонометрия в искусстве4.
Тригонометрияв пожарной службе
α
5.
Тригонометрия в авиации6. Тригонометрия в биологии
7.
8.
Тригонометрия(«три» - три, «гониа» - угол,
«метриа» - измеряю)
раздел математики,
изучающий
соотношение сторон и
углов в треугольнике
9.
Чему равен угол квадрата?0
90
10.
На какой угол поворачиваетсясолдат по команде «кругом»?
0
180
11.
Чему равен угол между минутной ичасовой стрелками на часах,
когда они показывают 2 часа?
0
60
12.
Единицыизмерения углов
Градусы
Радианы
13.
Градусная мера угла=1
1 – цена одного деления
окружности, разделенной на
360 частей
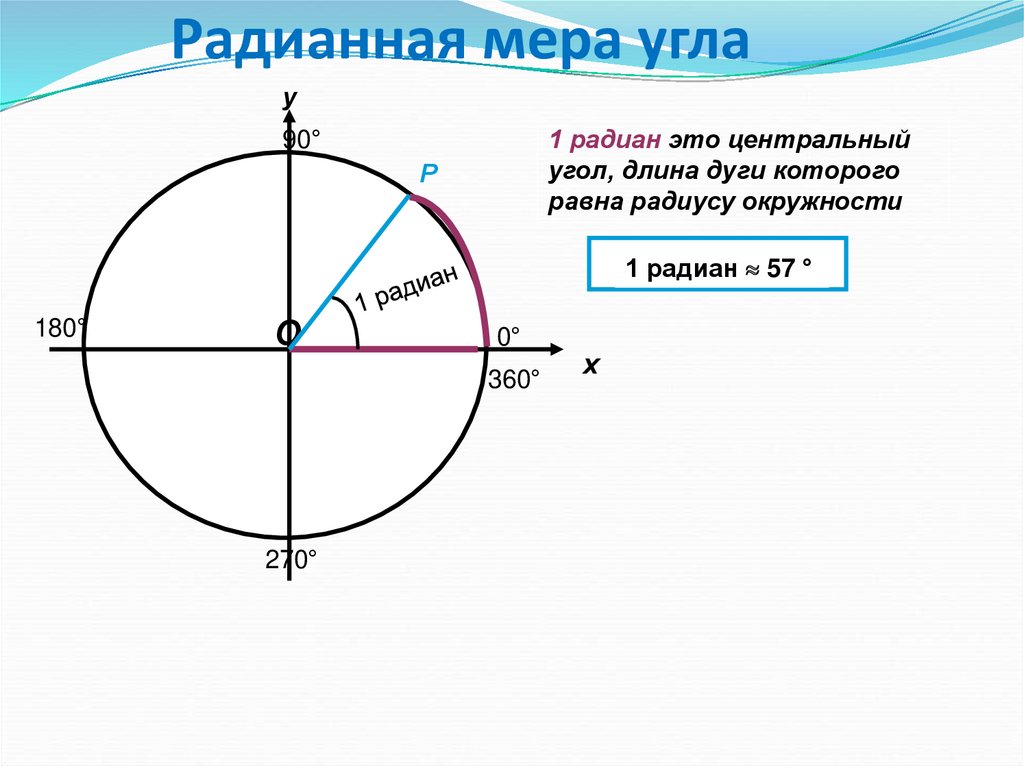
14. Радианная мера угла
у1 радиан это центральный
угол, длина дуги которого
равна радиусу окружности
90°
Р
1 радиан 57 °
180°
О
0°
360°
270°
х
15.
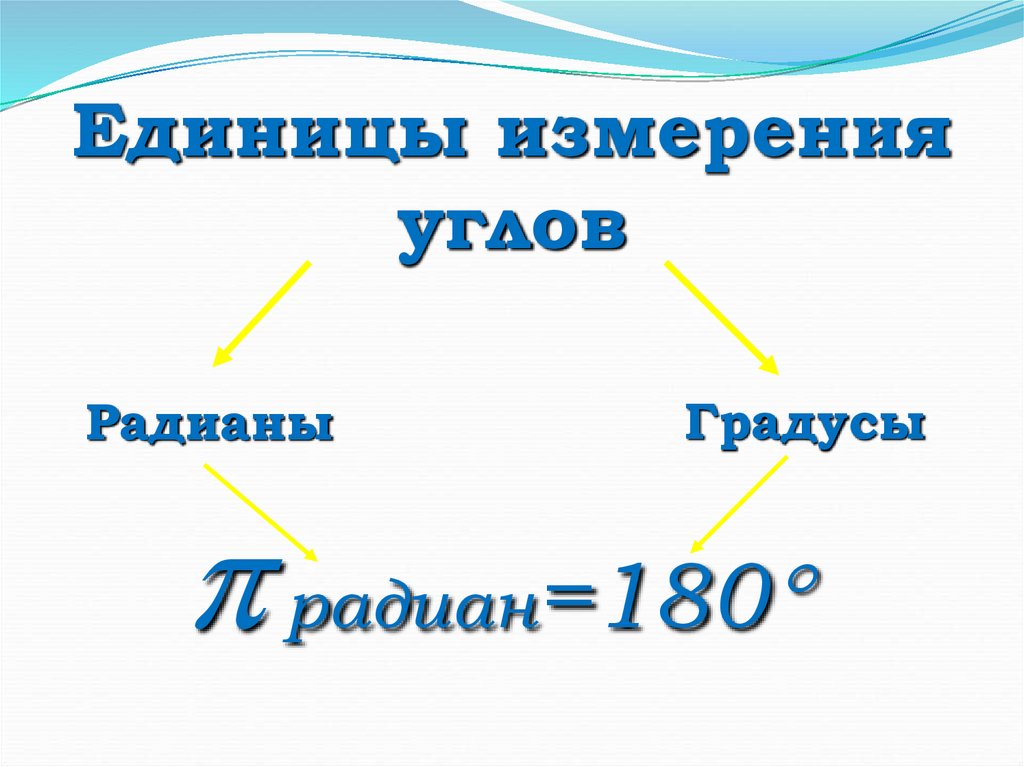
Единицы измеренияуглов
Радианы
Градусы
радиан=180
16.
Перевод из градусноймеры в радианную:
радиан=180
рад
17.
Пример:1.
2.
18.
Перевод из радианноймеры в градусную:
радиан=180
19.
Примеры:1.
2.
20.
Таблица перехода изградусной
в радианную меру угла
Градусы 0 30
45
60
6
4
3
Радианы
0
900
120 135 150 180 270
2
2 3
3 5
4 6
3
2
3600
2
21.
22.
23.
24.
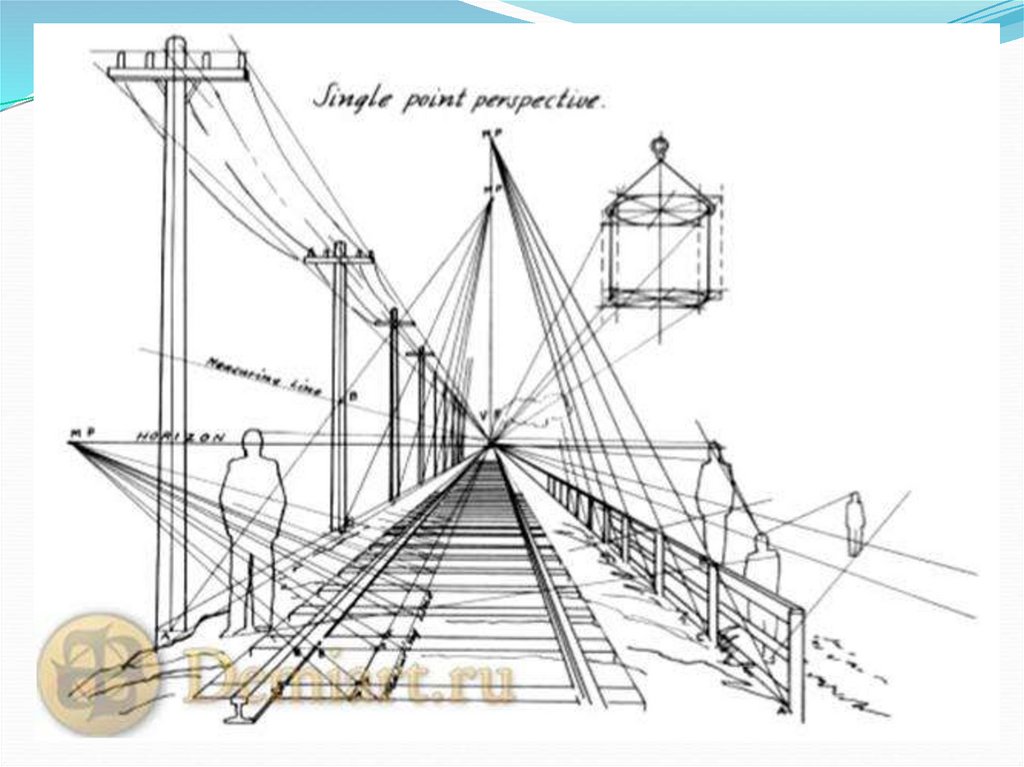
Точка осмотра 3D рисунковдля зрителей
25. Практическая работа
Первый шаг. Нам понадобится жесткая бумага. Сгибаем листровно по середине. Рисуем в обе стороны прямые линии
под одинаковым углом. Линии должны зеркально отражать
друг друга. Примерно 35-40 градусов.
26.
Второй шаг. Рисуем ступеньки лестницы с двухсторон, параллельно сгибу листа.
27.
Третий шаг. Берем линейку и соединяем прямой линиейвершины лестницы. Это будет тень. Берем мягкий
карандаш и делаем тень. Давить на карандаш не стоит,
тень не должна быть слишком темной.
28.
Последний шаг. Поднимаем одну часть бумаги вверх иразворачиваем бумагу под углом к зрителю. Важно
подобрать такой угол, чтобы лестница казалась прямой.
Из-за тени будет казаться, что это объемный рисунок:
29.
http://wikibit.me/v/30. Вывод:
Мы узнали, что тригонометрияприменяется не только в алгебре и
началах анализа, но и в строительстве,
пожарной службе, биологии и т.д.
Тригонометрия является основой для
создания многих шедевров архитектуры;
Научились использовать тригонометрию
в задачах с практическим содержанием.
























 Математика
Математика








