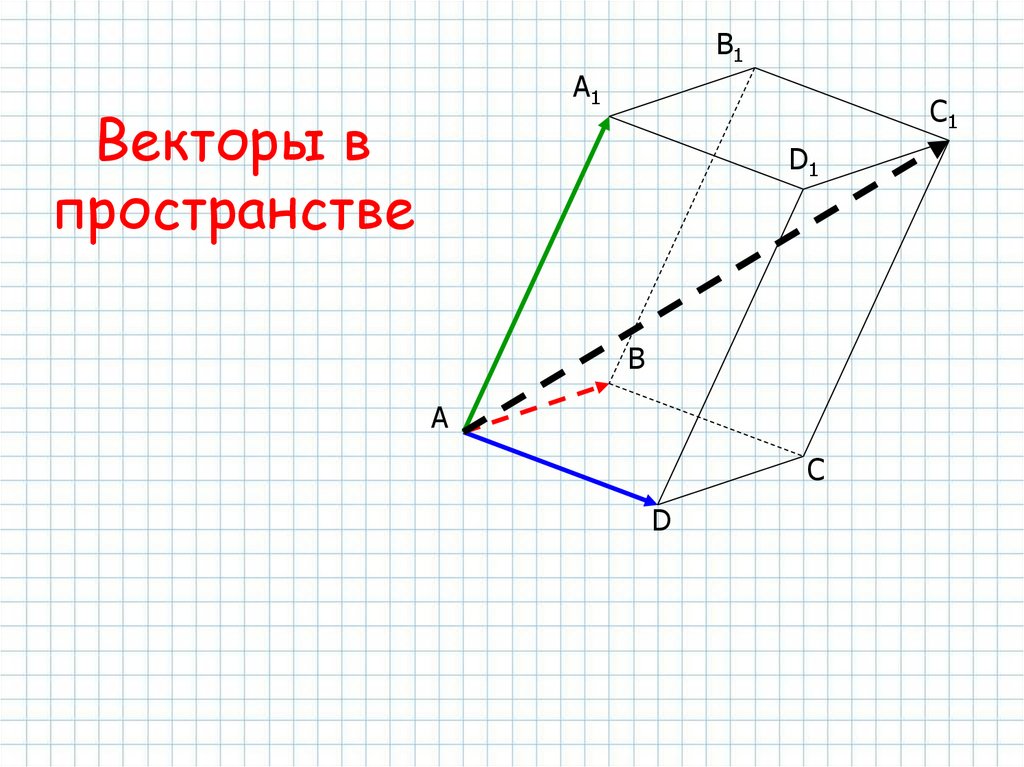
Векторы в пространстве

1.

B1
A1
Векторы в
пространстве
C1
D1
B
A
C
D

2.

Определение вектора.
Как и на плоскости, в пространстве вектор определяется как направленный
отрезок:
B
A
Точка А – начало вектора, В – конец вектора. Записывают: AB или
a.
Вектор, у которого начало совпадает с конечной точкой называется нулевым,
обозначается: 0 или AA .
0
Длина отрезка, изображающего вектор, называется модулем вектора, т.е.

3.

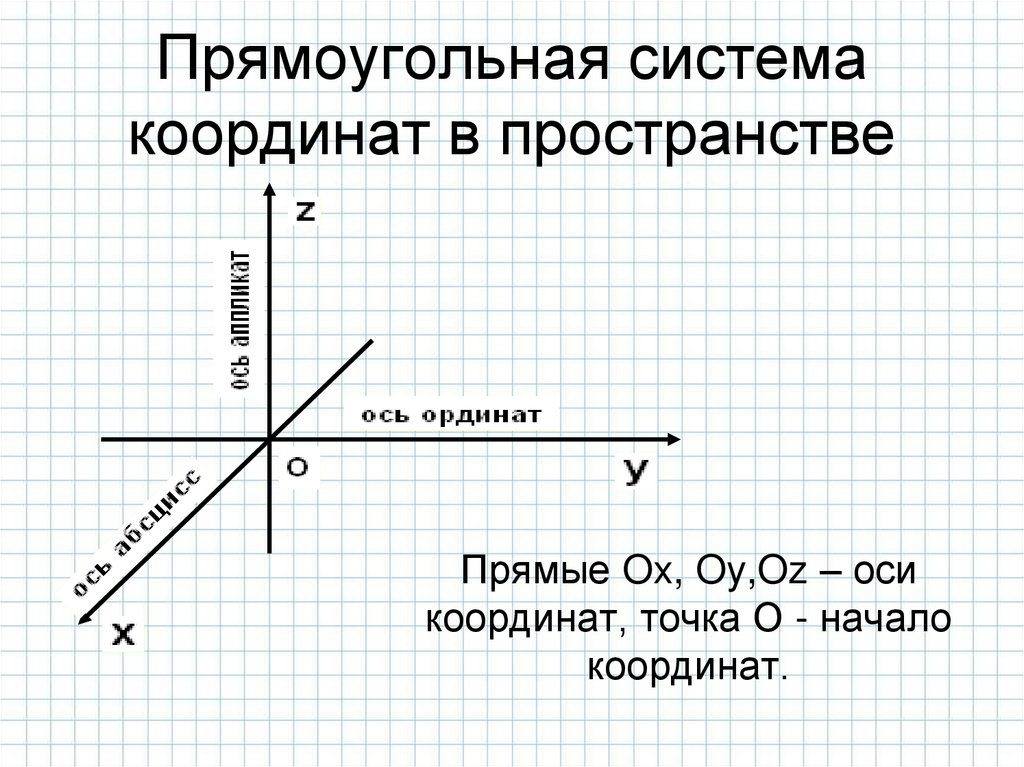
Если через точку
пространства
проведены три попарно
перпендикулярные
прямые, на каждой из них
выбрано направление и
выбрана единица
измерения отрезков, то
говорят, что
задана система
координат в
пространстве.

4. Прямоугольная система координат в пространстве

Прямые Ox, Oy,Oz – оси
координат, точка О - начало
координат.

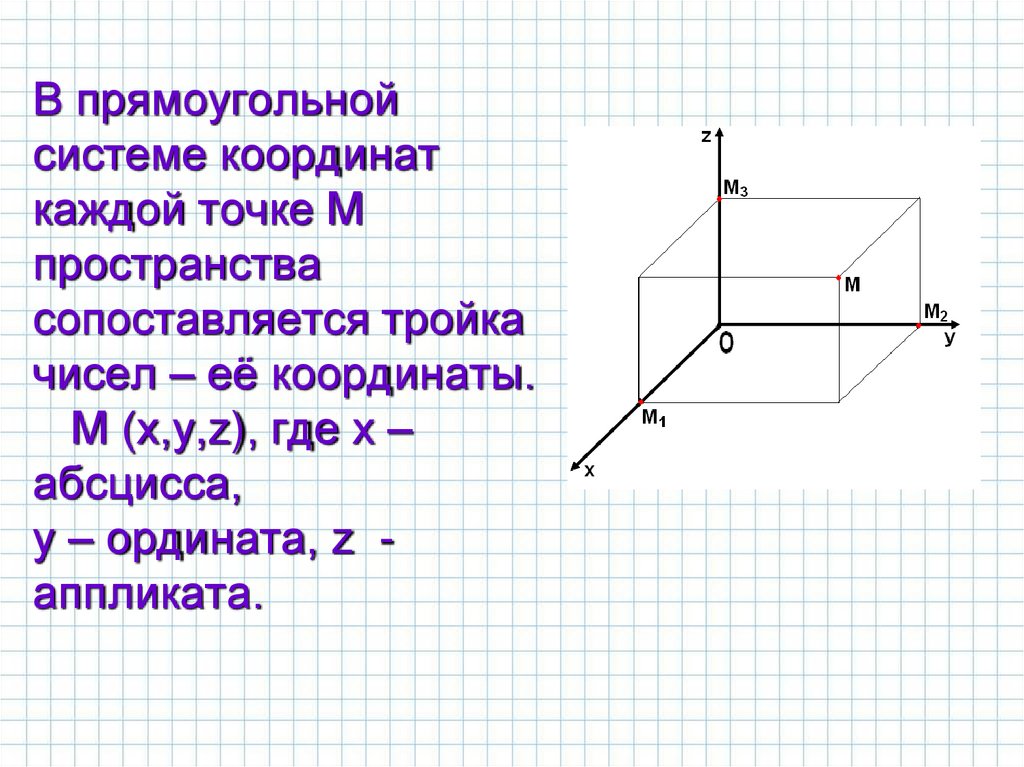
5. В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел – её координаты. М (х,у,z), где х –

абсцисса,
у – ордината, z аппликата.

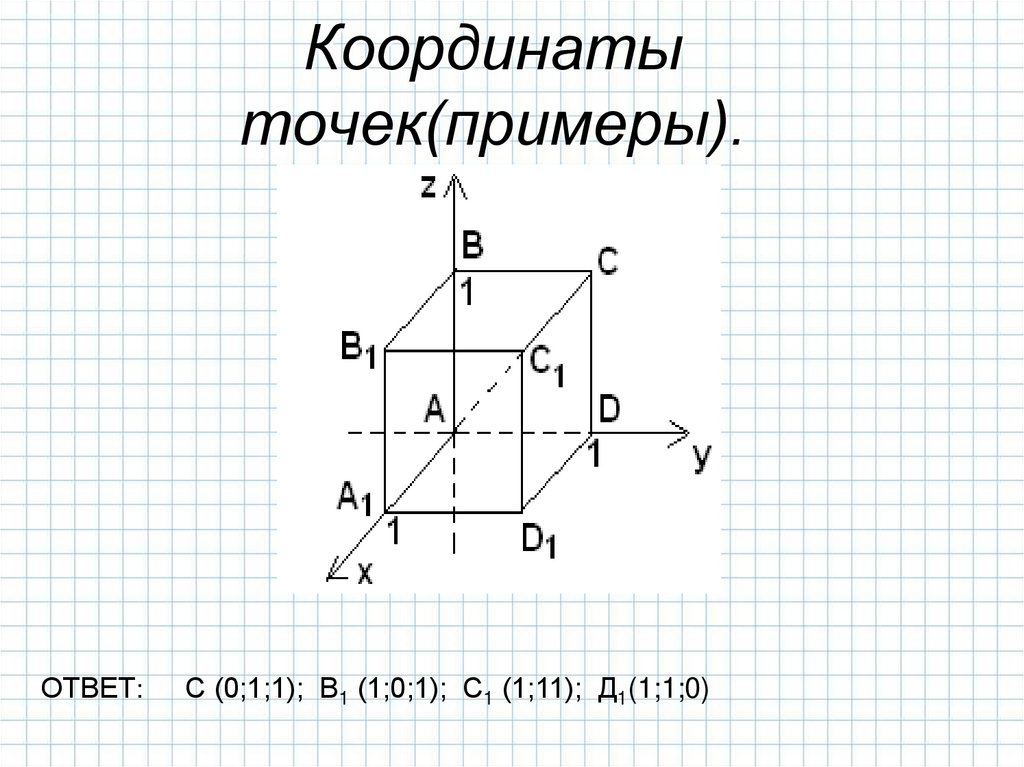
6. Координаты точек(примеры).

ОТВЕТ:
С (0;1;1); В1 (1;0;1); С1 (1;11); Д1(1;1;0)

7. Координаты вектора

8.

Координаты вектора.
В прямоугольной системе координат в
пространстве векторы i 1;0;0 , j 0;1;0
k 0;0;1
z
называются
векторами
единичными ( базовыми)
k
i
O
x Любой вектор
j
y
по координатным векторам
a можно разложить
a xi yj zk

9.

Действия с векторами в координатах
a{x1 , y1 , z1}
b { x2 , y 2 , z 2 }
10.Чтобы найти сумму векторов, надо сложить их соответствующие
координаты, т.е.
{x1 x2 ; y1 y2 ; z1 z2}
20. Чтобы найти разность векторов, надо вычесть их соответствующие
координаты, т.е.
{x1 x2 ; y1 y2 ; z1 z2}
30. Чтобы найти произведение вектора на число , надо координаты вектора
умножить на число

10. Примеры

ДАНО:
РЕШЕНИЕ:
a b {3 0; 5 7;2 ( 1)} {3;2;1}