Похожие презентации:
Прикладные методы расчёта конструкций РКТ
1.
Литература по курсу «Прикладные методырасчёта конструкций РКТ»
1. Бутенин Н.В. и др. Курс теоретической
механики. Том II. М.: 1985. гл. 2, 19, 20, 28.
2. Бишоп Р. Колебания. М.: 1979.
3. Магнус К. Колебания: Пер с нем. – М.: Мир,
1982. – 304 с.
4. Яблонский А. А., Норейко С. С. Курс теории
колебаний. М.: Высшая школа. 1975.
5. Пановко Я. Г. Введение в теорию
1
механических колебаний. М.: 1980, 1991.
2.
6. Мигулин В. В. и др. Основы теории колебаний.М.: Наука, Гл. ред. физ-мат лит. 1978.7. Светлицкий В. А., Стасенко И. В. Сборник задач
по теории колебаний. М.: 1979.
8. Вибрации в технике: Справочник. В 6-ти т. / Ред.
Совет: В. Н. Челомей (пред.) М.: Mашиностроение, 1978. Т.1: Колебания линей-ных
систем / Под ред. В. В. Болотина, 352 с.
9. Ильин И. М. и др. Теория колебаний: Учеб. Для
вузов / Под общей ред. К. С. Колесникова. – М.:
Изд-во МГТУ им. Н. Э. Баумана, 2001. – 272 с. –
(Сер. Механика в техн. ун-те; Т.4)
10. Калашников Б. А. Нелинейные колебания
механических систем: Учеб. пособие. – Омск:
ОмГТУ, 2006. – 206 с.
2
3.
СПИСОК ПРИНЯТЫХ СОКРАЩЕНИЙАТТ – абсолютно твёрдое тело;
МС – механическая система;
3
4.
1. ПОНЯТИЕ ЖЁСТКОСТИ СИСТЕМЫ СОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
4
5.
56.
Рис. 1.1. Колебательные системы с одной поступательной
степенью свободы q:
а – линейная МС – груз на пружине;
б нелинейная МС – осциллятор Дуффинга
6
7.
7Рис.1.2
. Колебательные системы с одной угловой
степенью свободы
а – восстанавливающий элемент
два последовательно соединённых торсиона
с диском или тонким ободом на конце;
б математический маятник;
при малых угловых перемещениях обе МС
могут считаться линейными
8.
n1
2
П q ci i q ;
2 i 1
q
F q
;
q
.
F П
c
2 ;
q q
2
8
9.
9a
б
С.5
Рис. 1.3 Примеры линейных колебательных МС с
одной степенью свободы:
а –параллельно-последовательное соединение пружин;
б – последовательное соединение торсионов
10.
qДля схемы
На рис. 1.1 а
Для схемы
На рис. 1.3 а
;
10
1 2 q
c1
c2
; 2 q
1 q
c1 c2
c1 c2
4
Gdi
GJ
ci
p ,i
3
ci
8Di ni
q
li
1
1
2
2
П с1 1 с2 2
2
2
1 с1с2 2
П
q
2 с1 с2
11.
с1с2ceq
с1 с2
11
eq 1 2 q
С.6
ceq с1 с2
eq 1 2 q
С.6
12.
12Рис. 1.4
.Нелинейная зависимость
деформации упругого элемента в
С.6
осцилляторе Дуффинга обусловлена
ортогональностью оси пружины и
вектора перемещения q
13.
131
2
П q c0 q ;
2
1
1
2
П q c0 q c0
2
2
q l l s0
2
2
> П(q):=taylor(П(q), q=0, 6);
S0 q
1 s0 2 1
П q c0 q 2 1
2 l
2l
l 4
1 2 1 4
c1q ck q ;
2
4
4
14.
s0ceq c1 c0
l
s0 0
3
cq
F q 2
2l
c0
s0
ck 2 1
2l
l
4
c0 q
2
8l
ceq c1 0
F 3cq
c q
2
q
2l
2
14
14
15.
в)а)
б)
15
16.
а)а
б)
г)
в)
16
17.
4Gd
c
8 D 3n
E
G
, = 0,3 – для стали;
2 1
,
T
N
2
соб
с
m
соб
c m
2
соб
2
Т
17
18.
Введение18
19.
1920.
2021.
2122.
2223.
2324.
К. МАГНУС, СТР. 10624
25.
2526.
qq
г)
a)
M
ж)
q
q
M
С
в)
q
д)
2r
б)
а
з)
M
е)
26
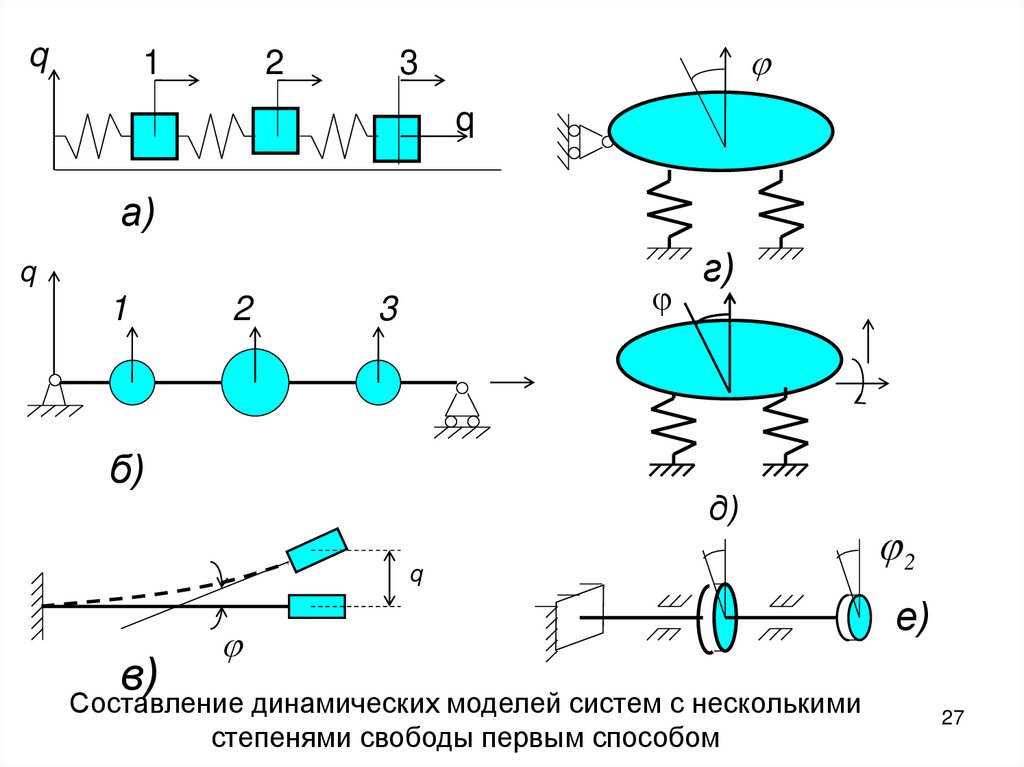
27.
q1
2
3
q
а)
q
1
2
3
б)
г)
д)
q
в)
Составление динамических моделей систем с несколькими
степенями свободы первым способом
2
е)
27
28.
Дискретизация распределенной системыпо второму способу. Пример:
c
c
c
28
29.
Характеристика сил, действующих при колебаниях МС1. Силы, зависящие от времени:
Mq q cq F( t )
Mq qотн cqотн 0
q qотн x
Mqотн qотн cqотн Mx
Предположим, что..
x x0 cos t
F t Mx Mx0 cos t
2
29
30.
• 8 октября 2018года . Лекция №530
31.
M восст mgL sin2. Позиционные силы:
mgL
M восст mgL sin 0
cos 0 ( 0 )
1!
mgL
mgL
2
sin 0 ( 0 )
cos 0 ( 0 )3
2!
3!
mgL 3
M восст mgL
...
6
0,1 3 0.001
Если
, то
1 , то
mgL
Если
M восст
M восст c
0,001
0,16%
6 0,1
6
6
1
100% 17%
6 1
c mgL , Нм
31
32.
Для схемы :Для схемы :
c c0 L mgL
2
c c0 L mgL
а)
2
б)
П : П1 П 2 ;
1
П1 : mgL 1 cos ; П1 mgL 2 ;
2
1
2
П 2 : c L
2
П : П;
32
33.
Mg p0 pокр SMg pокр S p0 S
pV p0V0 ;
p0V0
h
p
p0
V0 Sq
h q
33
34.
p0 ShFвосст q Mg pокр S
;
h q
h
Fвосст q p0 S 1
;
h q
1
q
Fвосст Q 1
;Q
1 Q
h
34
35.
> Res:=taylor((p_0*V_0/(V_0+S*q)-p_okr)*S,q=0,2);
p_0 S 2
Res := ( p_0 p_okr ) S
q O( q 2 )
V_0
> Res:=convert(Res, polynom);
p_0 S 2 q
Res := ( p_0 p_okr ) S
V_0
Уравнение равновесия:
> eq:=M*g=(p_0-p_okr)*S;
eq := M g ( p_0 p_okr ) S
35
36.
Восстанавливающая сила:2
p_0 S q
> F_rest:=rhs(eq)-Res; F_rest :=
V_0
2
p_0 S
c :=
V_0
Производная точной силы в нуле
> c:=diff((M*g-(p_0*V_0/(V_0+S*q)-p_okr)*S),q);
2
p_0 V_0 S
c :=
( V_0 S q ) 2
> q:=0; c:=c;
q := 0
p_0 S 2
c :=
V_0
p0 S
с
h
36
37.
Fвосст сqПодробности и дальнейшее
рассмотрение в книге
Калашников Б.А.
«Нелинейные колебания
механических систем».
Омск-2006г. 206 стр. На Стр. 20.
37
38.
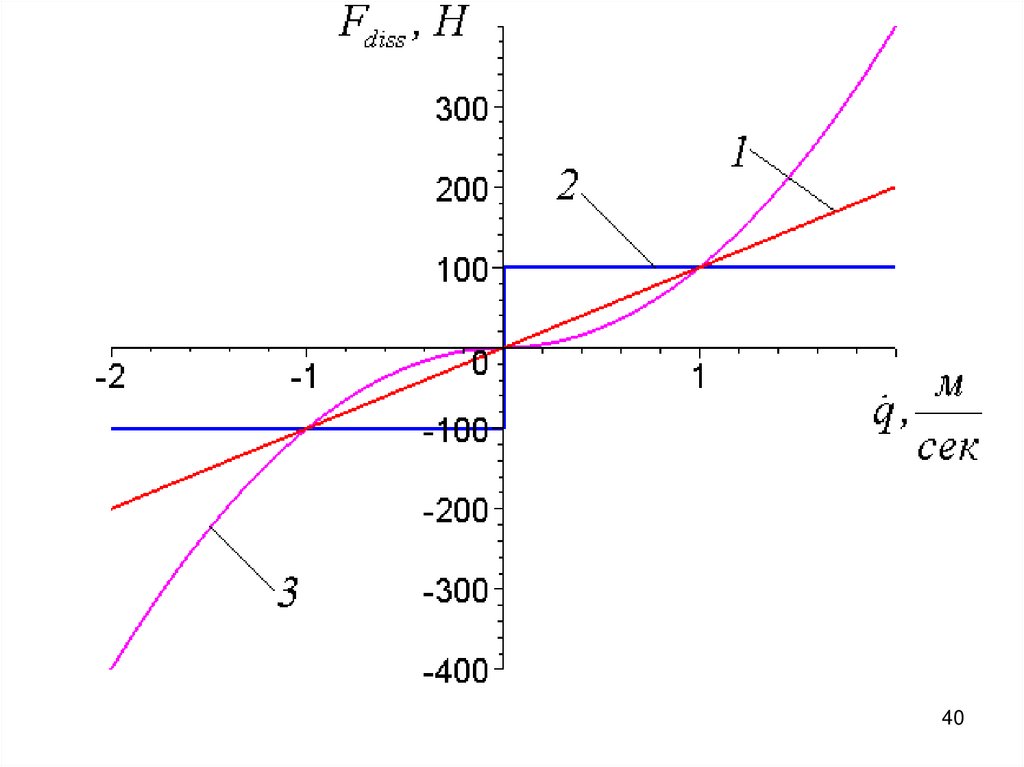
3. Силы, зависящие от относительной скоростиFдисс q 1qотн
F q 0 sign q
– сила линейного неупругого
сопротивления (трения);
– сила сухого трения;
F q n q sign q
n
– сила нелинейно-вязкого трения
или:
Fдисс q n qотн
n 1
qотн
F q 1q 3 q 5 q ..
3
5
38
(с. 33 НКМС - 2006) ЛР .№3 В НКМС-2006, СТР . 107
39.
3940.
4041.
Точное значение коэффициента2
(квадратичное трение) для гидравлического
амортизатора:
41
42.
НH м
1
м / сек с
Q f др
2 p
Q Sqотн
S
Fдисс p S
Fдисс qотн
S
3
2 f др
2
qотн qотн ;
2
S 3
2 f др42
2
43.
Зависимость диссипативных сил ототносительного перемещения
qотн Aотн cos t qотн Aотн sin t
2
sin t 1 cos t
q
отн
n
sin t 1
Aотн
Fдисс qотн n qотн
n
n
2 2
sign qотн n qотн
n 1
(*)
qотн
43
44.
qFдисс qотн n Aотн 1 отн
Aотн
n
nl
F , дисс
A
n Aотн
2
n
2
n
НКМС – 2006, СТР. 35-36
44
45.
4546.
c 100 Н м12 с
1
0<n<1
n=0
n=1
n=2
n>2
46
47.
Найдём количество… …линейной силой тренияв линейной по восстанавливающей силе системе
qотн Aотн cos t
lin
diss
F
qотн Aотн sin t
Возводя в квадрат qотн
2
qотн Аотн sin t
и
lin
Fdiss
, получим
2
qотн F
1
Аотн Аотн
lin
diss
a Аотн b Аотн W
S ab
A
2
отн47
48.
Q q,tQ(q, q )
48
49.
Свободные колебания МСУравнение Лагранжа II рода:
d T T
П
dt q q
q
Если
ri
-радиус-вектор i-ой точки определяется только
-одной обобщённой координатой
q
и не зависит явно от времени, то
n
n
1
1
2
T mi i mi i i
2 i 1
2 i 1
d ri ri
1 2
ri
i
q и тогда T q mi
2 i 1 q
dt q
n
49
2
50.
riA q mi
i 1
q
n
2
q 0
A 0 2
A q A 0 A 0 q
q ..
2!
1 2
T aq
A 0 a
2
П П q
П 0 2
П q П 0 П 0 q
q ...
2!
50
51.
П 0 0; П Fвосст q и Fвосст 0 0;1 2
П cq , где с П 0
2
П 0 0; c 0 c 0
Движение происходит вблизи устойчивого состояния
статического равновесия.
51
52.
aq cq 0; собq
2
соб
с
;
a
q 0;
q C1 sin coб t C2 cos соб t;
q 0 q0 и q 0 q0
C1
q0
соб
; C2 q0
52
53.
> eq_1:=q =C_1*sin(omega*t)+C_2*cos(omega*t);
> eq_2:=q_v=diff(rhs(eq_1),t);
> Sys:=[eq_1, eq_2];
> B:=[C_1, C_2];
> Res:=solve (Sys, B);
> Res:=subs(t=0, q=q_0, q_v=q_v_0, Res);
> C_1:=rhs(Res[1][1]);
> C_2:=rhs(Res[1][2]);
53
54.
ВЫДЕЛЕНИЕ ИЗ СПИСКА СПИСКОВПОСТОЯННОЙ С_1:
> C_1:=rhs(Res[1][1]);
( rhs - правая часть от
q_v_0
C_1 :=
right hand side)
И
ВЫДЕЛЕНИЕ ИЗ СПИСКА СПИСКОВ
ПОСТОЯННОЙ С_2:
> C_2=rhs(Res[1][2]);
C_2 := q_0
В ИТОГЕ ПОЛУЧАЕМ ПОСТОЯННЫЕ
ИНТЕГРИРОВАНИЯ В ВИДЕ:
С1
q0
cоб
С2 q0
54
55.
qq0
соб
q0
соб
sin соб t q0 cos соб t
q0 С2 Asin
С1 Acos
qгде A sin
q Asin собt ,
t , где
соб
2
q0
соб q0
2
A
q0 ; arctg
q0
соб
55
56.
собРис. Собственные гармонические колебания линейной
56
системы с одной степенью свободы
57.
Следует заметить, что амплитудасобственных незатухающих колебаний :
q0
A q
соб
2
2
0
определяется только начальными условиями,
а частота собственных незатухающих колебаний:
соб
с
1
,
c
.
a
Период собственных незатухающих колебаний:
2 .
T
соб
57
58.
Линейные диссипативные системыс одной степенью свободы
d T T
П
Fdiss
dt q q
q
Fdiss - обобщённая сила линейного трения
Примем, что на каждую точку системы..
Ri i i
i - коэффициент трения
Основное выражение
для обобщённой силы:
ri
F Ri
q
i 1
n
58
59.
ri iq q
и соотношение
ri
i
i i
i i
q
q
i 1
i 1
n
Fdiss
С их учётом:
n
Так как
i 1
1
i
i i
q 2 q
2 q
2
i ,
n
то
Fdiss
i 1
i
2 q
q i 1 2
2
i
n
2
i i
59
60.
nСумма
i 1
2
i i
формальна сходна с T, и её называют
диссипативной функцией Рэлея
2
1 2
Ф q
2
Fdiss
- обобщённый коэффициент
вязкого (линейного)
трения, или сопротивления.
Ф
q
q
aq q cq 0
Х. уравнение:
Частное
решение:
a c 0
2
e
t
60
Его корни:
61.
1,24ac
2a
2
, где
h h
2
Вынося
соб
2
соб
и обозначая
1,2 соб 1
Если
q e
2
h
соб
h
2a
2 ca
1
1,2 соб i 1
C
sin t C2 cos t
ht
1
*
соб
2
*
соб61
62.
*соб
2
соб
h соб 1
2
2
t 0 : q 0 q0 ; q 0 q0
C1
q0 hq0
*
соб
; C2 q0
C1 Asin ; C2 Acos
q Ae
ht
, где
sin t
*
соб
62
63.
Aq0 hq0
*2
соб
2
q
2
0
C2
q0
tg
C1 q0 hq0
*
соб
63
64.
ПРОПУСТИТЬ,ПО ДРУГОМУ ПУТИ!
64
65.
> restart;q:=exp(-h*t)*
((C_1+C_2)*cos(omega*t)+
I*(C_1-C_2)*sin(omega*t));
q := e
( h t )
( ( C_1 C_2 ) cos( t ) ( C_1 C_2 ) sin ( t ) I )
> q_v:=diff(q,t);
q_v := h e
e
( h t )
( h t )
( ( C_1 C_2 ) cos( t ) ( C_1 C_2 ) sin ( t ) I )
( ( C_1 C_2 ) sin ( t ) ( C_1 C_2 ) cos( t ) I )
>t:=0; eq_1:=q_0=q; eq_2:=q_v_0=q_v;
t := 0
eq_1 := q_0 C_1 C_2
eq_2 := q_v_0 h ( C_1 C_2 ) ( C_1 C_2 ) I
65
66.
> sys:=[eq_1,eq_2];sys := [ q_0 C_1 C_2 , q_v_0 h ( C_1 C_2 ) ( C_1 C_2 ) I ]
> B:=[C_1,C_2];
B := [ C_1 , C_2 ]
1
I ( q_v_0 q_0 h q_0 I )
q_0 q_v_0 I q_0 h I
2
Res := C_1
, C_2
2
> Res_1:= (Res[1]);
66
67.
> Res_1:= (Res[1]);1
I ( q_v_0 q_0 h q_0 I )
q_0 q_v_0 I q_0 h I
2
Res_1 := C_1
, C_2
2
> C_1:=rhs(Res_1[1]);
q_0 q_v_0 I q_0 h I
C_1 :=
2
> C_2:=rhs(Res_1[2]);
1
I ( q_v_0 q_0 h q_0 I )
2
C_2 :=
67
68.
> С2:=C_1+C_2;1
I ( q_v_0 q_0 h q_0 I )
q_0 q_v_0 I q_0 h I 2
Ñ2 :=
2
> C2 := simplify( С2, 'symbolic' );
C2 := q_0
C1:=I*(C_1-C_2);
1
I ( q_v_0 q_0 h q_0 I )
q_0 q_v_0 I q_0 h I 2
I
C1 :=
2
> C1 := simplify(C1, 'symbolic' );
q_v_0 q_0 h
C1 :=
68
69.
• ДРУГОЙ ПУТЬ:ДЛЯ СОВРЕМЕННЫХ
СТУДЕНТОВ
69
70.
> restart;q:=exp(-h*t)*(C_1*sin(omega*t)+C_2*
cos(omega*t));
q := e
( h t )
( C_1 sin ( t ) C_2 cos( t ) )
> q_v:=diff(q,t);
q_v :=
h e
( h t )
( C_1 sin ( t ) C_2 cos( t ) ) e
( h t )
( C_1 cos( t ) C_2 sin ( t ) )
> t:=0; eq_1:=q_0=q;
eq_2:=q_v_0=q_v;
t := 0
eq_1 := q_0 C_2
eq_2 := q_v_0 h C_2 C_1
70
71.
> sys:=[eq_1,eq_2];sys := [ q_0 C_2 , q_v_0 h C_2 C_1 ]
> B:=[C_1,C_2];
B := [ C_1 , C_2 ]
> Res:=solve(sys, B);
q_v_0 h q_0
Res := C_1
, C_2 q_0
> Res_1:= Res[1];
q_v_0 h q_0
Res_1 := C_1
, C_2 q_0
71
72.
> C_1:=rhs(Res_1[1]);q_v_0 h q_0
C_1 :=
> C_2:=rhs(Res_1[2]);
C_2 := q_0
72
73.
Aог t Ae ; Tht
A t
A t T
; hT h
*
e
hT *
2
*
соб
1
2
*
Разлагая..
*
соб 1
2
;
*
соб
соб
2
1
2
> taylor (2 * Pi * psi / sqrt(1 psi^2), psi = 0, 3);
3
2 O( )
2
73
74.
21
2
соб
*
соб
Зависимость декремента и отношения частот от коэф отн затух
соб
*
соб
74
75.
Если1
, то такой осциллятор называется
передемпфированным.
aq q cq 0 1,2 соб 2 1
Оба корня – вещественные и отрицательные.
1t
q C1e C2 e
2t
q0 2 q0
q0 1q0
C1
; C2
1 2
2 1
75
76.
restart;q:=C_1*exp(lambda_1*t)+C_2*exp(lambda_2*t)
;
Произвольные постоянные
> C_1:=(q_v_0-lambda_2*q_0)/(lambda_1lambda_2);
q0 2 q0
>
C1
1 2
> C_2:=(q_v_0-lambda_1*q_0)/(lambda_2lambda_1);
q_v_0 lambda_1 q_0
C_2 :=
lambda_2 lambda_1
76
77.
> lambda_1:=- соб *psi+sqrt(psi^2-1);> lambda_2:=-
соб *psi-sqrt(psi^2-1);
РИСУНКИ К КУРСУ ТК\Затух при psi больше 1.mws
psi:=1.2; q_v_0:=1.0*i; q_0:=0.1;
q:=q;
q := (.7537783615*i+.1404534034)*exp(-.5366750419*t)+
(-.7537783615*i-.4045340337e-1)*exp(-1.863324958*t)
t_min:=0; t_max:=5;q_min:=-0.4;
q_max:=+0.4;
seq_q_v_0:=plot ( [seq (q, i = [-1,0,1] ) ], t=t_min..t_max,
thickness=2, colour=[RED, BLUE, GREEN]):
77
78.
with (plots):Net:=coordplot ( cartesian,
[ t_min..t_max, q_min..q_max],
сolor = [black,black], grid=[5,5],
view = [t_min..t_max, q_min..q_max+0.04],
ytickmarks=4):
> display(seq_q_v_0, Net);
78
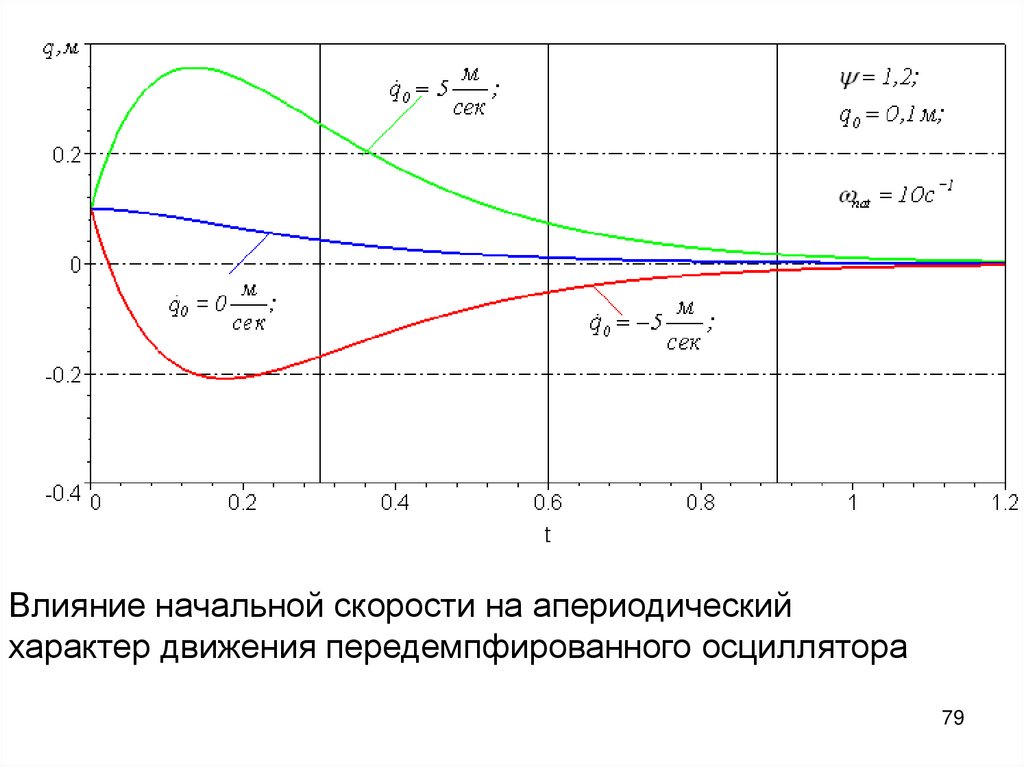
79.
Влияние начальной скорости на апериодическийхарактер движения передемпфированного осциллятора
79
80.
Если1
q e
соб t
Пример:
,
решение имеет вид:
q0 q0 соб q0
Ai
1
hT ln
ln
0,511
Ai 1
1 0,4
*
> restart;
> eq:=2*pi*psi/sqrt(1-psi^2)=0.511;
eq :=
2
1
2
0.511
> psi:=solve(eq,psi);
:=
511.
261121. 0.4000000 10
7
2
,
511.
261121. 0.4000000 10807 2
81.
> pi:=evalf(Pi);> psi_1:=psi[1];
psi_1 := 0.08106053952
Влияние трения на собственную частоту:
> omega_s_s:=omega_s*sqrt(1-psi_1^2);
omega_s_s := 0.9967091797 omega_s
81
82.
Каноническая форма1
aq q cq 0
q Ae
ht
cos
*
соб
t
82
83.
c tdq dq d
q
c q
dt d dt
dq dq d
2
q
c q
dt d dt
a c q c q c q 0
c
q
q
q
0
2
a c
a c
2
83
84.
hc
2 ca
q 2 q q 0
y qe
ht
q ye
qe
84
85.
q y eq y e
y e
y e
2
y e
y e
y ( 1 )y 0
2
1 1
1
85
86.
1.1
1
2
2
y y 0
0 :
1 соб
2
соб 1
*
соб
.
2
1
соб
2
*
соб
86
87.
q cоб q 0y y 0
2
2
q Aco s( ct ) y Y cos( )
q ye
Y e
cos( )
q0 hq0
Y A q0
*
c
2
2
87
88.
Как меняютсяt 0
0
y q e
Из
q0 q0
q q c
y
y qe
y0 q0
y0 q0 q0
q e
q0
q0
88
89.
q0 0,1 м q0 2 м / сек,Пример:
0,2
q0
2
q0
0,2 м
соб 10
соб 10с
1
y0 q0 q0 0,2 0,1 0,2 0,22 м
89
90.
q hq2
0
0
Y A q0
соб 1 2
Подставляя в:
q0 q0 c
y0 q0 q0
q0 q0
y0
2
Y A
2
2
y0
y
2
0
90
2
91.
q0 h q0tg *
соб q0
q0 h q0 соб
y0
Иначе:
2
y0
соб 1 q0
y C1 cos C2 sin
y C1 sin C2 cos
C1 Y cos , C2 Y sin
0 : C1 y0
C2
y0
y0
tg
y0
91
92.
9293.
Второй случай1
y (1 )y 0
2
1 k 0
2
2
y k y 0 k 0
2
2
2
y e
1, 2 k
k
k
y C1 e C2 e
k
k
y
k
C
e
k
C
1
2e
(3 a, б)
93
94.
Напоминание:y qe
y q e
y0 q0
q e
y0 q0 q0
y0 C1 C2
y0 k C1 k C2
Решая, которую
94
95.
Получим:k y0 y0 k y0 y0
C2
C1
2k
2k
q0 2 q0
C1
1 2
.
q0 1q0
C2
2 1
Эти были поучены ранее из размерного УД
95
96.
Подставляя в С_1 и С_2 корни1,2 соб 1
и учитывая
2
.
НУ:
y0 q0 q0
k y0 y0
C1
2k
y0 q0 и
получим
k y0 y0
C2
2k
96
97.
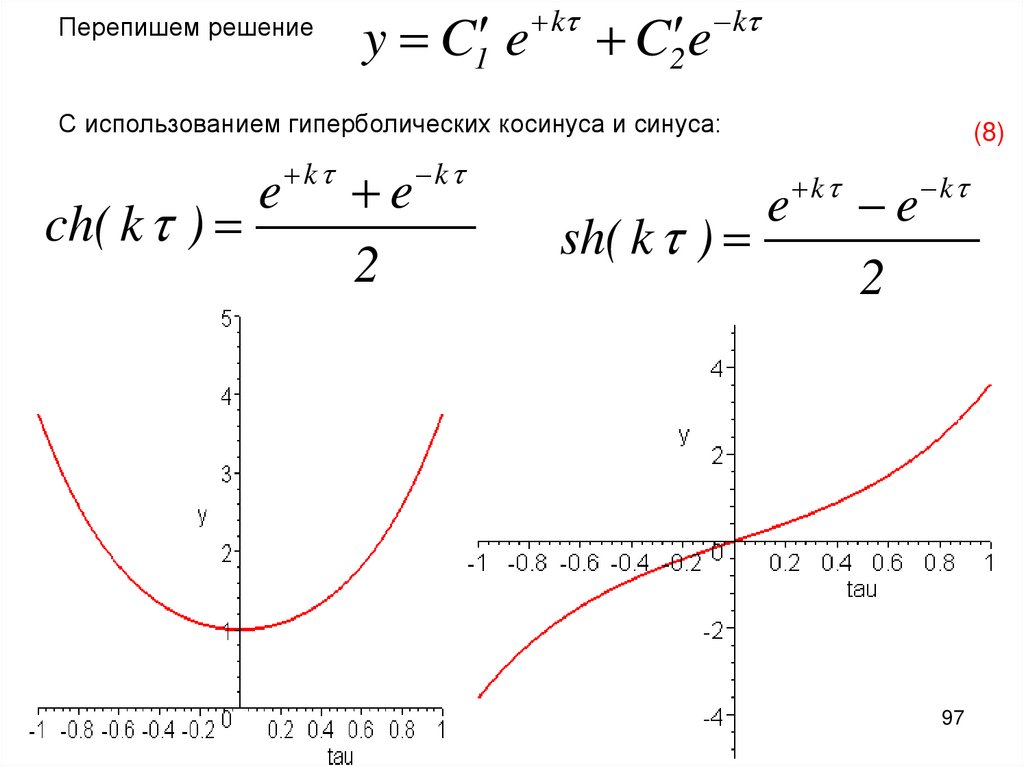
Перепишем решениеy C1 e
k
C2 e
k
С использованием гиперболических косинуса и синуса:
ch( k )
e
k
e
2
k
sh( k )
(8)
e
k
e
2
k
97
98.
Решая (8)e
e
k
Заменяя в решении
k
ch( k ) sh( k )
ch( k ) sh( k )
k
k
y C1 e C2 e
Экспоненты на..
y C1 ch k sh k
C2 ch k sh k
Или:
y C1 C2 ch k
C1 C2 sh k
98
99.
Вводя новые постоянныеC1 C1 C2 y0
y0
C2 C1 C2
k
y C1 ch k C2 sh k
Вводя новые постоянные:
C2 A sh
C1 A ch
И учитывая соотношения:
ch sh 1
ch ch ch sh sh
2
2
y A ch k
Получим окончательно:
(*)
99
100.
В котором новые постоянные:A C C
2
1
2
2
y0
y0
k
2
2
y0
C2
th
C1
ky0
решение (*) имеет такой же вид
как для колебательной системы
с заменой обычного косинуса на..
гиперболический
100
101.
Сводка результатов1
1
2
2
y y 0 y k y 0
y Ay cos( )
y Ay ch k
101
102.
Ayy0
y0
2
2
y0
Ay y0
k
2
2
y0
tg
y0
y0
th
ky0
102
103.
Частота1
Параметр
k
1
2
2
q ye
Вернёмся к
в которую подставим
y C1 e
k
q C1 e
C2 e
( k )
k
C2 e
( k )
Получим:
103
104.
104105.
Т.к.и
k 1
2
k 0
Вернёмся к случаю:
1
q Ae
y A
k
0
, то
Поэтому реш.
апериод.
И рассмотрим постоянные времени
y qe
q
y
105
106.
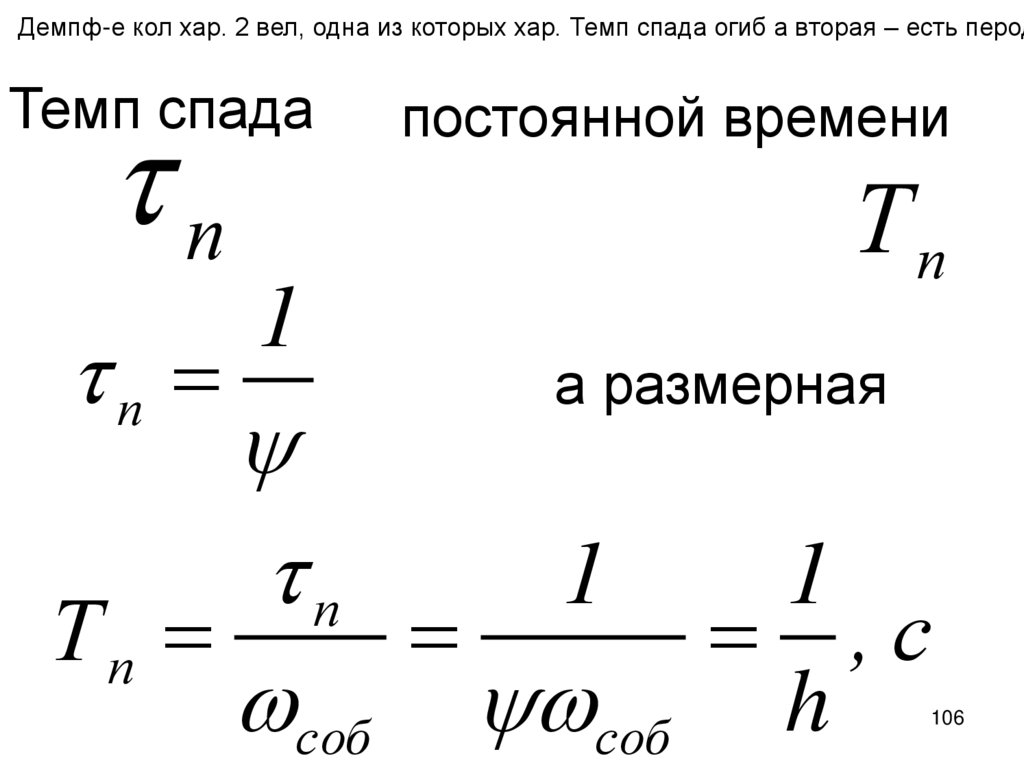
Демпф-е кол хар. 2 вел, одна из которых хар. Темп спада огиб а вторая – есть перодп
Темп спада
п
1
постоянной времени
Тп
а размерная
п
1
1
Тп
,с
соб соб h
106
107.
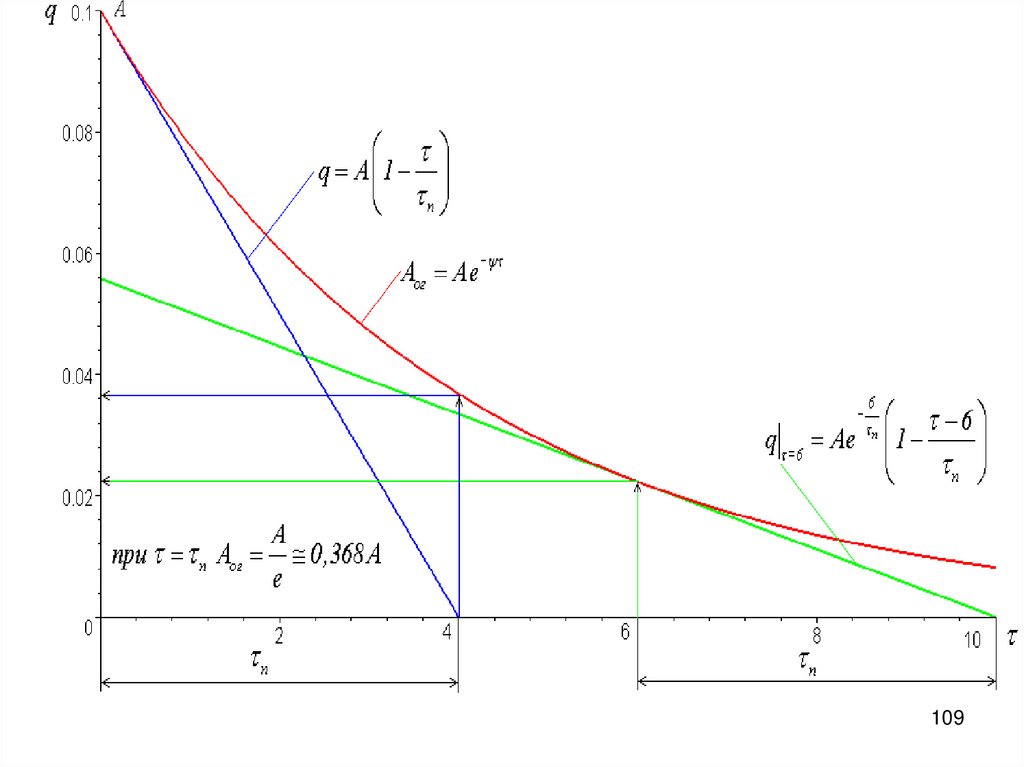
выражение для огибающейAог Ae
п
п
геометрический смысл
Производная
При
0
Aог
A
п
e
п
Угловой касательной
107
108.
Aог 0A
п
Уравнение касательной в нуле
q A 1
п
Пересекает ось тау в точке тау_п
п
e
1
0,368
e
108
109.
109110.
Общее уравнение касательной к огибающей в произвольной точке имеет вид:q Ae
*
п
1
п
*
Передемпфированный осциллятор характеризуется 2 пост вр:
1
1
п ,1
и п ,2
k
k
Пример на 2 пост вр передемпф осц:
110
111.
111112.
112113.
113114.
касательная к произвольной точкеп
*
q Ae
1
п ,1
k
1
п
*
п ,2
1
k
114
115.
Собственные частоты и формыколебаний консервативных систем
с конечным числом степеней свободы
d T
dt q j
T
П
q
q
j
j
П q1 ..qn
115
116.
П( q1 ,q2 ,...,qn ) П( 0,...,0 )П
1
П
qk
q j qk
2! j 1 k 1 q j qk
k 1 qk 0
n
n
n
2
0
1
П
qk q j qm ...
3! k 1 j 1 m 1 qk q j qm
n
n
n
3
0
116
117.
..Весьма громоздко даже для 2-х степеней свободы.Пример:
П
П q1 ,q2 П 0,0
q1
2
1 П
2
2 q1
П
q1
q2
q1 0
q2 0
q1 0
q2 0
q2
П
П
2
2
q1 2
q1q2
q2
2
q1 q2 q1 0
q2 q1 0
q1 0
q2 0
q2 0
q2 0
2
2
117
118.
31 П
3
3! q1
П
q 3 2
q1 q2
q1 0
3
3
1
q2 0
q1 0
q2 0
2
1 2
П
П
2
3
3
q
q
q
...
1
2
2
2
3
q1 q2 q1 0
q2 q1 0
q2 0
q2 0
3
3
118
119.
П 0,0..0 0Как и для сист с 1 ст св..:
П
П 0,0,..,0
k 1 qk
n
Теперь, при рассм задачи в лин постановке...:
0
qk 0
1
П( q1 ..qn ) c jk q j qk
2 j ,k 1
n
П
cjk
q j qk
2
- Обобщ коэф-ты жёсткости
c j k ck j
Максвелл и Бетти...:
q j 0
qk 0
119
120.
Пример:Найти коэф-ты жёсткости для системы:
При выборе в кач обобщ к-т абс перемещений..:
120
121.
12
П q1 ,q2 c1q1
2
1
2
2
c0 ,1
q1 l1 l1 S0 ,1
2
1
2
c2 q2 q1
2
1
2
2
c0 ,2
q2 l2 l2 S0 ,2
2
2
2
121
122.
Сразу видно, что П составлена для типично нелинейной системы,и для нахождения
с jk
П надо представить в виде
1
П( q1 ,q2 )
2
c
2
j ,k 1
jk
q j qk
1
c11q1q1 c12 q1q2 c21q2 q1 c22 q2 q2
2
(*)
122
123.
mtaylor П q1 ,q2 , q1 0, q2 0 , 4S0,1
1
П q1 ,q2 c1 c2 c0,1 q1q1
2
l1
c2 q1q2 c2 q2 q1
(**)
S0,2
c2 c0,2
q2 q2
l
2
123
124.
c11 c1 c2 c0 ,1c12 c2
S0 ,1
l1
c21 c2
c2 2 c2 c0 ,2
S0 ,2
l2
124
125.
c11 c12C c c
21 22
S0 ,1
c
c
c
c
2
1 2 0 ,1 l
1
S0 ,2
c2
c2 c0 ,2
l
2
125
126.
c0 ,1 c0 ,2 S0 ,1 0S0 ,2 0
Если...относительные перемещения
1 2
П q1,отн ,q2,отн с1q1,отн
2
2
1
2
2
с0 ,1 q1,отн l1 l1 S0 ,1
2
1
2
c2 q2,отн
2
2
2
1
2
с0 ,2 q1,отн q2,отн l2 l2 S0 ,2
2
126
127.
mtaylorc11 c12
C c c
22
21
S0 ,1
S0 ,2
c
c
c
1
0
,1
0 ,2
l1
l2
S0 ,2
c0 ,2
l2
c0 ,2
l2
S0 ,2
c2 c0 ,2
l2
S0 ,2
127
128.
c11...
C ci1
...
cn1
... c1 j
...
... ci j
...
... cn j
... c1n
...
... ci n
...
... cn n
128
129.
В МКЭ...:Pi ci ,1 ..
..ci j
..cin j
Pi ci ,1 1 .. ci j j .. cin n
129
130.
С исп МЖ..1
П q1 ..qn
2
c
n
j ,k 1
jk
q j qk
Записывается в виде:
1 T
П q1 ..qn q C q
2
130
131.
Лекция 3 ноября 2016г.131
132.
T q1 ..qn ,q1 ..qn1
2
2
2
A11 q1 A22 q2 .. An n qn
2
2A12 q1q2 .. 2A n 1 n q n 1 qn
Ai j Ai , j Ai , j q1 ..qn
a
jk
a j k ak j M
В этом сл ..
Ряд Маклорена
132
133.
Пример.a j k 1 2
133
134.
J C ,1J C ,2
T 1 , 2 , 1 , 2
1
2
2
2
J c ,1 M 1 1 b1 R1 2b1 R1 cos 1 1
2
1
2
2
2
J c ,2 M 1 2 b2 R2 2b2 R2 cos 2 2
2
mtaylor 1,0 0 2,0 0
134
135.
a11M
a21
a12
a22
J C ,1 M ,1 b1 R1
0
Если
bi 0 :
2
2
J C ,2 M ,2 b2 R2
0
3 M ,1
M 0
2
0
M ,2
135
В общем случае при рассм. малых колебаний:
136.
В общем сл при рассм малых кол выр д кин эн..., в кот М - ММасс1
Т a jk q j qk
2 j ,k 1
a11 ...
...
M ai1 ...
...
an1 ...
n
1 T
T q M q
2
a1 j
...
aij
...
anj
... a1n
...
... ain
...
... ann
136
137.
Об уст МС с кон ч ст св....Критерий Сильвестра:
c11 0 ,
c11
c12
c21
c22
0,
c11
c12
c13
c21
c22
c23 0 ,...,
c31
c32
c33
c11
...
c1n
...
...
cn 1
...
... 0.
cnn
137
138.
Эти усл аналог кр У д конс сист с 1 ст св, для У кот по Ляпунову необ и дост, чтс_экв>0
сэкв с0 l mgl сэкв с0 l mgl
2
И всегда..
сэкв 0
2
mg c0 l
сэкв 0
Отр. жёсткость
138
139.
1.3.2. Уравнения движенияконсервативных систем
с конечным числом
степеней свободы
139
140.
a j1q1 a j 2 q2 ... a jn qnc j1q1 c j 2 q2 ... c jn qn 0
j 1..n
M q C q 0
(*)
Пример составления уравнений
системы с двумя степенями свободы:
140
141.
141142.
T( q1 ,q2 ,q1 ,q2 )1
A11 q1q1 2A12 q1q2
2
2
2
m1q1 m2 q2
2
A22 q2
2
2
142
143.
Т.к. – абс перем и распр масса пружин не учитыв, то перекр произв в Т не будетq1q2 0 q2 q1 0
Поэтому:
A21 0
A11 m1
от
A2 2 m2
q1 q 2
A12 0
, и матрица масс принимает вид
m1
M 0
.
0
m2
143
144.
Кинетическая энергия записываетсяв виде
1
T q1 ,q2
q M q
Т
2
m1
1
q1 q2
2
0
0 q1
.
m2 q2
Найдём производные:
d T
q1
П
C
M
q
;
q2
q
dt
q
j
144
145.
j 1,2 Система уравнений движениM q C q 0
В развёрн. виде:
m1
0
0 q1
m2 q2
S0 ,1
c1 c2 c0 ,1 l
1
c2
c2
q
1
0
S0 ,2 q2
c2 c0 ,2
l2
145
146.
S0 ,1m1 q1 c1 c2 c0 ,1
q1 c2 q2 0
l1
m q c q c c S0 ,2 q 0
2 2 2 1 2 0 ,2 l 2
2
S0 ,1 S0 ,2 0
:
m1 q1 c1 q1 c2 ( q2 q1 ) 0
(*)
m2 q2 c2 ( q2 q1 ) 0
146
147.
Каждое из ур содержит по одному ускорению и обе обобщ к-ты.Уравнения взаимосвязаны, и интегрировать их надо совместно.
Если добавить ещё одну третью массу
справа, то система уравнений
примет вид:
147
148.
m1 q1 c1 q1 c2 ( q2 q1 ) 0m2 q2 c2 ( q2 q1 ) c3 ( q3 q2 ) 0
m q c ( q q ) 0
2
3 3 3 3
Рассм ур имеют по одному инерц члену , т.к. Т имеет канон вид:
148
149.
Нет перекр члqi q j
А есть только..
2
i
q
Т.е.:
n
1 T
1
2
Т q M q ak qk
2
2 k 1
Канон вид.. Абс перем и пренебр массами пружин
149
150.
Отн.перем.
масс:
m1 m2 q1,отн q1
q2,отн q2 q1
S0 ,1 S0 ,2 0
В пренебр
массами пруж:
Ур движ:
c1 0
C 0 c
2
m1 m2
M
m
2
m2
m2
150
151.
m1 m2m
2
m2 q1,отн c1 0 q1,отн
0
m2 q2,отн 0 c2 q2,отн
m1 m2 q1,отн m2 q2,отн c1q1,отн 0
(**)
m
q
m
q
c
q
0
2 2,отн
2 2,отн
2 1,отн
Сод по одной обобщ к-те и все обобщ ускорения.
Следствие того, что канон вид имеет пот эн
151
152.
n1
1
T
2
П q1 ,q2 qотн C qотн ck qk ,отн
2
2 k 1
Путём использования:
q1,отн q1 q2,отн q2 q1
свести..
152
153.
При выборе.. абс. перем..n
a j q j с jk qk 0
k 1
При выборе.. отн. перем..:
n
a
k 1
jk
qk с j q j 0
153
154.
(НКМС-2006, с. 53) Канонический вид..n
1
2
П c j j
2 j 1
n
1
2
T a j j (*)
2 j 1
Блок 4, тоже 1 ст. св…:
Такой вид имеют Т и П для системы с
ОДНОЙ ст. свободы.
Это означает, что движение МС с n ст. св.
происходит точно также, как и движение системы
с 1 ст. св., а именно: по гармоническому закону.
154
155.
Такая возм-ть выделения чисто гарм. режимаобусловлена линейностью..,
допускающей частное решение вида
q j i Aj i cos ci i
Начальные условия.. ,напр., перемещения .. ,
а скорости =0.
Распадаются на..:
ai i ci i 0
i 0
2
c,i i
Координаты
i
наз. нормальными или главными
координатами
155
156.
РЕШЕНИЕ СУ УРАВНЕНИЙ ДВИЖЕНИЯ (с. 54)Частное решение однородной системы
M q C q 0
имеет вид:
q j Aj cos c
j - cт свободы
156
157.
Решение системы уравнений движенияM q C q 0
q j Aj e
Aj
i c t
c и
i 1
qj
Эксп. возр. или убыв. множитель..
Это привело бы к изменению..Е
Частное
решение
E T П
q j Aj cos( c t ).
Подставив это решение в систему .., получим в развёрнутом виде:
(1.95)
157
158.
( a11 A1 ... a1n An )(
c
A
...
c
A
)
0,
1n
n
11 1
: ..
2 ( a A ... a A )
c
n1
1
nn
n
( cn1 A1 ... cnn An ) 0.
2
c
158
159.
( c11 a ) ... ( c1n a ) A1:
..
:
..
:
..
0
( cn1 c2 an1 ) ... ( cnn c2 ann ) An
2
c 11
2
c 1n
Для того, чтобы система имела ненулевое решение, необходимо,,
c11 a
2
c 11
... c1n a
2
c 1n
(1.95а)
(1.96)
0.
cn1 a
2
c n1
... cn n a
2
c nn
159
160.
Развернув определитель, получим уравнение частот, или ХУb0 b1 ... ( 1) bn
2
c
bi
полож
n
2
с
2n
c
0
..вещ и положительны..
...
2
c1
2
c2
2
cn
q j i Aj i cos( c it i ),
160
161.
Общее решение:n
n
q j q j i Aj i cos( c i t i ).
i 1
(1.97)
i 1
161
162.
Постоянныеn
:
Aj i
i
q q0 j
0j
Собственные формы колебаний
1.
2.
c,i
n 1
3.
Это значит, что разыскив. ампл.:
n
Aj i A1 i
162
163.
A1i1i
1
A1i
n( n 1)
A2i
2i
A1i
ni
c i
q j q j i A1,i j i cos c ,it i
n
i 1
Ani
A1i
n
i 1
(1.98)
163
164.
Пример.S0 ,1 S0 ,2 0
c1 c2 c0
m1 m2 m0
164
165.
2c0 m0c0
2
c
A1
0
2
c0 m0 c A2
c0
165
166.
20
2
0
c0 2 c
c 3 c
0
m0
m
4
Число
2
c ,1
2
c ,2
5
3 5 c0
c0
0,382
2 m0
m0
3 5 c0
c0
2,618
2 m0
m0
иррационально, поэтому движение по кажд ст cвободы
будет непериодическим
166
167.
Продолжим.. Подставляя частоту.. В сист ур отн амплитуд167
168.
3 52
A11 A21 0
2
3 5
A
1
A
0
11
21
2
Или приближённо:
1,618 A11 A21 0
A11 0,618 A21 0
2
c ,2
168
169.
A11A21
A11 5см
11
1
A11 5см
A21 1,618 5см
21
1,618
A11
5см
A12 6см
12
1
A12 6см
A22 0,618 6см
22
0,618
A12
6см
169
170.
170171.
Ортогональность собственныхформ колебаний
В СЛАУ..
( c11 a ) ... ( c1n a ) A1
:
..
:
..
:
..
0
( cn1 c2 an1 ) ... ( cnn c2 ann ) An
2
c 11
2
c 1n
Вместо амплитуд можно подставить .. Тогда
C M 0
2
c
171
172.
C M 02
ci
i
Такая запись означает, что система совершает
чисто гарм. режим движения с вполне определ.
отношениями МЕЖДУ ампл., опр-ми св-ми
системы
q0 , j 0
q0 , j Задать
При ПРОИЗВ. Н.У...
,
i
проп коэф собствненных форм
A1,i
НАХОДЯТСЯ..И3 РЕШЕНИЯ..И ЕГО ПРОИЗВОДНЫХ ПРИ
t 0
172
173.
t 0n
q j 0 j i A1,i cos i
i 1
n
q j 0 ji A1,i c ,i sin i
i 1
ДЛЯ ПРОИЗВ. i-го ТОНА сист. ур. отн. амплитуд:
C M 0
2
c ,i
i
(1.100)
j
T
(*)
j C i j M i 0
T
2
c ,i
T
173
(1.101)
174.
Умножаяна
систему слева
ПОЛУЧИМ:
Повтор для сравнения:
j
T
j C i j M i 0
T
2
c ,i
T
(*)
Умножая.. записанную для
C M
2
c, j
j
j го тона
0
слева
и
транспонируя
её,
на i
получим
(**)
T
T
2
j C i c , j j M i 0
T
174
175.
C CT
Вычитая из
(*)
(**)
0
T
j M i 0
2
c, j
и учитывая
2
c ,i
(103)
Подставляя это соотн. в: ..
(**)
j C i j M i 0
T
получим
2
c ,i
T
j C i
T
0
(104)
175
176.
энергия.. по..Физически..
i
-ой форме
..........................................................................................
На перемещениях масс по
j
-ой форме
..работа сил инерции.. .равна нулю .
Умножая
C M 0
i
C
2
i
i
c ,i
T
i M i
2
c ,i
i
T
на
получим
176
177.
iПоскольку коэф-ты соб форм изв с точн до пост множителя, то всегда можно
n
найти
чисел
умножив на которые коэф-ты соб форм:
i i i
*
можно обратить знаменатель выражения для частоты в единицу:
i i M i i 1
T
Отсюда
i
.
1
i M i
T
177
178.
iнормирующие множители
i
* нормированные коэффициенты
собственных форм
Даже при безразмерных ..
i
*
i
становятся размерными.
i C i
С их использованием...
, а решение
n
n
q j q ji A1,i
i 1
*T
2
c ,i
i 1
*
ji
*
cos c ,i t i
178
179.
Пример проверки ортогональностисобственных частот и форм колебаний
179
180.
2c01 1,618
c0
c0 1
c0 0,618
2,618
c0 1 1,618
1,618
c0 2,618 2,618 0
180
181.
m01 1,618
0
0 1
m0 0.618
0
m0 1 1,618
0,618
m0 1 1 0
Найдём
Нормирующие множители:
181
182.
11
m0
1 1,618
0
1
, кг
3,618m0
2
0 1
m0 1,618
1
2
1
m0
1 0,618
0
1
, кг
1,382m0
1
2
0 1
m0 0,618
Конец примера
182
183.
Соотношения ортогональности с использованием соб форм записываютсяв виде
j M i
*T
*
j C i
*T
*
0, если i j
1, если i j
0,
если
i
j
2
,
если
i
j
c
,i
183
184.
Нормальные (главные) координатыЭто такие координаты, для которых движение при любых Н.У., будет
одночастотным и гармоническим.
n
n
q j q ji A1,i
*
ji
cos c ,i t i
i A1,i cos c ,it i
i 1
qj
i 1
Заменяется
i
n
qj
i 1
*
ji i
q j j1 1 j 2 2 .. j n n
*
*
*
184
185.
q*
*
..
*
: : :
*
*
n1 .. nn
*
11
*
1n
185
186.
qИз
i
*
(*)
q
* 1
:
*
Обратная к
Подстановка (*) в систему уравнений
движения даёт:
M C 0
*
*
*T
M C 0
*T
*
*T
*
186
187.
E 02
E
c
2
c
0
2
c
0
0
2
c ,1
0
2
c ,2
0
0
0
0 0
.. 0
2
0 c ,n
0
187
188.
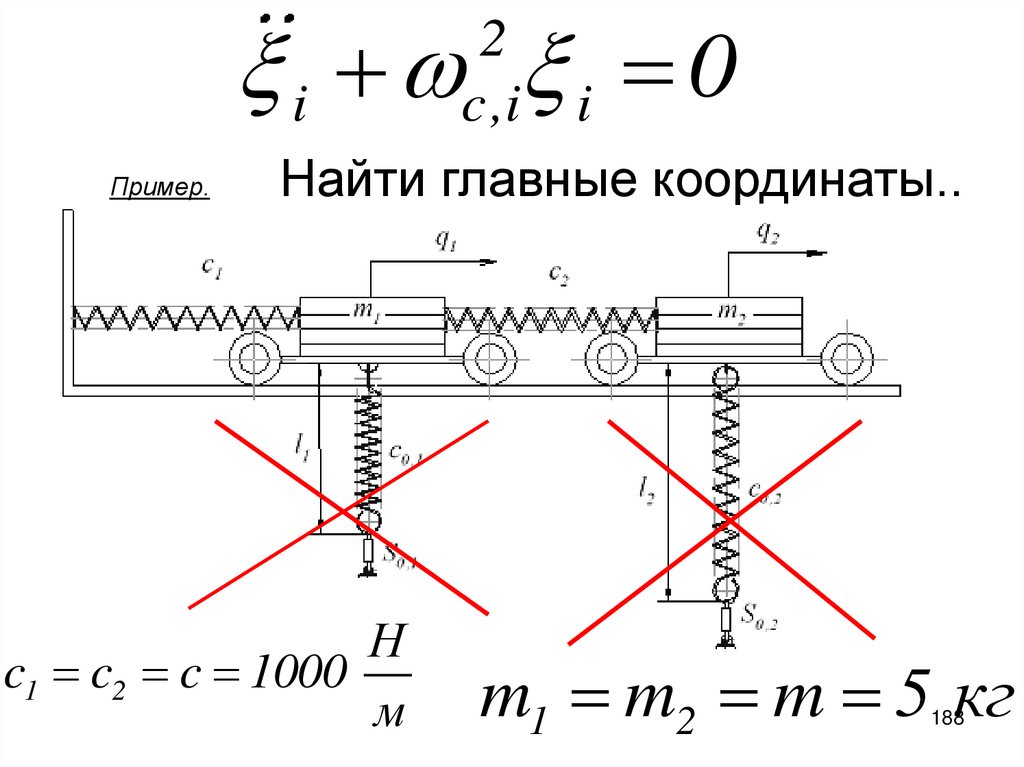
0Пример.
2
i
c,i i
Найти главные координаты..
Н
c1 c2 c 1000
м
m1 m2 m 5 кг
188
189.
приt 0 :
q1 0 q1, 0 0,05 м
м
q1 0 q1,0 0
сек
q2 0 q2, 0 0,05 м
q2 0 q2,0
м
сек
3- 5 c
-1
c,1=
8,740320492 c
2 m
3+ 5 c
-1
c,2=
22,88245611c
2 m
189
190.
Решение для координатqj
имеет вид
q1 A11 cos c ,1 t 1 A12 cos c ,2 t 2
*
11
*
12
q2 A11 cos c ,1 t 1 A12 cos c ,2 t 2
*
21
,.
*
22
Из выражений для скоростей в начальный момент времени
q1,0 A11 c,1 sin 1 A12 c,2 sin 2 0
*
11
*
12
q2,0 A11 c,1 sin 1 A12 c,2 sin 2 0
*
21
*
22
190
191.
следует, что1 2 0
Тогда из выражений для перемещений в начальный момент
времени получим систему линейных уравнений относительно неизвестных амплиту
A11
и
A12
A A q1,0
A A q2,0
*
11 11
*
11 21
*
12 12
.
*
12 22
С учётом выражений для нормирующих множителей
1
1
, кг
3,618m0
1
2
1
2
, кг
1,382m0
191
1
2
192.
1 0,235115205 кг1
2
2 0,3804226068 кг
1
2
1 2
1 1
1,618 1 0,618 2
1
0,2351141011 0,3804226068
0,3804226068 -0,2351141008 кг 2
*
192
193.
Решив с помощью команды linsolve систему двух линейных уравнений, получимA11 0,1538841768
A12 0,03632712638
м кг
м кг
Выражения для обобщённых координат примут вид (рис. 1.22)
q1 (t)=A11 cos c ,1 t+A12 cos c ,2 t
*
11
*
12
0,036 cos 8,74 t+0,014 cos 22,88 t
q2 (t)=A11 cos c ,1 t+A12 cos c ,2 t
*
21
*
22
0,059 cos 8,74 t - 0,009 cos22,88 t
193
1
2
1
2
194.
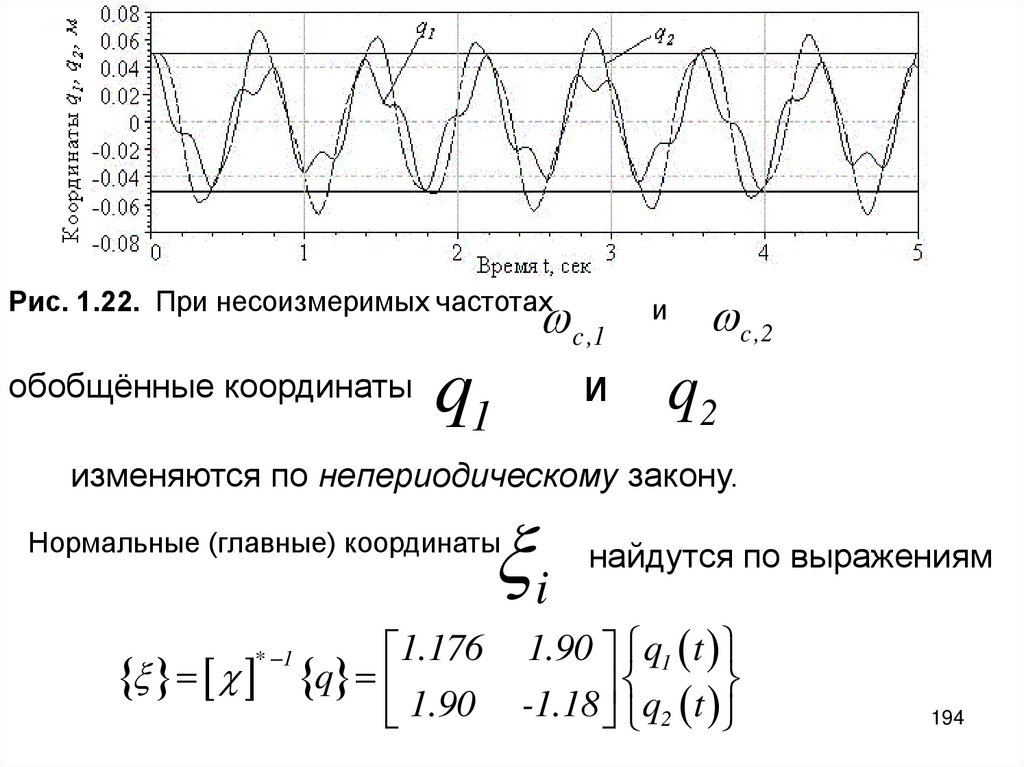
c ,1Рис. 1.22. При несоизмеримых частотах
обобщённые координаты
q1
и
и
c ,2
q2
изменяются по непериодическому закону.
i
Нормальные (главные) координаты
* 1
найдутся по выражениям
1.176 1.90 q1 t
q
1.90 -1.18 q2 t
194
195.
* 1в которых матрица
находится при помощи команды inverse пакета linalg
q1
q1
и
q2
и
q2
Нормальные координаты 1
и
2
Рис. 1.23 НКМС-2006.
Частоты те же, но
режимы периодические
– это такие координаты, которые в соответствии с линейными дифференциальными
уравнениями
изменяются по гармоническому закону;
при этом первоначально выбранные координаты
изменяются по непериодическому закону.
195
196.
В развёрнутом виде выражения для нормальных координат принимают вид1 t 0,154 cos(8,74 t)+0,2 10
-10
cos(22,88 t)
2 t 0,6 10 -10 cos(8,74 t)+0,036 cos(22,88 t)
(Частоты те же, что и при выборе первоначальных координат)
Эти гармонические колебания происходят не одновременно!!
Это колебания двух разных систем с 1 степенью свободы.
Жёсткости и коэффициенты инерции могут быть любыми,
но так, чтобы их отношения
196
равнялись бы квадратам соб частот
197.
Lсeq c c3
R3
3
1
a M M1 M3
8
2
q 3 R3
1 2 2 1 2 2
П cR3 3 c3 L 3
2
2
.
2
L 2
c c3 2 R3
R3
2
ceq ,3
2
3
R
197
198.
q 3 R31 2 2
T aR3 3
2
3
1
2
2
a3 aR3 M M 1 M 3 R3
8
2
2
2
ceq, 3 ceq R3
a aR
Т.е.
и
3
3
.
.
M обода
GJ p
Lторс
3
1
M M1 M3
8
2
сR c3 L
2
3
2
Jp
M диска
32
3
1
2 M M1 M3
8
2
4
торс
D
198
199.
JpD
32
4
нар
D
4
внтр
199
200.
Роль начальных условийq j Aj r cos c r t r
j 1,2..,n
200
201.
Вынужденные колебанияd T T П
Q t
dt q q q
aq cq Q t
201
202.
m LT
2
2
mgL
П
2
2
mL mgL F t L
2
Q t F t L
202
203.
m x LT
2
2
mgL
П
2
2
F t 0
x
mL mgL 0
L
2
или
mL mgL mLx
2
203
204.
Q t mLx-- вынуждающий момент переносной силы инерции.
здесь относительная координата;
-- переносная
xДействие
гармонической вынуждающей силы
на линейную систему с 1 степенью свободы
без трения
F t AF cos t
Mq cq F t
Ms
2
c q s F s
204
205.
q s q t e dtst
0
q s
1
W s
2
F s c Ms
s i
i 1
q i
1
W i
2
F i c M
205
206.
1W i
2
c M
AF
A
c
c
1
c 1 2
c
2
A
AF
1
2
1
AF
qст
с
206
207.
207208.
2Из ЧХ
1
1
W i
2
c M
1
c 1 2
c
следует, что ФЧХ – сдвиг фазы между
q
2
A
AF
F
и силой
колебаниями
равен нулю, т.к. мнимая часть равна нулю
Re
0
arctg
arctg
0
2
0
Re
в дорезонансе и
208
в зарезонансе.
209.
При1
1
колебания происх в фазе с силой, а в зарезонансе в противофазе.
Состояние системы
1
209
называется резонансом
210.
Уравнение движения в этом случаеAF
q q
cos c t
M
2
c
Его решение при нулевых н.у.:
AF
q
t c cos ct sin ct
2c
В решении появился вековой, или резонансный член:
t c cos c t
, который неограниченно возрастает во времени.
В реальных системах силы трения ограничивают
210
бесконечное нарастание колебаний.
211.
ЕслиAF k
2
, где к для машин с неуравновешенным ротором
, М – масса ротора, r – его эксцентриситет, то:
A
2
k a 1
2
k M рот r
AF M рот r k
2
2
211
212.
212213.
Действие кинематического гармонического возмущенияна линейную систему с 1 степенью свободы с трением
Уравнения движения линейных осцилляторов
с одной степенью свободы
213
214.
При использовании безразмерного собственноговремени системы
соб t t
, представляющего собой растянутое или сжатое в соответствии с собственной частотой
214 время
, производные от обобщённых координат и возмущения записываются в виде
215.
q q собx x соб
dq
q
d
dx
x
d
q q
2
соб
x x
2
соб
2
d q
q 2
d
2
d x
x 2
d
215
216.
Схема а).aq ( q x ) cq 0
a q соб q cq соб x
2
соб
2 ca
q 2 q q 2 x
216
217.
AWq x
x0
qотн q x
2
1
2 2
4
2
2
2 qотн
qотн x x
qотн
Aотн
Wqотн x
x0
1
1
2 2
2
4
2
2
217
218.
АЧХ абсолютных перемещений при возмущении за демпфер218
219.
АЧХ относительных перемещений при возмущении за демпфер219
220.
Схема б).aq q c q x 0
q 2 q q x
2 qотн
qотн
qотн
x 2 x
A
Wq x
x0
1
1
2
2
4
2
2
220
221.
x t221
222.
4Aотн
Wqотн x
x0
2 2
2 2
1
4
2
2
2
2
222
223.
Aqx0
АЧХ абсолютных перемещений при возмущении за пружину
A
Wq x
x0
1
1
2 2
4 2 2
223
224.
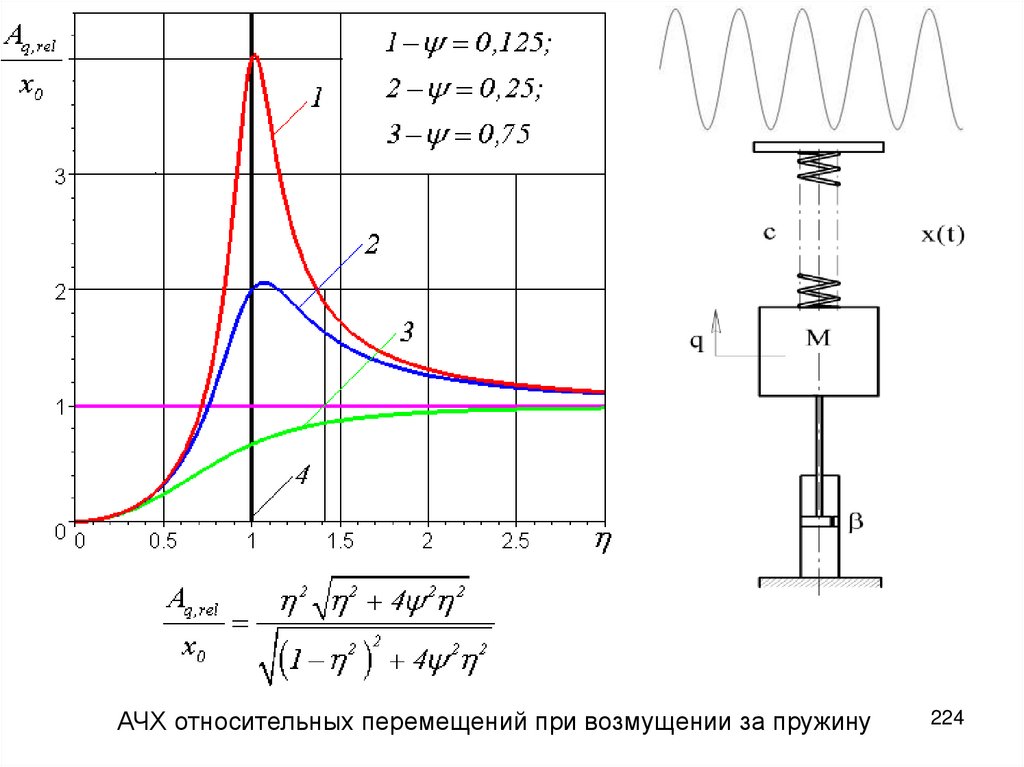
АЧХ относительных перемещений при возмущении за пружину224
225.
Схема в).Здесь следует заметить, что применять принцип
суперпозиции
для схемы в) на основании результатов по схемам а) и б)
можно только для абсолютных перемещений,
а для относительных нельзя, потому что они для
схем а) и б)
различные, а абсолютное – одно и то же.
225
226.
Возмущения, прикладываемые к концам демпфера и пружины в схемаха) и б) раздельно,
в схеме в) действуют одновременно.
Поскольку все эти модели линейные, но различные, то результат действия
возмущения в схеме в) по абсолютным перемещениям
можно получить, суммируя результаты действия возмущений
в предыдущих схемах а) и б)
q 2 q q x 2 x
в относительных координатах
aq ( q x ) c q x 0
226
227.
2 qотнqотн x
qотн
A
Wq x
x0
A
Wq , отн x
x0
1 4
2
1
2
2
1
2
4
2
2
2
2 2
4
2
2
Размерности слагаемых в уравнениях движения в собственном времени
системы, пропорциональные инерционным, диссипативным и силам,
227
зависящим от времени, имеют размерности не сил или моментов, а
размерность соответствующей обобщённой координаты.
228.
АЧХ абсолютных перемещений при возмущении за пружину и демпфер228
229.
АЧХ относительных перемещений при возмущении за пружину и демпфер229230.
Aqqст
2
tg
2
1
q e
ht
C
qст
1
1
2 2
4
2
4
2
2
H
qст
с
sin t C2 cos t
*
соб
1
2 2
1
*
соб
cos t
2
230
231.
Процесс установления колебаний зависит от соотношения частотвынуждающей силы и собственной
Отношения
Aq
qст
Arel
x0
наз коэффициентами
динамичности
Максимумы АЧХ вида
Aq
qст
A
x0
Arel
x0
1
1
2 2
4
2
1
1
2 2
1
4 2 2
2
при силовом возмущении
с пост ампл силы;
при кинематическом возмущении за пружину,
2
2 2
4
2
2
при кинематическом возмущении в схеме в
231
232.
при малом линейном трении незначительно смещаются влево или вправоот скелетной вертикали
1
Поэтому на практике
рез
1
2
рез
определяют по приближённой формуле
2
рез
При квадратичной зависимости амплитуды силового возмущения от частоты,
.
АЧХ такой системы
Aq
k a
1
2
2 2
4
2
2
232
233.
233234.
Сила на основание при параллельном соединении..R q cq
R qотн cqотн
234
235.
Устойчивость состояний равновесия иавтоколебания.
Устойчивость состояний равновесия.
В разделе «Св. колебаний» уже касались вопросов
устойчивости состояний
равновесия систем без притока энергии и около
положений равновесия.
Продолжим рассмотрение автономных систем
с притоком энергии.
Рассмотрим несколько задач.
235
236.
В каждой из них выделяется один параметр,от которого зависит устойчивость и
неустойчивость состояния равновесия
(неподвижной точки).
Задача состоит в нахождении критического
Значения этого параметра, при котором устойчивость
сменяется неустойчивостью.
236
237.
Будем рассматривать только линейные задачи, т. е. малые отклонения системыот состояния равновесия.
Этого достаточно для того, чтобы судить о тенденциях возмущённого движения и
тем самым вынести суждение об устойчивости или неустойчивости в «малом».
Системы с 1 ст. свободы. Задача 1.
Рассматриваются вопросы устойчивости систем с одной степенью свободы,
связанные с аэроупругой неустойчивостью типа дивергенции.
237
238.
Пластинка жесткая и тонкая, упруго опертая слева и шарнирно справа,вектор потока воздуха
параллелен пластинке в её невозмущённом состоянии,
в котором подъемная сил равна нулю, а лобовым сопротивлением
пластинки как следствием весьма малого трения можно пренебречь.
Пластинка в равновесии под действием её веса и реакций опор.
Найти критическую скорость потока.
При отклонении пластины возникают аэродинамические давления,
зависящие от угла отклонения
лобовое сопротивление и подъёмная
сила
/
X сx ql ;
Y c y ql
ρ
q
2
2
238
Размер пластинки, перпендикулярный рисунку, принят равным единице
239.
Положение центра давления (расстояние) считаем независимым от угла φ.
b
Пренебрегая моментом от лобового соприкосновения, напишем
уравнение движения
как баланс моментов при отклонении пластины от состояния равновесия
J + co L - c y
2
2
2
Lb 0
J + co L - c y
b L 0
2
2
Условие устойчивости записывается в виде:
2col
кр
c y ρb
b 0
co L c y
239
2
Выражение (1.1) определяет скорость дивергенции.
2
240.
Задачи этого типа относятся к теории аэрогидроупругостиПример 2. Отрицательное трение
Рассмотренные ранее диссипативные силы,
направлены против скорости, эти силы демпфируют колебания.
В некоторых МС возникают силы, такие зависящие от скорости, но совпадающие
с ними по направлению.
Такие силы, оказывая дестабилизирующее действие,
раскачивают систему; и такие силы называют силами «отрицательного трения».
Формально:
aq q cq 0
c
h ; ω ;
2c
a
2
c
ω ω h q 2hq ω q 0;
*
c
2
c
2
2
c
240
241.
Корни Х.У.λ 1,2
Если
2 4ac
2a
1
q e
ht
h h ω соб i 1
2
2
c
2
, то корни оказываются оба комплексно сопряжёнными
с положительной вещественной частью.
Тогда решение пишется в виде
q0 hq0
*
*
sin
t
q
cos
t
c
0
c
*
c
При сколь угодно малых начальных возмущениях
q0
и
q0
возникнут колебания, амплитуды которых будут возрастать по экспоненте.
Состояние равновесия оказывается неустойчивым:
241
242.
Состоянию равновесия соответствует особая точка типанеустойчивый фокус (ψ<1)
242
243.
и неустойчивый узел (ψ>1).Конкретный пример такой МС,
в которой при колебаниях может возникнуть сила отрицательного трения
243
244.
Барабан 3 прижат к телу 1 и вращается с постоянной угловой скоростью.Между барабаном и телом действует сила сухого трения R,
характеристика которой показана на рис
В отличие от обычной схематизации, эта характеристика отражает реальное влияние
скорости скольжения на силу трения. В первом квадранте характеристика состоит из
двух участков: падающего при
0
*
и возрастающего при
*
244
245.
0– это скорость скольжения при неподвижной тележке.
Ей соответствует сила
R0
При этом пружины сжаты на величину
R0
q0
;
c
q
Теперь движение тележки около этого состояния равновесия. Обозначим через
дополнительное перемещение тела. Скорость скольжения найдётся как разность
Скорость скольжения перестает быть постоянной величиной, найдётся как разность
0 q
которая будет определять уже переменную силу трения R.
При малых колебаниях, когда
q 0
можно принять:
245
246.
R R0 R0 q;или
dR
R0
d 0
mq R c q0 q 0
mq R0 R0 q c q0 q 0
mq R0 q cq 0
246
247.
ПриПри
*
*
R0 0 и колебания будут затухать
R0 0
и после сколь угодно малого возмущения в системе происходит
самовозбуждение колебаний.
При
0
*
0
состояние равновесия устойчиво. При
*
неустойчиво.
Это решение (в малом) определяет лишь тенденцию к нарастанию колеба
С ростом амплитуды представление
R R 0 R0 q
становится всё менее точным. Необходимо учитывать нелинейность силы т
247
248.
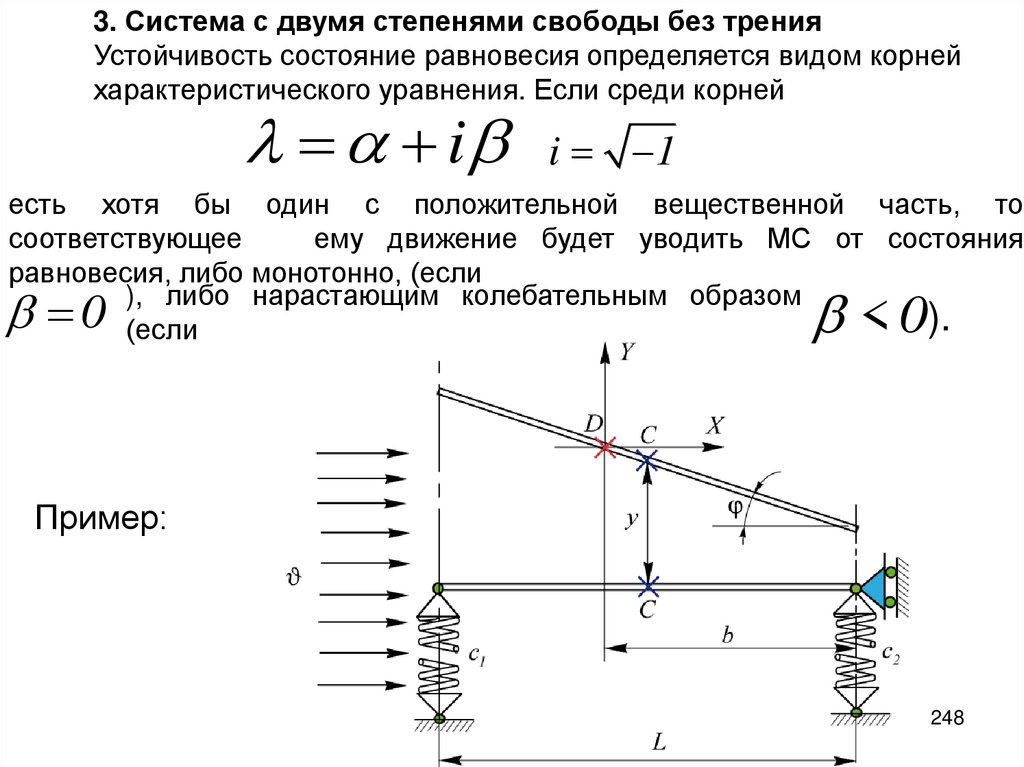
3. Система с двумя степенями свободы без тренияУстойчивость состояние равновесия определяется видом корней
характеристического уравнения. Если среди корней
i
i 1
есть хотя бы один с положительной вещественной часть, то
соответствующее
ему движение будет уводить МС от состояния
равновесия, либо монотонно, (если
), либо нарастающим колебательным образом
).
(если
0
<0
Пример:
248
249.
В отличие от шарнирного, упругое закрепление правого конца пластинысоздает ещё одну возможность возникновения неустойчивости,
обусловленную неконсервативными свойствами этой системы
с двумя степенями свободы
t
y t – смещение центра тяжести–иугол поворота пластинки.
Примем, что угол
положителен по часовой стрелке.
L
R1 c1 y
2
L
R2 c2 y
2
– реакции.
249
250.
Запишем дифференциальные уравнения движенияL
L
my c1 y 2 c2 y 2 c y qL 0
2
mL c y L L c y L L Y b L 0
1
2
12
2 2
2 2
2
Однородная система уравнений
y c11 y c12 0
c21 y c22 0
Коэффициенты в этой системе:
250
251.
c1 c2 c c L c y 2c11 c 1 2
L
12
m
m 2 m 2
6 c1 c2
c21
mL
cy q
3 c1 c2
c22
6
L
2b
2
m
mL
.
251
252.
Неравенствоc12 c21 является признаком неконсервативности системы
энергия этой системы может убывать с течением времени
при малых скоростях потоках и возрастать при больших.
Принимая частное решение в виде
A2 e ;
y A1e ;
λt
c11 λ
c21
λt
2
получим
A1
0
2
c22 λ A2
c12
.
Отсюда следует характеристическое уравнение
252
253.
c11 λ2
c21
c12
c22 λ
2
λ c11 c22 λ c11c22 c12c21 0
4
2
Корни этого ХУ имеют вид:
1,2 ,
3 ,4
2
c11 c22
c11 c22
c11c22 c12 c21
2
2
253
254.
Если разностьc11c22
– c12 c21 0
, то один из корней, соответствующий двум знакам плюс),
оказывается
вещественным
и
положительным.
Соответствующее
ему движение есть апериодический
монотонный уход от состояния
равновесия, которое
оказывается неустойчивым.
Если эта разность положительна и, кроме того,
c11 c22
c11c22 c12 c21
2
;
2
.
то корни
1 .. 4
оказываются комплексными:
254
255.
1 i2 i
4 i 3 i
где
положительные и вещественные.
и
Первой паре корней соответствует движение
y A11e A12e
λ1t
A21e A22e
λ1t
λ 2t
λ 2t
B1e sin t 1
αt
B2e sin t 2 ;
αt
255
256.
Это колебания с монотонно возрастающими амплитудами.Состояние равновесия системы в этом случае является неустойчивым.
Таким образом, чтобы система после возмущения оставалас
бы в окрестности состояния статического равновесия
(признак устойчивости), необходимо, чтобы разность
c11c22 c12 c21
удовлетворяла бы двум неравенствам:
c11 c22
0 c11c22 c12c21
2
2
При нарушении первого равенства возникает дивергенция
256
257.
y(t), phi(t)При нарушении второго условия возникает флаттер
257
258.
Границам области устойчивости соответствуют знаки равенств вc11 c22
0 c11c22 c12c21
2
Если подставить в (*) выражения для
2
(*)
ci j
, то найдём 2 критических значения скорости, которая является
параметром, определяющим устойчивость:
скорость дивергенции:
div
2c1c2 L
c y c1 b L c2b
скорость флаттера:
258
259.
flut1 c c1c2 c
2
;
3 c y
c1 c2
2
1
При малых жесткостях правой опоры, когда
2
2
L
c2 c1 1
b
div оказывается мнимой, т. е. дивергенция невозможна
Если наоборот, жесткость левой опоры меньше жесткости
правой, то скорость
flut
– мнимая, флаттер невозможен.
Флаттер – это реальная опасность для многих
конструкций в потоке жидкости или газа
(лопатки турбины, крыло самолёта, обшивка259
ЛА).





















































































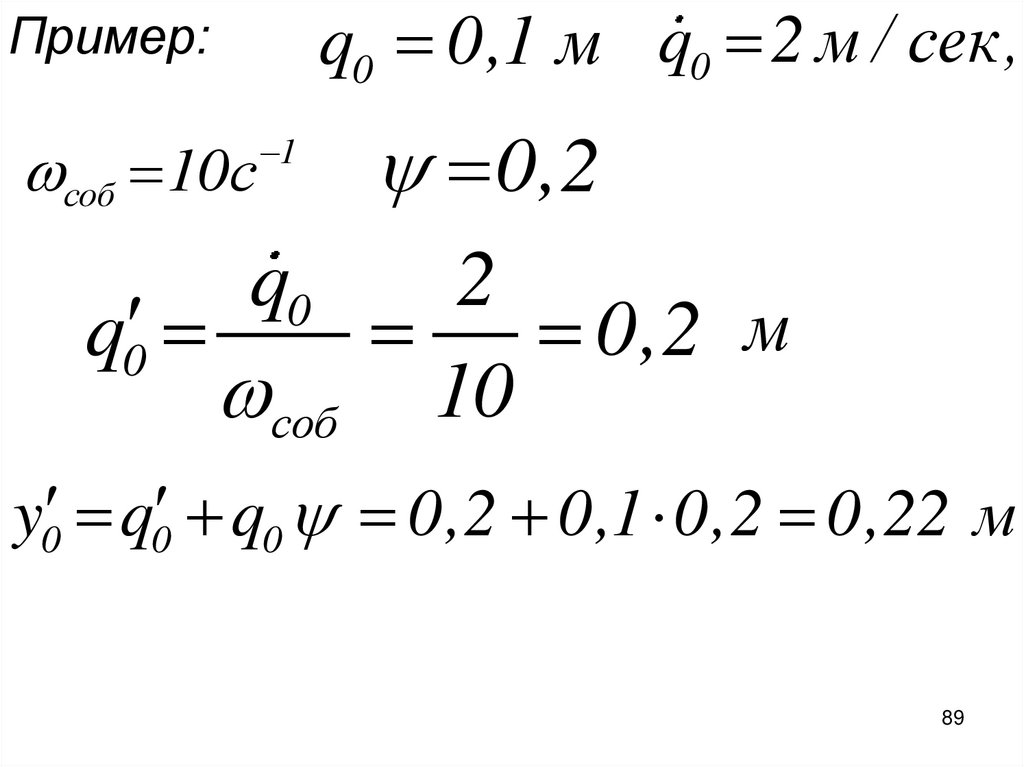








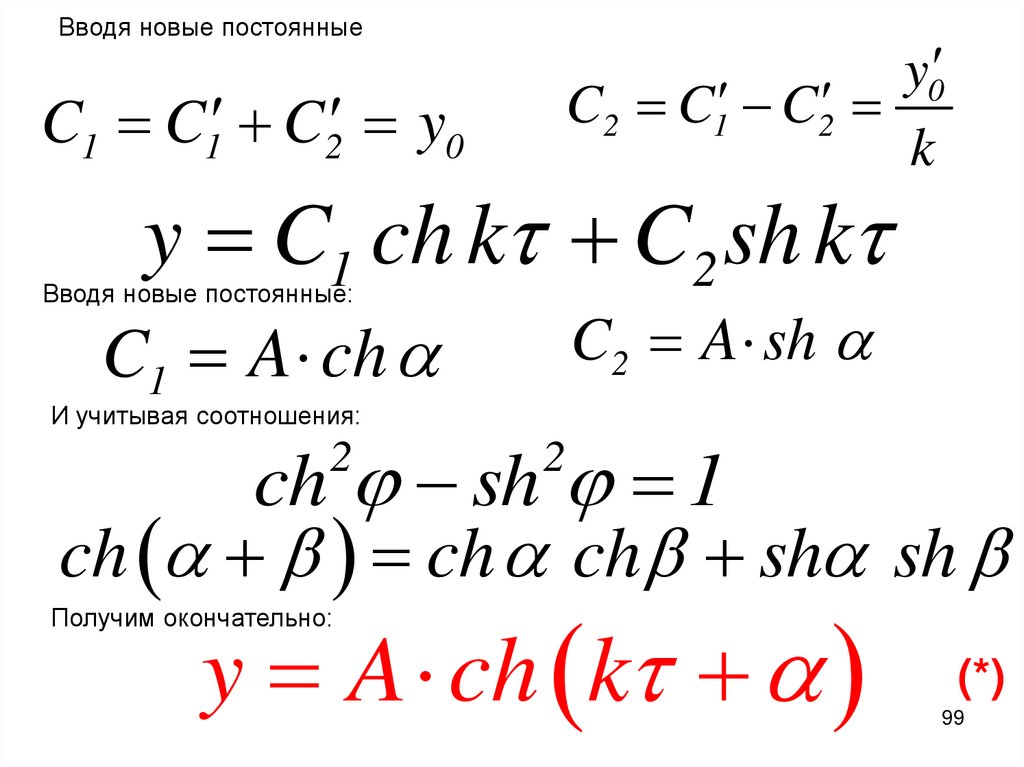











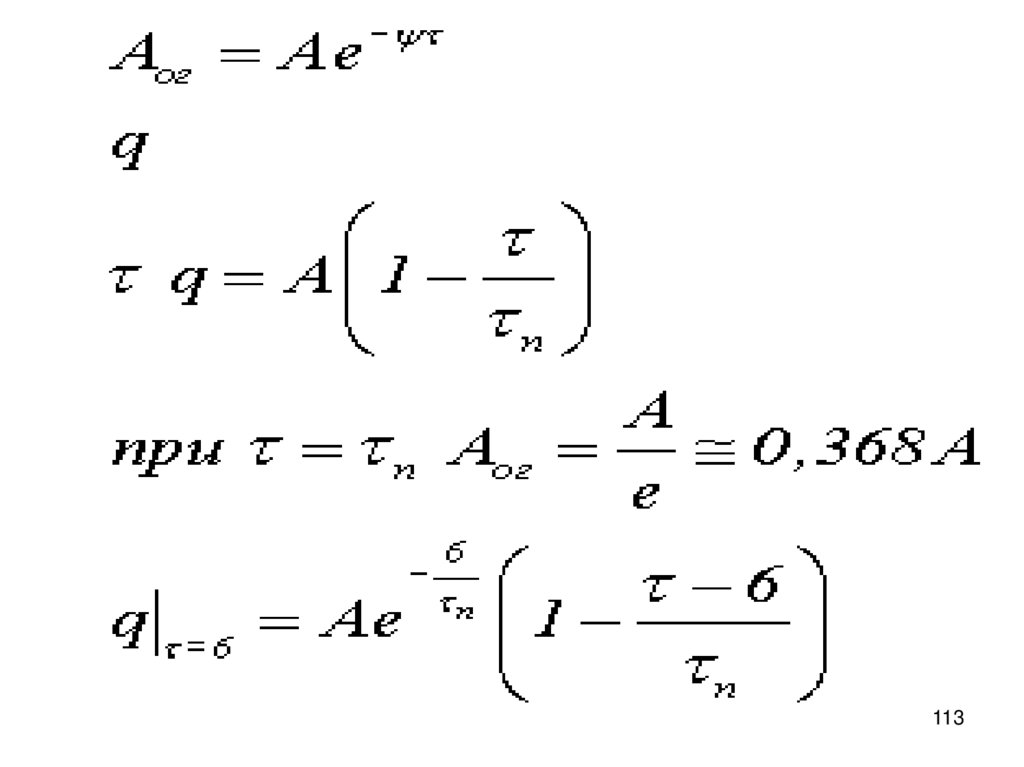




























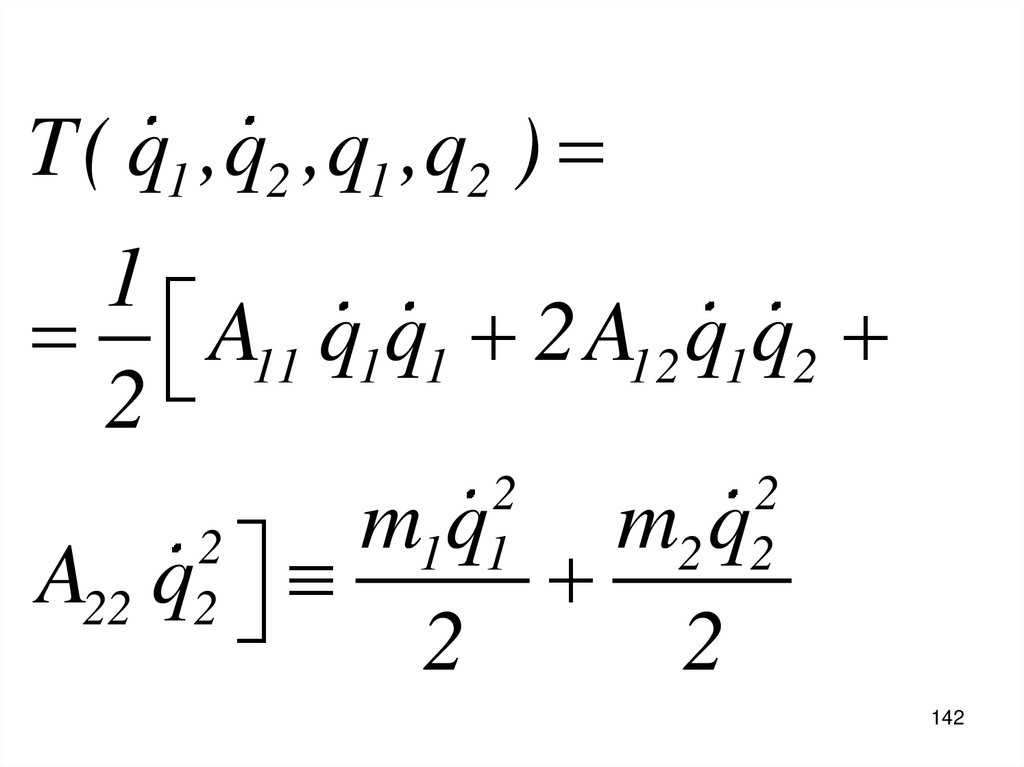





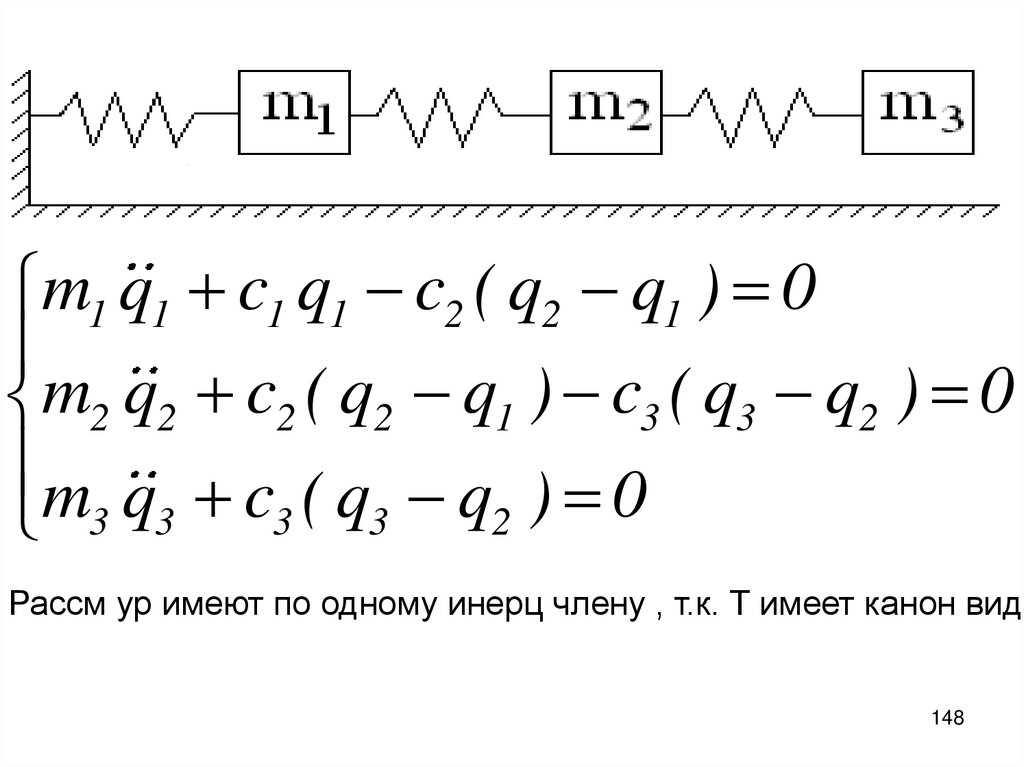
























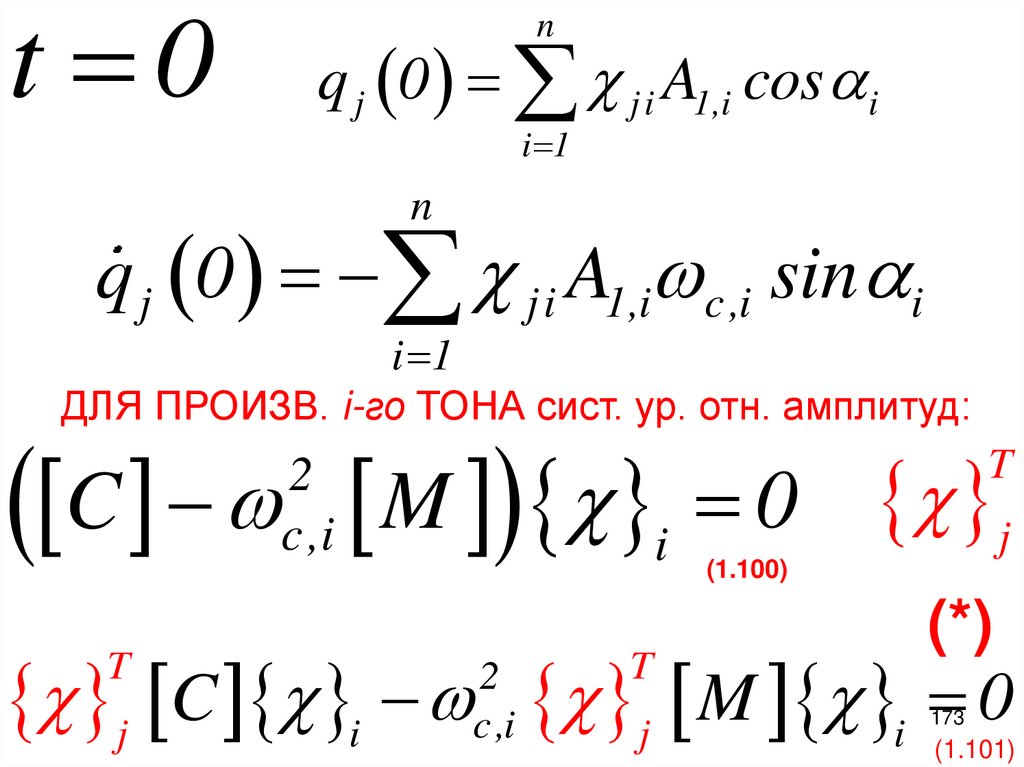













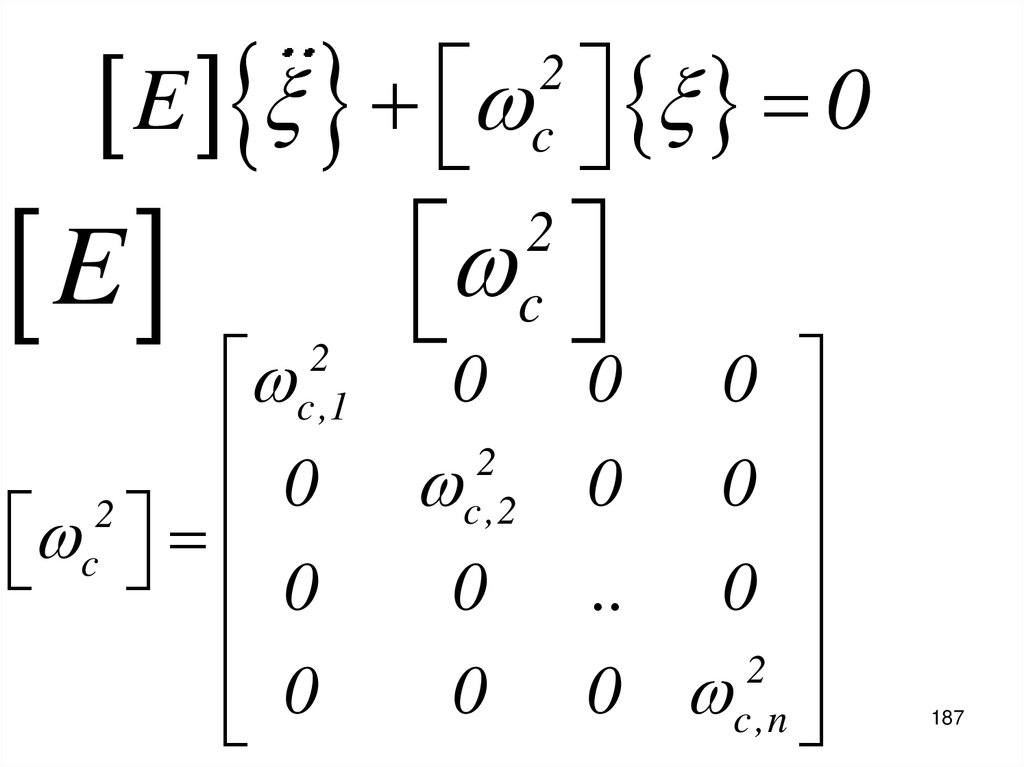
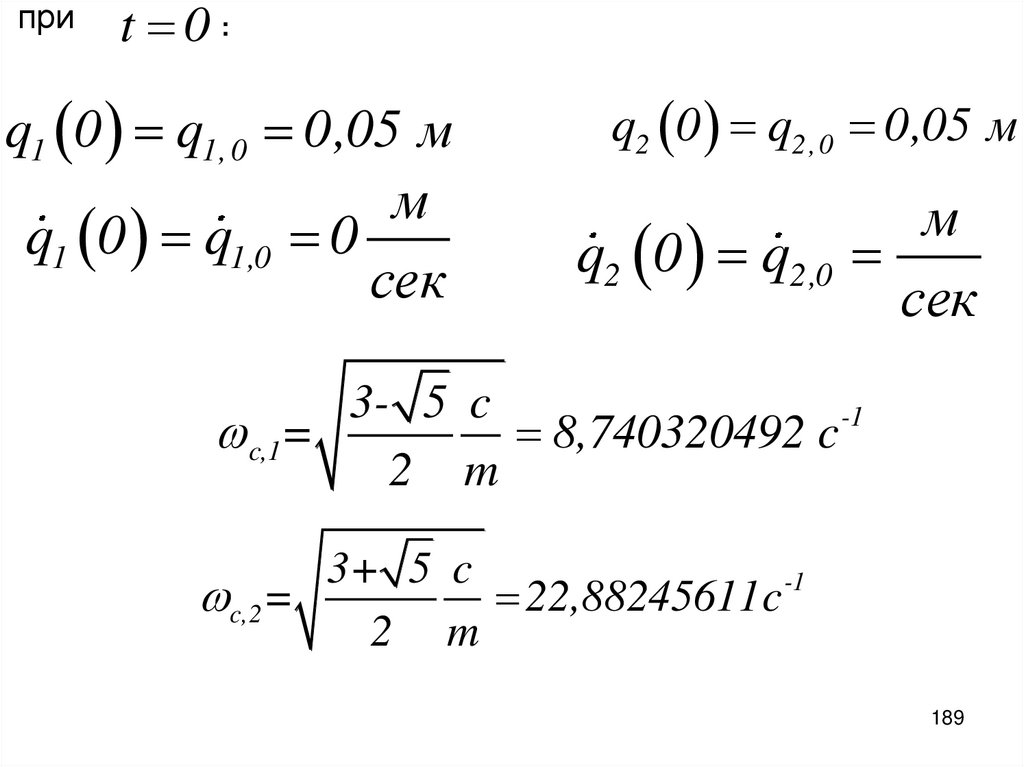












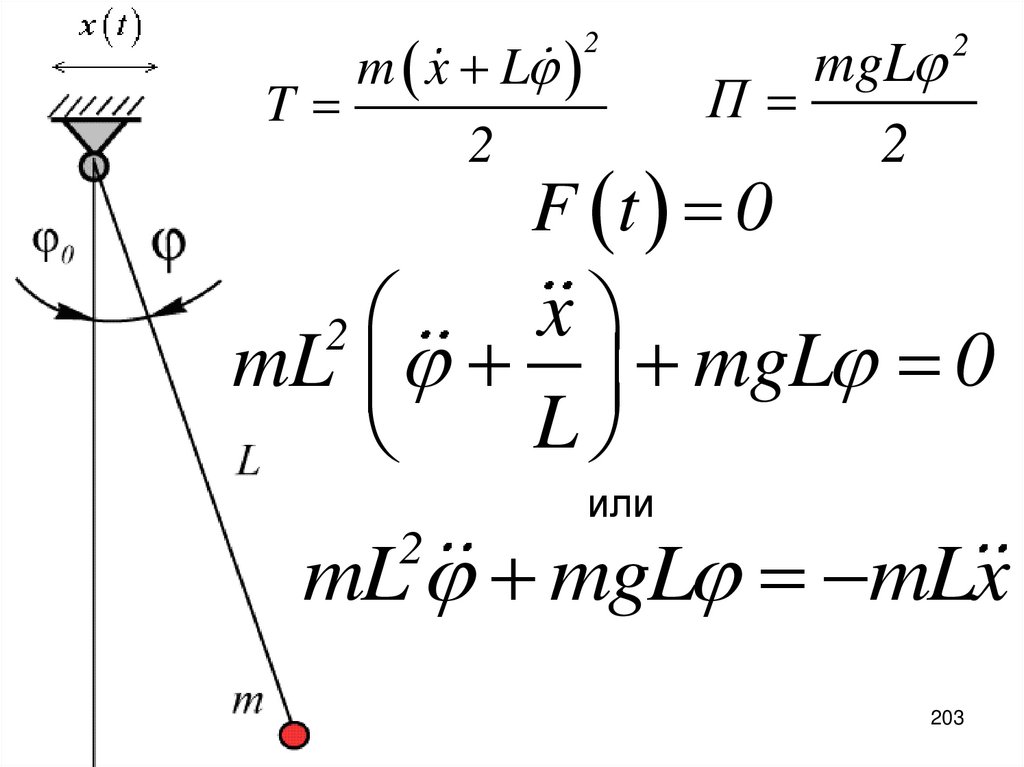


















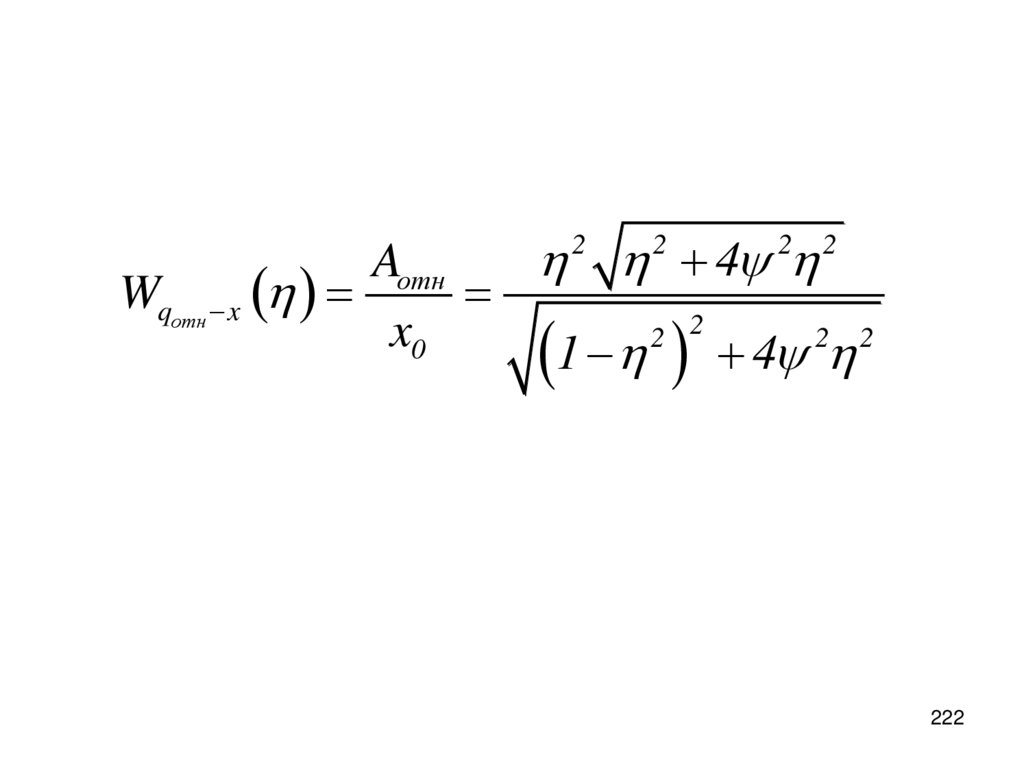



































 Математика
Математика








