Похожие презентации:
Метод вариации произвольных постоянных. (Лекция 2.12)
1. Лекция 2-12. 12.3.6. Метод вариации произвольных постоянных.
Дано линейное дифференциальное уравнениеy¢¢ + a1 ( x ) y¢ + a2 ( x ) y = f ( x ) ,
где
f ( x ) - непрерывная функция.
y = yooчн+ u .
(*)
Рассмотрим однородное уравнение
y¢¢ + a1 ( x ) y¢ + a2 ( x ) y = 0.
Общее решение данного уравнения имеет вид
yoo = C1 y1 + C2 y2 .
Будем искать частное решение уравнения (*) в виде
uчн = C1 ( x ) y1 + C2 ( x ) y2 .
2. Далее везде примем обозначение
C1 ( x ) = C1, C2 ( x ) = C2 .¢ = C1¢ y1 + C2¢ y2 + C1 y1¢ + C2 y2¢ .
uчн = C1 ( x ) y1 + C2 ( x ) y2 . uчн
Т.к. определению подлежат две функции C1 ( x ) , C2 ( x ) ,
то одним соотношением между ними распорядимся
произвольно. Наиболее целесообразно подчинить
¢ = C1 y1¢ + C2 y2¢ ,
условию C1¢ y1 + C2¢ y2 = 0. Тогда uчн
¢ , uчн
¢¢ в
¢¢ = C1¢ y1¢ + C1 y1¢¢ + C2¢ y2¢ + C2 y2¢¢ . Подставим uчн , uчн
uчн
уравнение (*)
C1¢ y1¢ + C1 y1¢¢ + C2¢ y2¢ + C2 y2¢¢ + a1C1 y1¢ + a1C2 y2¢ + a2C1 y1 + a2C2 y2 =
= C ¢ y¢ + C ¢ y¢ + C y ¢¢ + a y ¢ + a y + C y ¢¢ + a y ¢ + a y = f ( x ) ,
1 1
2 2
1
(
1
1 1
2 1
)
C1¢ y1¢ + C2¢ y2¢ = f ( x ) .
2
(
2
1 2
2 2
)
Получили систему дифференциальных уравнений
для определения
C1 ( x ) , C2 ( x ) .
3.
{C1¢ y1 + C2¢ y2 = 0,
C1¢ y1¢ + C2¢ y2¢ = f ( x ) .
y1 y2
y1¢ y2¢
¹ 0.
4. Пример.
y¢¢ + y = tg x.y = yooчн+ u .
2
¢¢
y
+
y
=
0,
r
+ 1 = 0. r1,2 = ±i, a = 0, b = 1, s = 1.
yoo = C1 cos x + C2 sin x.
y1 = cos x, y2 = sin x.
uчн = C1 ( x ) cos x + C2 ( x ) sin x.
C1¢ cos x + C2¢ sin x = 0,
sin 2 x
C1¢ = , C2¢ = sin x.
-C1¢ sin x + C2¢ cos x = tg x.
cos x
2
sin x
1 ö
æ
æp xö
C1 = - ò
dx = ò ç cos x ÷ dx = sin x - ln tg ç + ÷ ,
cos x
cos x ø
è
è4 2ø
C2 = ò sin xdx = - cos x.
æ
æ p x öö
y = C1 cos x + C2 sin x + ç sin x - ln tg ç + ÷ ÷ cos x - cos x sin x,
è 4 2 øø
è
{
æp xö
y = C1 cos x + C2 sin x - ln tg ç + ÷ cos x.
è4 2ø
5. 12.3.7 Линейные дифференциальные уравнения -го порядка.
12.3.7 Линейные дифференциальныеуравнения n -го порядка.
Выше изложенное переносится на дифференциальные
уравнения порядка n > 2.
n)
n -1)
(
(
y + a1 ( x ) y
+ ... + an-1 ( x ) y¢ + an ( x ) y = f ( x ) , (**)
где a1 ( x ) ,..., an-1 ( x ) , an ( x ) , f ( x ) - непрерывные функции.
Сначала рассмотрим однородное уравнение
n)
n -1)
(
(
y + a1 ( x ) y
+ ... + an-1 ( x ) y¢ + an ( x ) y = 0. (***)
6. Линейно независимые системы функций.
Рассмотрим систему функций j1 ( x ) ,..., jn ( x ) .C1j1 ( x ) + ... + Cnjn ( x ) ,
Линейной комбинацией их будет
C1,...,
гдеCn
- постоянные.
Определение. Система функций j1 ( x ) ,..., jn ( x ) .
называется линейно независимой, если ни одну из этих
функций нельзя представить в виде линейной
комбинации остальных.
Т.е. не может быть равенства j1 ( x ) = C2j2 ( x ) + ... + Cnjn ( x ) .
В частности j1 ( x ) , j2 ( x ) линейно независимы, если
j2 ( x )
¹ const.
j1 ( x )
7. Если не есть линейно независимые функции, то они линейно зависимы.
Если j1 ( x ) ,..., jn ( x ) не есть линейно независимыефункции, то они линейно зависимы.
• Пример.
j1 ( x ) = x, j2 ( x ) = x 2 , j3 ( x ) = x 3 , j4 ( x ) = 2 x - x 2 .
j4 ( x ) = 2j1 ( x ) - j2 ( x ) .
8. Теорема.
Если y1,..., yn сутьnчастных линейно независимых
решений дифференциального уравнения (***), то общим
решением этого уравнения будет
(****)
y = C1 y1 + ... + Cn yn .
Если y ,..., y - линейно зависимые решения, то, по крайней
1 из nних выразится через остальные
мере, одно
и функция будет зависеть не от , а от
y
n решенияn - 1
n -1
произвольных
постоянных. Она не даст общего
дифференциального уравнения.
(
)
(
)
9.
• Условие линейной независимости частных решенийдифференциального уравнения
W ( y1, y2 ,..., yn ) =
y1
M
n -1)
(
y
1
K
O
L
yn
M ¹ 0, "x.
n -1
y( )
n
• Если заданы начальные условия
n -1
y x = x = y0 , y¢ x = x = y0¢ ,..., y ( )
0
0
x = x0
( n-1) ,
= y0
то, чтобы из общего решения yоо = C1 y1 + ... + Cn yn получить
частное решение , надо решить систему алгебраических
ìC y + ... + C y = y ,
уравнений
n n0
0
ï 1 10
í....................................
ïC y ( n-1) + ... + C y ( n-1) = y ( n-1) .
n n0
0
î 1 10
Здесь W0 ¹ 0.
Нулевым начальным условиям соответствует
C1 = C2 = ... = Cn = 0.
10.
• Линейно независимые решения дифференциальногоуравнения n - го порядка образуют фундаментальную
систему решений.
• Общее решение неоднородного дифференциального
уравнения
y = yooчн+ u .
11. Теорема.
Если y1,..., yn - фундаментальная система решенийдифференциального уравнения
n
n-1
y ( ) + a1 ( x ) y ( ) + ... + an-1 ( x ) y ¢ + an ( x ) y = 0,
то решением дифференциального уравнения
n
n -1
y ( ) + a1 ( x ) y ( ) + ... + an-1 ( x ) y ¢ + an ( x ) y = f ( x )
является функция C1 ( x ) y1 + ... + Cn ( x ) yn , где C1 ( x ) ,..., Cn ( x )
ìC1¢ y1 + ... + Cn¢ yn = 0,
удовлетворяют системе
ïC1¢ y1¢ + ... + Cn¢ yn¢ = 0,
í...............................
ï
( n-1) + ... + C ¢ y ( n-1) = f x .
¢
C
y
( )
n n
î 1 1
Определитель системы есть определитель Вронского.
12. 12.3.8 Линейные дифференциальные уравнения -го порядка с постоянными коэффициентами и правой частью специального вида.
n12.3.8 Линейные
дифференциальные
уравнения
-го порядка с постоянными
коэффициентами и правой частью
специального
n
nвида.
-1
y ( ) + a1 y ( ) + ... + an-1 y¢ + an y = 0.
Характеристическое уравнение
r n + a1r ( ) + ... + an-1r + an = 0.
1) Каждому действительному корню r кратности s
соответствует s решений e rx , xe rx ,..., x s -1e rx .
2) Каждой паре комплексно сопряженных корней r = a ± b i
кратности s соответствует sрешений
n -1
eax cos bx, xeax cos b x,..., x s -1eax cos bx,
eax sin b x, xeax sin bx,..., x s -1eax sin bx.
Общее число кратности равно n,поэтому решений будет
n.
13. Пример.
5)4)
(
(
y + y + 2 y¢¢¢ + 2 y¢¢ + y¢ + y = 0.
r 5 + r 4 + 2r 3 + 2r 2 + r + 1 = 0.
r1 = -1, r 4 + 2r 2 + 1 = 0.
r1 = -1, a = -1, b = 0, s = 1.
r2,3,4,5 = ±i, a = 0, b = 1, s = 2.
y = C1e
-x
+ ( C2 + C3 x ) cos x + ( C4 + C5 x ) sin x.
14. Рассмотрим неоднородное дифференциальное уравнение
nn -1
y ( ) + a1 y ( ) + ... + an-1 y ¢ + an y = f ( x ) ,
где
часть
f ( x ) = eax ( P1 ( x ) cos bx + P2 ( x ) sin- правая
bx )
специального вида,
P1 x - многочлен степени
- многочлен степени
P2 x решение имеет вид
Частное
( )
( )
m,
n.
k ax
u
=
x
e
R
x
cos
b
x
+
R
x
sin
b
x
,
(
)
(
)
(
)
чн
1
2
где
- многочлены степени
R1 ( x ) , R- 2кратность
l = max ( m, n ) ,
( x)
среди корней
r = a ± bi
характеристического
уравнения.
k


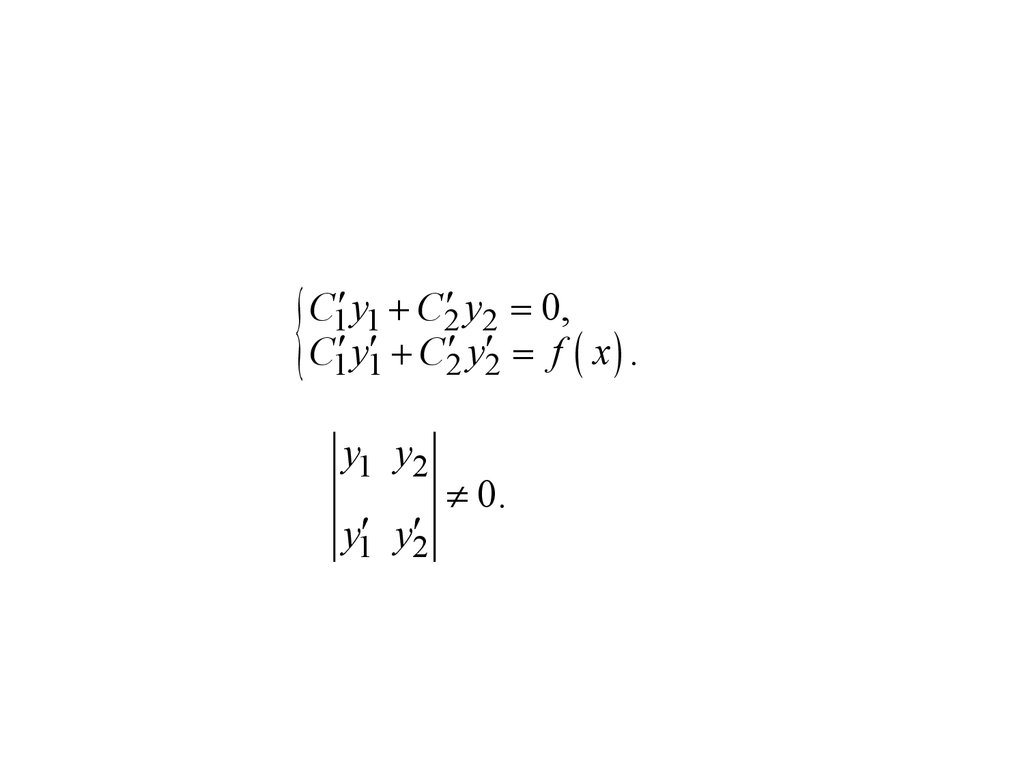











 Математика
Математика








