Похожие презентации:
Перевод чисел из десятичной системы счисления в любую другую
1. Перевод чисел из десятичной системы счисления в любую другую
2.
1. Что такое система счисления?2. Виды систем счисления? Примеры.
3. Что такое основание позиционной системы
счисления?
4. Как перевести число из любой системы
счисления в десятичную?
5. Существует ли число 1032?
6. Существует ли число 2788?
3.
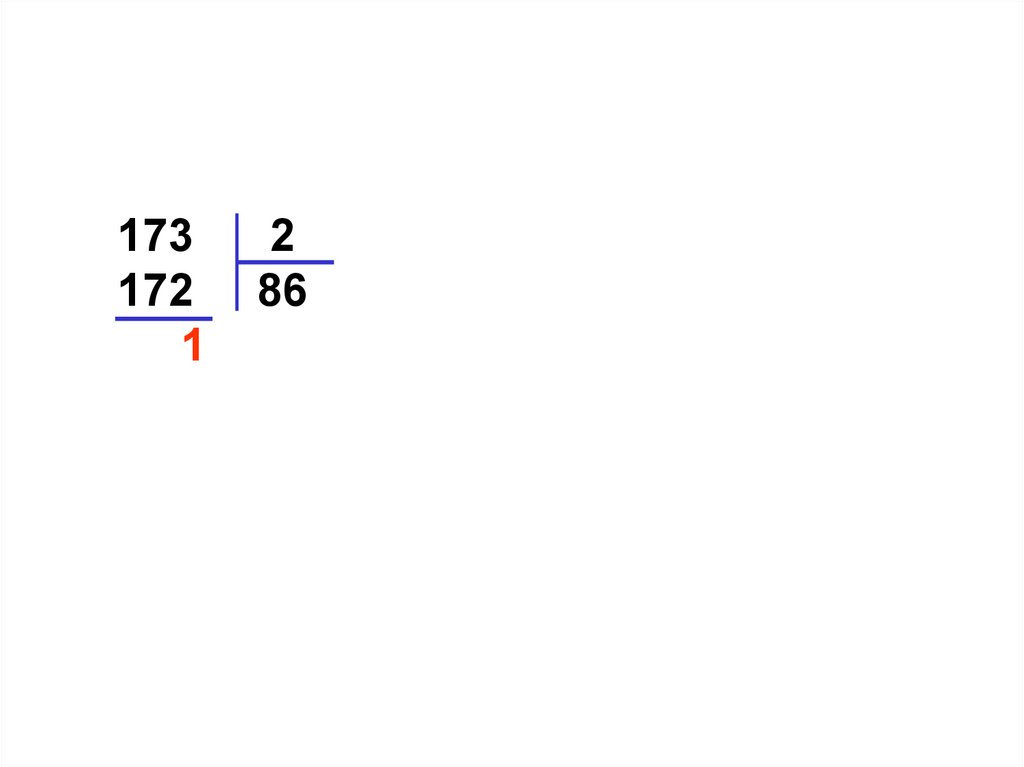
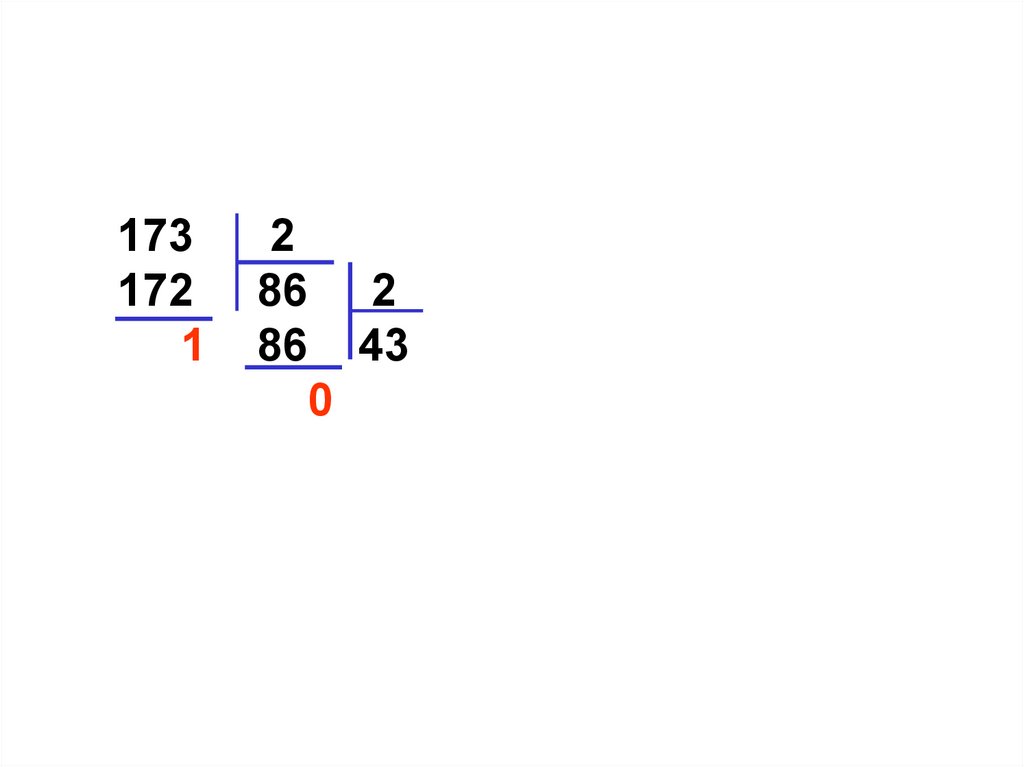
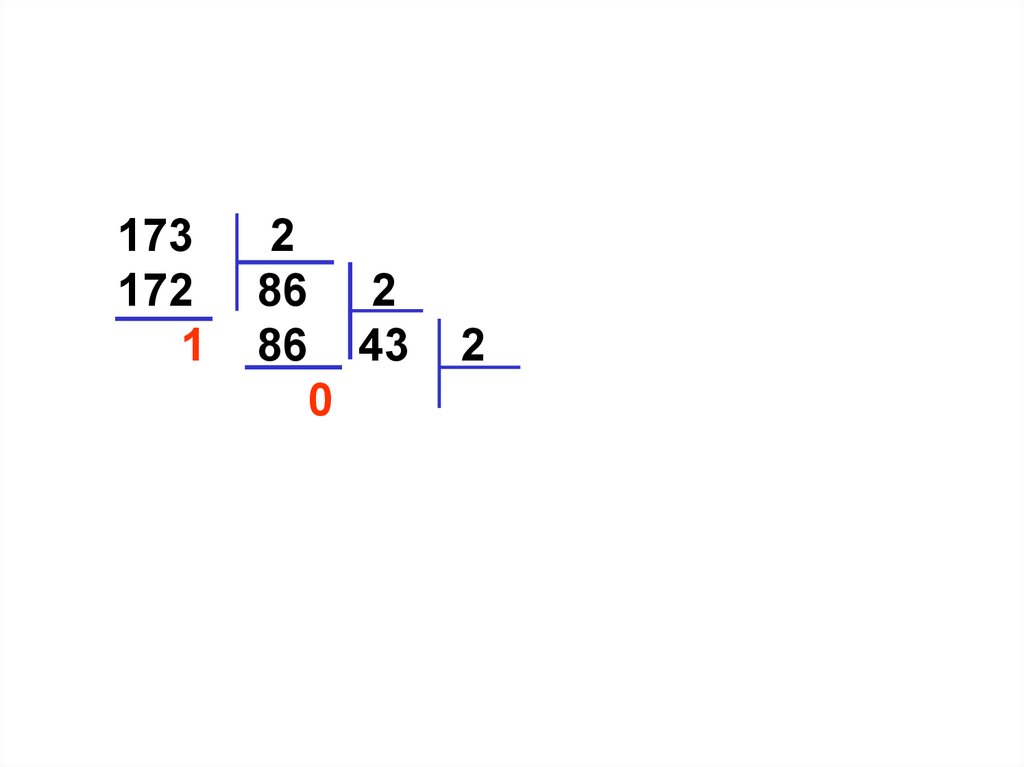
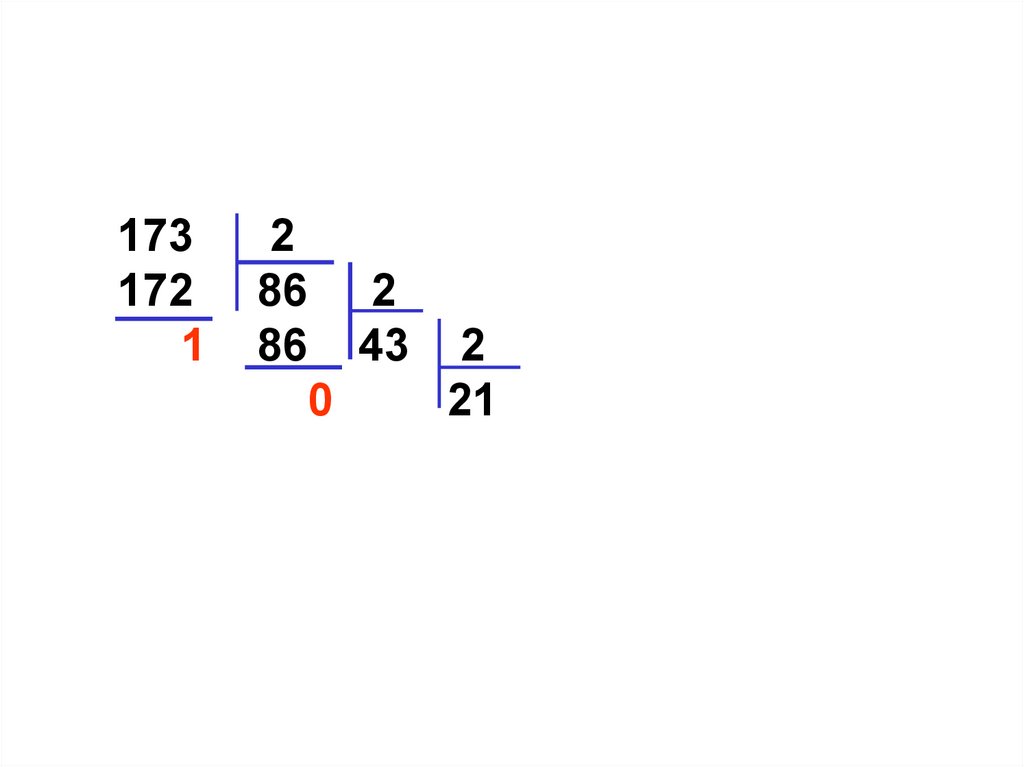
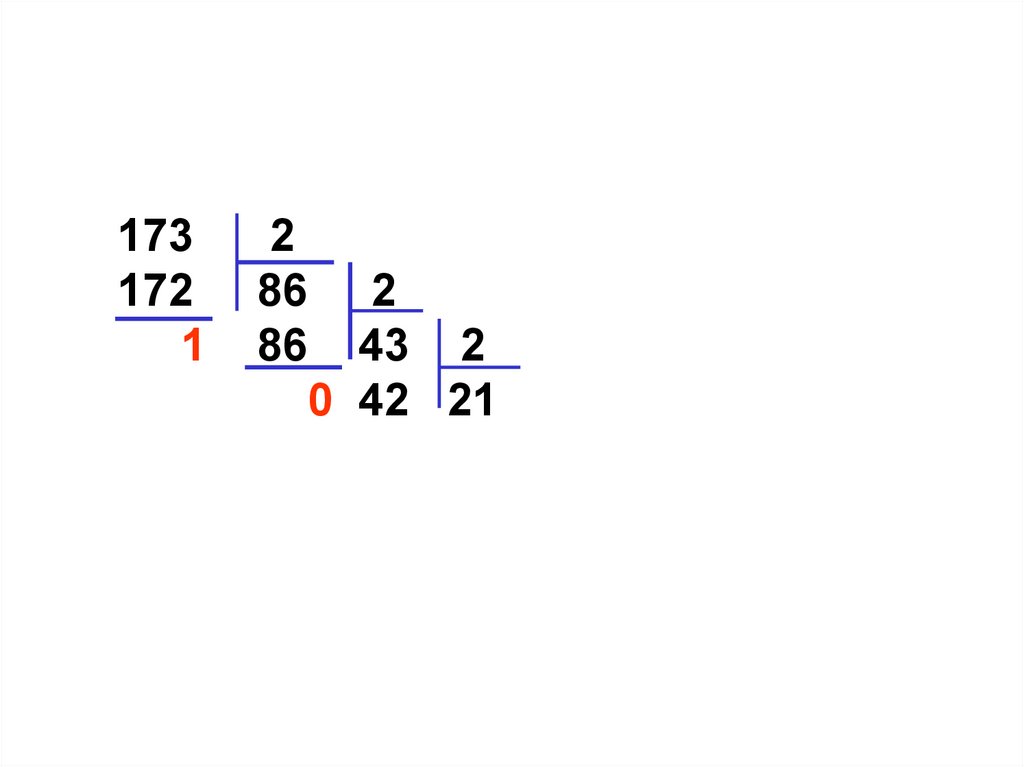
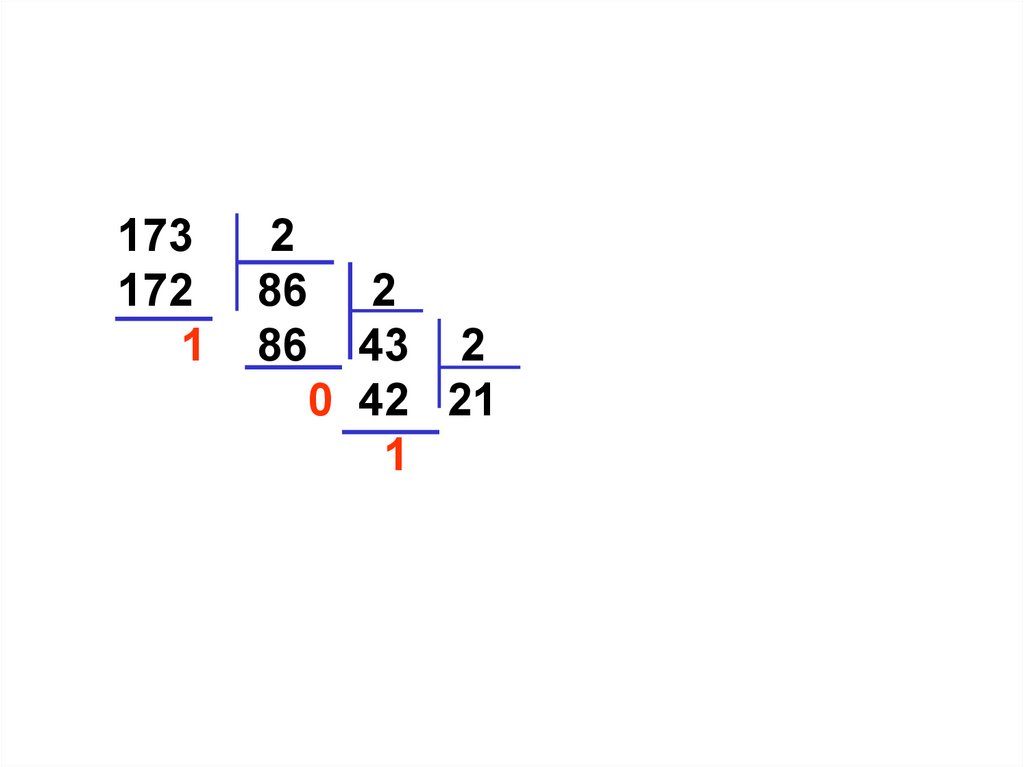
173172
1
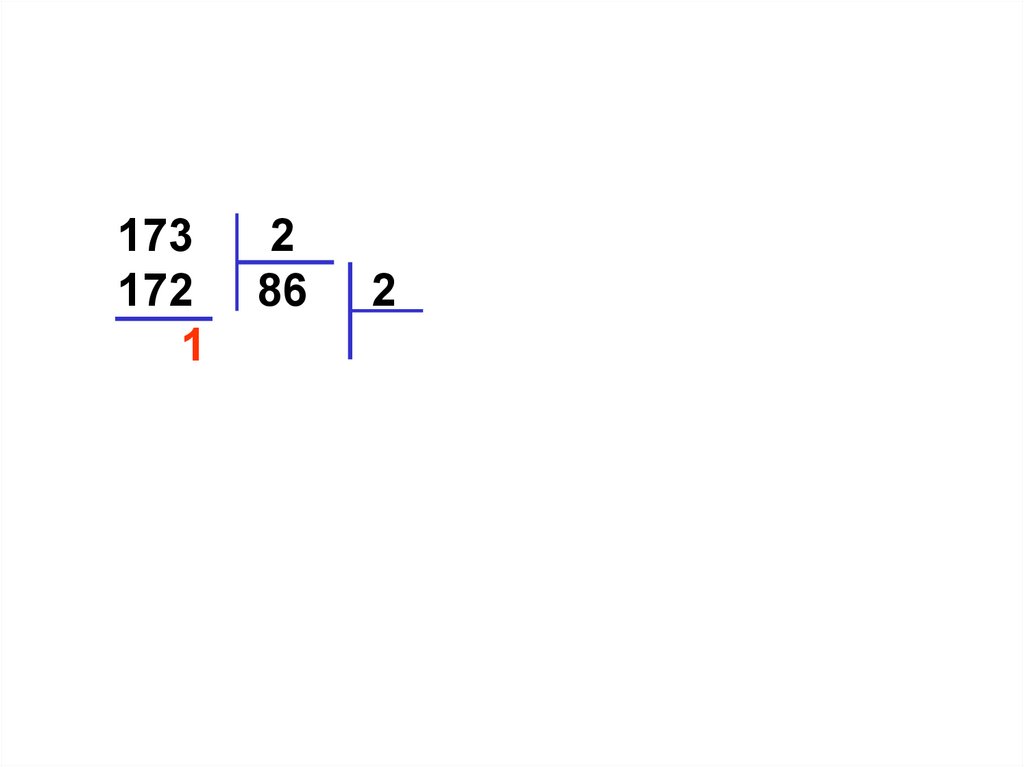
2
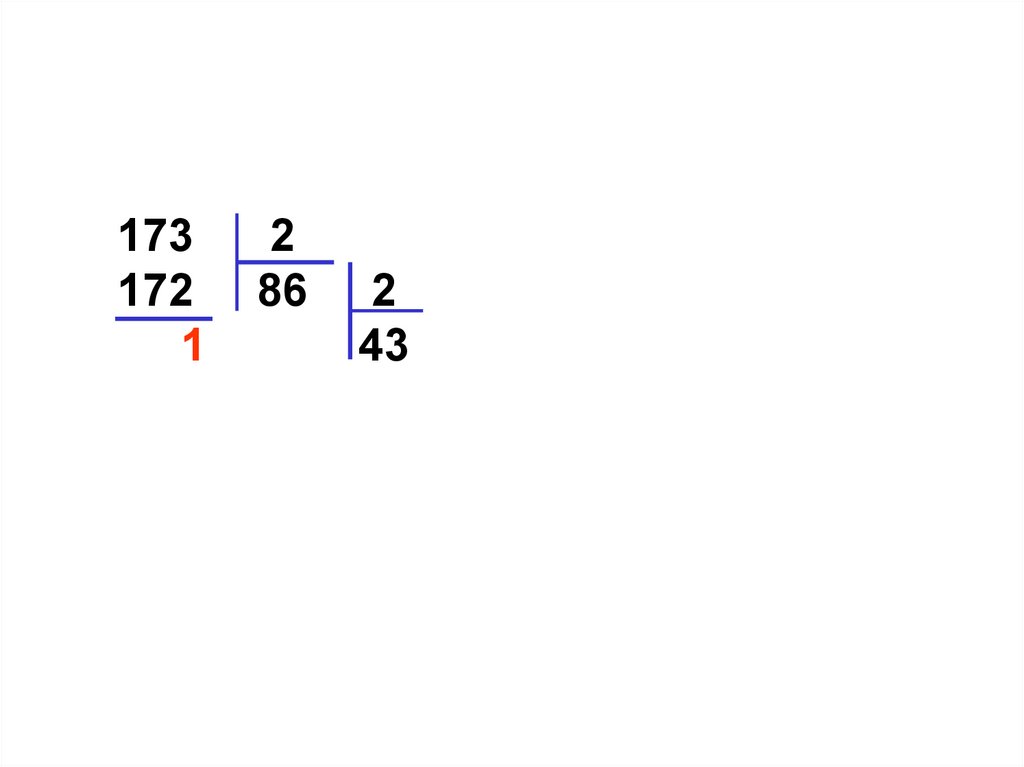
86 2
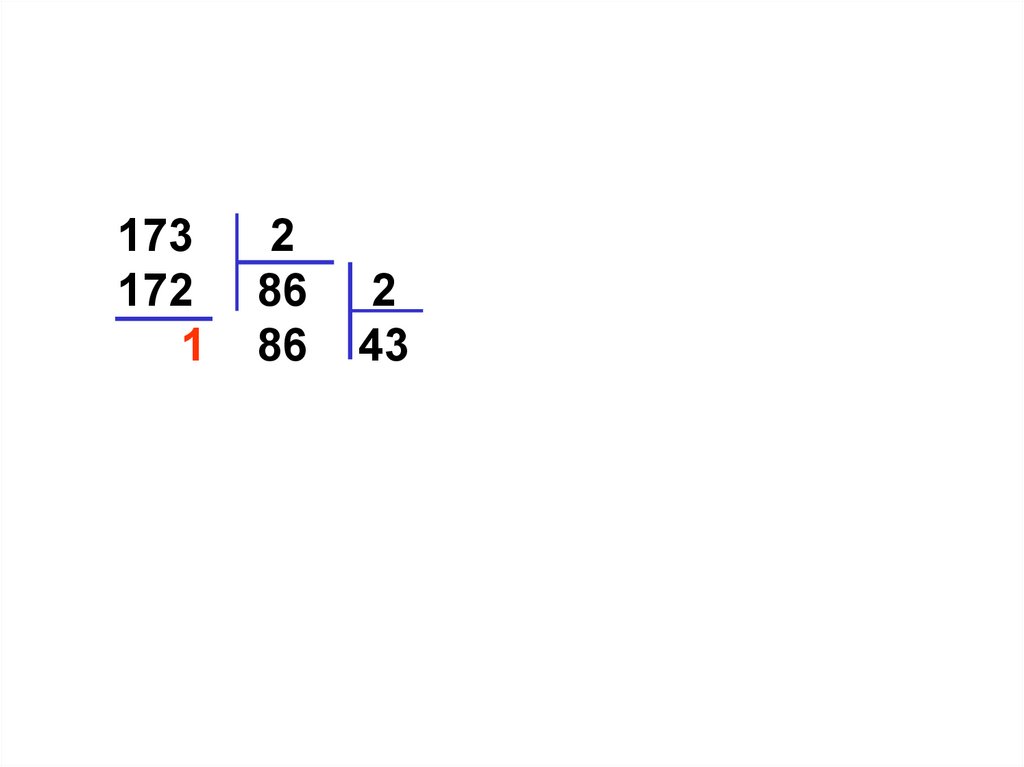
86 43 2
0 42 21 2
1 20 10
1 10
0
2
5 2
4 2 2
1 2 1
0
4.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10
1 10
0
2
5 2
4 2 2
1 2 1
0
5.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10
1 10
0
2
5 2
4 2 2
1 2 1
0
6.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10
1 10
0
2
5 2
4 2 2
1 2 1
0
7.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10
1 10
0
2
5 2
4 2 2
1 2 1
0
8.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10
1 10
0
2
5 2
4 2 2
1 2 1
0
9.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10
1 10
0
2
5 2
4 2 2
1 2 1
0
10.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10
1 10
0
2
5 2
4 2 2
1 2 1
0
11.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10
1 10
0
2
5 2
4 2 2
1 2 1
0
12.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10
1 10
0
2
5 2
4 2 2
1 2 1
0
13.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10
1 10
0
2
5 2
4 2 2
1 2 1
0
14.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10
1 10
0
2
5 2
4 2 2
1 2 1
0
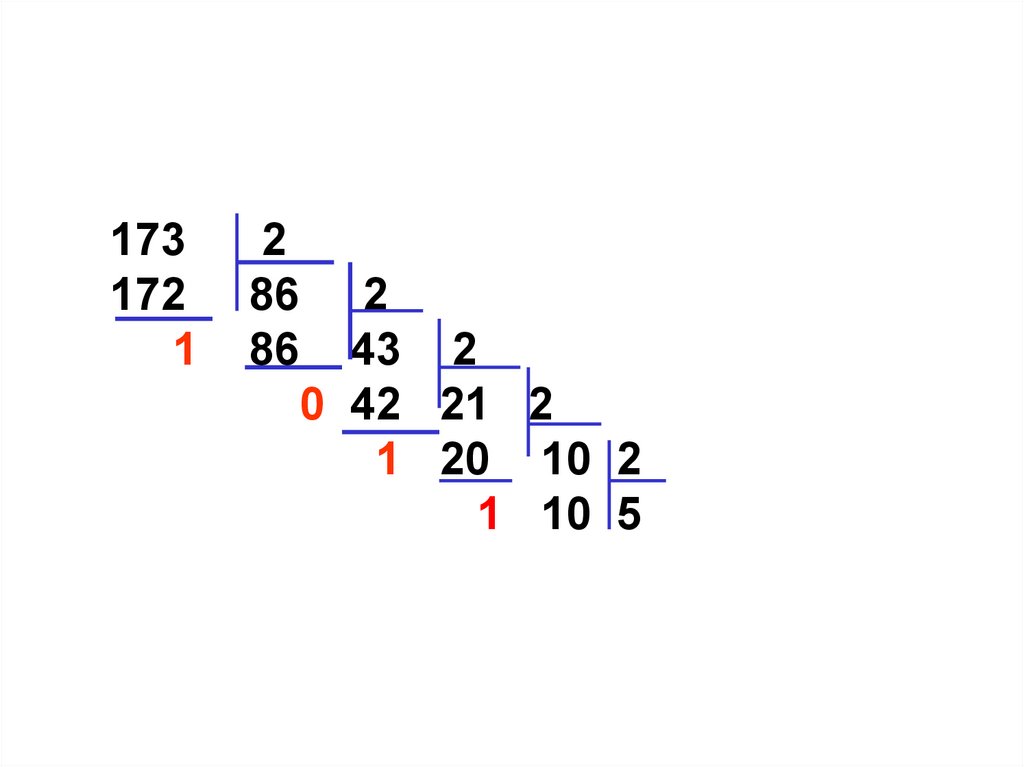
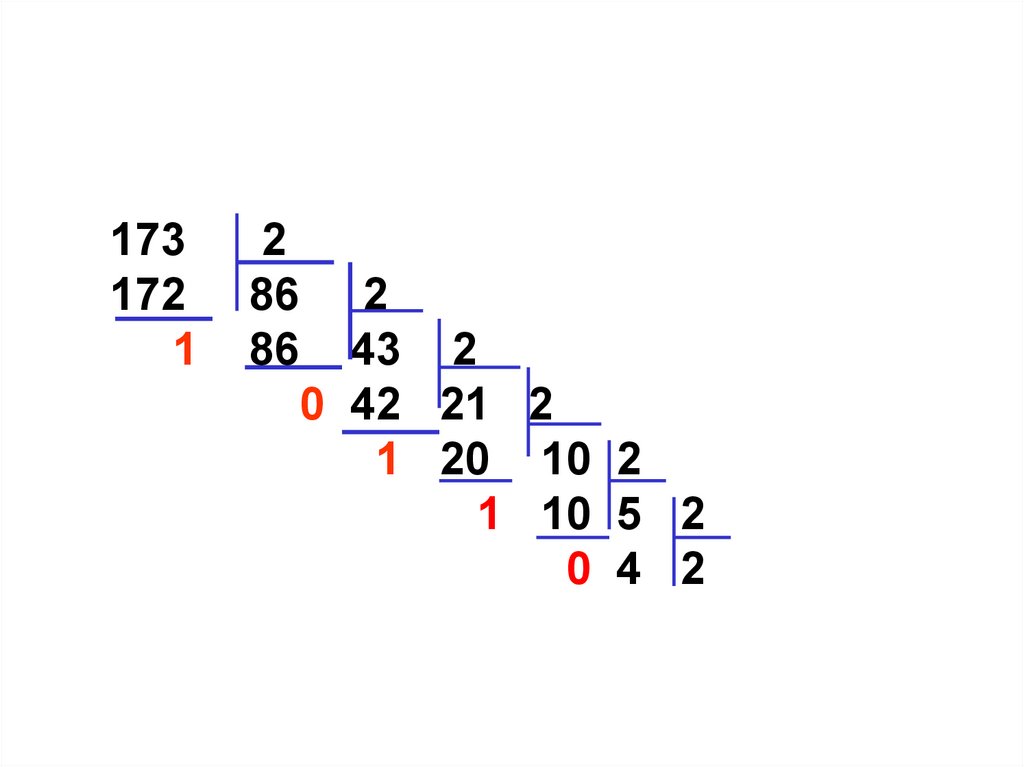
15.
173172
1
2
86 2
86 43 2
0 42 21 2
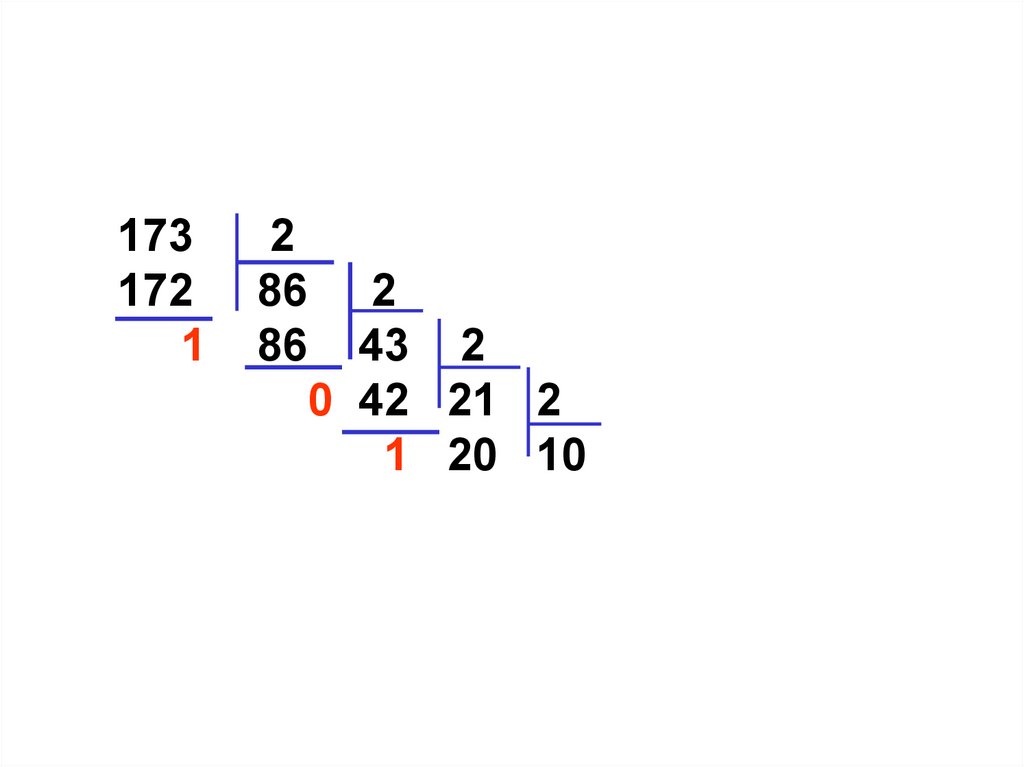
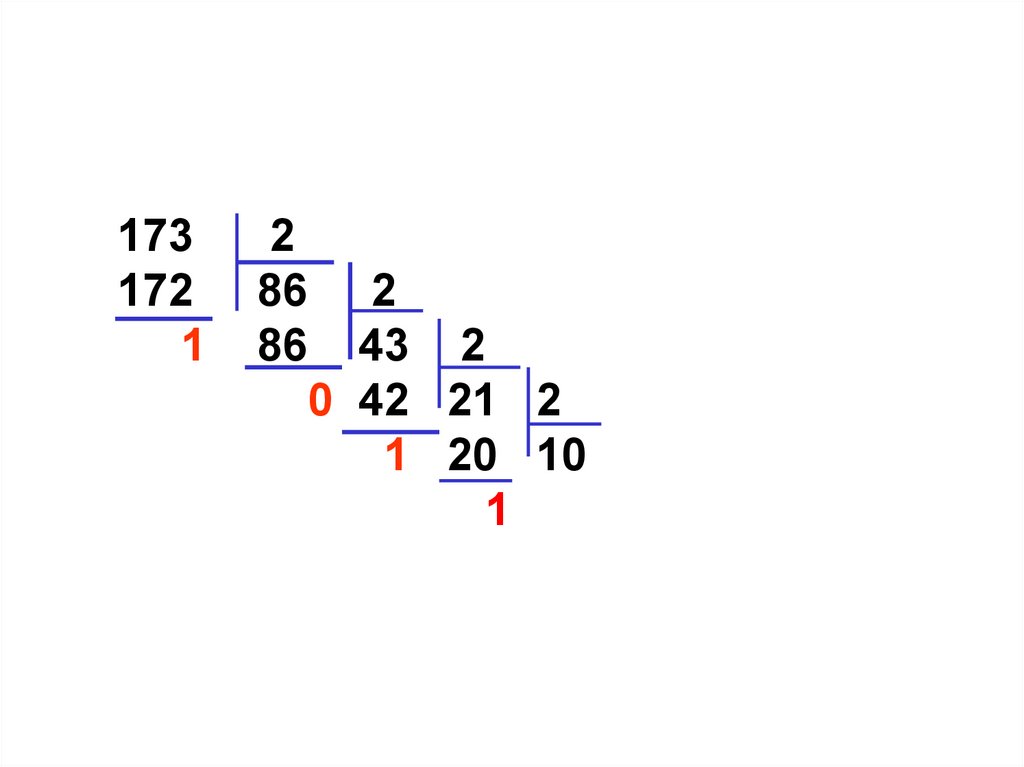
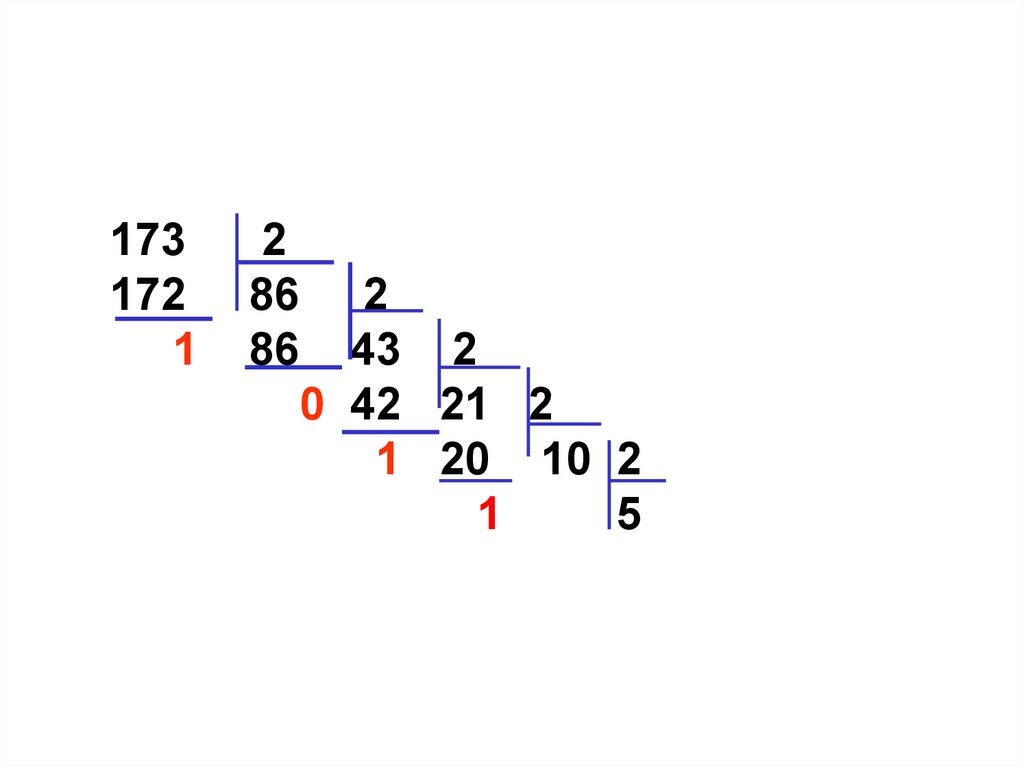
1 20 10 2
1 10 5 2
0 4 2 2
1 2 1
0
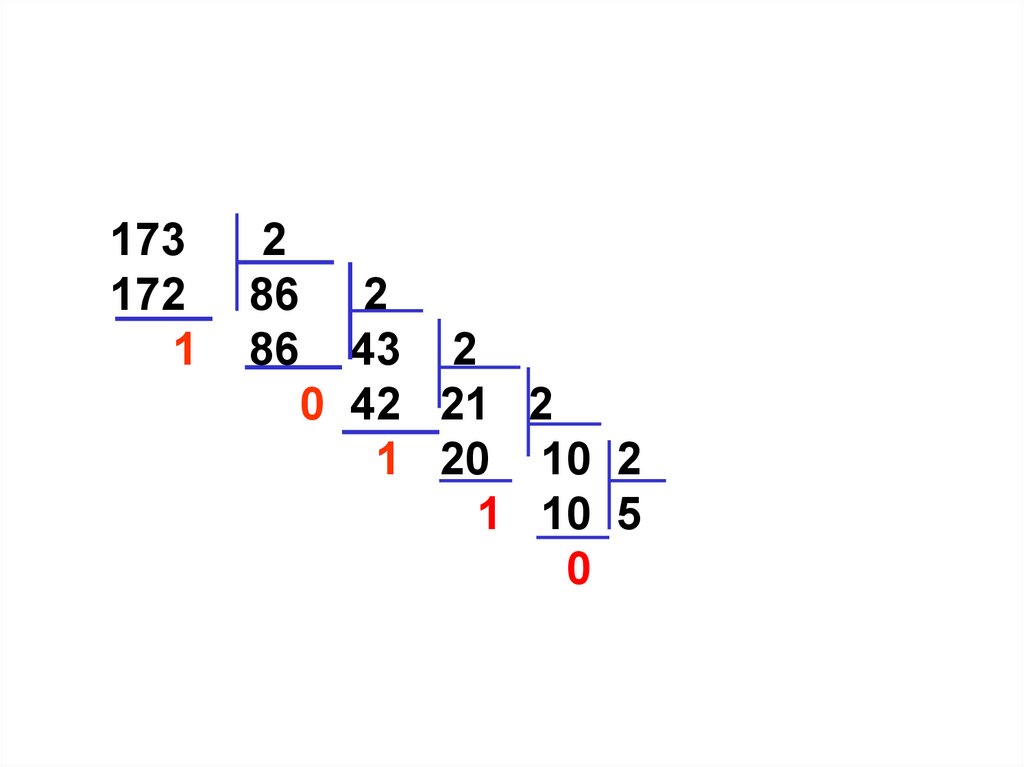
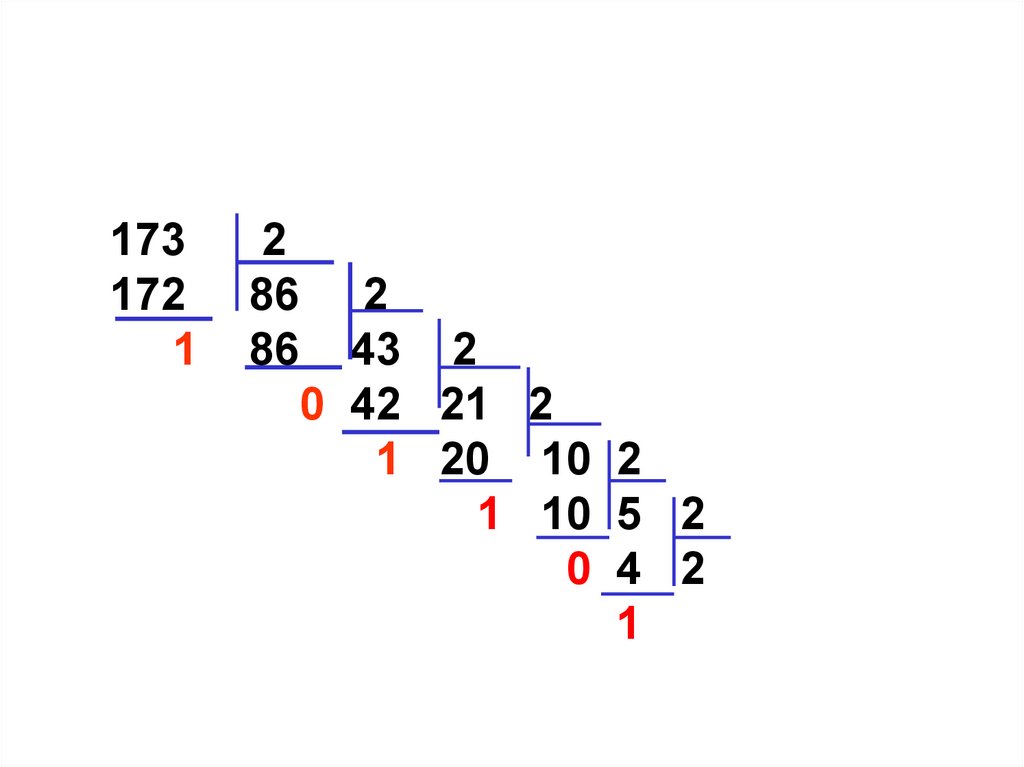
16.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10 2
1 10 5 2
0 4 2 2
1 2 1
0
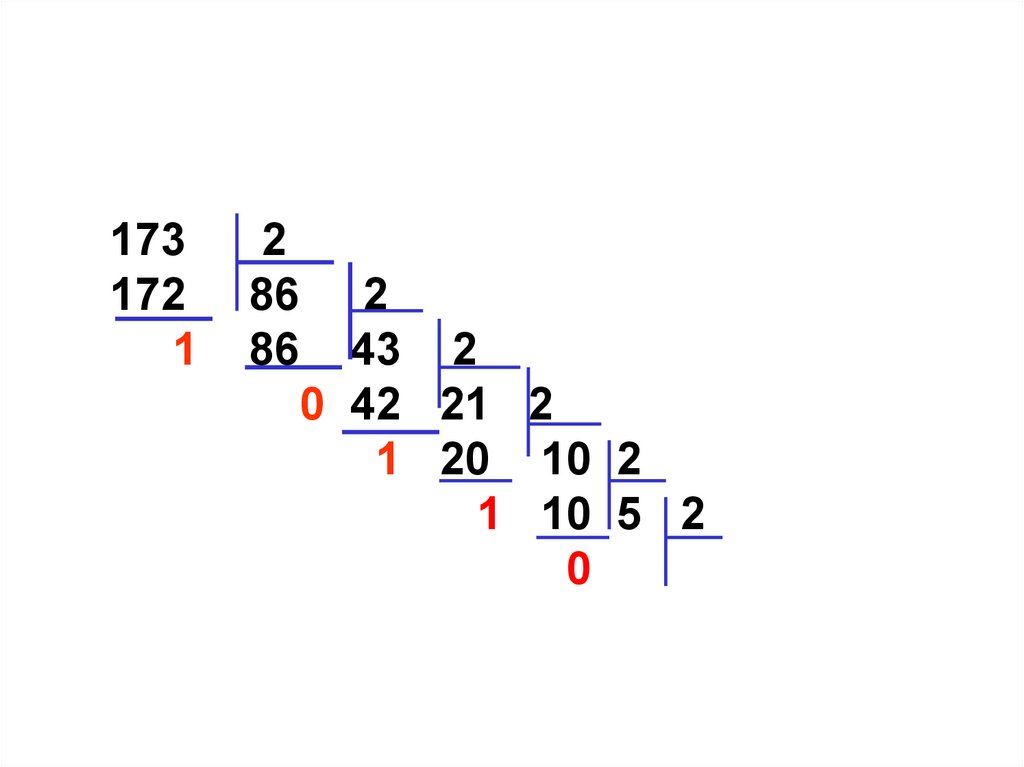
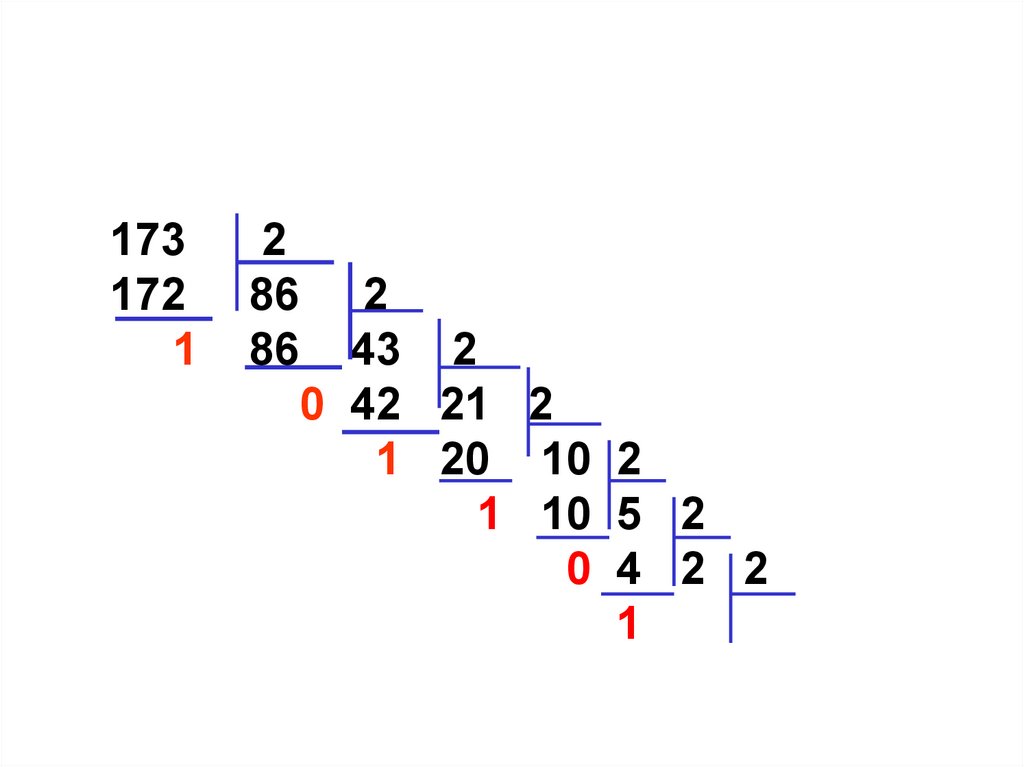
17.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10 2
1 10 5 2
0 4 2 2
1 2 1
0
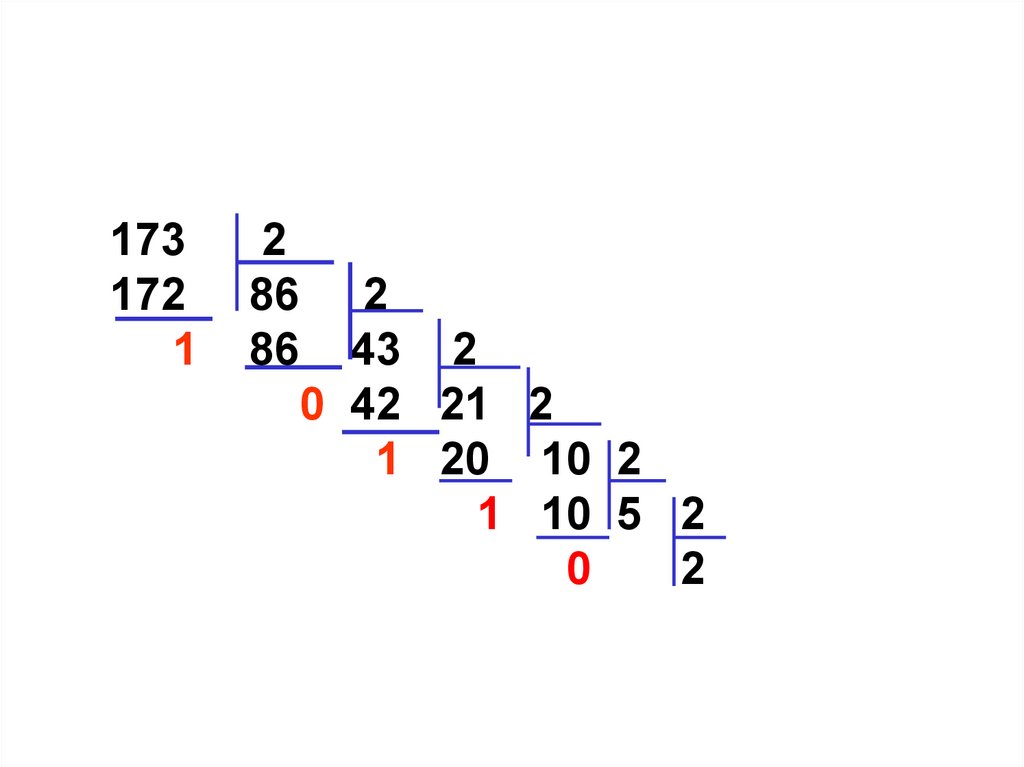
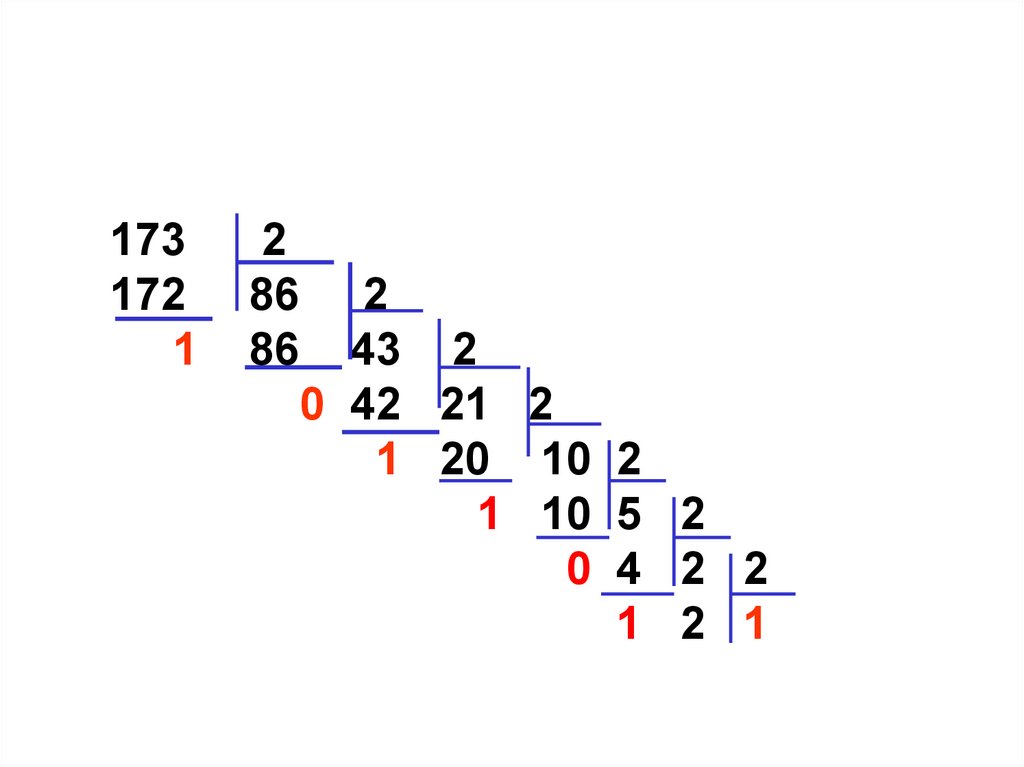
18.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10 2
1 10 5 2
0 4 2 2
1 2 1
0
19.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10 2
1 10 5 2
0 4 2 2
1 2 1
0
20.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10 2
1 10 5 2
0 4 2 2
1 2 1
0
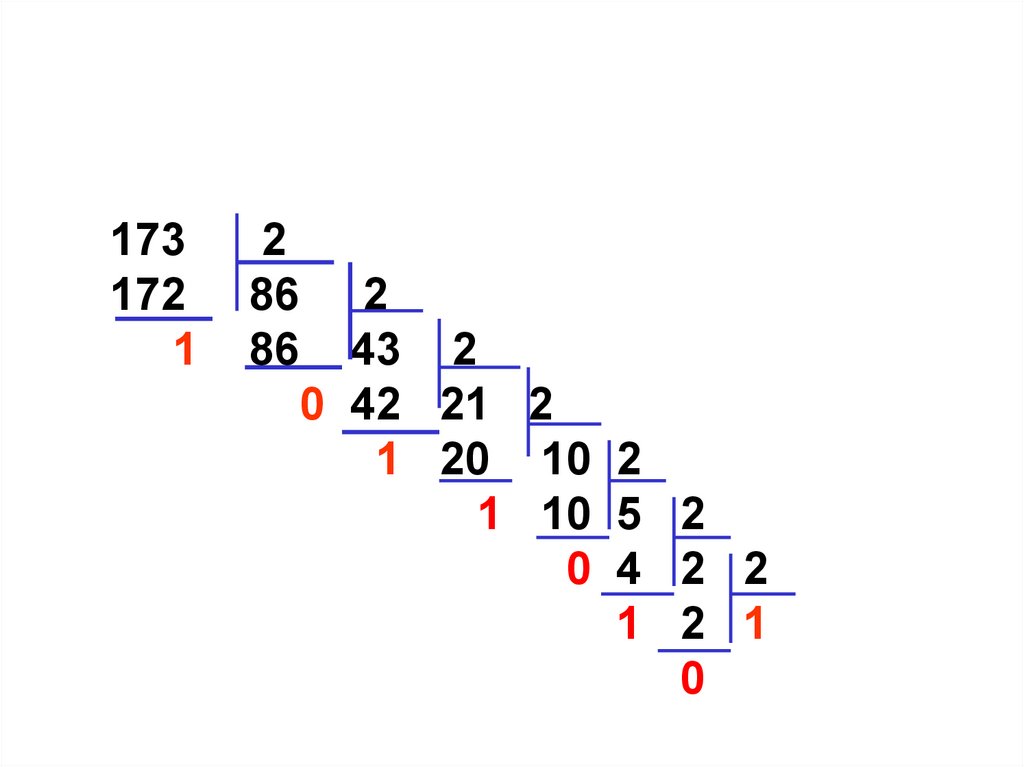
21.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10 2
1 10 5 2
0 4 2 2
1 2 1
0
22.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10 2
1 10 5 2
0 4 2 2
1 2 1
0
23.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10 2
1 10 5 2
0 4 2 2
1 2 1
0
24.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10 2
1 10 5 2
0 42 2
1 2 1
0
25.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10 2
1 10 5 2
0 4 2 2
1 2 1
0
26.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10 2
1 10 5 2
0 4 2 2
1 2 1
0
27.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10 2
1 10 5 2
0 4 2 2
1 2 1
0
28.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10 2
1 10 5 2
0 4 2 2
1 2 1
0
29.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10 2
1 10 5 2
0 4 2 2
1 2 1
0
30.
173172
1
2
86 2
86 43 2
0 42 21 2
1 20 10 2
1 10 5 2
0 4 2 2
1 2 1
0
31.
10
1
1
0
1
1
0
32. 17310 = 101011012
33.
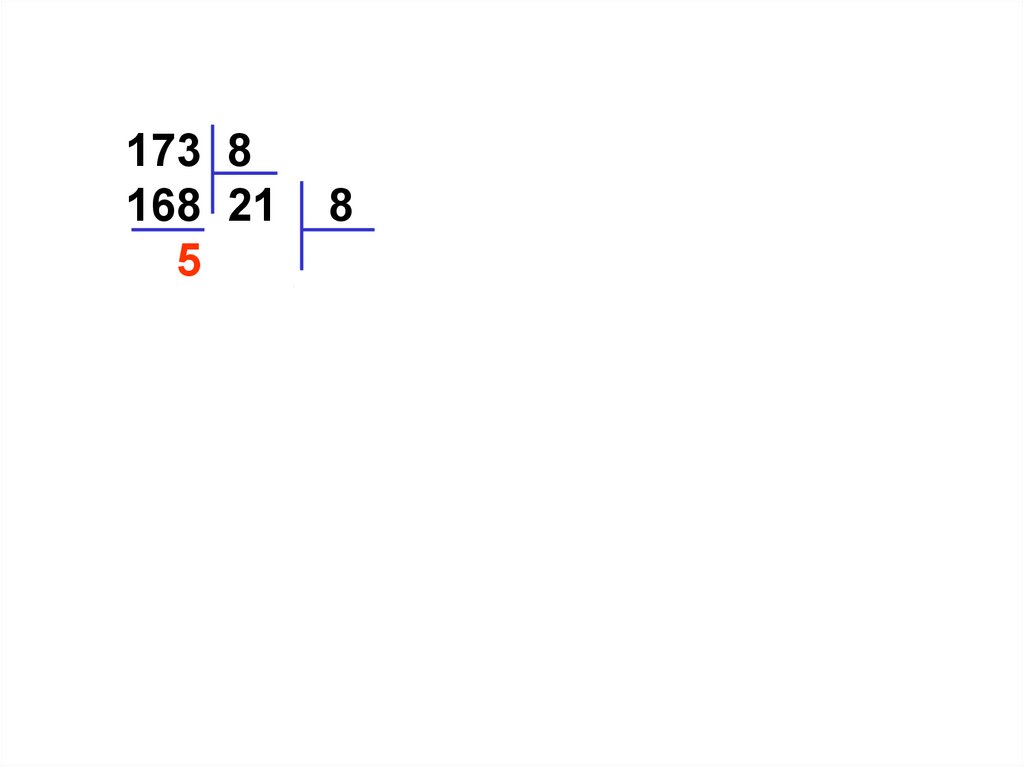
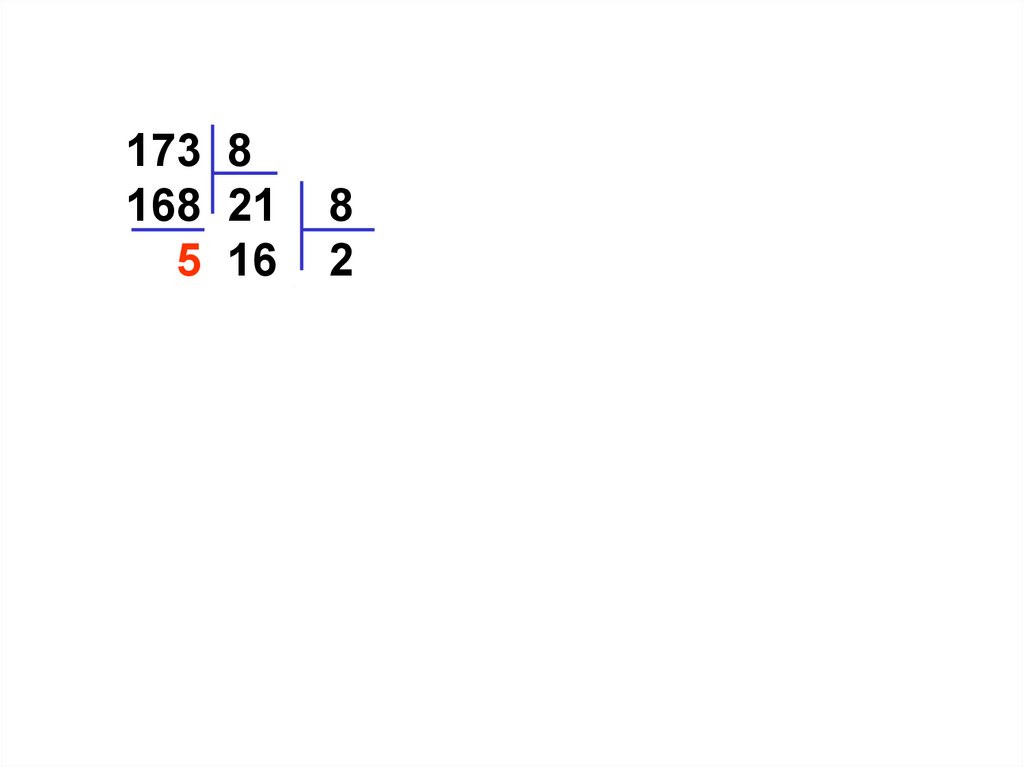
173 8168 21
5 16
5
8
2
34.
173 8168 21
5 16
5
8
2
35.
173 8168 21
5 16
5
8
2
36.
173 8168 21
5 16
5
8
2
37.
173 8168 21
5 16
5
8
2
38.
173 8168 21
5 16
5
8
2
39.
173 8168 21
5 16
5
8
2
40.
173 8168 21
5 16
5
8
2
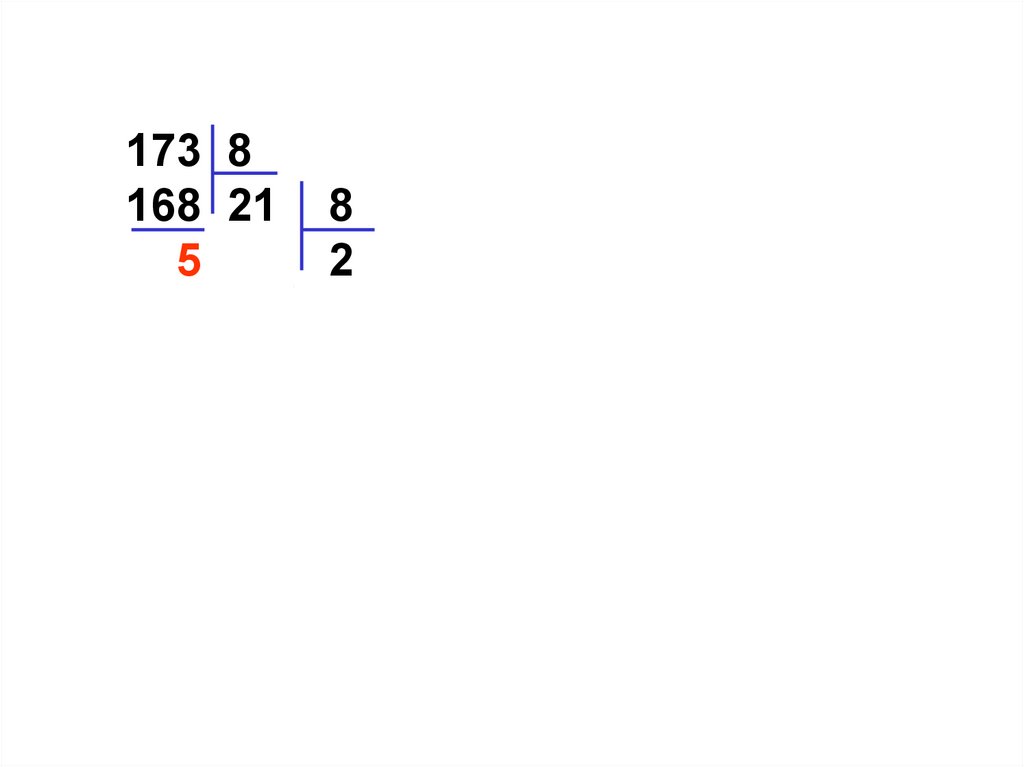
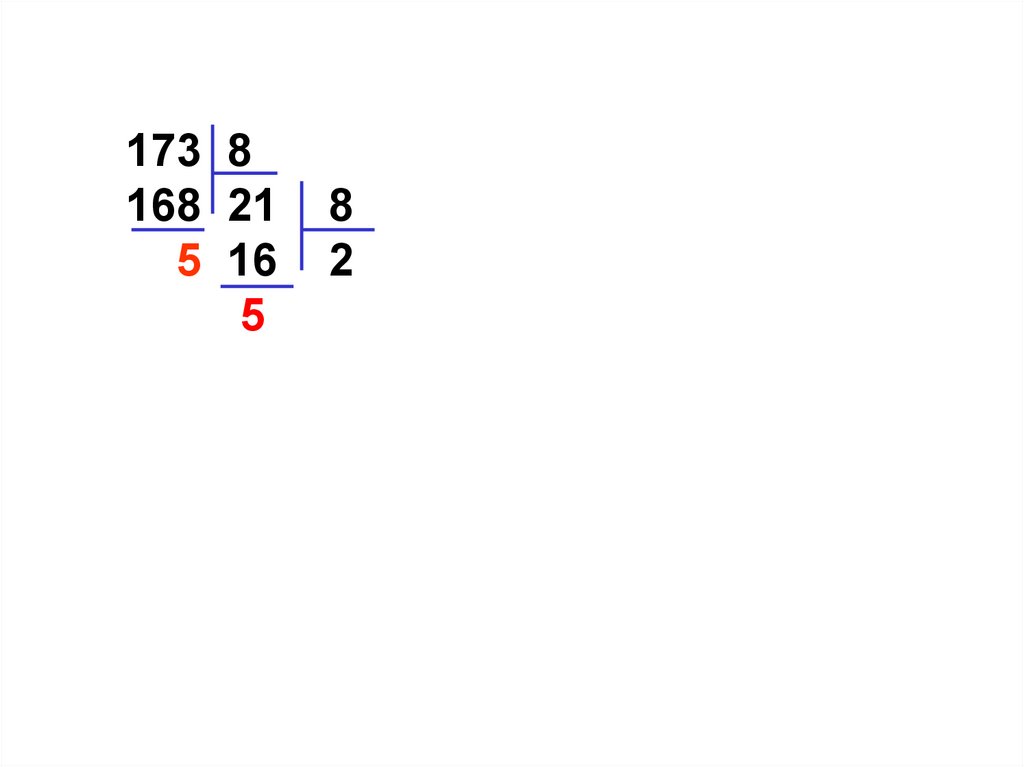
41. 17310 =
173 8168 21 8
5 16 2
5
17310 =
8
42.
173 16160 10
13
43.
173 16160 10
13
44.
173 16160 10
13
45.
173 16160 10
13
46. 17310 = АD16
173 16160 10 (А)
13(D)
17310 = АD16
47. Алгоритм
Последовательно выполнять делениеданного числа и получаемых неполных
частных на основание новой системы
счисления до тех пор, пока не получим
частное, меньшее делителя.
Полученные остатки, являющиеся
цифрами числа в новой системе счисления,
привести в соответствие с алфавитом новой
системы счисления.
Составить число в новой системе
счисления, записывая его, начиная с
последнего остатка (справа налево).










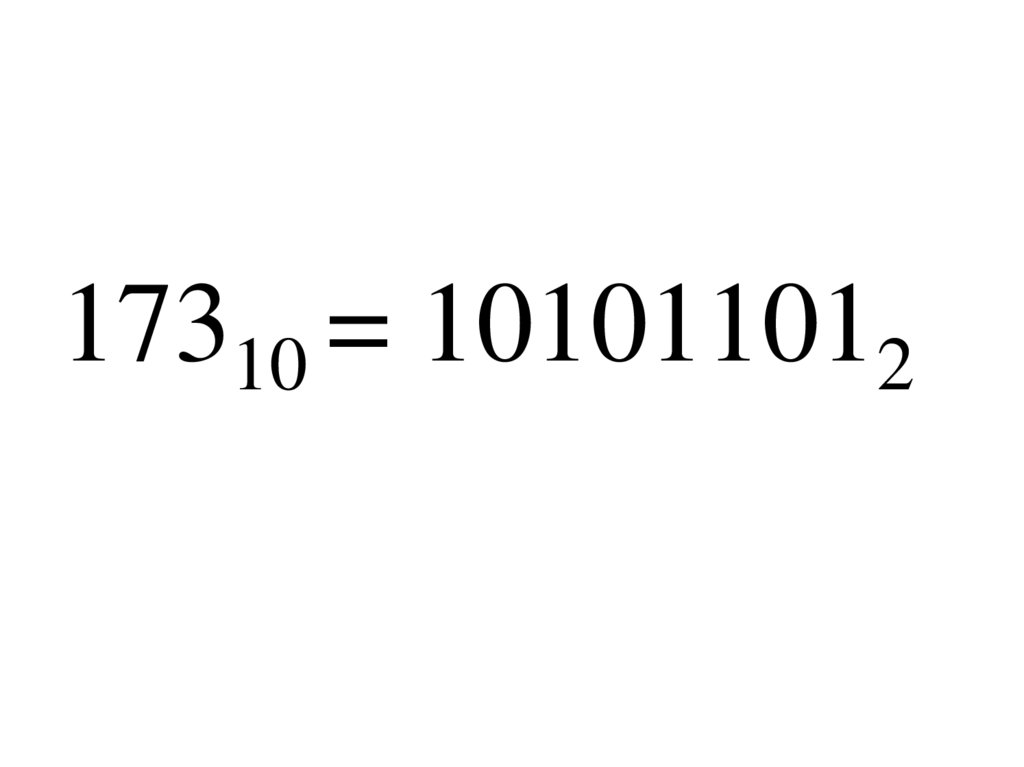











 Информатика
Информатика








