Похожие презентации:
Лекция 6. Численное интегрирование функций
Тема.
Численное интегрирование функций Решаемые задачи:
• вычисление объемов тел;
• вычисление площадей фигур;
• вычисление длин кривых;
• и т.д.
Численное интегрирование функций Подходы:
• замена исходной функцииf(x) (заданной таблично или аналитически) интерполирующим полиномомP(x) с известной первообразной;
• подбор оптимальных узлов интегрирования при аналитически заданной функцииf(x);
• вероятностные или статистические методы.
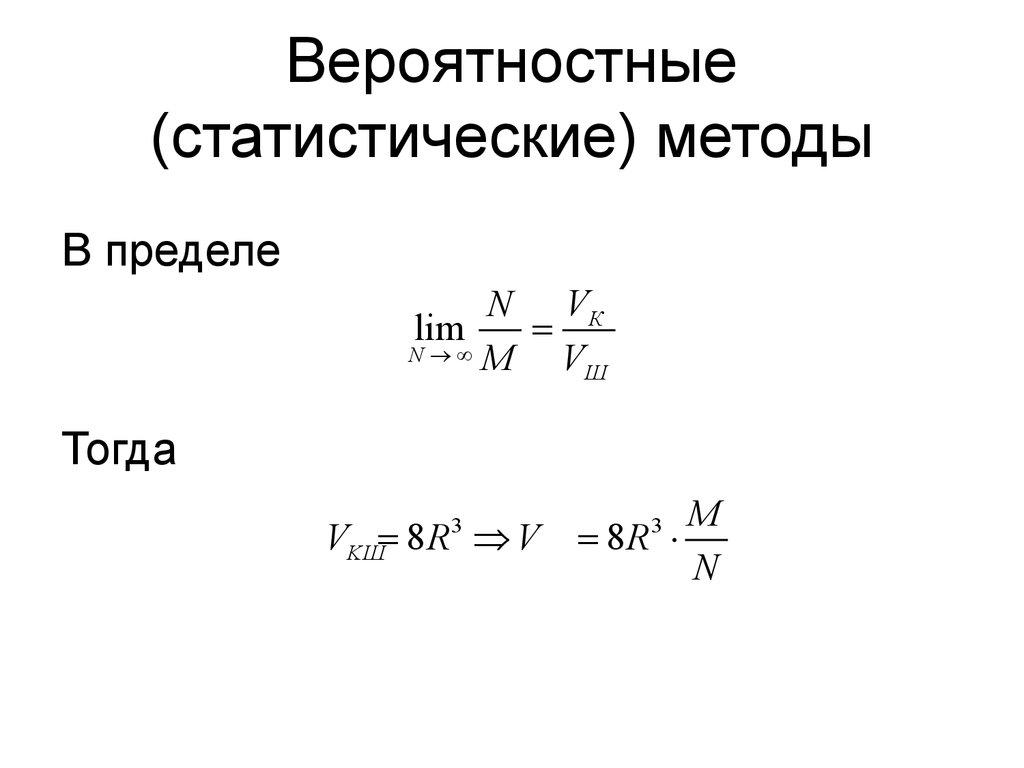
Вероятностные (статистические) методы Пример: задан шар Соотношение объёмов шара и куба, в который вписан шар: 2222iii xyzR ++≤КШVNVM≈ Вероятностные (статистические) методы В пределе ТогдаlimКNШVNMV →∞=3388KШM VRVRN =⇒=× Методы с подбором узлов На отрезке [–1,1] При переходе к отрезку[a,b] имеем ()()1niii Iftdtcft=−′==∑∫()1,2bniiiaba Ifxdxcfx=−==∑∫.22ii babaxt +−=+ Интегрирование интерполирующих полиномов При заменеf(x) интерполирующим полиномом() ()()() ()()()()1110010,,1 ,,,0,1,..., ipipipnipxxp iiiijijjxxxbxmmiiaxxp iijijipipi IfxdxPxdxPxcxn IIfxdxPxdxmp fxPxcxxxximϕ+++====+= =≈= ==≈=− ≈=∈= ∑ ∫∫ ∑∑ ∫∫∑ Интегрирование интерполирующих полиномов При заменеf(x) интерполирующим полиномом()10,1ipxppmmx ijijijijx ijijxmi IcxdxcxdxnImpϕ+ ===== ==Φ= ==− ∑∑∑∑∫∑ Интегрирование интерполирующих полиномов Формулы прямоугольников:
• левосторонних;
• правосторонних;
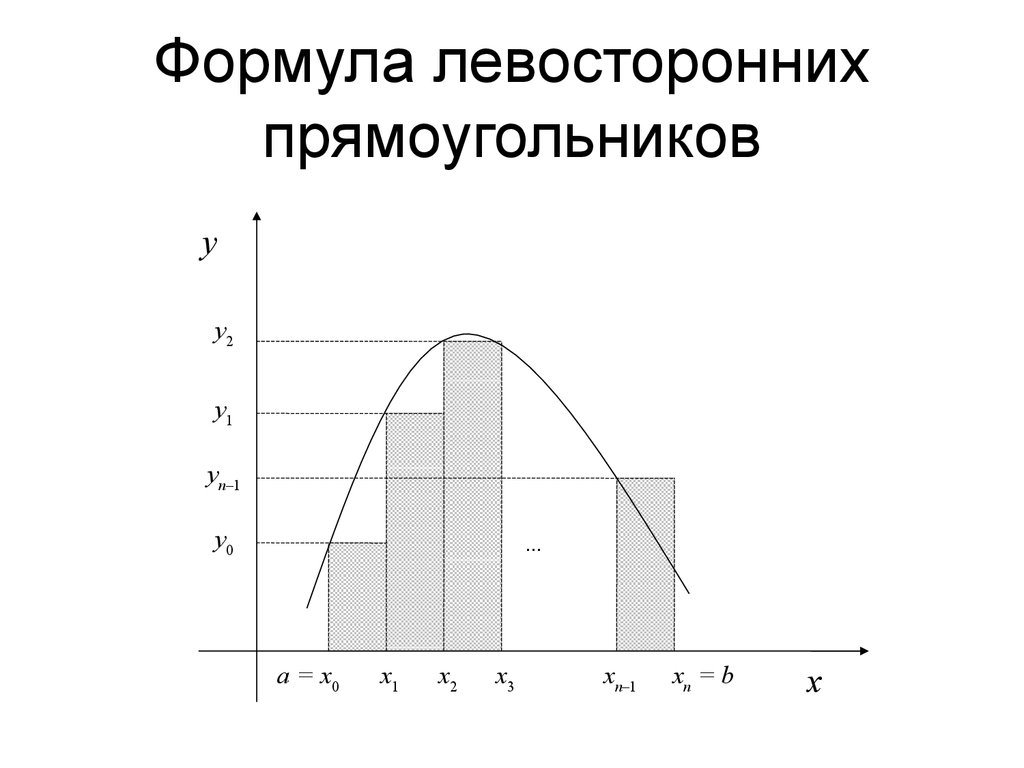
• центральных.xixi12iixx+yiyi12iixxf+ ÷ Формула левосторонних прямоугольников На отрезке[xi,xi+1] полагаемp =1,Pi(x) =yi.
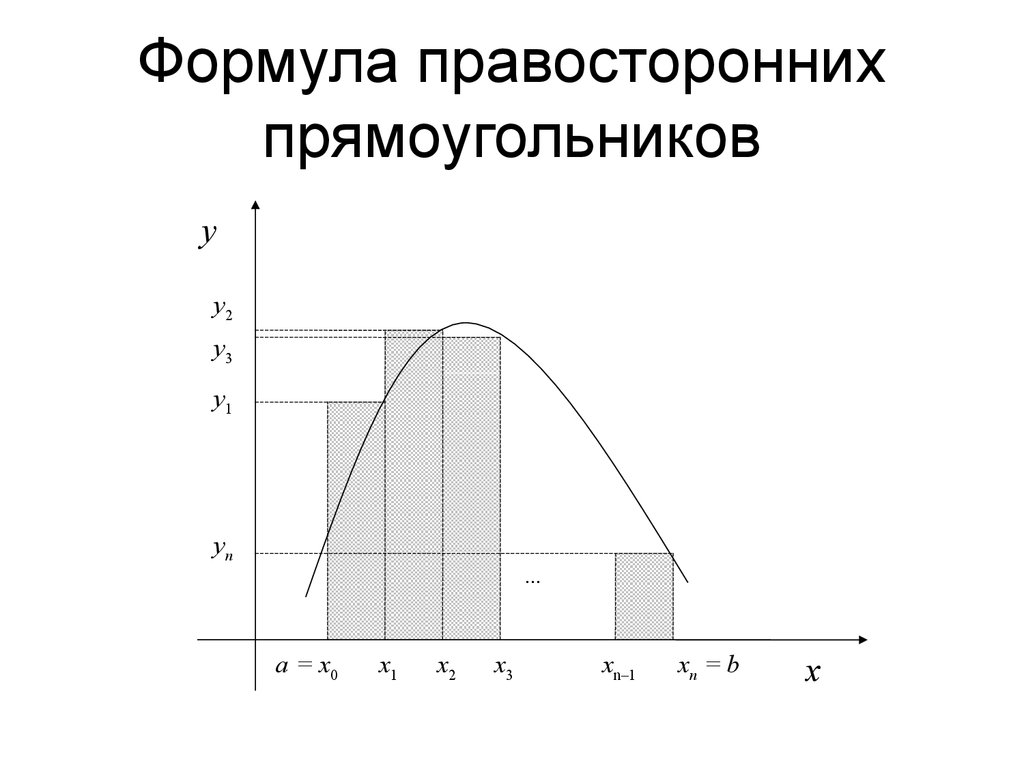
Получаем: Для равномерной сетки()1011001,nixnnxiiixiix iiii Ifxdxyxyh hxxx+ −−==+ =≈= =∆=− ∑∑∫()010nxnix Ifxdxhy−= =≈∑∫ Формула левосторонних прямоугольниковyx… a = x0x1x2x3xn –1xn = by0y1y2yn –1 Формула правосторонних прямоугольников На отрезке[xi,xi+1] полагаемp =1,Pi(x) =yi+1.
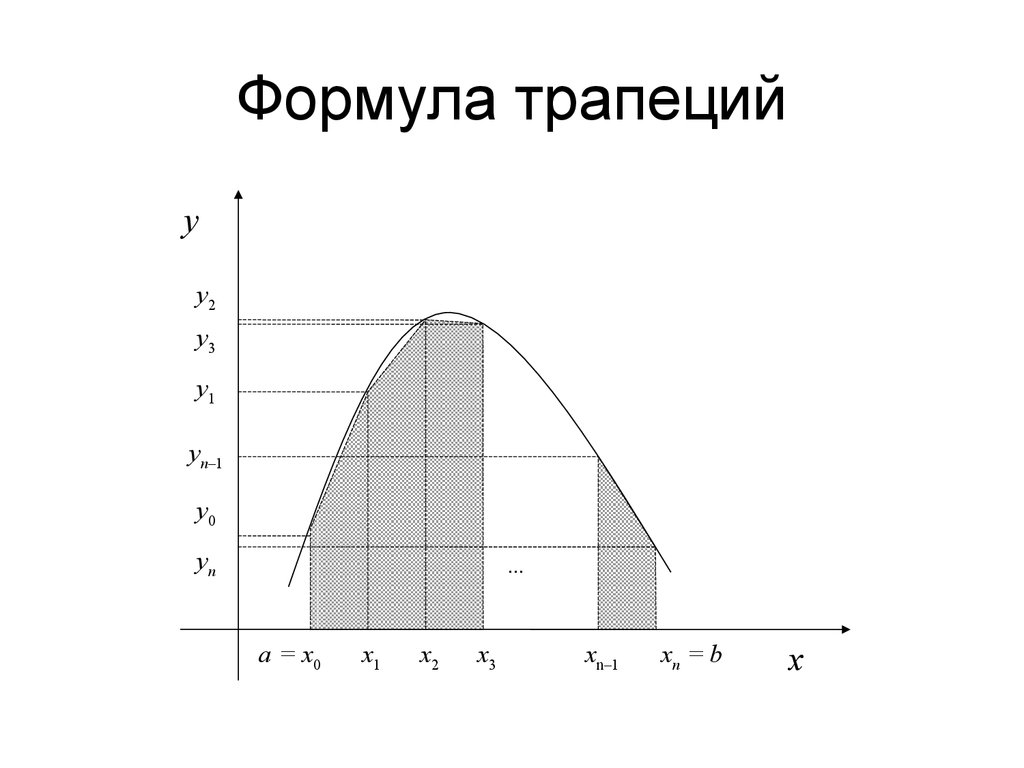
Получаем: Для равномерной сетки()1011001,nixnnxiiixiix iiii Ifxdxyxyh hxxx+ −−++==+ =≈= =∆=− ∑∑∫()001nxnniix Ifxdxhyhy−+== =≈= ∑∑∫ Формула правосторонних прямоугольниковyx… a = x0x1x2x3x n–1y3y1y2ynxn = b Формула центральных прямоугольников На отрезке[xi,xi+1] полагаемp =1, Получаем:()10110022nixnnx iiiiixiix xxxx Ifxdxfxfh+ −−++==++ =≈= ÷÷ ∑∑∫()0102nxniiixxx Ifxdxhf−+=+ =≈ ÷ ∑∫()12iiixxPxf+ = ÷ Формула трапеций На отрезке[xi,xi+1] полагаемp =1,()1iiiiiiyy Pxxxyh+− =−+()121212122iiiiiiixii iiiiiiixyy PxdxxxyxChyy IxxyxCyyhh+− =−++⇒ − ⇒=−++=+ ÷ ∫ Формула трапеций На отрезке[a,b] Для равномерной сетки()111 100110011122nnn iiiiiiinniii IIhyyyhyhhyh −−− +−−=== ==+=+++ ÷ ∑∑∑()111001222nn iiiniihh Iyyyyy −−+== =+=++ ÷ ∑∑ Формула трапецийyx… a = x0x1x2x3x n–1y3y1y2ynxn = byn –1y0 Квадратурные формулы Вспомним формулу Выполним подстановку:() ()()110, ipipxxp iiiijijjxx IfxdxPxdxPxcxϕ++= =≈=∑ ∫∫()1(1)00ip ipipxpp iijijijijjjxx Icxdxcxdx ϕϕ+== ÷ ≈= ÷ ∑∑ ∫∫ Квадратурные формулы Если предположить, чтоcij =yip+j⋅Cij , то гдеAij – квадратурные коэффициенты.
Тогда ()() (1)(1)0, ipipxxpp iijijipjijijjjxxp ijipjj IcxdxyCxdxAy ϕϕ+++==+= ÷÷ ≈=×= ÷÷ = ∑∑ ∫∫∑000,1.pmm iijipjiijn IIAymp+=== ===− ∑∑∑ Квадратурные формулы ЕслиPi(x) =Lp,i(x) , т.е.
то ()(),0,pipk ppiipjjk ipjipkkjxx PxLxyxx+=++≠ − ÷== ÷− ÷ ∑∏()001,.pp ijijipkkk ipjipk kjkj Cxxxxxϕ+==++ ≠≠ ==−− ∏∏ Квадратурные формулы Тогда Дляp= 1 имеем:() (1)(1)001 ipipxxpp ijijijipkjj ipjipkxx jkjk ACxdxxxdxxxϕ+++==++ ≠≠ ==−− ∏∏ ∫∫ ()()1 11,111iiiii iiii xxxx PxLxyy xxxx+++ −−==+ −− ()() 0101111,,, iiiiii iiii CCxxxxxx xxxx ϕϕ+++ ===−=− −− Квадратурные формулы Интегрируем:()12121221112110;22110222ixiiiiiixiiiiiiiixiiiiiixxx Axxdxxxhxxh Axxdxhxx xxxxhhh+− =−=−=− − =−−==−= ÷− −− ==−= ÷ ∫ Квадратурные формулы В итоге Получили формулу трапеций.()11,222iii iiiiihhh Iyyyy++ =+=+()10012mn iiiiii IIhyy−+====+ ∑∑11,1nmn =−== Квадратурные формулы Дляp= 2 имеем: ()() 2122 22,2 221222 222221 2122 21221222222221ii iiiiii iiiiiiii xxxx PxLxy xxxx xxxxxxxxyy xxxxxxxx++ ++++++ −−==+ −− −−−−++ −−−− ()() ()()() ()() ()()() ()() ()()() 002122 221222 11222 2122122 21221 22222211,,1,,1,, iiii Cxxxxx xxxx Cxxxxx xxxx Cxxxxx xxxxϕ++++++++++ ==−− −− ==−− −− ==−− −− Квадратурные формулы Интегрируем: и т.д.
()()()222222 02122 2212222 21222122 22122122212126ixiii iiiix iiiiiiixiii Axxxxdx xxxx xxxxxxdxhhhhhh+++ +++++ =−−= −− =−++= −−−+ =−∫ Квадратурные формулы В итоге получим: Это формула Симпсона: ()()() ()()3 21222121201 2212 2122122212,,6626 iiiiiiiiiii iiiii hhhhhhAAhhh hhhhAh+++++++ +−+== +−= ()()(())2212 21221221221212 221222262ii iiiiiiiiii iiiihh Ihhhyhhyhh hhhy+ ++++++++ =−+++ +− Квадратурные формулы Для отрезка[a,b] ()()(())2212 212212212210212 221222262,12mii iiiiiiiiii iiiihh Ihhhyhhyhhn hhhym+ ++++=++++ =−+++ +−=−∑ Квадратурные формулы Если сетка равномерная, то т.е.
коэффициентыAj не зависят от индексаi .
Для отрезка[a,b]000,1.pmm ijipjiijn IIhAymp+=== ===− ∑∑∑()110.
ipipipxp iipjipjjxip IPqdxhPqdqhAy+++====∑ ∫∫ Квадратурные формулы Интерполирующий полином т.е.
()()()()01!!ppjjppjkkjy PqLqqkjpj−=≠ ÷ ==−− ÷− ÷ ∑∏() ()()01,!!pjpjjkkj Cqqkjpjϕ−=≠− ==−−∏ Квадратурные формулы Тогда()001!!ppjpjjjkkj ACqdqqkdqjpjϕ−=≠− ==−−∏ ∫∫ Коэффициенты Ньютона- Котеса В случае равномерной сетки положим ЗдесьHi – коэффициенты Ньютона- Котеса .
Т.е.1.jjHAp=()01!!pjpjkkj Hqkdq pjpj−=≠− =−−∏∫ Коэффициенты Ньютона- Котеса Свойства коэффициентов Ньютона- Котеса:01);
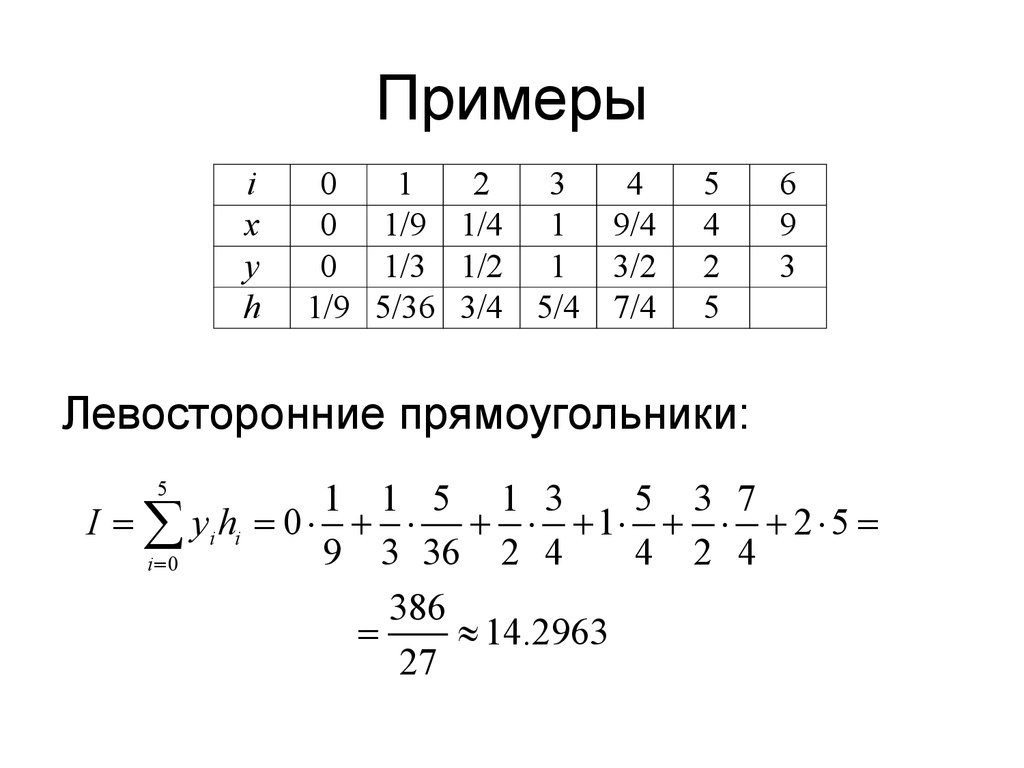
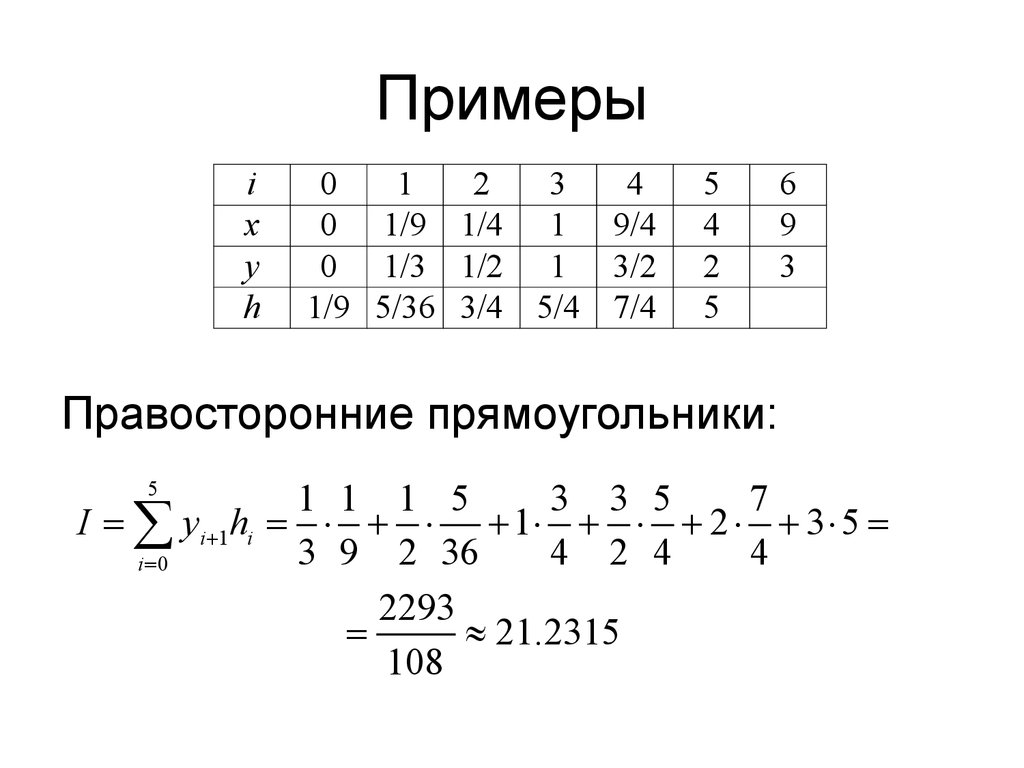
2)1.jpjpjHHH−=∑ Примерыn = 6i 0123456x 01/91/419/449y 01/31/213/223 012345 111151395 0;;1;1;
994936444497 4;94544 hhhhhh =−==−==−==−= =−==−= Примеры Левосторонние прямоугольники:i 0123456x 01/91/419/449y 01/31/213/223h 1/95/363/45/47/4550 11513537 0125 933624424386 14.296327iiiIyh= ==×+×+×+×+×+×= =≈∑ Примеры Правосторонние прямоугольники:i 0123456x 01/91/419/449y 01/31/213/223h 1/95/363/45/47/45510 11153357 1235 392364244 2293 21.2315108iiiIyh+= ==×+×+×+×+×+×= =≈∑ Примеры Трапеции:i 0123456x 01/91/419/449y 01/31/213/223h 1/95/363/45/47/45()510 11115113101 2293363242 53731297 1252317.7639 424372iiii Ihyy+= =+=×++×++×++ ÷÷÷ ×++×++×+=≈ ÷÷÷ ∑ Примеры Формула Симпсона:i 0123456x 01/91/419/449y 01/31/213/223h 1/95/363/45/47/45 ()()(())2212 212212212210212 22122226 53619515220 65361936936 51115112 369393692ii iiiiiiiiii iiiihh Ihhhyhhyhh hhhy+ ++++=++++ =−+++ + +−=××−×+ ÷ ×× ++×+××−×+÷ ÷÷÷ ∑ Примеры Формула Симпсона:2 543453515321 65434444244 353357473 2525 4442657442 77791211 5225518.0974 4445040+ +××−×++×+ ÷÷ ×× + +××−×+××−×+ ÷÷ ÷ ×× ++×+××−×=≈ ÷÷÷ Примеры Точность интегрирования:IδI ЛП 14.296320.6%I ПП 21.231517.9%IТ 17.76391.31%IС 18.09740.54%9018
Численное интегрирование функций Решаемые задачи:
• вычисление объемов тел;
• вычисление площадей фигур;
• вычисление длин кривых;
• и т.д.
Численное интегрирование функций Подходы:
• замена исходной функцииf(x) (заданной таблично или аналитически) интерполирующим полиномомP(x) с известной первообразной;
• подбор оптимальных узлов интегрирования при аналитически заданной функцииf(x);
• вероятностные или статистические методы.
Вероятностные (статистические) методы Пример: задан шар Соотношение объёмов шара и куба, в который вписан шар: 2222iii xyzR ++≤КШVNVM≈ Вероятностные (статистические) методы В пределе ТогдаlimКNШVNMV →∞=3388KШM VRVRN =⇒=× Методы с подбором узлов На отрезке [–1,1] При переходе к отрезку[a,b] имеем ()()1niii Iftdtcft=−′==∑∫()1,2bniiiaba Ifxdxcfx=−==∑∫.22ii babaxt +−=+ Интегрирование интерполирующих полиномов При заменеf(x) интерполирующим полиномом() ()()() ()()()()1110010,,1 ,,,0,1,..., ipipipnipxxp iiiijijjxxxbxmmiiaxxp iijijipipi IfxdxPxdxPxcxn IIfxdxPxdxmp fxPxcxxxximϕ+++====+= =≈= ==≈=− ≈=∈= ∑ ∫∫ ∑∑ ∫∫∑ Интегрирование интерполирующих полиномов При заменеf(x) интерполирующим полиномом()10,1ipxppmmx ijijijijx ijijxmi IcxdxcxdxnImpϕ+ ===== ==Φ= ==− ∑∑∑∑∫∑ Интегрирование интерполирующих полиномов Формулы прямоугольников:
• левосторонних;
• правосторонних;
• центральных.xixi12iixx+yiyi12iixxf+ ÷ Формула левосторонних прямоугольников На отрезке[xi,xi+1] полагаемp =1,Pi(x) =yi.
Получаем: Для равномерной сетки()1011001,nixnnxiiixiix iiii Ifxdxyxyh hxxx+ −−==+ =≈= =∆=− ∑∑∫()010nxnix Ifxdxhy−= =≈∑∫ Формула левосторонних прямоугольниковyx… a = x0x1x2x3xn –1xn = by0y1y2yn –1 Формула правосторонних прямоугольников На отрезке[xi,xi+1] полагаемp =1,Pi(x) =yi+1.
Получаем: Для равномерной сетки()1011001,nixnnxiiixiix iiii Ifxdxyxyh hxxx+ −−++==+ =≈= =∆=− ∑∑∫()001nxnniix Ifxdxhyhy−+== =≈= ∑∑∫ Формула правосторонних прямоугольниковyx… a = x0x1x2x3x n–1y3y1y2ynxn = b Формула центральных прямоугольников На отрезке[xi,xi+1] полагаемp =1, Получаем:()10110022nixnnx iiiiixiix xxxx Ifxdxfxfh+ −−++==++ =≈= ÷÷ ∑∑∫()0102nxniiixxx Ifxdxhf−+=+ =≈ ÷ ∑∫()12iiixxPxf+ = ÷ Формула трапеций На отрезке[xi,xi+1] полагаемp =1,()1iiiiiiyy Pxxxyh+− =−+()121212122iiiiiiixii iiiiiiixyy PxdxxxyxChyy IxxyxCyyhh+− =−++⇒ − ⇒=−++=+ ÷ ∫ Формула трапеций На отрезке[a,b] Для равномерной сетки()111 100110011122nnn iiiiiiinniii IIhyyyhyhhyh −−− +−−=== ==+=+++ ÷ ∑∑∑()111001222nn iiiniihh Iyyyyy −−+== =+=++ ÷ ∑∑ Формула трапецийyx… a = x0x1x2x3x n–1y3y1y2ynxn = byn –1y0 Квадратурные формулы Вспомним формулу Выполним подстановку:() ()()110, ipipxxp iiiijijjxx IfxdxPxdxPxcxϕ++= =≈=∑ ∫∫()1(1)00ip ipipxpp iijijijijjjxx Icxdxcxdx ϕϕ+== ÷ ≈= ÷ ∑∑ ∫∫ Квадратурные формулы Если предположить, чтоcij =yip+j⋅Cij , то гдеAij – квадратурные коэффициенты.
Тогда ()() (1)(1)0, ipipxxpp iijijipjijijjjxxp ijipjj IcxdxyCxdxAy ϕϕ+++==+= ÷÷ ≈=×= ÷÷ = ∑∑ ∫∫∑000,1.pmm iijipjiijn IIAymp+=== ===− ∑∑∑ Квадратурные формулы ЕслиPi(x) =Lp,i(x) , т.е.
то ()(),0,pipk ppiipjjk ipjipkkjxx PxLxyxx+=++≠ − ÷== ÷− ÷ ∑∏()001,.pp ijijipkkk ipjipk kjkj Cxxxxxϕ+==++ ≠≠ ==−− ∏∏ Квадратурные формулы Тогда Дляp= 1 имеем:() (1)(1)001 ipipxxpp ijijijipkjj ipjipkxx jkjk ACxdxxxdxxxϕ+++==++ ≠≠ ==−− ∏∏ ∫∫ ()()1 11,111iiiii iiii xxxx PxLxyy xxxx+++ −−==+ −− ()() 0101111,,, iiiiii iiii CCxxxxxx xxxx ϕϕ+++ ===−=− −− Квадратурные формулы Интегрируем:()12121221112110;22110222ixiiiiiixiiiiiiiixiiiiiixxx Axxdxxxhxxh Axxdxhxx xxxxhhh+− =−=−=− − =−−==−= ÷− −− ==−= ÷ ∫ Квадратурные формулы В итоге Получили формулу трапеций.()11,222iii iiiiihhh Iyyyy++ =+=+()10012mn iiiiii IIhyy−+====+ ∑∑11,1nmn =−== Квадратурные формулы Дляp= 2 имеем: ()() 2122 22,2 221222 222221 2122 21221222222221ii iiiiii iiiiiiii xxxx PxLxy xxxx xxxxxxxxyy xxxxxxxx++ ++++++ −−==+ −− −−−−++ −−−− ()() ()()() ()() ()()() ()() ()()() 002122 221222 11222 2122122 21221 22222211,,1,,1,, iiii Cxxxxx xxxx Cxxxxx xxxx Cxxxxx xxxxϕ++++++++++ ==−− −− ==−− −− ==−− −− Квадратурные формулы Интегрируем: и т.д.
()()()222222 02122 2212222 21222122 22122122212126ixiii iiiix iiiiiiixiii Axxxxdx xxxx xxxxxxdxhhhhhh+++ +++++ =−−= −− =−++= −−−+ =−∫ Квадратурные формулы В итоге получим: Это формула Симпсона: ()()() ()()3 21222121201 2212 2122122212,,6626 iiiiiiiiiii iiiii hhhhhhAAhhh hhhhAh+++++++ +−+== +−= ()()(())2212 21221221221212 221222262ii iiiiiiiiii iiiihh Ihhhyhhyhh hhhy+ ++++++++ =−+++ +− Квадратурные формулы Для отрезка[a,b] ()()(())2212 212212212210212 221222262,12mii iiiiiiiiii iiiihh Ihhhyhhyhhn hhhym+ ++++=++++ =−+++ +−=−∑ Квадратурные формулы Если сетка равномерная, то т.е.
коэффициентыAj не зависят от индексаi .
Для отрезка[a,b]000,1.pmm ijipjiijn IIhAymp+=== ===− ∑∑∑()110.
ipipipxp iipjipjjxip IPqdxhPqdqhAy+++====∑ ∫∫ Квадратурные формулы Интерполирующий полином т.е.
()()()()01!!ppjjppjkkjy PqLqqkjpj−=≠ ÷ ==−− ÷− ÷ ∑∏() ()()01,!!pjpjjkkj Cqqkjpjϕ−=≠− ==−−∏ Квадратурные формулы Тогда()001!!ppjpjjjkkj ACqdqqkdqjpjϕ−=≠− ==−−∏ ∫∫ Коэффициенты Ньютона- Котеса В случае равномерной сетки положим ЗдесьHi – коэффициенты Ньютона- Котеса .
Т.е.1.jjHAp=()01!!pjpjkkj Hqkdq pjpj−=≠− =−−∏∫ Коэффициенты Ньютона- Котеса Свойства коэффициентов Ньютона- Котеса:01);
2)1.jpjpjHHH−=∑ Примерыn = 6i 0123456x 01/91/419/449y 01/31/213/223 012345 111151395 0;;1;1;
994936444497 4;94544 hhhhhh =−==−==−==−= =−==−= Примеры Левосторонние прямоугольники:i 0123456x 01/91/419/449y 01/31/213/223h 1/95/363/45/47/4550 11513537 0125 933624424386 14.296327iiiIyh= ==×+×+×+×+×+×= =≈∑ Примеры Правосторонние прямоугольники:i 0123456x 01/91/419/449y 01/31/213/223h 1/95/363/45/47/45510 11153357 1235 392364244 2293 21.2315108iiiIyh+= ==×+×+×+×+×+×= =≈∑ Примеры Трапеции:i 0123456x 01/91/419/449y 01/31/213/223h 1/95/363/45/47/45()510 11115113101 2293363242 53731297 1252317.7639 424372iiii Ihyy+= =+=×++×++×++ ÷÷÷ ×++×++×+=≈ ÷÷÷ ∑ Примеры Формула Симпсона:i 0123456x 01/91/419/449y 01/31/213/223h 1/95/363/45/47/45 ()()(())2212 212212212210212 22122226 53619515220 65361936936 51115112 369393692ii iiiiiiiiii iiiihh Ihhhyhhyhh hhhy+ ++++=++++ =−+++ + +−=××−×+ ÷ ×× ++×+××−×+÷ ÷÷÷ ∑ Примеры Формула Симпсона:2 543453515321 65434444244 353357473 2525 4442657442 77791211 5225518.0974 4445040+ +××−×++×+ ÷÷ ×× + +××−×+××−×+ ÷÷ ÷ ×× ++×+××−×=≈ ÷÷÷ Примеры Точность интегрирования:IδI ЛП 14.296320.6%I ПП 21.231517.9%IТ 17.76391.31%IС 18.09740.54%9018































 Математика
Математика








