Похожие презентации:
Дифференциальное исчисление функции нескольких действительных переменных. Тема 3.3
1. Тема 3.3.Дифференциальное исчисление функции нескольких действительных переменных.
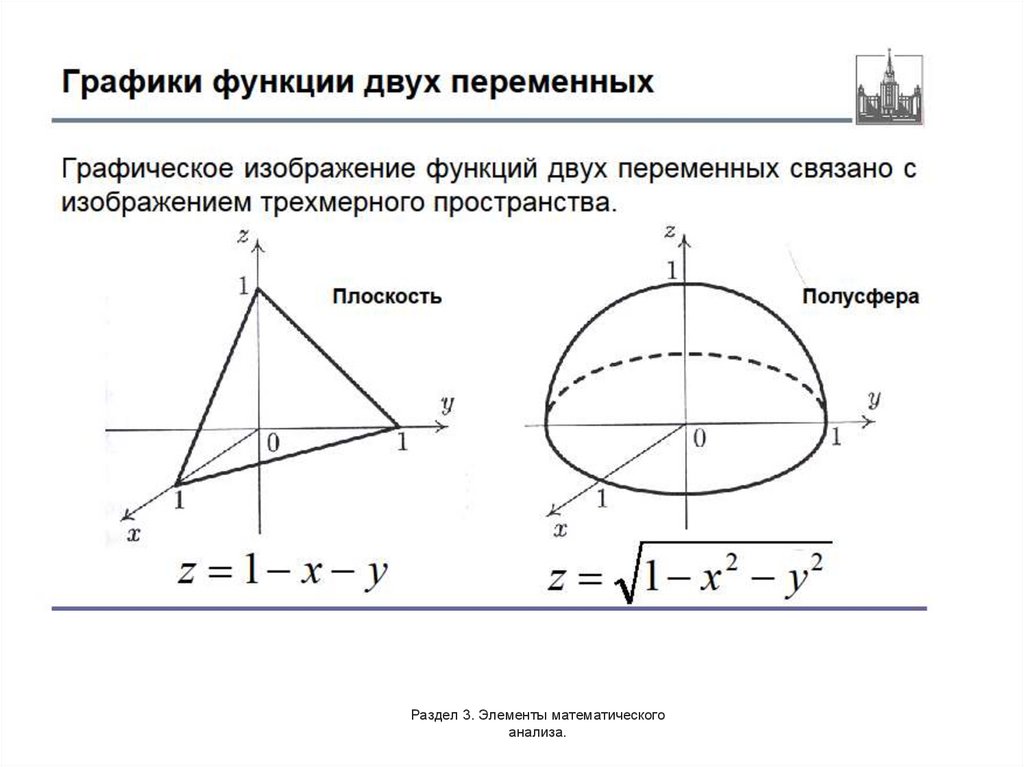
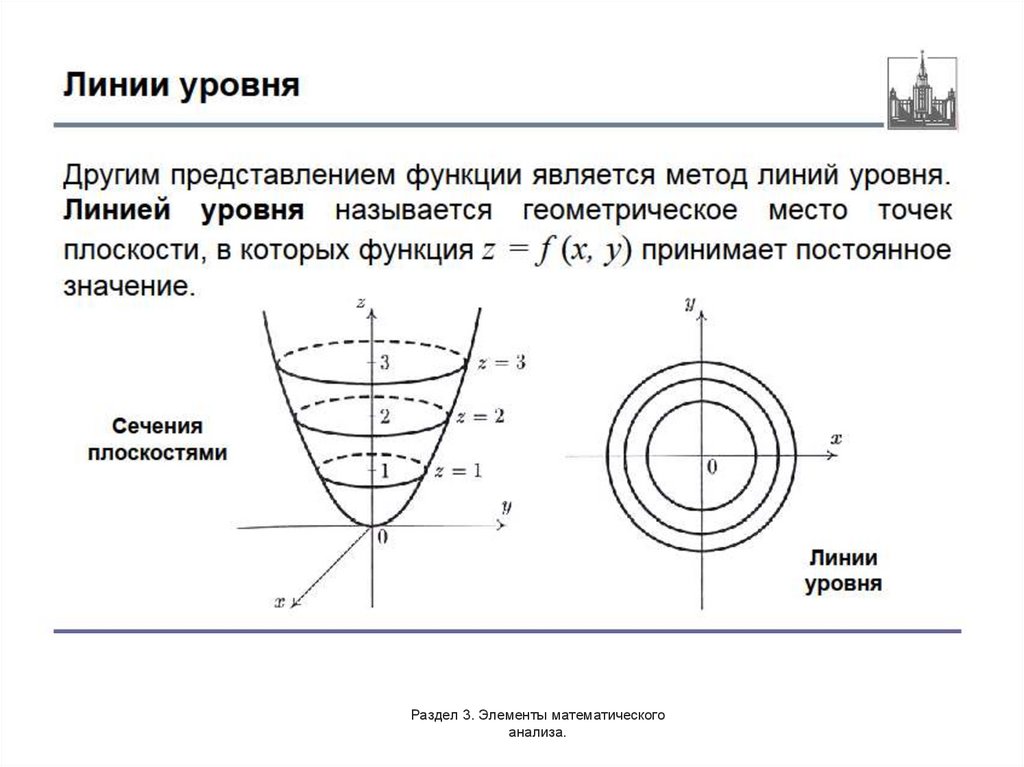
Функции нескольких переменных: основныепонятия.
1.
Определение ФНП.
2.
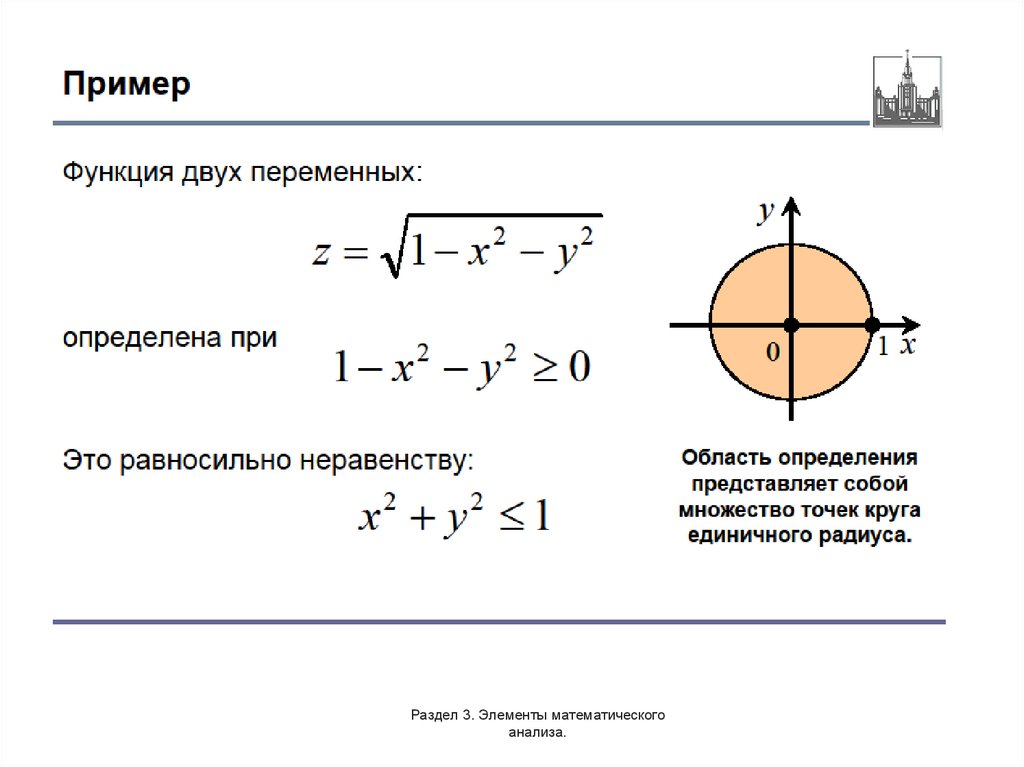
Примеры.
Глава 11, стр. 179-180
В.С.Шипачёв Задачник по высшей математике.
Раздел 3. Элементы математического
анализа.
2.
Раздел 3. Элементы математическогоанализа.
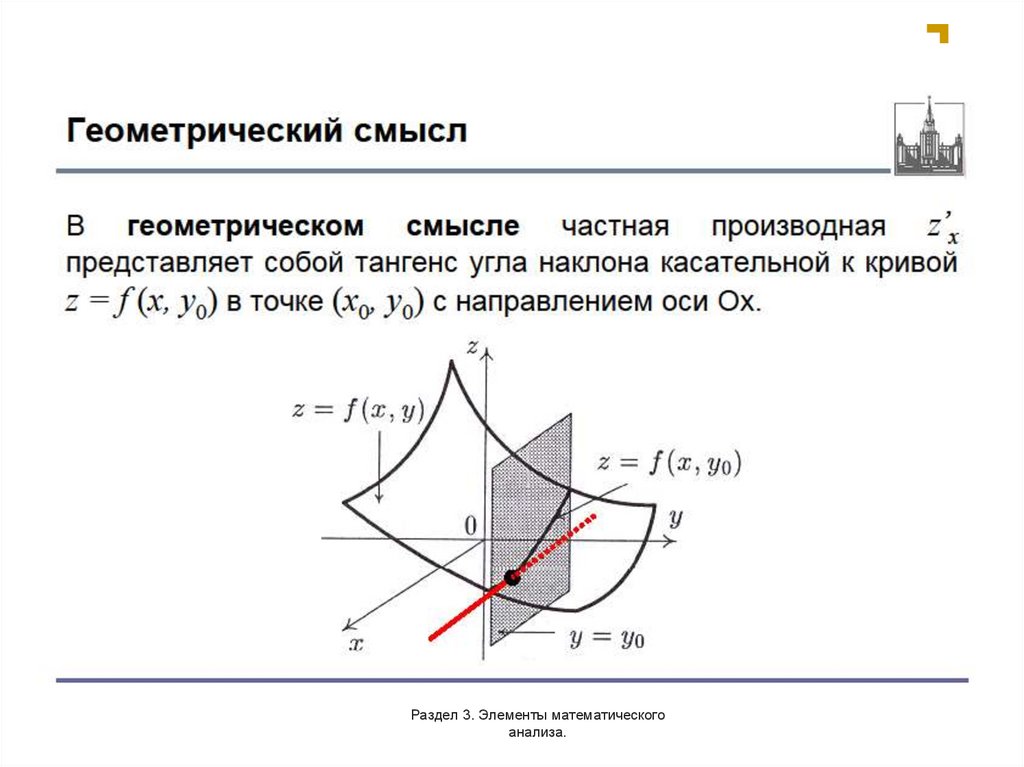
3. Частные производные и дифференцируемость ФНП
Задание:1. Изучить теоретический материал
глава 12 п.1 стр. 184-185+
презентация
2. Выписать основные определения.
3. Разобрать пример стр. 185.
Раздел 3. Элементы математического
анализа.
4.
Раздел 3. Элементы математическогоанализа.
5.
Раздел 3. Элементы математическогоанализа.
6.
Раздел 3. Элементы математическогоанализа.
7.
Раздел 3. Элементы математическогоанализа.
8.
Раздел 3. Элементы математическогоанализа.
9.
Раздел 3. Элементы математическогоанализа.
10.
Раздел 3. Элементы математическогоанализа.
11.
Раздел 3. Элементы математическогоанализа.
12.
Раздел 3. Элементы математическогоанализа.
13.
Раздел 3. Элементы математическогоанализа.
14. Дифференциал функции. Градиент.
ДифференциалГрадиент.
функции.
Задание:
1. Изучить теоретический материал
глава 12 п.3 стр. 188+ презентация
2. Выписать определение, формулу.
3. Разобрать пример 3 стр. 189-190
Раздел 3. Элементы математического
анализа.
15.
Раздел 3. Элементы математическогоанализа.
16.
Раздел 3. Элементы математическогоанализа.
17. Градиент функции
Градиентом функции z=f(M) в точкеМ(x,y) называется вектор ,
координаты которого равны
соответствующим частным
производным
/
/ ,
zx , z y
взятым в точке М(x,y).
Раздел 3. Элементы математического
анализа.
18. Градиент функции
Обозначение:grad z z ; z
/
x
Раздел 3. Элементы математического
анализа.
/
y
19. Проверочная работа
«Дифференциал функциинескольких переменных.
Градиент».
Раздел 3. Элементы математического
анализа.















 Математика
Математика








