Аналитическая геометрия. Аналитическое представление линии и поверхности в пространстве

1. Курс высшей математики

Часть 1
УГТУ-УПИ
2004г.

2.

Лекция 5
Аналитическая геометрия
1. Аналитическое представление линии и
поверхности в пространстве .
2.Плоскость в пространстве.
3. Прямая в пространстве.

3.

1.
Аналитическое представление линии и
поверхности в пространстве.
Задачей аналитической геометрии является изучение
геометрических объектов аналитическими методами,
то есть средствами алгебры и математического анализа,
без геометрических построений.
Геометрические объекты: точка,линия,поверхность,
тело.

4.

В основе аналитической геометрии лежит метод
координат , позволяющий описывать положение точки
в пространстве с помощью чисел (координат точки),
что и обеспечивает возможность привлечения методов
алгебры и анализа .
Из всех используемых при этом систем координат
наиболее часто применяется декартова система –
совокупность
r r rточки О и ортонормированного
базиса i , j , k , OX, OY , OZ - координатные оси.

5.

Z
k
O j
i
Точку М можно задать вектором
M
Y
r
r uuuu
rM OM
rM x, y , z
X
Декартовыми координатами точки М
называются декартовы координаты её радиусвектора
rM x, y , z M ( x, y , z )

6.

Более сложные геометрические объекты задаются
уравнениями (или неравенствами), связывающими
координаты точек, образующих эти объекты.

7.

Линия на плоскости .
Уравнение вида Ф(x,y) = 0 называется уравнением
линии L на плоскости, если ему удовлетворяют
координаты x и y любой точки M(x,y) лежащей на
этой линии и не удовлетворяют координаты ни
одной точки не лежащей на этой линии.
.

8.

Линия L - геометрическое место точек,
удовлетворяющих уравнению Ф(x,y)=0.
Пример.
2
2
2
x y r 0
O
r
A
A ( r ,0 ) L
O(0,0) L

9.

Поверхность в пространстве .
Пусть
S
- некоторая поверхность.
Уравнение вида Ф(x,y,z)=0 называется уравнением
этой поверхности,если ему удовлетворяют координаты
любой точки M(x,y,z) лежащей на этой поверхности и
не удовлетворяют координаты ни одной точки, не
лежащей на этой поверхности.

10.

Поверхность S - геометрическое место
точек, координаты которых удовлетворяют
уравнению Ф(x,y,z)=0.
Пример:
x y z r 0
2
2
2
2

11.

Линия в пространстве .
Кривую в пространстве можно рассматривать как
линию пересечения двух поверхностей, то есть как
геометрическое место точек, принадлежащих обеим
поверхностям.

12.

Следовательно, координаты этих точек должны
удовлетворять системе уравнений :
1 ( x, y, z ) 0,
2 ( x, y, z ) 0.
(Здесь Ф1(x,y,z)=0 и Ф2(x,y,z)=0 – уравнения
пересекающихся поверхностей).

13.

Пример. Окружность – линия пересечения сферы и
плоскости:
y
x 2 y 2 z 2 4,
z 1
2
1
0
-1
-2
2
1
z
0
-1
-2
-2
-1
x
0
1
2

14.

Параметрические уравнения линии и поверхности .
При параметрическом задании линии L, её можно
рассматривать как траекторию движения точки
M(x,y,z):
x x t
L : y y t , t – параметр, играющий роль
времени.
z z t
Уравнения задают положение точки в каждый момент
времени.

15.

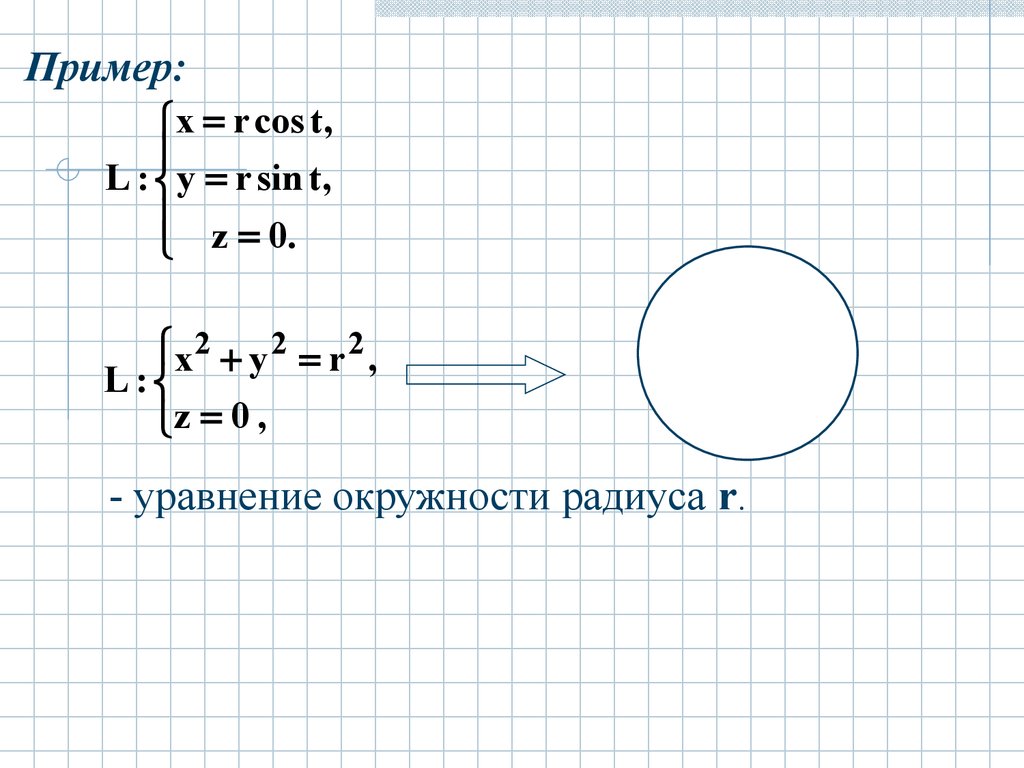
Пример:
x r cos t ,
L : y r sin t ,
z 0.
x 2 y 2 r 2 ,
L:
z 0 ,
- уравнение окружности радиуса r.

16.

Для параметрического задания поверхности S
необходимы два параметра – u и v :
x x (u , v ),
S:
y y (u , v ),
z z (u , v ).

17.

Пример. Уравнение сферы радиуса R:
sin cos ,
x Rф
S : y Rф
sin sin ,
z R cos .

18.

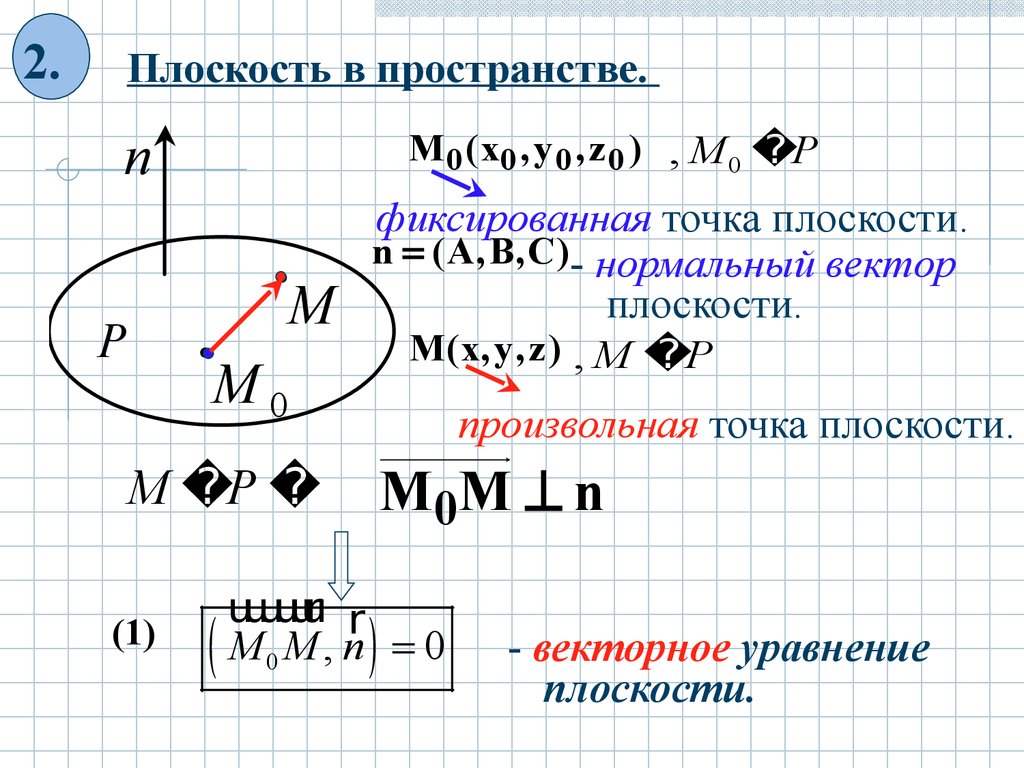
2.
Плоскость в пространстве.
n
P
M 0 ( x0 , y 0 , z 0 ) , M 0 P
M
фиксированная точка плоскости.
n ( A , B, C) - нормальный вектор
плоскости.
M( x, y , z ) , M P
M0
произвольная точка плоскости.
M 0M n
M P
(1)
uuuuuu
r r
M 0M , n 0
- векторное уравнение
плоскости.

19.

M 0M x x 0 , y y 0 , z z 0 ;
( 2)
n A , B, C
A( x x0 ) B( y y 0 ) C( z z 0 ) 0
- уравнение плоскости, проходящей через
точку
M0(x0,y0,z0) перпендикулярно вектору n A, B, C .
( 3) Ax By Cz D 0
D Ax0 By 0 Cz 0
- общее уравнение плоскости.

20.

( 4)
x y z
1
a b c
D
D
D
a , b , c
A
B
C
- уравнение плоскости «в отрезках».
Здесь P1(a,0,0), P2(0,b,0), P3(0,0,c) – точки
пересечения плоскости с координатными осями,
a, b, c - «отрезки», отсекаемые плоскостью на
z
координатных осях.
p3
c
a
x
p1
b
p2
y

21.

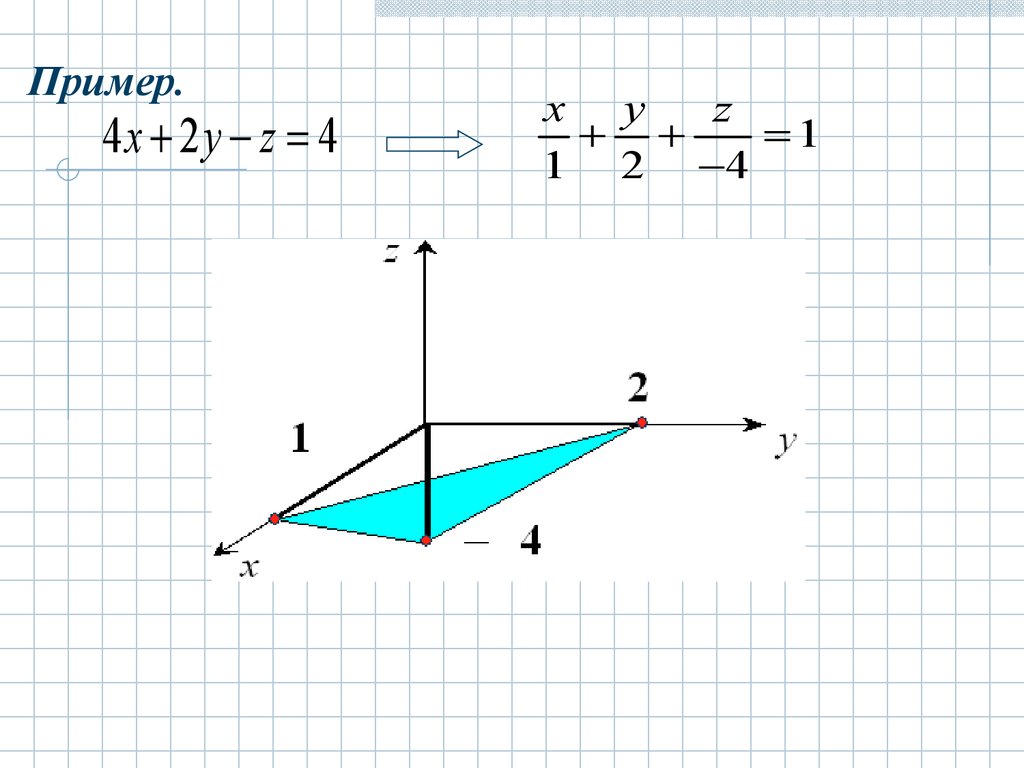
Пример.
4x 2 y z 4
x y
z
1
1 2 4

22.

Угол между двумя плоскостями .
Рассмотрим
P1 : A1 x B1 y C1 z D1 0, n1 A1 , B1 , C1
P2 : A2 x B2 y C2 z D2 0, n 2 A 2 , B 2 , C2
cos cos n1 , n 2
A1A 2 B1B 2 C1C2
A12 B12 C12 A 22 B 22 C22

23.

Условие перпендикулярности двух плоскостей.
P1 P2
A1A 2 B1B 2 C1C2 0
Условие параллельности двух плоскостей.
P1 P2
A1 B1 C1
A 2 B 2 C2

24.

3. Прямая в пространстве.
M
M0
L
a
M 0 ( x0 , y 0 , z 0 ) -фиксированная точка прямой , M 0 L
a (l, m, n )
- направляющий вектор прямой , a || L
M ( x, y , z )
- произвольная точка прямой
M L M 0M || a
uuuuuur r
M 0 M ta
(1)

25.

(1) - векторное уравнение прямой.
uuuuuu
r
r
M 0 M x x0 , y y0 , z z0 , a l , m, n
x x0 y y0 z z0
l
m
n
2
M 0M || a
- канонические уравнения прямой.
3
x x0 lt ,
y y0 mt ,
z z0 nt
- параметрические
уравнения прямой.

26.

(4)
A1x B1y C1z D1 0,
A 2 x B 2 y C2 z D2 0
- общие уравнения прямой.
Эти уравнения определяют прямую как линию
пересечения двух не параллельных плоскостей .

27.

Угол между двумя прямыми
ur uu
r
a1 , a2
cos ur uu
r
a1
a2
Если
ur
uur
a1 (l1 , m1 , nи
l ( m2 , n2 , 2 ) направляющие векторы
1) a
2
прямых L1 и L2 , то угол межу прямыми равен
cos
l1l 2 m1m 2 n1n 2
l12 m12 n12 l 22 m 22 n 2 2

28.

Угол между прямой и плоскостью.
Пусть
r
n A, B, Cнормальный
вектор плоскости
r
a l , m, nнаправляющий
вектор прямой
sin
Al Bm Cn
A 2 B 2 C2 l 2 m 2 n 2
L
.
.

29.

Условие параллельности двух прямых.
L1 || L 2 a1 || a 2
l1 m1 n1
l2 m2 n2
Условие перпендикулярности двух прямых.
L1 L 2 a1 a 2 l1l 2 m1m 2 n1n 2 0

30.

Условие параллельности прямой и плоскости.
L || P a n Al Bm Cn 0
Условие перпендикулярности прямой и плоскости.
L P
a || n
l m n
A B C

31.

Условие скрещиваемости двух прямых.
Две прямые называются скрещивающимися, если
они не лежат в одной плоскости.
Если M1 L1 , M 2 L 2 , L1 L 2
a2
M1M 2 a1 a 2 0
L2
M2
a1
L1
M1

32.

МКТ 7
1. Записать координаты нормального вектора
плоскости
2x 4y 3z 6 0.
2. Какое произведение векторов использовано
в условии ортогональности двух плоскостей
A1A 2 B1B 2 C1C2 0.

33.

3. Какой объект описывает система
A1x B1y C1z D1 0,
A 2x B 2y C2z D2 0.
4. Указать взаимное расположение плоскостей
2x+y-z+5=0, x-2y-1=0.