Взаимное пересечение поверхностей. Лекция № 7

1.

Взаимное пересечение
поверхностей

2.

Кадр 2
ВВЕДЕНИЕ
Конструктивные формы различных изделий
часто представляют собой сочетание
поверхностей различной конфигурации:
призмы, пирамиды, цилиндры, сферы,
конусы и т.д., которые пересекаясь между
собой образуют линии перехода или
пересечения.
Поэтому в процессе их разработки у
конструкторов, архитекторов, дизайнеров
и т.п. возникает необходимость заранее
предусматривать
характер
линий
перехода (пересечения) и решать вопрос,
с какой точностью эти линии должны
быть изготовлены.
Для того, чтобы ответить на эти вопросы
выполняется
геометрически
точное
построение линий перехода – линии
пересечения поверхностей.
В общем случае линия пересечения может
иметь
вид
плоской
кривой,
пространственной кривой или ломаной
линии.
Рисунок 1

3.

Кадр 3
Конфигурация линии пересечения определяется формой
пересекающихся
поверхностей
и
их
расположением
относительно друг друга.
Пересечение
поверхностей
многогранников
(призм,
пирамид)
дает
ломаные
линии,
отрезки
которых
являются
линиями
пересечения
соответствующих граней.
Пересечение поверхностей тел
вращения
(цилиндров,
конусов,
сфер
и
др.)
образует в общем случае
пространственные кривые,
а в частных случаях –
плоские линии пересечения
(эллипс, окружность) или
прямые линии.

4.

Кадр 4
Варианты взаимного пересечения двух поверхностей:
1– врезка
линия
пересечения - одна
замкнутая
пространственная
линия;
2 – полное пересечение
(проницание)
линия пересечения
распадается на две замкнутые
пространственные линии –
линии входа и выхода одного
тела из другого;
1
2
Рисунок 2

5.

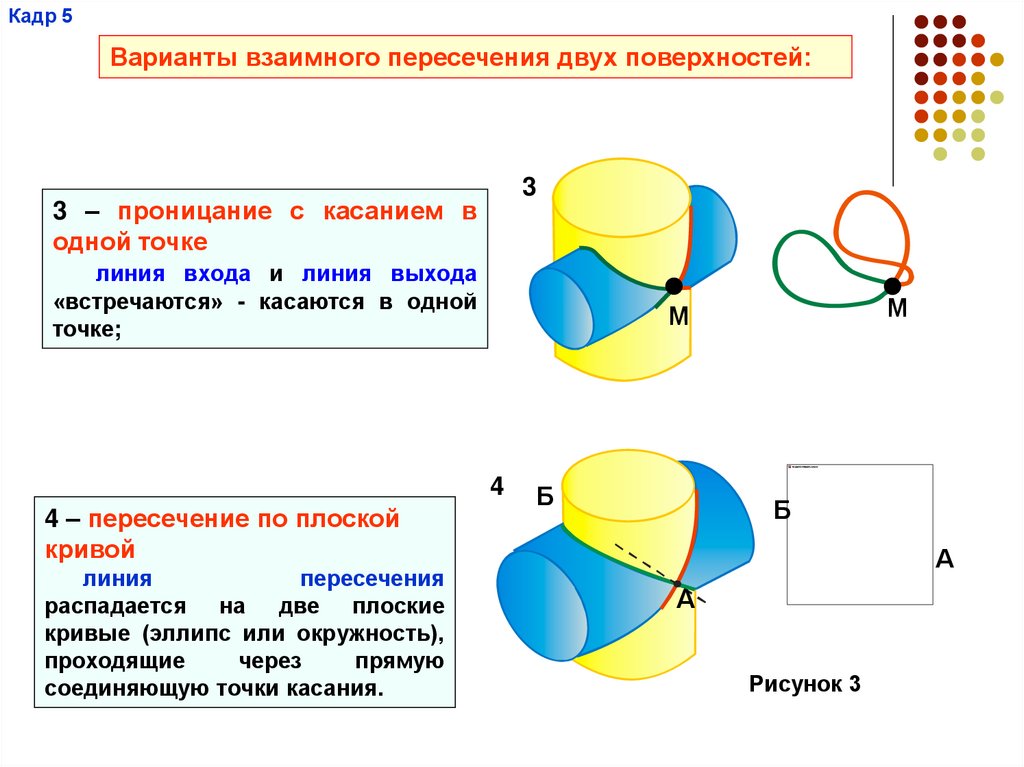
Кадр 5
Варианты взаимного пересечения двух поверхностей:
3
3 – проницание с касанием в
одной точке
линия входа и линия выхода
«встречаются» - касаются в одной
точке;
4
4 – пересечение по плоской
кривой
линия
пересечения
распадается на две плоские
кривые (эллипс или окружность),
проходящие
через
прямую
соединяющую точки касания.
М
М
Б
Б
А
А
Рисунок 3

6.

Кадр 6
Последовательность
решения задач
Последовательность решения задач:
На практике существует несколько методов построения линии
пересечения поверхностей, которые применяются в зависимости от
формы геометрических тел, их расположения относительно друг
друга и относительно плоскостей проекций.
Одним из наиболее распространенных методов является способ
вспомогательных секущих плоскостей уровня.
Независимо от вида поверхностей и варианта их пересечения существует
общая последовательность решения задач данного типа:
1. Проанализировать форму геометрических поверхностей и их
расположение относительно друг друга и относительно
плоскостей поверхностей.
2. Определить вариант пересечения поверхностей и характер
получаемой линии пересечения.
3. Найти опорные точки линии пересечения,
4. Построить промежуточные точки линии пересечения.
5. Построить искомую линию пересечения.
6. Определить видимость участков линии пересечения.

7.

Кадр 7
Способ вспомогательных секущих плоскостей
Способ заключается в том, что при пересечении пересекающихся
поверхностей некоторой плоскостью
(рис. 4), получаются как бы
отдельные линии пересечения плоскости с каждой поверхностью. В свою
очередь, точки пересечения этих линий являются общими для заданных
поверхностей. На рисунке 4,а- это точки М и N.
Если построить не одну плоскость, а несколько плоскостей посредников, то образуется целая группа взаимно общих точек, через
которые и будет проходить искомая линия пересечения поверхностей. На
рис. 4,б показано, как через точки 1,2,3,4 проходит передняя половина
линии пересечения цилиндра и полусферы.
а
б
Рисунок 4

8.

Кадр 8
Способ вспомогательных секущих плоскостей
При построении линии пересечения сначала находят так
называемые опорные точки:
Очевидные – определяемые без дополнительных графических построений;
Характерные – лежащие на очерковых образующих поверхностей вращения
(цилиндрических, конических и др.) или на крайних ребрах многогранных
поверхностей. Эти точки позволяют в дальнейшем определить видимость
участков линии пересечения.
К характерным точкам относятся также крайние точки линии пересечения:
самые высшие, низшие, правые и левые.
Все остальные точки линии пересечения называются промежуточными.
Для построения промежуточных точек применяются взаимно параллельные
вспомогательные секущие плоскости. В качестве вспомогательных
плоскостей наиболее часто применяют плоскости уровня. При этом их
выбирают так, чтобы они пересекали заданные поверхности по простым
линиям – прямым или окружностям.
Важно отметить, что перед тем как строить линию пересечения на чертеже
необходимо хотя бы приблизительно представить ее в пространстве!!!

9.

Кадр 9
Задача:
Построить
линию
пересечения
четырехгранной призмы с полуцилиндром (рис.5,6).
прямой
1. Вид заданных поверхностей –
полуцилиндр и прямая четырехгранная призма.
Анализируем взаимное расположение поверхностей
относительно друг друга
– полуцилиндр лежит в горизонтальной плоскости, его
основания
параллельны
профильной
плоскости
проекций,
– призма перпендикулярна горизонтальной плоскости и
располагается в центре полуцилиндра (плоскости
симметрии поверхностей совпадают).
2. Определяем вариант пересечения поверхностей и
характер получаемой линии пересечения –
Вариант пересечения – врезка.
Линия пересечения - замкнутая пространственная
линия, участки которой представляют собой отрезки
эллипса.
3. Определяем опорные точки. Грани призмы
пересекают цилиндрическую поверхность по линиям,
которые
замыкаются между собой в точках входа ребер призмы в
цилиндр (опорные точки A,B,C,D).
Рисунок 5
C – на скрытой от наблюдателя стороне
B
A
D
Рисунок 6

10.

Кадр 10
Порядок построения
1. Строим горизонтальные проекции
опорных точек А,В,С, D.
′ ′ С′ D′- горизонтальная
проекция линии пересечения
2. Строим профильную проекцию
линии пересечения- ′′′(B′′′) C′′′ D′′′.
3. Построение промежуточных точек
линии пересечения.
Для построения промежуточных
точек проводим вспомогательные
секущие фронтальные плоскости
уровня , (их горизонтальные
проекции ′ и ′ - прямые линии).
Получаем проекции точек M′, N′, K′,
L′. Используя линии связи строим
M′′′N′′′K′′′L′′′.
4. Строим фронтальную проекцию
линии пересечения- M′′N′′K′′L′′.
5. Определение видимости линии
пересечения.
Так как поверхности полусферы и
призмы
имеют
совпадающие
плоскости симметрии, то и отрезки
линии пересечения на передней и
задней
сторонах
геометрической
фигуры совпадают, т.е. невидимая
часть линии спрятана точно за
видимыми отрезками.
′′ ′′ ′′
′′
′′ L′′
D′′(C′′
′
С′
′
′
′
′
L′
′
′
D′
С′′′
′′′ L′′′ ′′′(B′′′)
′′′ ′′′
D′′′

11.

Кадр 11
Задача: Построить линии пересечения цилиндров 1 и 2
1.Определяем вид заданных поверхностей- 1-цилиндр,2-цилиндр,111-цилиндр
2. Анализируем взаимное расположение поверхностей относительно друг друга
– ось цилиндра I параллельна горизонтальной плоскости, его основания перпендикулярны
профильной плоскости проекций,
– оси II и III цилиндров перпендикулярны горизонтальной плоскости
II
′′
3.
Определяем
вариант
пересечения
поверхностей и характер получаемой линии
пересечения –
– I и II цилиндры – врезка, линия пересечения замкнутая пространственная линия,
– I и III цилиндры – пересечение по двум
плоским кривым - половинам эллипсов.
′′ ′′
′′ L′′
′′
D′′(C′′
I
4. Порядок построения:
4.1 Построение линии пересечения I и II
цилиндров
- Определяем проекции опорных точек
A,B,C,D:
- Строим проекции промежуточных точек
M,N,K,L,
для этого выбираем вспомогательные секущие
фронтальные плоскости уровня , (их
горизонтальные проекции ′ и ′ - прямые линии).
Соединяя последовательно найденные точки на
всех проекциях, получаем проекции линии
пересечения поверхностей.
′′′(B′′′)
′′′ L′′′
′′′ ′′′
С′′′
D′′′
III
′
′
′
С′
L′
′
′
′
D′
′

12.

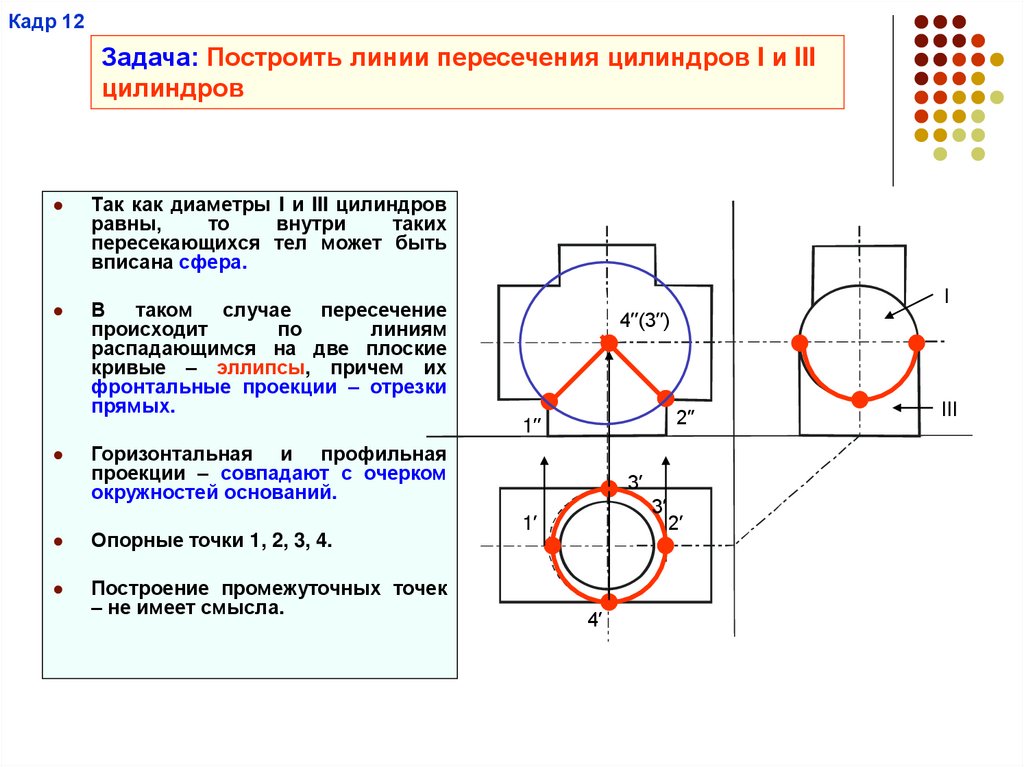
Кадр 12
Задача: Построить линии пересечения цилиндров I и III
цилиндров
Так как диаметры I и III цилиндров
равны,
то
внутри
таких
пересекающихся тел может быть
вписана сфера.
В таком случае пересечение
происходит
по
линиям
распадающимся на две плоские
кривые – эллипсы, причем их
фронтальные проекции – отрезки
прямых.
I
4′′(3′′)
2′′
1′′
Горизонтальная и профильная
проекции – совпадают с очерком
окружностей оснований.
Опорные точки 1, 2, 3, 4.
Построение промежуточных точек
– не имеет смысла.
3′
3′
1′
4′
2′
III

13.

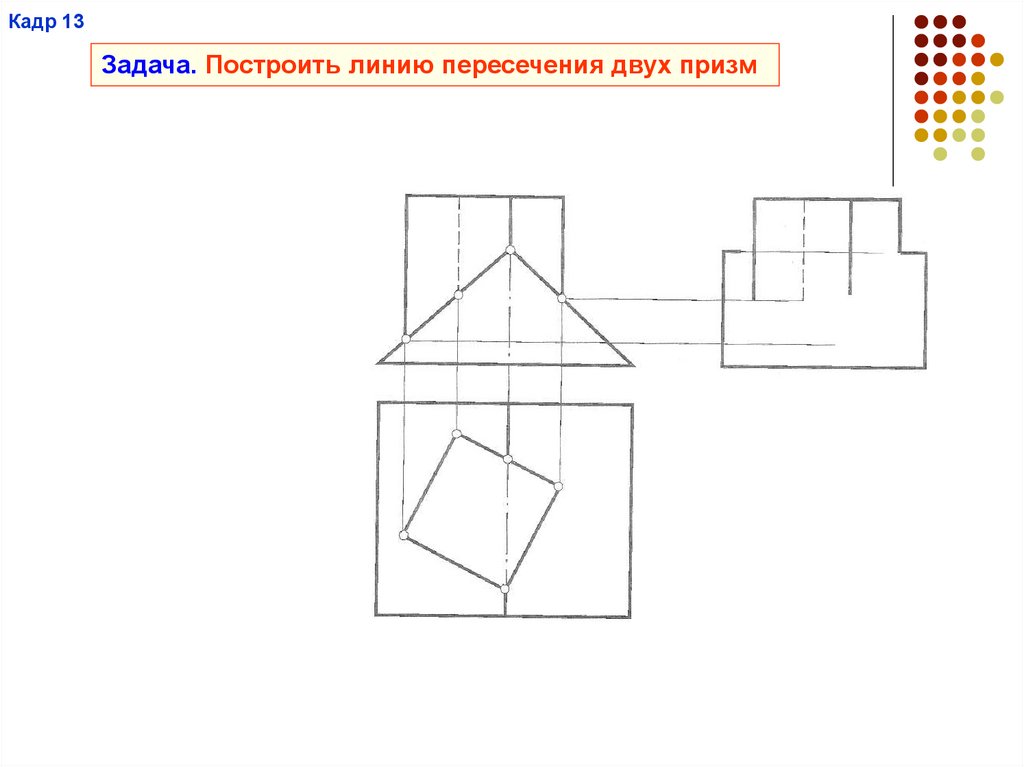
Кадр 13
Задача. Построить линию пересечения двух призм

14.

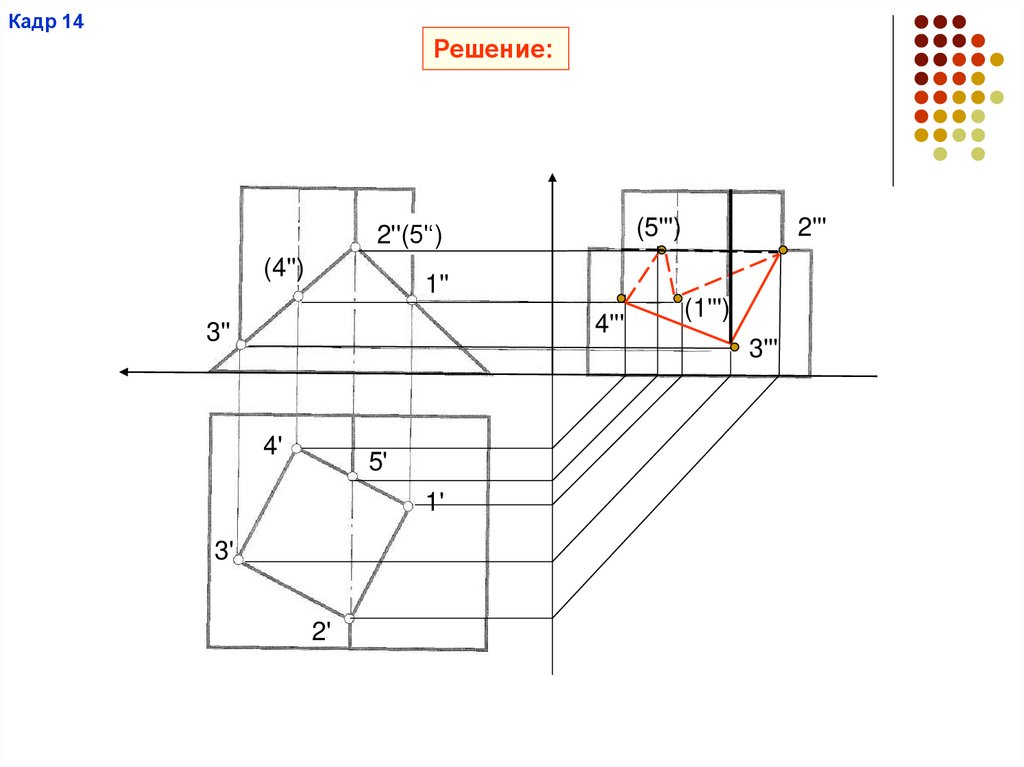
Кадр 14
Решение:
(5''')
2''(5'‘)
(4'')
2'''
1''
4'''
3''
(1''')
3'''
4'
5'
1'
3'
2'