Похожие презентации:
Кусочно-заданные функции. 9 класс
1. Функции.
Рябинина Л.А.2. Кусочно-заданные функции.
щелкните3. ОПРЕДЕЛЕНИЕ.
• Кусочно-заданная функция —функция, определённая на
множестве вещественных чисел
заданная на каждом из интервалов,
составляющих область определения,
отдельной формулой.
4. Формальное определение и задание функции.
• Пусть заданы x1 x2 x3 ... xn— точкисмены формул.
• Кусочно-заданные функции, обычно задают
на каждом из интервалов ( ; x1 ), ( x1; x2 )...( xn ; )
отдельно .
• Записывают это в виде:
5. Запись кусочно-заданной функции.
f 0 ( x ), x x1,f (x)=
f1 ( x ), x1 x x2 ,
...
f n ( x ), xn x .
6. Виды кусочно-заданных функций
• Если все функции — постоянные, то f(x) — кусочно-постояннаяфункция.
• Если все функции fi(x) являются линейными функциями, то f(x) —
кусочно-линейная функция.
• Если все функции fi(x) являются непрерывными функциями,
то f(x) — кусочно-непрерывная функция. При этом сама она
может не являться непрерывной.
• Если все функции fi(x) являются дифференцируемыми
функциями, то f(x) —кусочно-гладкая функция. При этом точки
смены формул могут быть (а могут и не быть) точками излома.
• Если все функции fi(x) являются монотонными функциями,
то f(x) —кусочно-монотонная функция. При этом на соседних
интервалах монотонность может быть разной.
7. Построение графиков кусочно-заданных функций.
Построение графиков кусочнозаданных функций.• f(x)=
х
x=0 -является точкой смены формул.
x, x 0,
f ( x)
x, x 0.
8.
f(x)=-xУ
f(x)= x
x 0
x 0
0
Х
1
x, x 0,
f ( x)
x, x 0.
9.
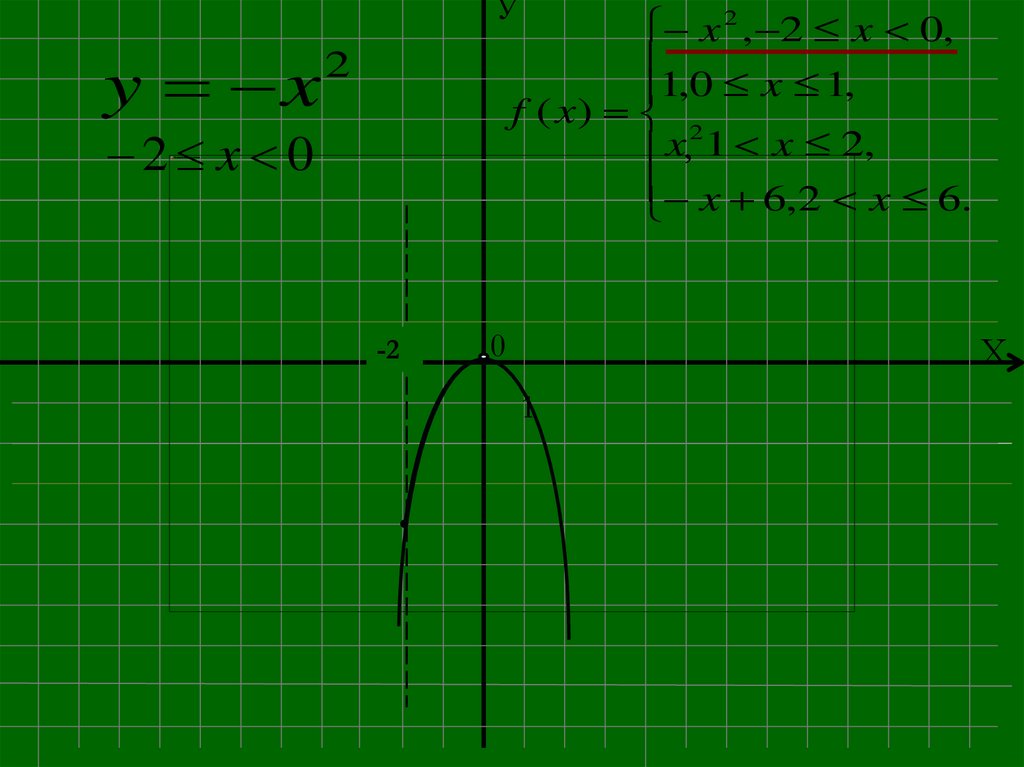
Построить график функции.x 2 , 2 x 0,
1,0 x 1,
f ( x) 2
x, 1 x 2,
x 6,2 x 6.
x = -2; 0; 1; 2; 6 - точки смены формул.
10.
Уy x
x 2 , 2 x 0,
1,0 x 1,
f ( x) 2
x, 1 x 2,
x 6,2 x 6.
2
2 x 0
-2
0
Х
1
11.
Уx 2 , 2 x 0,
1,0 x 1,
f ( x) 2
x , 1 x 2,
x 6,2 x 6.
y 1
0 x 1
1
Х
0
1
12.
Уy x
2
1 x 2
0
1 2
x 2 , 2 x 0,
1,0 x 1,
f ( x) 2
x , 1 x 2,
x 6,2 x 6.
Х
13.
Уy x 6
2 x 6
0
2
1
x 2 , 2 x 0,
1,0 x 1,
f ( x) 2
x,, 1 x 2,
x 6,2 x 6.
6
Х
14.
x 2 , 2 x 0, У1,0 x 1,
f ( x) 2
x , 1 x 2,
x 6,2 x 6.
-2
0 1
2
6
Х
15.
Построить график функцииx 5, x 1,
2
f ( x) 2( x 3) 2 ,1 x 4,
x 3 1,4 x 7.
X = 1; 4; 7 – точки смены формул.
16.
Уy=x+5
x 1
5
-5
0
1
Х
17.
Уy 2( x 3) 2 2
1 x 4
0
1
2
4
Х
18.
Уy x 3 1
x 3
4 x 7
0
1
3 4
7
Х
19.
x 5, x 1,f ( x) 2( x 3) 2 2 ,1 x 4,
x 3 1,4 x 7.
-5
У
5
0
1
3
7
Х
20. Свойства функции.
1. D(y)=(- ; 72. E(y)=(- ; 6
3. Промежутки возрастания
(- ; 1 2; 3
4. Промежутки убывания
1; 2 3; 4 4; 7
5. Наибольшее значение функции
Y=6
6. Функция непрерывная.



















 Математика
Математика








