Похожие презентации:
Простейшие функции и их графики
1.
Урок № 38Тема: Простейшие функции и их графики.
Задание:
1.Составить конспект на проверку присылать не
нужно.
Пройти тест: «Простейшие функции»
2.
3.
Функция вида y = kx +b, где k и bчисла, а x и y переменные,
называется линейной функцией.
x – независимая переменная (аргумент)
y – зависимая переменная (функция)
4.
Свойства линейной функции у = kx + в1. D (f) = (- ;+ )
у
у
2. E (f) = (- ;+ )
в
0
х
3. у = 0 при х = - в/к
в
4. Монотонность
0
k>0
возрастающая
х
k<0
убывающая
6. Нет ни наибольшего, ни наименьшего значений.
5. Не ограничена ни сверху, ни снизу.
7. Функция непрерывна.
Логинова Н.В. МБОУ «СОШ №16»
4
5.
Выбрав значение х (аргумента), можно легко вычислитьзначение y (функции)
у=2х+3
х = 0 у = 2 · х +3 = 0 +3 = 3
(0 ; 3)
х = 2 у = 2 · х +3 = 4+3 =7
(2 ;7)
6.
Совет:Если коэффициент k
положительный,
выбирай положительное
значение аргумента; если
отрицательный отрицательное
7.
Через две точки можно провеститолько одну прямую линию
Для построения графика линейной функции
достаточно двух точек!
8.
Коэффициентk
называют
угловым
коэффициентом.
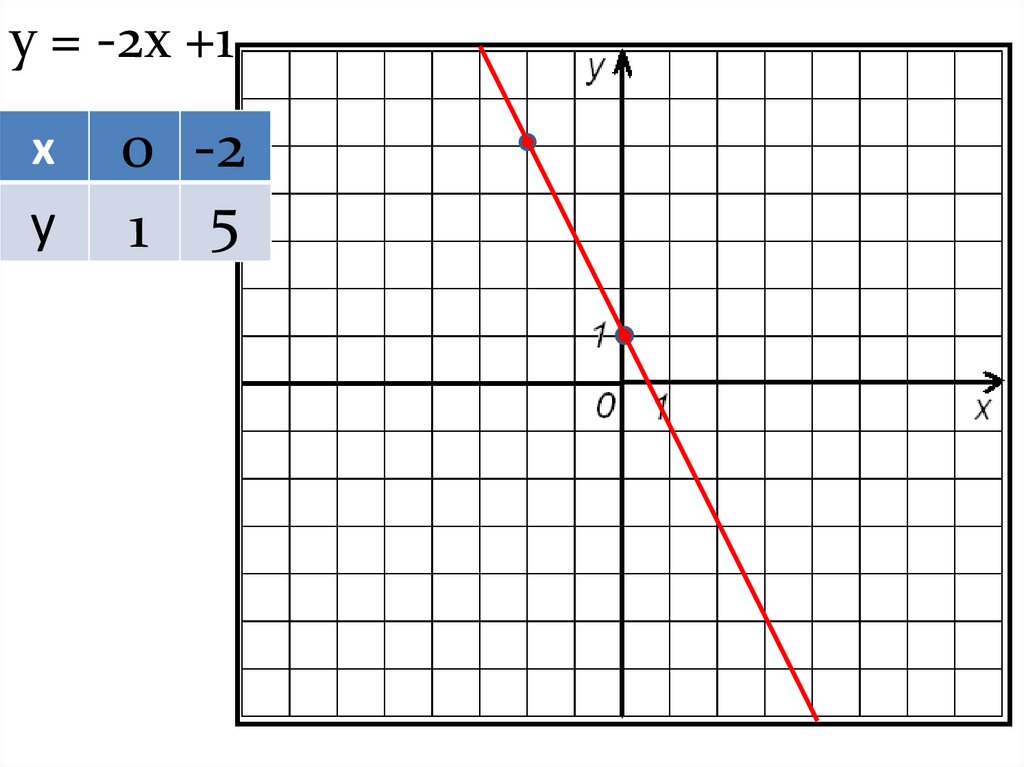
9.
у = -2х +1х
у
0 -2
1 5
10.
у = 2х - 50 3
у -5 1
х
11.
Чем больше угловойкоэффициент k, тем больше
угол, образованный графиком
функции с осью ОХ
12.
k = 0 - график параллелен оси ОХy
x
k=0
13.
Построим несколько графиковлинейных функций, у которых
одинаковые угловые коэффициенты.
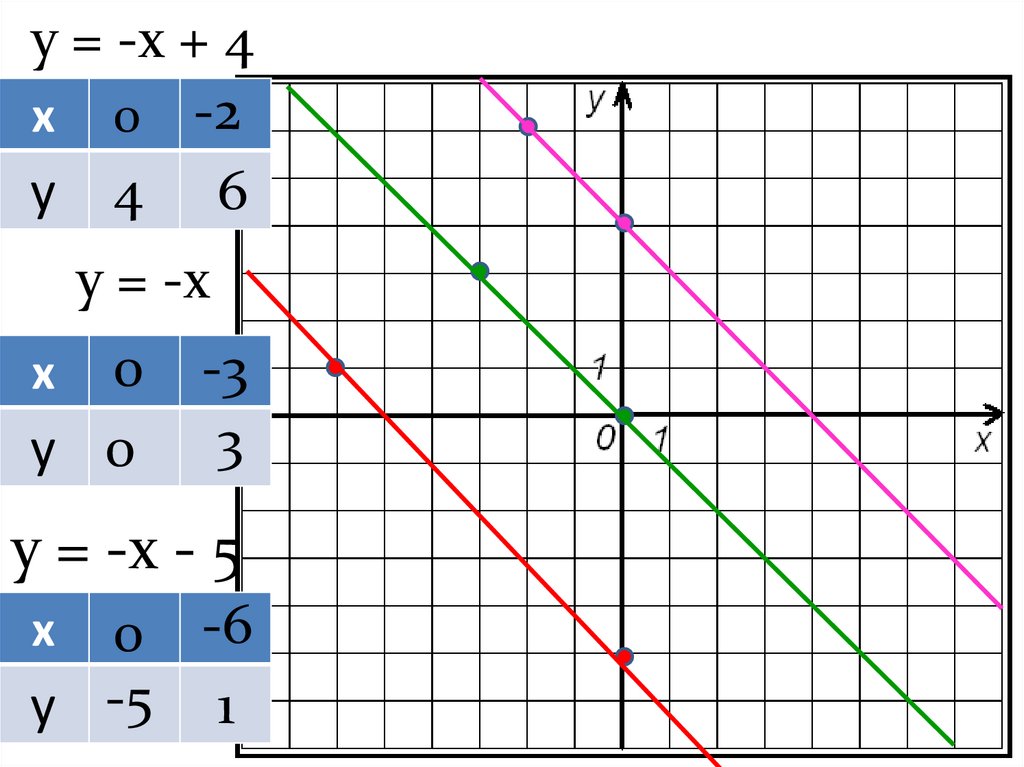
14.
у = -х + 4х 0 -2
у 4 6
у = -х
0
у 0
х
-3
3
у = -х - 5
0 -6
у -5 1
х
15.
Если у линейных функцийугловой коэффициент
одинаковый, то их графики
параллельны!
16.
Квадратичная функция и еесвойства.
17.
уу
0
х
Определение.
0
Функция вида у = ах2+bх+с,
где а, b, c – заданные числа, а≠0,
х – действительная переменная, называется
квадратичной функцией.
Примеры:
1) у=3х2-1
2) у=-2х2+х+3
3) у=4х2
4) у=-3х2+2х
х
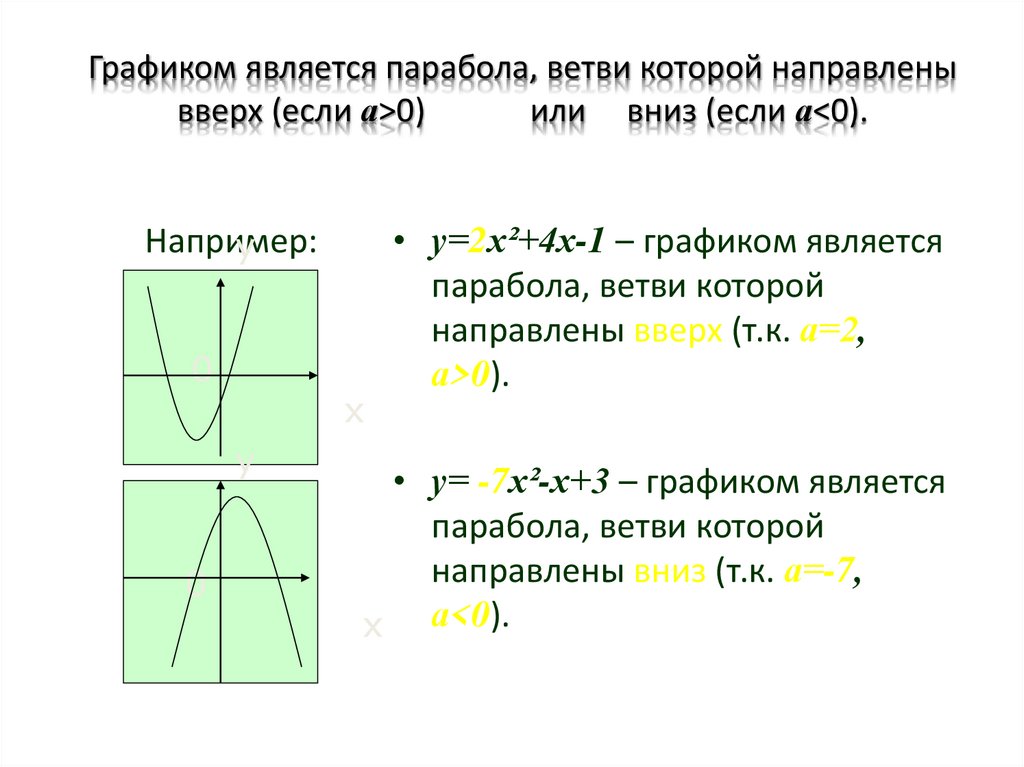
18.
Графиком является парабола, ветви которой направленывверх (если а>0)
или вниз (если а<0).
Например:
у
0
х
у
0
• у=2х²+4х-1 – графиком является
парабола, ветви которой
направлены вверх (т.к. а=2,
а>0).
• у= -7х²-х+3 – графиком является
парабола, ветви которой
направлены вниз (т.к. а=-7,
х а<0).
19.
Чтобы построить график функции надо:1. Описать функцию:
Пример: у = х²-2х-3 –
название функции,
что является графиком
функции,
куда направлены ветви
параболы.
квадратичная функция,
графиком является
парабола, ветви
которой направлены
вверх (т.к. а=1, а>0)
20.
Вершина параболы:Задание.
Найти координаты вершины параболы:
1) у = х 2 -4х-5
2) у=-5х 2+3
Ответ:(2;-9)
Ответ:(0;3)
Уравнение оси симметрии: х=m
х=2
х=0
21.
Свойства функции у = kx21. D (f) = (- ;+ )
y
k>0
y
k<0
0
x
2. Е (f) = [0;+ )
0
x
2. Е (f) = (- ;0]
3. у = 0 при х = 0
4.Промежутки монотонности
убывает на луче (- ;0], возрастает
на луче [0;+ )
убывает на луче [0;+ ),
возрастает на луче (- ;0]
5. унаим = 0; унаиб – не существует.
5. унаим – не существует; унаиб = 0.
6. Ограничена снизу.
6. Ограничена сверху.
7. Непрерывная, четная.
8. Выпукла вниз.
20.11.2020
8. Выпукла вверх.
Логинова Н.В. МБОУ «СОШ №16»
21
22.
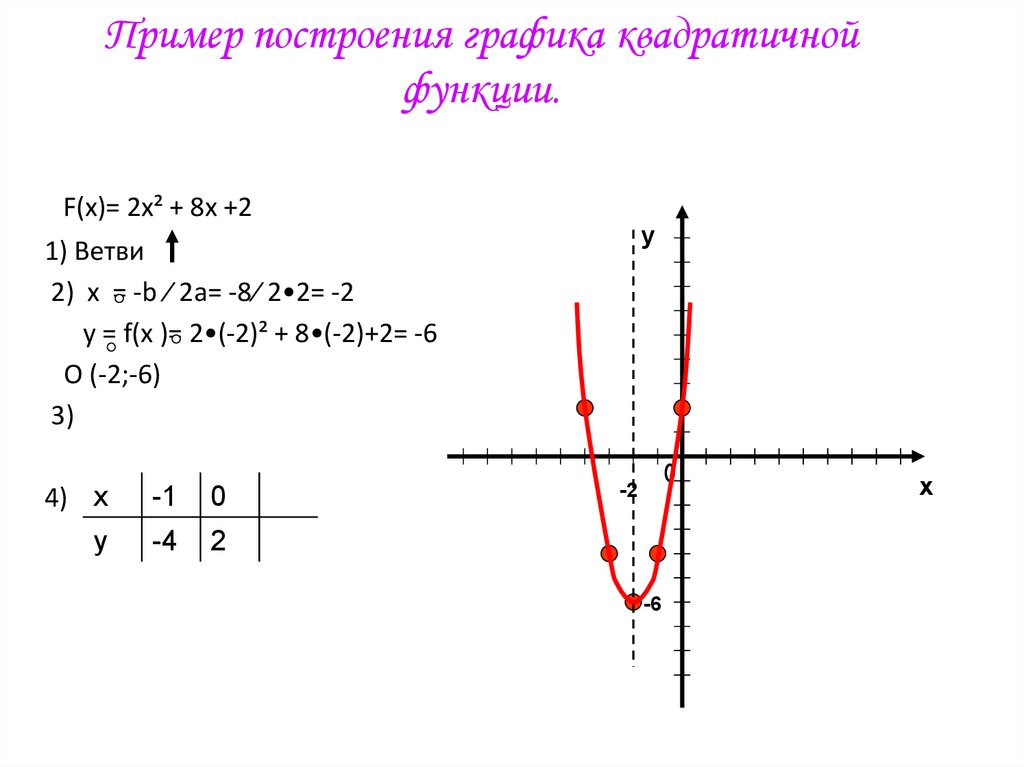
Пример построения графика квадратичнойфункции.
F(x)= 2x² + 8x +2
у
1) Ветви
2) х = -b ∕ 2a= -8∕ 2•2= -2
y = f(x )= 2•(-2)² + 8•(-2)+2= -6
O (-2;-6)
3)
4) х
-1
0
у
-4
2
х
-2
-6
23.
Обратная пропорциональность24.
Определение обратной пропорциональностиОбратной пропорциональностью называется
функция, которую можно задать формулой вида
k
у
x
где x — независимая переменная
у-зависимая переменная
k≠0
25.
Расположение графика функции«Обратная пропорциональность»
у
0 1
• Для k <0 график
х расположен
во II и IV
четверти
26.
Расположение графика функции«Обратная пропорциональность»
у
0
1
• Для k >0 график
расположен в
х
I и III четверти
27.
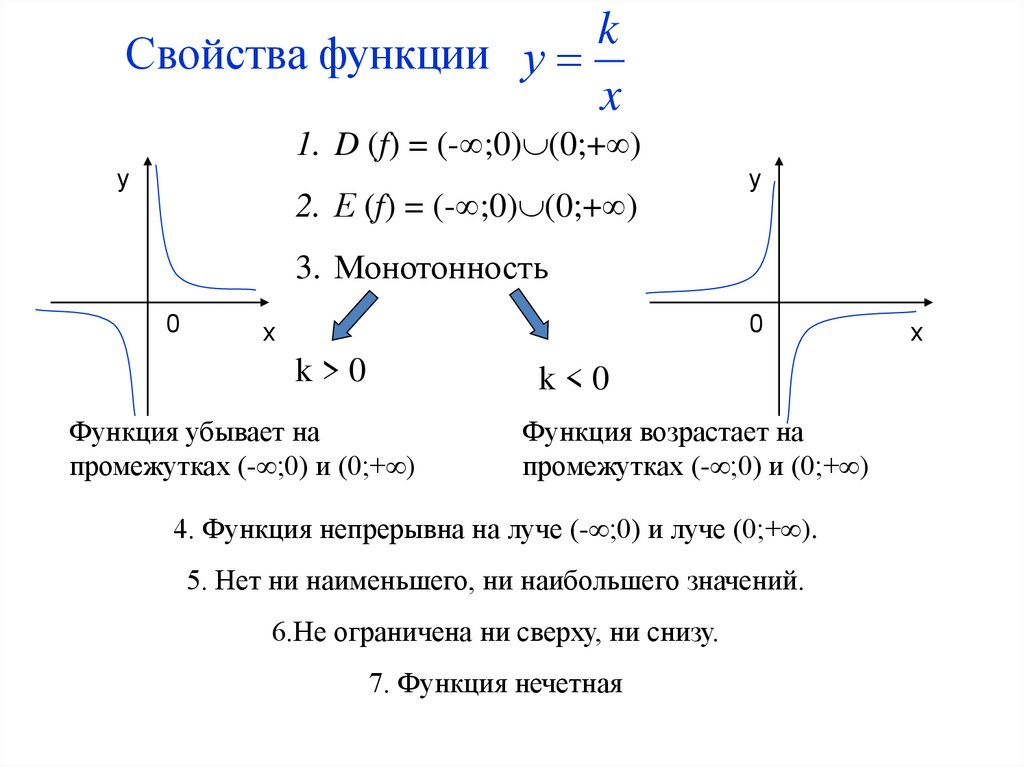
kСвойства функции у
x
1. D (f) = (- ;0) (0;+ )
у
2. Е (f) = (- ;0) (0;+ )
у
3. Монотонность
0
0
х
k>0
х
k<0
Функция убывает на
промежутках (- ;0) и (0;+ )
Функция возрастает на
промежутках (- ;0) и (0;+ )
4. Функция непрерывна на луче (- ;0) и луче (0;+ ).
5. Нет ни наименьшего, ни наибольшего значений.
6.Не ограничена ни сверху, ни снизу.
7. Функция нечетная
20.11.2020
27










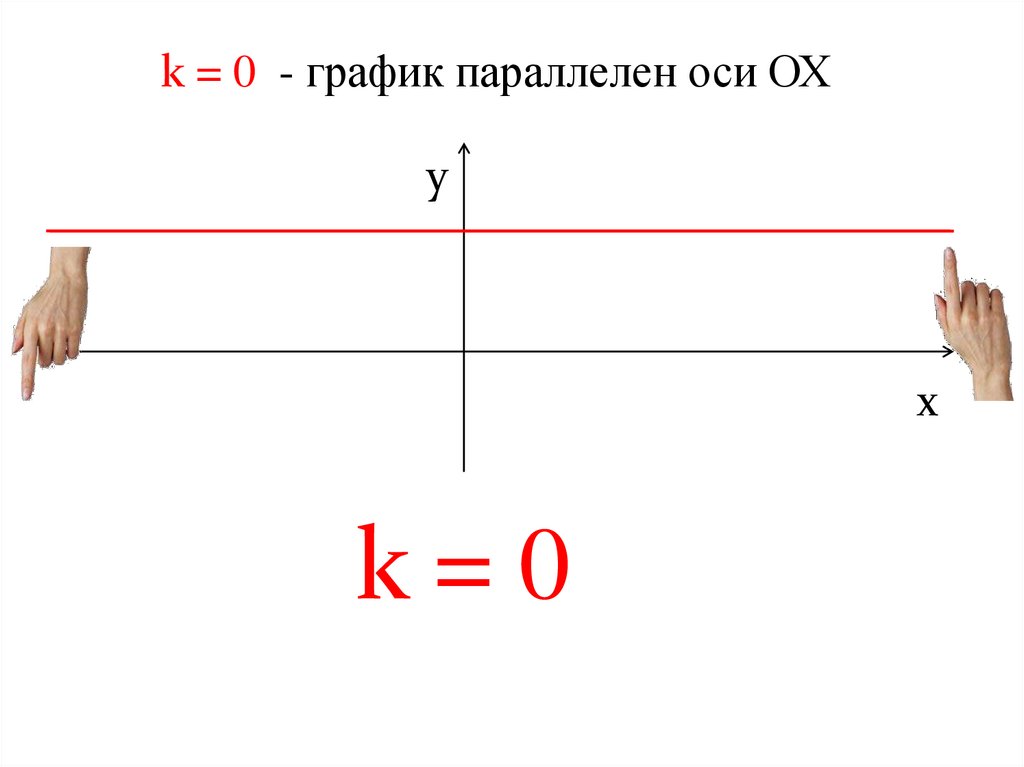











 Математика
Математика








