Треугольник. Первый признак равенства треугольника

1.

Треугольник. Первый
признак равенства
треугольника

2.

Цели урока:
а) познакомить учащихся с определением
треугольника и его элементов, формулировкой и
доказательством I признака равенства
треугольников;
б) развивать приемы логического мышления
(сравнивать, обобщать), правильно формулировать и
излагать мысли, умение анализировать факты и
делать выводы; создать условия для развития
познавательного интереса к математике;
в) воспитывать математическую культуру и речь.

3.

Эпиграф урока:
В старших классах каждый
школьник
Изучает треугольник.
Три каких-то уголка,
А работы — на века
(Валентин Берестов)

4.

Простейший из многоугольников –
треугольник – играет в геометрии
особую роль.
Без преувеличения можно сказать,
что вся (или почти вся) геометрия
со времён «Начал» Евклида
покоится на «трёх китах» - трёх
признаках равенства
треугольников.

5.

Для составления красивых паркетов часто использовали
треугольники .

6.

В

7.

Лишь на рубеже XIX – XX веков
математики научились строить
геометрию на основе более
фундаментального и общего,
чем равенство треугольников,
понятия геометрического
преобразования.
За несколько тысячелетий
геометры столь подробно
изучили треугольник, что
иногда говорят о
«геометрии треугольника»
как о самостоятельном разделе
элементарной геометрии.

8.

Треугольник
В
А
С

9.

Запомни!!!
Треугольник
– это геометрическая фигура,
состоящая из 3-х точек, не
лежащих на одной прямой, и
соединённых попарно
отрезками

10.

Элементы
треугольника
Треугольник АВС,
кратко: АВС или ВСА, САВ
Точки А,В,С – вершины
треугольника.
Отрезки АВ, ВС, СА – стороны
треугольника.
АВС, ВАС, АСВ или А, В, С–
углы треугольника
.

11.

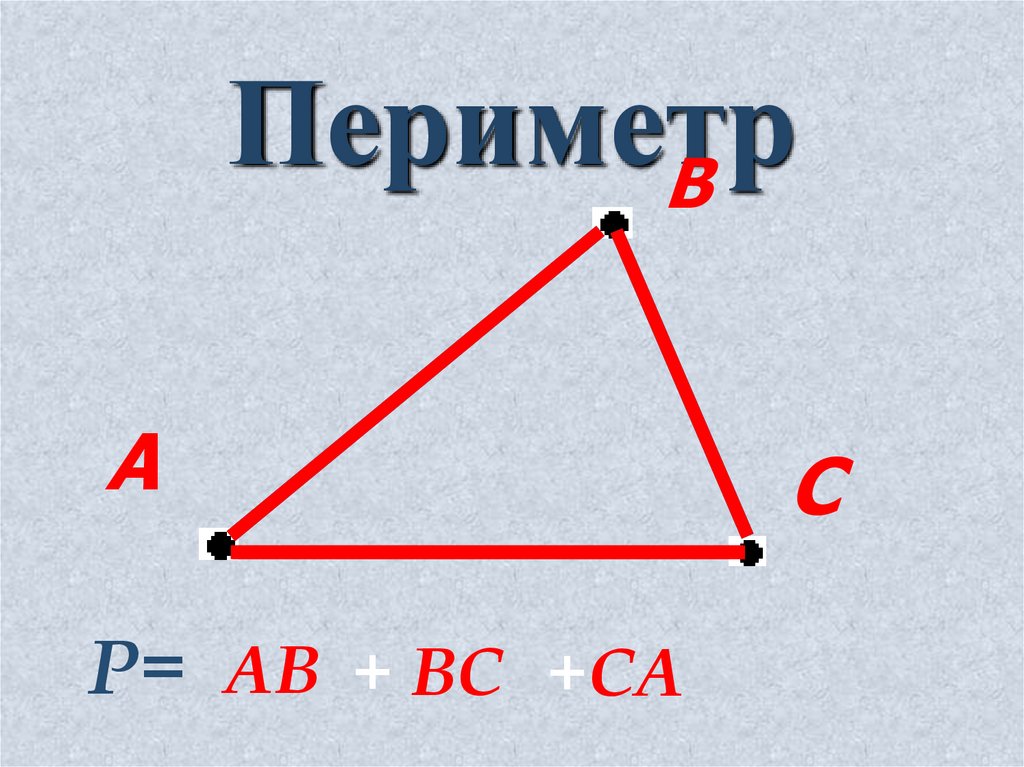
Периметр
В
А
Р= АВ + ВС +СА
С

12.

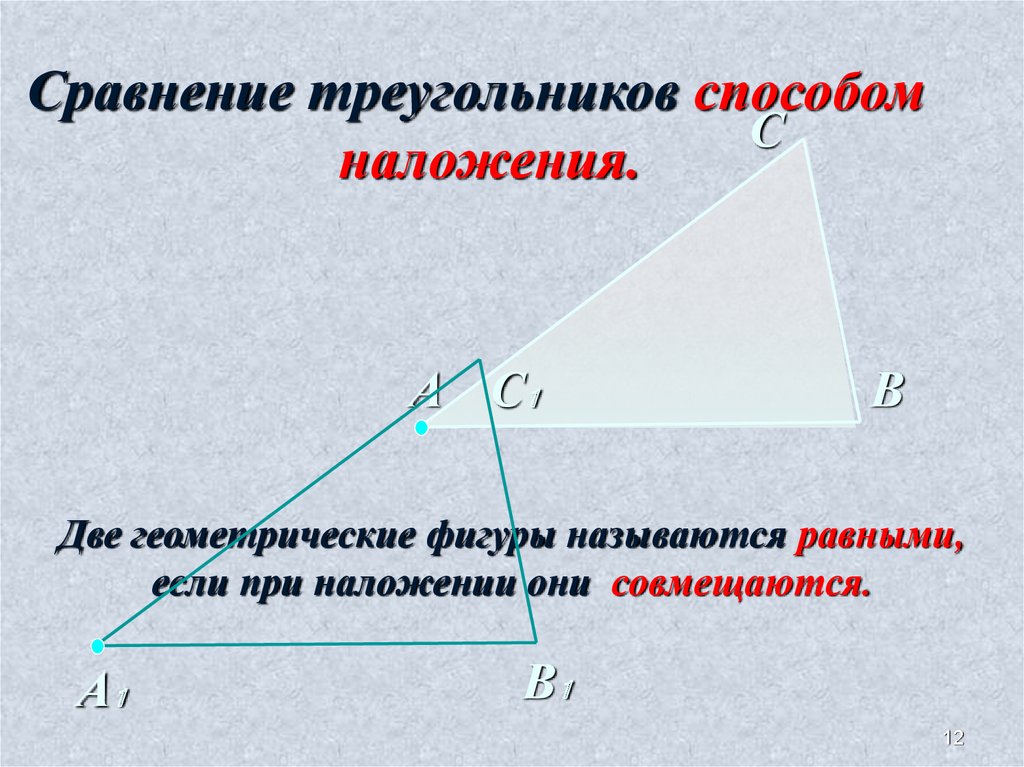
Сравнение треугольников способом
С
наложения.
А С₁
В
Две геометрические фигуры называются равными,
если при наложении они совмещаются.
А₁
В₁
12

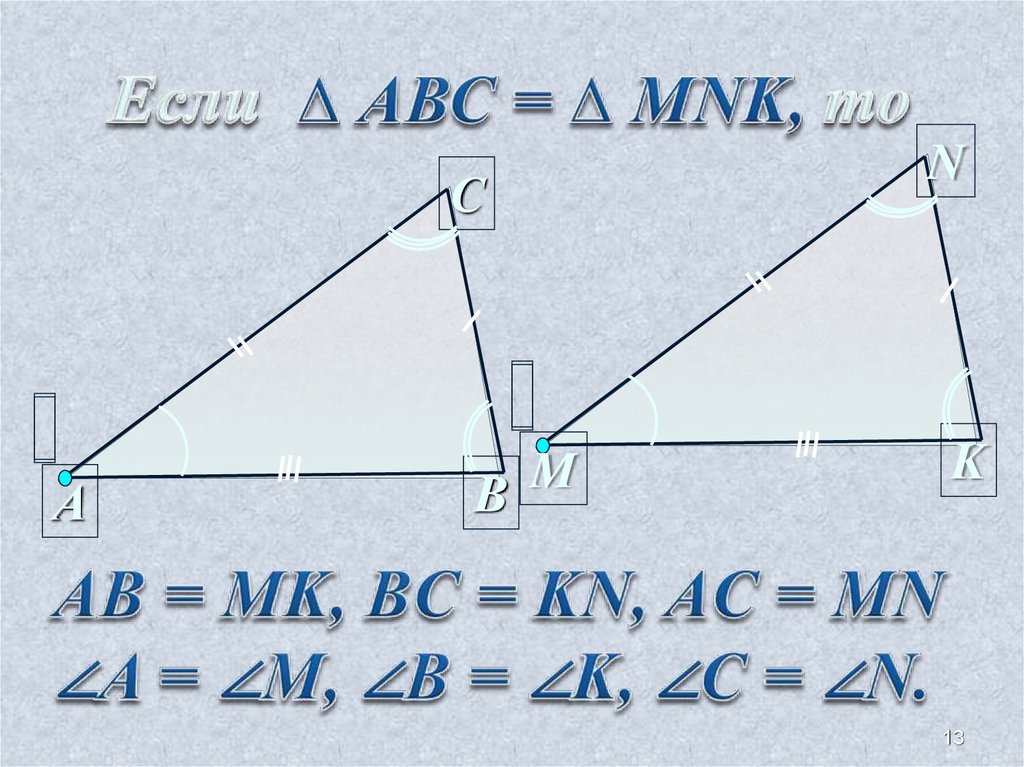
13.

С
А
M
В
N
K
13

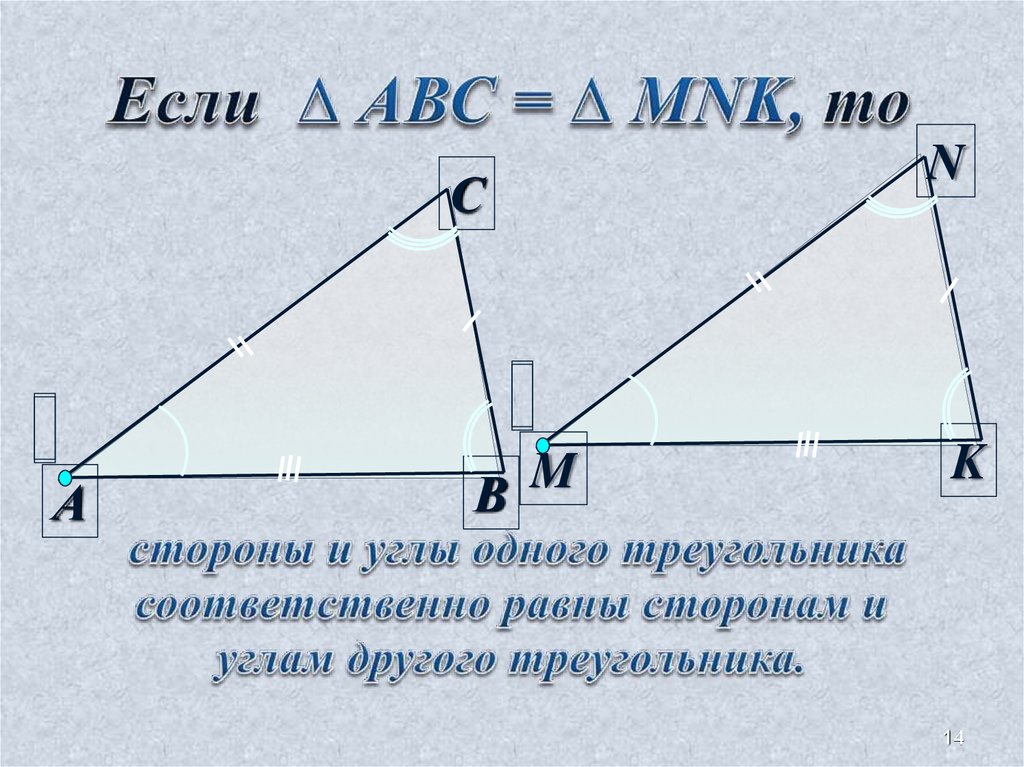
14.

С
А
M
В
N
K
14

15.

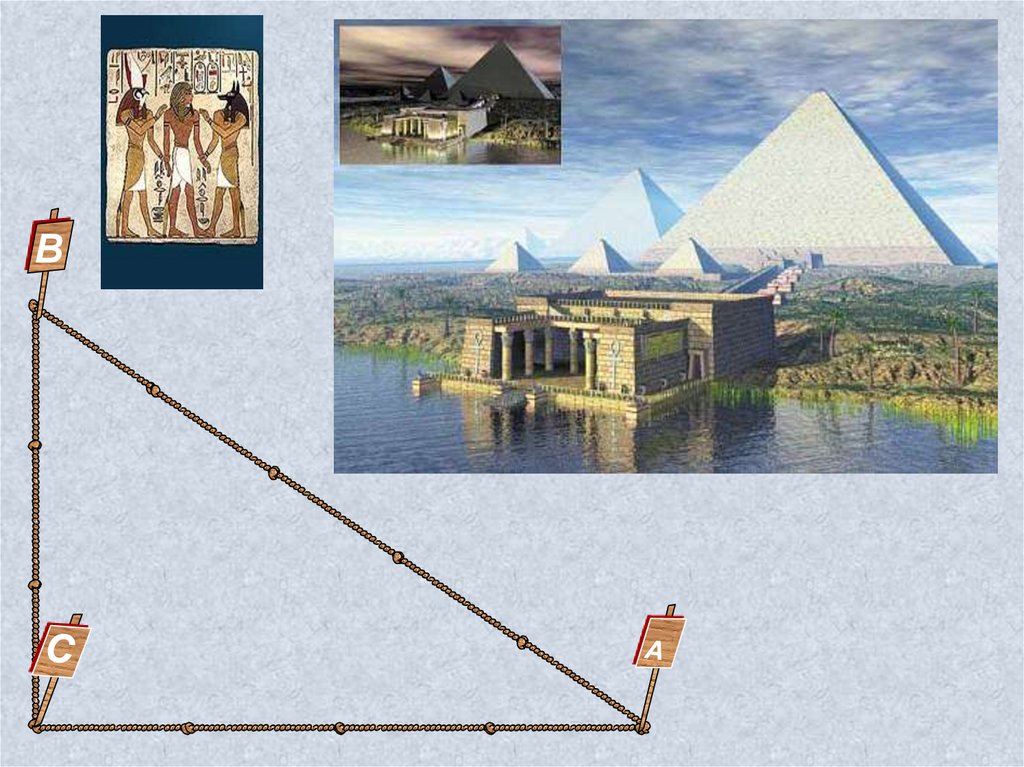
Исторический материал
Любой геометрический
материал возникает из
потребностей окружающей
жизни. Доказательство
признаков равенства
треугольников приписывают
древнегреческому ученому
Фалесу Милетскому (жившему
ок.625-547г.г. до н.э.). Теорему
о равенстве треугольников по
стороне и прилежащим к ней
двум углам он использовал для
определения расстояния от
берега до морских кораблей.

16.

ПЕРВЫЙ ПРИЗНАК
РАВЕНСТВА
ТРЕУГОЛЬНИКОВ
Если две стороны и угол между ними
одного треугольника равны
соответственно двум сторонам и
углу между ними другого
треугольника, то такие
треугольники равны.

17.

С
A
C1
B
A1
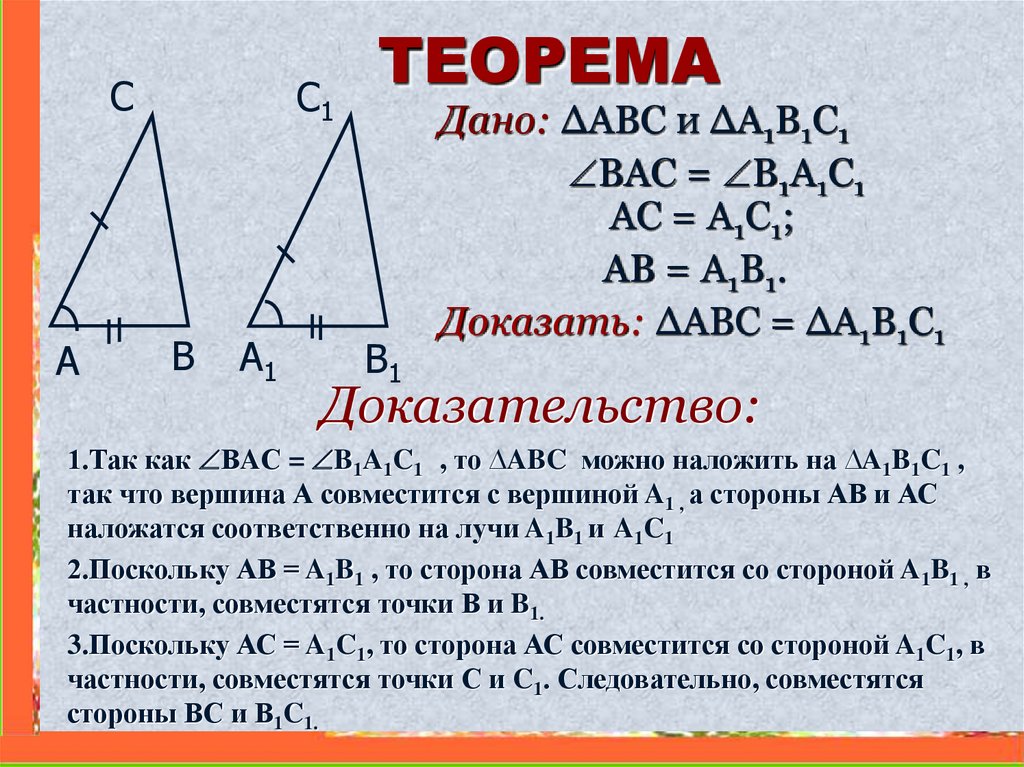
ТЕОРЕМА
B1
Дано: ∆ABC и ∆A1B1C1
ВAС = B1A1C1
AC = A1C1;
AB = A1B1.
Доказать: ∆ABC = ∆A1B1C1
Доказательство:
1.Так как ВAС = B1A1C1 , то ∆ABC можно наложить на ∆A1B1C1 ,
так что вершина А совместится с вершиной A1 , а стороны АВ и АС
наложатся соответственно на лучи A1B1 и A1C1
2.Поскольку АВ = A1B1 , то сторона АВ совместится со стороной A1B1 , в
частности, совместятся точки В и B1.
3.Поскольку АС = A1C1, то сторона АС совместится со стороной A1C1, в
частности, совместятся точки С и C1. Следовательно, совместятся
стороны ВС и В1C1.

18.

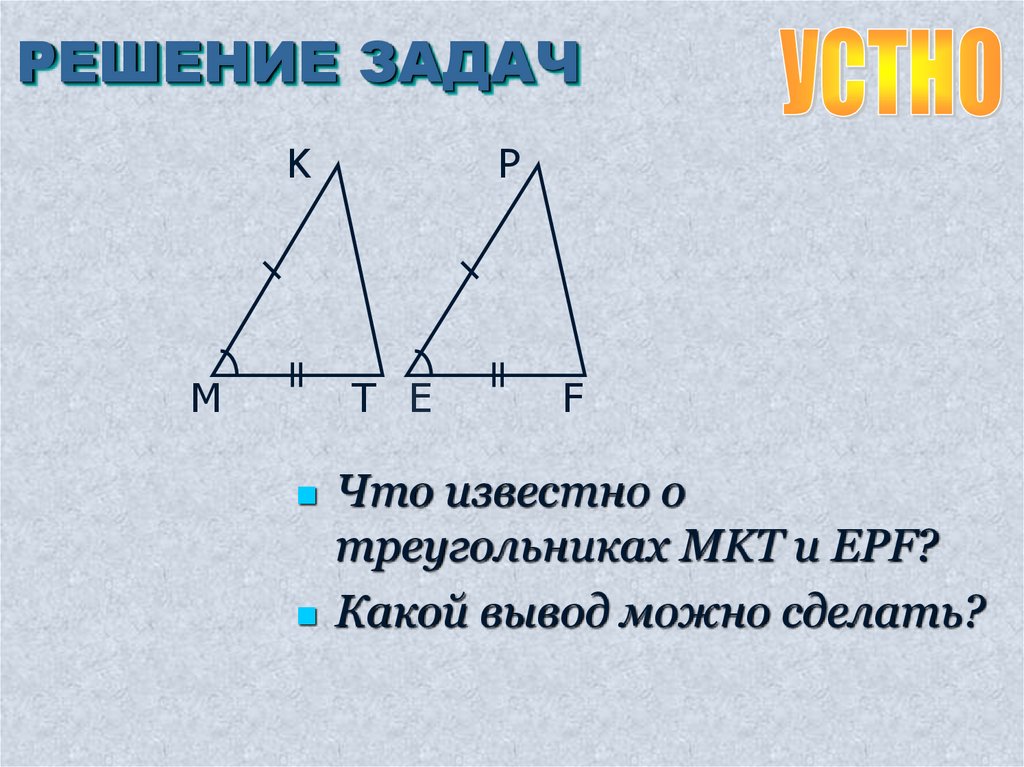
РЕШЕНИЕ ЗАДАЧ
K
M
P
T E
F
Что известно о
треугольниках MKT и EPF?
Какой вывод можно сделать?

19.

РЕШЕНИЕ ЗАДАЧ
B
D
O
A
C
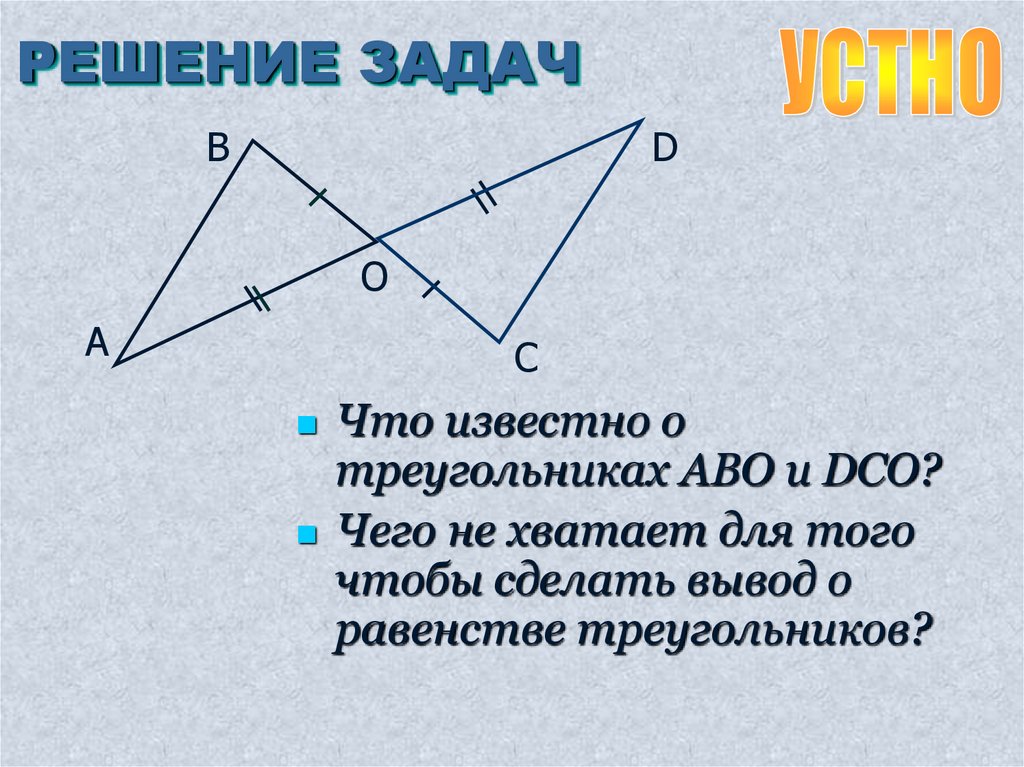
Что известно о
треугольниках ABO и DCO?
Чего не хватает для того
чтобы сделать вывод о
равенстве треугольников?

20.

ЗАДАЧА №3
A
1
2
(№94а)
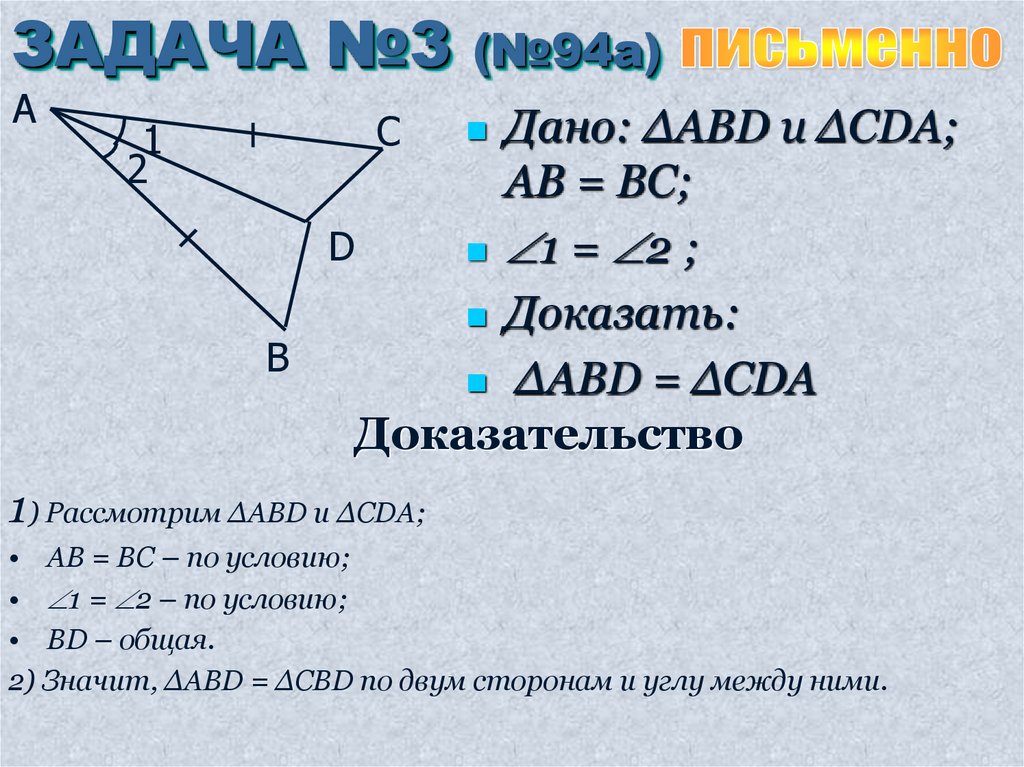
Дано: ∆ABD u ∆CDA;
AB = BC;
D
1 = 2 ;
Доказать:
B
∆ABD = ∆CDA
Доказательство
C
1) Рассмотрим ∆ABD и ∆CDA;
• AB = BC – по условию;
• 1 = 2 – по условию;
• BD – общая.
2) Значит, ∆ABD = ∆CBD по двум сторонам и углу между ними.

21.

ЗАДАЧА №4
B
1
C
(№95a)
2
A
D
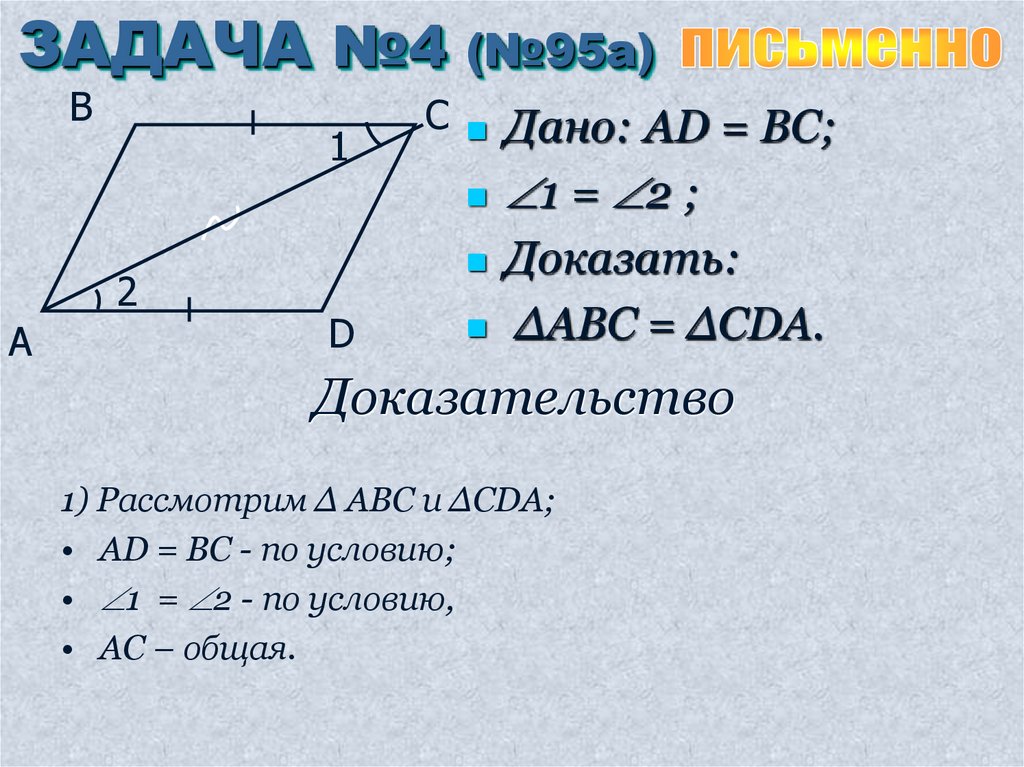
Дано: AD = BC;
1 = 2 ;
Доказать:
∆ABC = ∆CDA.
Доказательство
1) Рассмотрим ∆ ABC и ∆CDA;
• AD = BC - по условию;
• 1 = 2 - по условию,
• AC – общая.

22.

СОСЧИТАЙ
ТРЕУГОЛЬНИКИ

23.

ДОМАШНЕЕ ЗАДАНИЕ
Пункт 14,15. Теорему и
доказательство
записать в тетрадь и
учить;
№96, 98

24.

Спасибо за
урок !