Расчет поля тонкого заряженного провода над землей; двухпроводной линии над землей; рабочая емкость с учетом влияния земли

1.

Краткое содержание
1. Методы изображений
2. Расчет поля тонкого заряженного провода
над землей; двухпроводной линии над
землей; рабочая емкость с учетом влияния
земли
3. Потенциальные коэффициенты,
коэффициенты электростатической
индукции; емкостные коэффициенты
4. Задача Сирла

2.

Теорема существования:
Решение уравнений поля, которое удовлетворяет
граничным условиям, является единственным.
В однородной среде при одинаковой геометрической форме
электродов и разности потенциалов между ними распределение
потенциала всегда одинаково. Любое решение,
удовлетворяющее уравнениям поля и граничным условиям
можно считать полным и единственным в той части
пространства, где поле есть.
Следствия:
1) Электростатическое поле, ограниченное эквипотенциальными
поверхностями и решение для характеристик поля не изменится, если
эти поверхности рассматривать как поверхности проводников
(электроды), которым сообщены соответствующие потенциалы. Этим
приемом пользуются при расчете полей параллельных круглых
проводов.
2) Электростатическое поле по одну сторону от плоской поверхности S
границы раздела сред и решение, описывающее поле, не изменится,
если по другую сторону от этой поверхности изменить параметры среды
и распределение зарядов так, чтобы сохранились граничные условия
на поверхности S. На этом основан метод зеркальных
изображений.
2

3.

d 2a
r0
( (0) 0)
В декартовой системе координат
a x
r (a x) 2 y 2
y
M ( x, y )
a x
вне проводов
( x, y ) E iEx jE y
Ex ( x, y )
горизонтальная
E y ( x, y )
вертикальная
r (a x) 2 y 2
0U
подставим C0U
2a
ln
r0
( x, y ) E ( x, y ) ( x, y )
y
E x ( x, y )
y
x
(a x) 2 y 2
r
( x, y )
ln
ln
2 0 r
2 0
(a x) 2 y 2
(a x)2 y 2
U
( x, y )
ln
2
2
2a
(
a
x
)
y
2ln
r0

4.

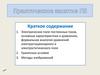
2a
E
E
M
r r
E
r0
( x a)2 y 2
r
k
2
2
r
( x a) y
Эквипотенциали в
плоскости X0Y
концентрические
окружности
a
a
Поверхность нулевого (равного) потенциала – плоская поверхность,
расположенная между проводами; для плоскопараллельного поля – прямая,
расположенная ровно посередине между тонкими заряженными проводами,
если С=0, то совпадающая с осью OY . Для т. М (0,y) r r E E
E E E
E const

5.

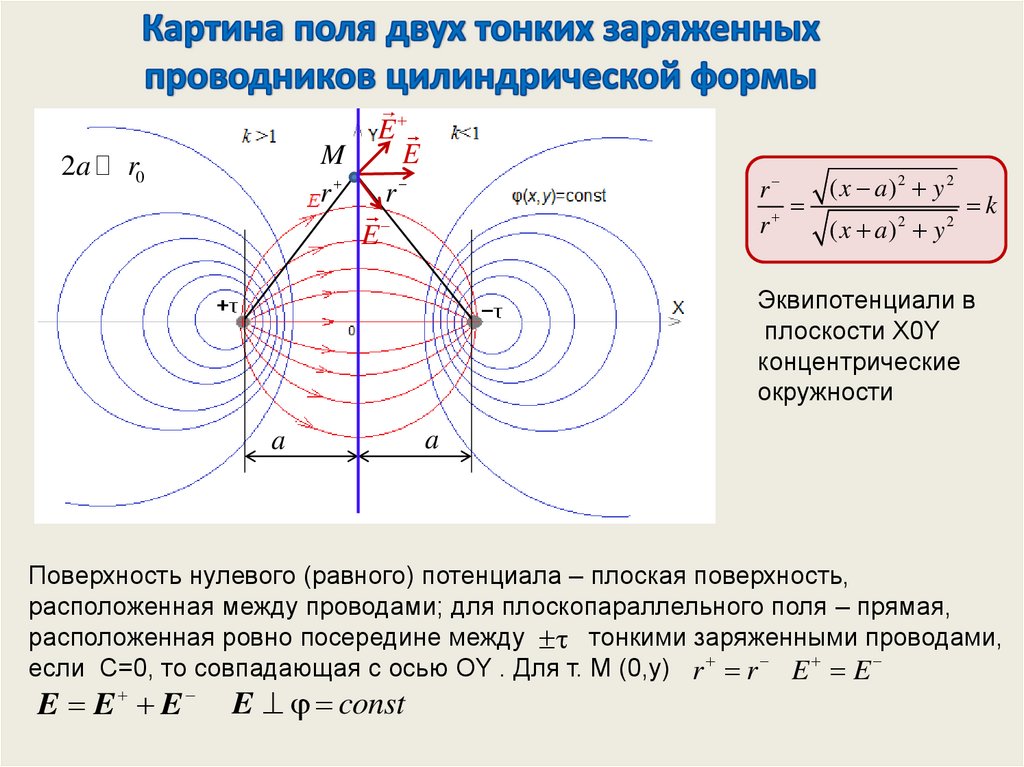
На границе раздела диэлектрик-проводник
qсв св ds
D2 n D1n св
S
св - поверхностная плотность свободного
заряда
[ Кл/м2 ]
Dn r 0 En 0 En 0
n
1
2
составляющая вектора электрического
смещения, нормальная к поверхности
E1n E y ( x,0)
( x, y )
y
0
D2 n D1n св
y 0
св ( x) D1n 0 E1n 0
n
( x, y )
y
y 0
5

6.

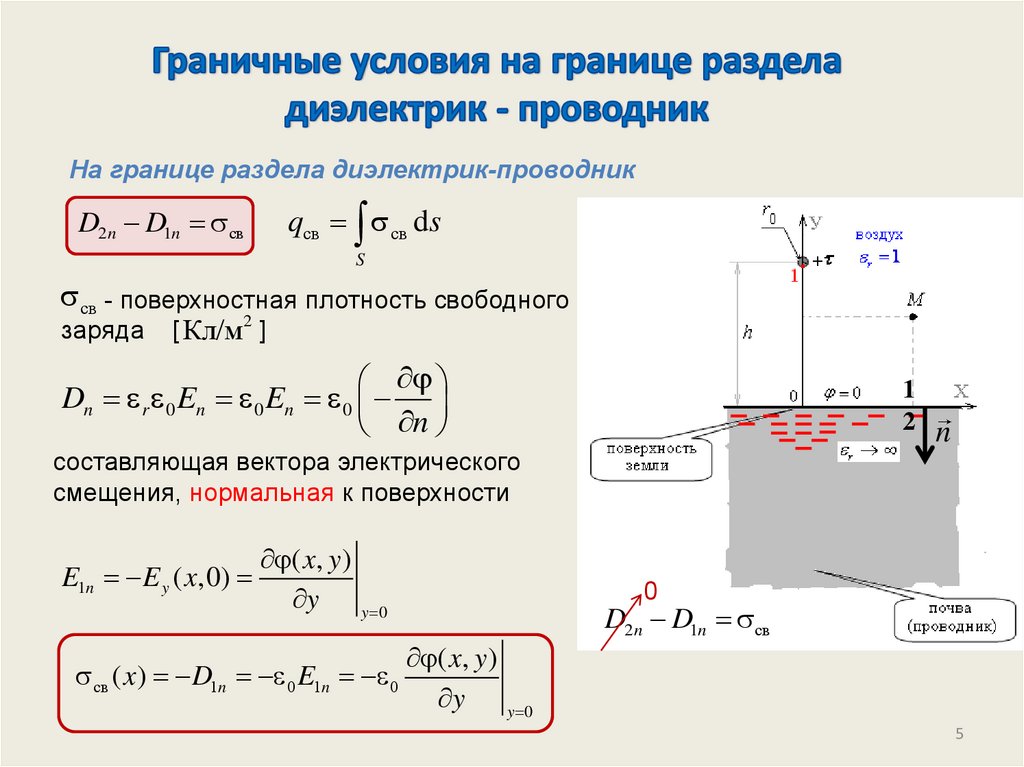
Расположим провода вертикально
2a
r0
0
a
0 const
0
0 const
E const
E
E
a
r
меняем параметры среды:
полностью заполняем область y<0
проводящей средой
граничные условия не меняются

7.

h
r0
E 0
2h
r0
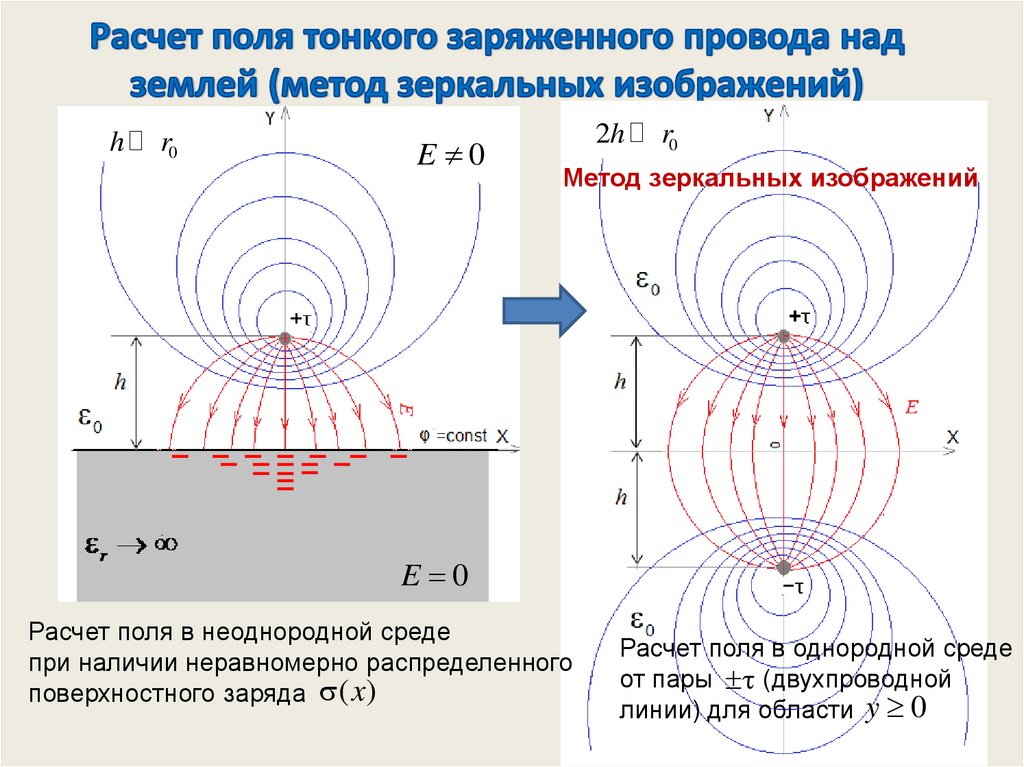
Метод зеркальных изображений
E 0
Расчет поля в неоднородной среде
при наличии неравномерно распределенного
поверхностного заряда ( x)
Расчет поля в однородной среде
от пары (двухпроводной
линии) для области y 0

8.

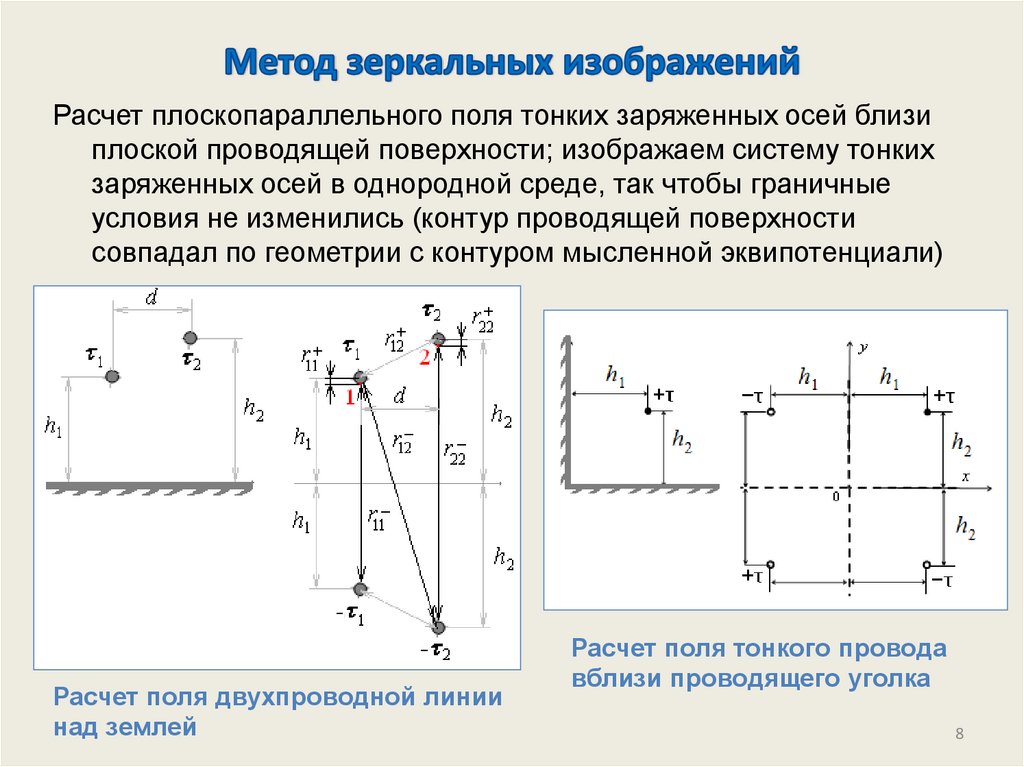
Расчет плоскопараллельного поля тонких заряженных осей близи
плоской проводящей поверхности; изображаем систему тонких
заряженных осей в однородной среде, так чтобы граничные
условия не изменились (контур проводящей поверхности
совпадал по геометрии с контуром мысленной эквипотенциали)
Расчет поля двухпроводной линии
над землей
Расчет поля тонкого провода
вблизи проводящего уголка
8

9.

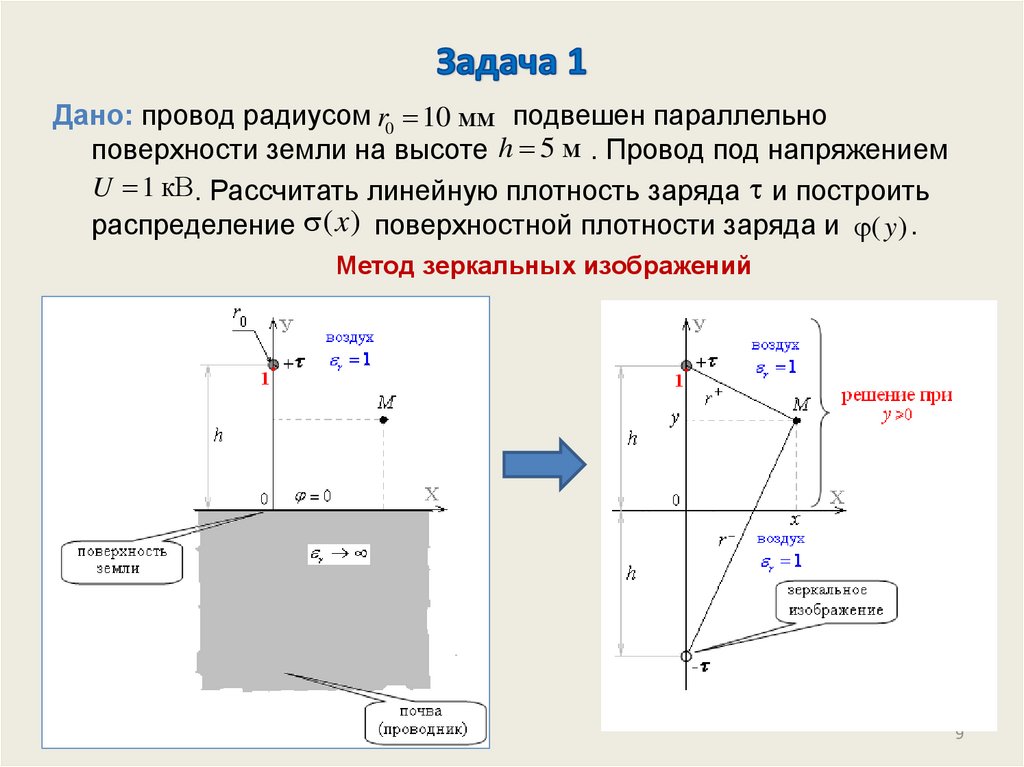
Дано: провод радиусом r0 10 мм подвешен параллельно
поверхности земли на высоте h 5 м . Провод под напряжением
U 1 кВ. Рассчитать линейную плотность заряда и построить
распределение ( x) поверхностной плотности заряда и ( y ) .
Метод зеркальных изображений
9

10.

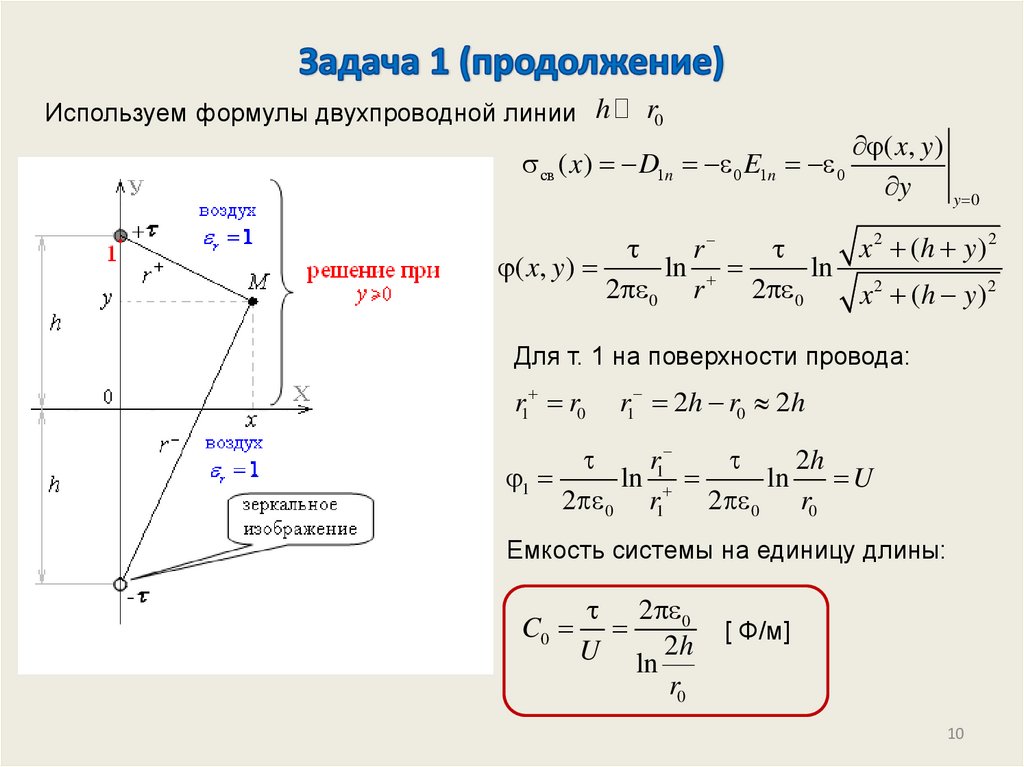
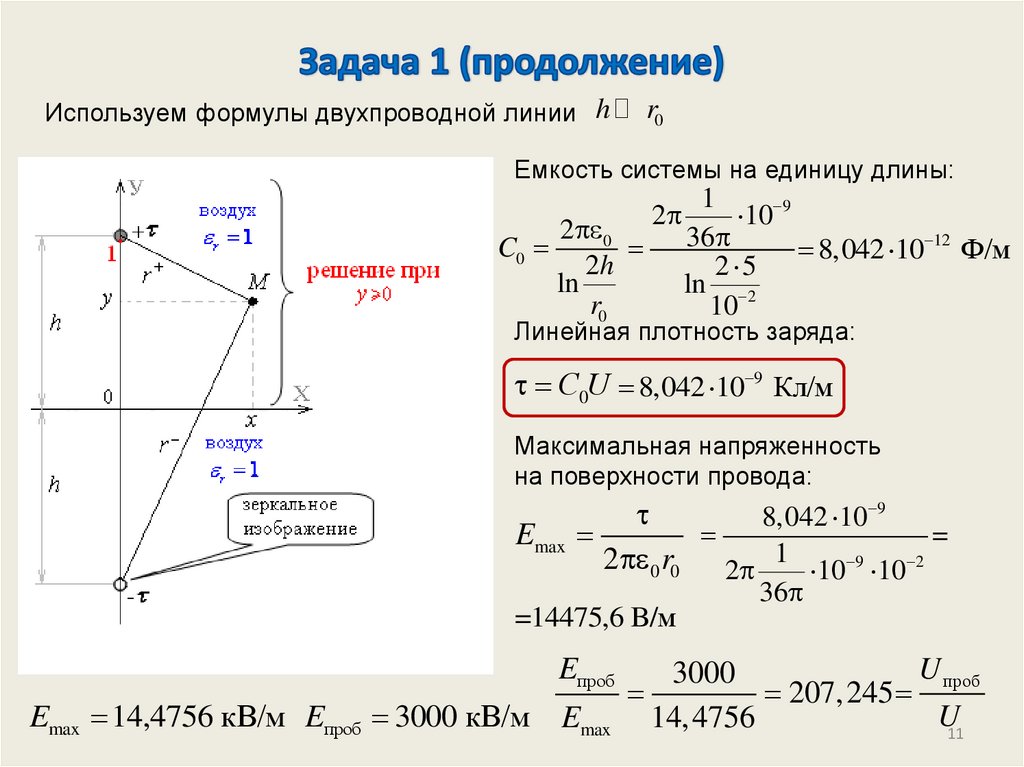
Используем формулы двухпроводной линии h
r0
св ( x) D1n 0 E1n 0
( x, y )
y
y 0
x 2 (h y ) 2
r
( x, y )
ln
ln
2 0 r
2 0
x 2 (h y ) 2
Для т. 1 на поверхности провода:
r1 r0
r1 2h r0 2h
r1
2h
1
ln
ln
U
2 0 r1
2 0 r0
Емкость системы на единицу длины:
C0
2 0
U ln 2h
r0
[ Ф/м]
10

11.

Используем формулы двухпроводной линии h
r0
Емкость системы на единицу длины:
C0
2 0
2h
ln
r0
2
1
10 9
36
8,042 10 12 Ф/м
2 5
ln 2
10
Линейная плотность заряда:
С0U 8,042 10 9 Кл/м
Максимальная напряженность
на поверхности провода:
Emax
8,042 10 9
=
1
2 0 r0 2
10 9 10 2
=14475,6 B/м
Eпроб
Emax 14,4756 кB/м Eпроб 3000 кB/м Emax
36
U проб
3000
207,245
U11
14,4756

12.

Используем формулы двухпроводной линии h
Для потенциала: ( x, y ) y 0
r0
x 2 (h y ) 2
ln
2 0
x 2 (h y ) 2
Вертикальная составляющая напряженности эл. поля:
E y ( x, y )
1 2(h y )
2(h y )( 1)
( x, y )
2
2
2
2
2 0 2 x (h y )
x (h y )
y
(h y )
(h y )
2
2 0 x (h y ) 2 x 2 (h y ) 2
( x, y )
E1n E y ( x,0)
y
y 0
h
h
h
2
2
2
2
2
2 0 x h
x h 0 x h 2
h
св ( x) 0 E1n 2
x h 2
свmax св (0)
h
12

13.

Другое решение задачи
Напряженность поля :
E y E y E y
модули E
E
2 0 r
2 0 r
на поверхности земли
2
2
y 0, x r r h x
для проекций на ось OY
E y E y E sin
E y ( x) E y E y 2
h
2 0 h 2 x 2
h2 x 2
2 0 h 2 x 2
h
h2 x2
h
0 (h 2 x 2 )
Распределение поверхностной плотности заряда: св ( x) 0 E y
h
(h 2 x 2 )
13

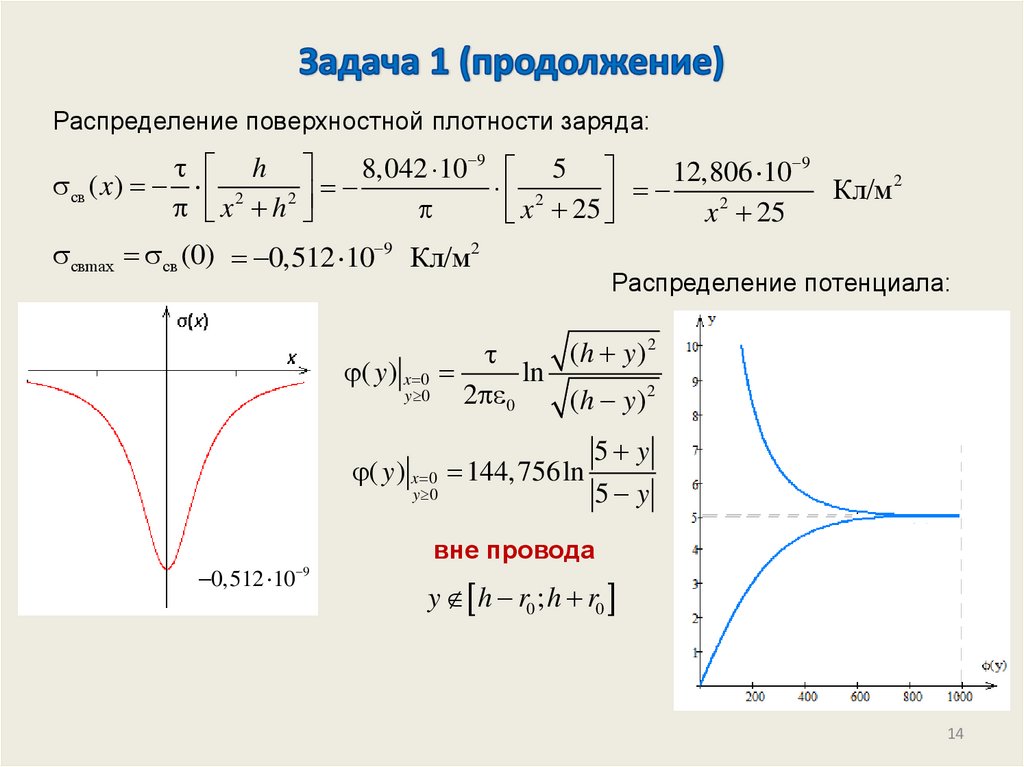
14.

Распределение поверхностной плотности заряда:
9
h
8,042 10 9 5
12,806
10
2
св ( x) 2
Кл/м
x 2 25
x h 2
x 2 25
свmax св (0) 0,512 10 9 Кл/м2
( y ) x 0
(h y ) 2
ln
2 0
(h y ) 2
( y ) x 0
5 y
144,756ln
5 y
y 0
y 0
0,512 10
9
Распределение потенциала:
вне провода
y h r0 ; h r0
14

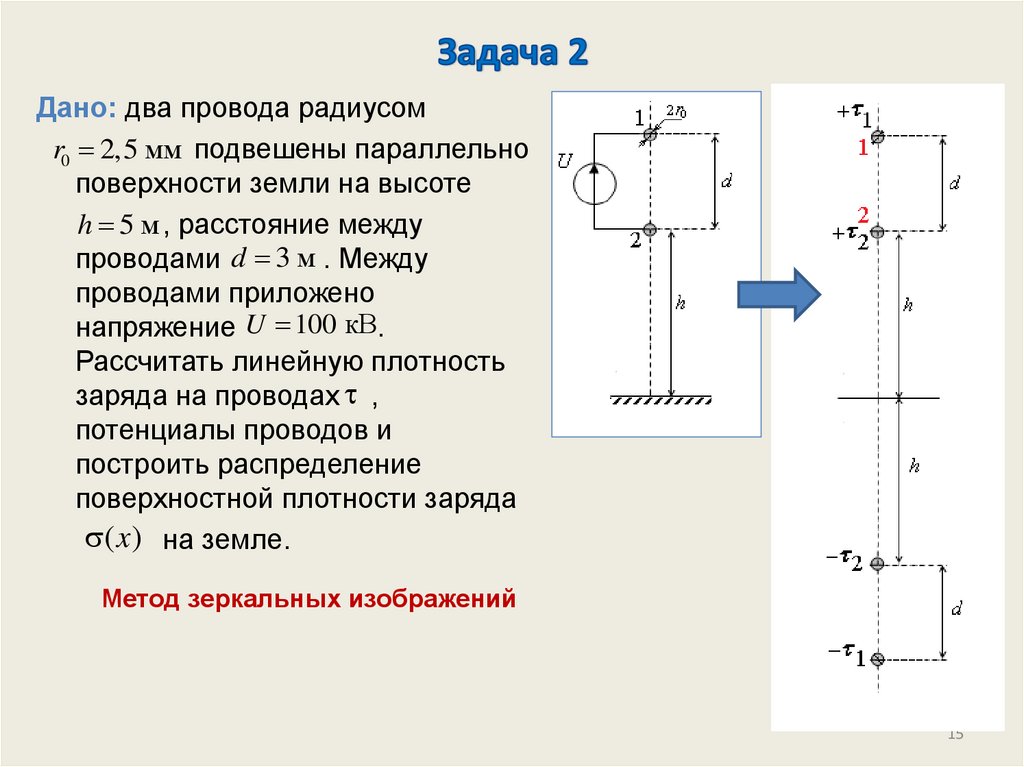
15.

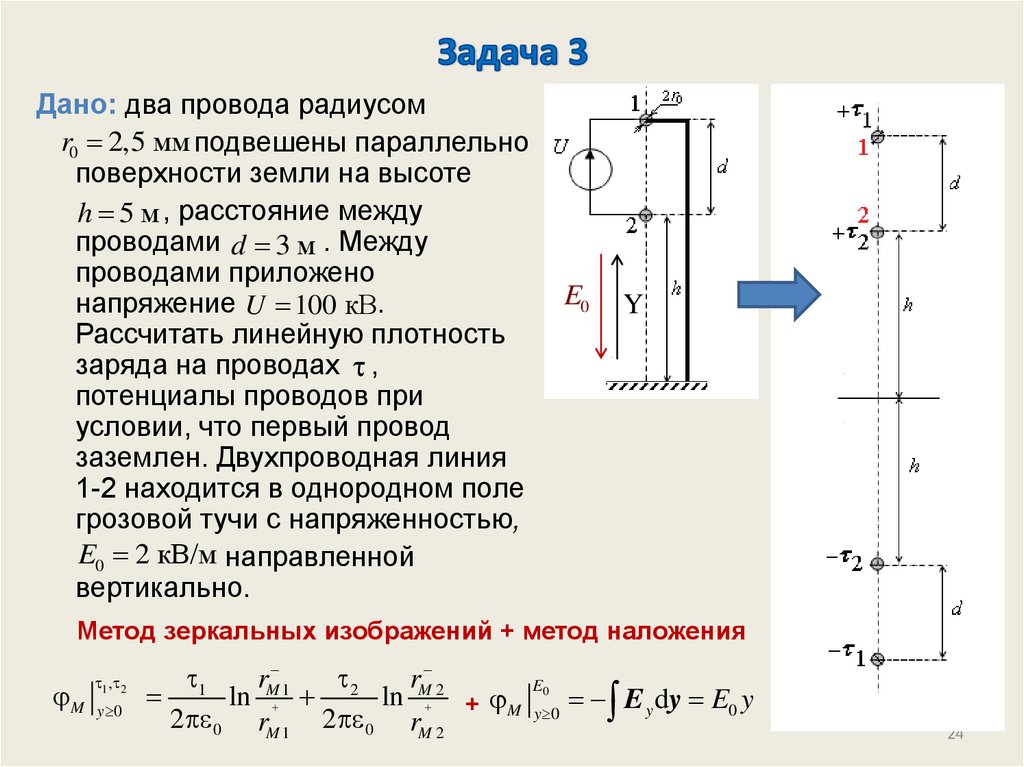
Дано: два провода радиусом
r0 2,5 мм подвешены параллельно
поверхности земли на высоте
h 5 м , расстояние между
проводами d 3 м . Между
проводами приложено
напряжение U 100 кВ.
Рассчитать линейную плотность
заряда на проводах ,
потенциалы проводов и
построить распределение
поверхностной плотности заряда
( x) на земле.
Метод зеркальных изображений
15

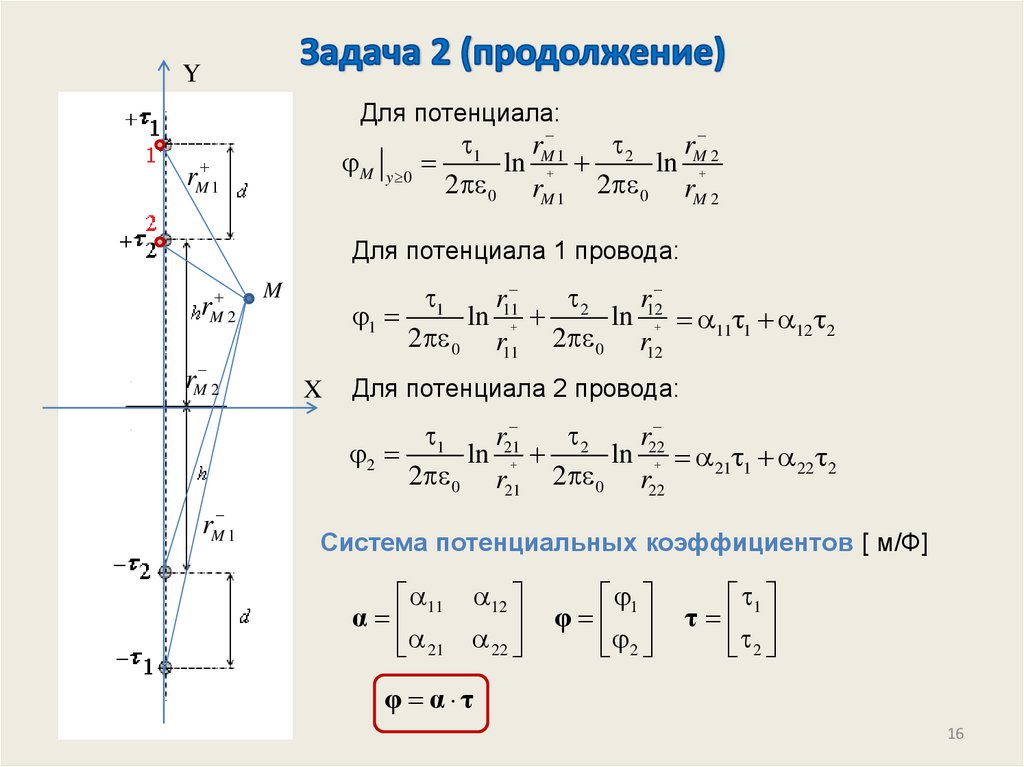
16.

Y
Для потенциала:
M
rM 1
y 0
1
rM 1
2
rM 2
ln
ln
2 0 rM 1 2 0 rM 2
Для потенциала 1 провода:
M2
r
rM 2
1
r11
2
r12
1
ln
ln 11 1 12 2
2 0 r11 2 0 r12
M
X
Для потенциала 2 провода:
1
r21
2
r22
2
ln
ln 21 1 22 2
2 0 r21 2 0 r22
rM 1
Система потенциальных коэффициентов [ м/Ф]
12
α 11
22
21
φ 1
2
τ 1
2
φ α τ
16

17.

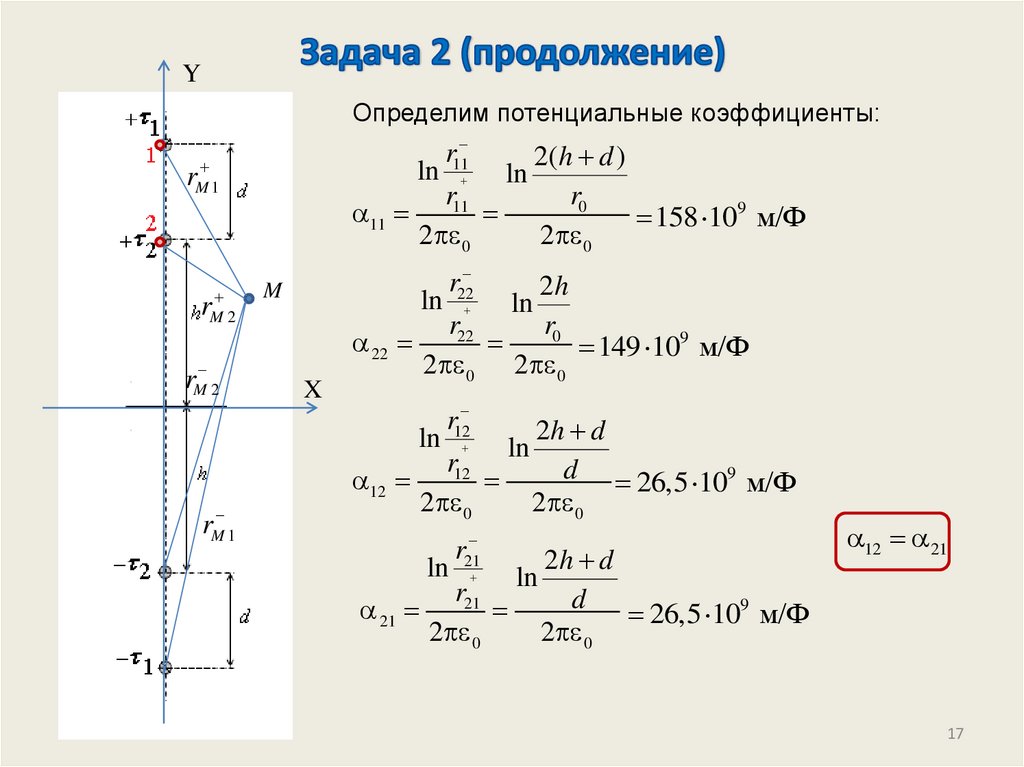
Y
Определим потенциальные коэффициенты:
r11
2( h d )
ln ln
r0
r11
11
158 109 м/Ф
2 0
2 0
rM 1
rM 2
rM 2
rM 1
M
X
r22
2h
ln ln
r0
r22
22
149 109 м/Ф
2 0 2 0
r12
ln ln 2h d
r12
d 26,5 109 м/Ф
12
2 0
2 0
r21
ln ln 2h d
r21
d
21
26,5 109 м/Ф
2 0
2 0
12 21
17

18.

Потенциальные коэффициенты:
158 109
α
9
26,5
10
26,5 109
149 109
[ м/Ф]
С учетом граничных условий:
1 11 1 12 2
2 21 1 22 2
1 11 12
2 21 22
U 1 2 11 12 21 22
Рабочая емкость на единицу длины:
Изолированная система:
1 0
τ
1
2
2
1
2
1 U
φ
1
2
2
1
C0 C раб
U 11 22 2 12
1
12
3,937
10
Ф/м
9
158 149 2 26,5 10
C раб
C раб
Емкость на единицу длины без учета земли:
C0
0
0
3,918 10 12 Ф/м
d
3
ln
ln
r0
2,5 10 3
18

19.

Линейная плотность зарядов:
C рабU 393,7 10 9 Кл/м
1 393,7 10 9 Кл/м 2 393,7 10 9 Кл/м
Потенциалы проводов:
1 11 12 158 26,5 109 393,7 10 9 51771,55 B
9
2 21 22 26,5 149 109 393,7 10
48228,25 B
Проверка: U 1 2 99999,8 B 100 кВ
Система коэффициентов электростатической индукции
Изолированная система:
1 0
τ
1
2
2
1
2
1 U
φ
1
2
2
12
1
β 11
φ
22
21
2
τ β φ
τ 1
2
1 11 1 12 2
2 21 1 22 2
β α 1
[Ф/м]
19

20.

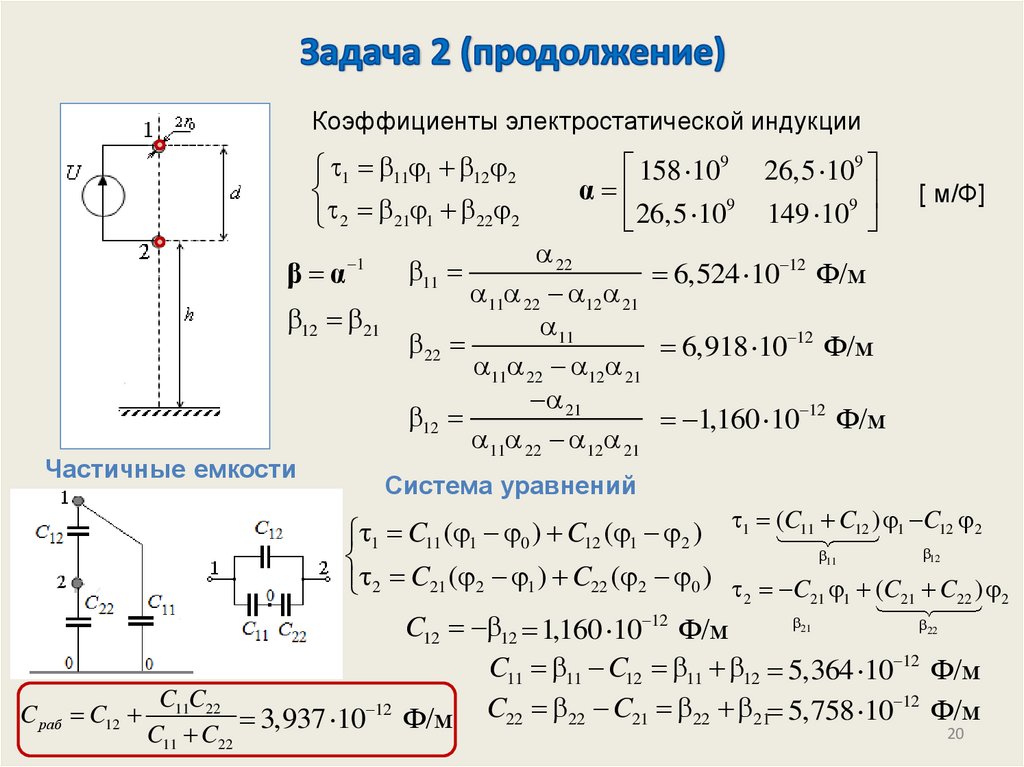
Коэффициенты электростатической индукции
1 11 1 12 2
2 21 1 22 2
β α 1
12 21
Частичные емкости
158 109
α
9
26,5 10
26,5 109
149 109
22
6,524 10 12 Ф/м
11 22 12 21
11
22
6,918 10 12 Ф/м
11 22 12 21
21
12
1,160 10 12 Ф/м
11 22 12 21
11
Система уравнений
(C11 C12 ) 1 C12 2
1 C11 ( 1 0 ) C12 ( 1 2 ) 1
2 C21 ( 2 1 ) C22 ( 2 0 ) 2 C21 1 (C21 C22 ) 2
C12 12 1,160 10 12 Ф/м
C11 11 C12 11 12 5,364 10 12 Ф/м
12
3,937 10 12 Ф/м C22 22 C21 22 21 5,758 10 Ф/м
11
21
C раб C12
C11C22
C11 C22
[ м/Ф]
12
22
20

21.

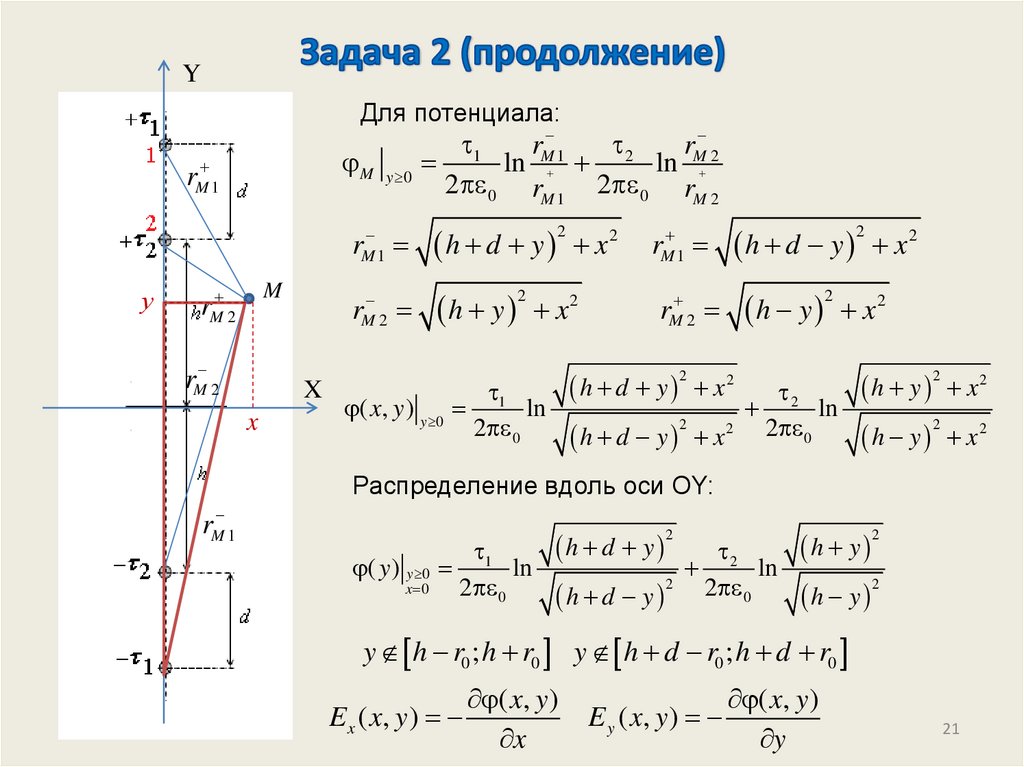
Y
Для потенциала:
M
rM 1
у
M
rM 2
rM 2
X
x
y 0
1
rM 1
2
rM 2
ln
ln
2 0 rM 1 2 0 rM 2
rM 1
h d y x2
rM 1
rM 2
h y
rM 2
2
( x, y ) y 0
2
x2
h d y x2
2
h y
h d y x2
2
h d y x2
2
1
ln
2 0
2
x2
2
ln
2 0
h y x2
2
h y x2
2
Распределение вдоль оси OY:
rM 1
( y ) y 0
x 0
1
ln
2 0
h d y
2
h d y
2
2
ln
2 0
h y
2
h y
2
y h r0 ; h r0 y h d r0 ; h d r0
E x ( x, y )
( x, y )
x
E y ( x, y )
( x, y )
y
21

22.

Распределение поверхностной плотности зарядов:
E y ( x, y )
( x, y )
y
1 1 2(h d y )
2(h d y )( 1)
2
2
2
2
2 0 2 x (h d y )
x (h d y )
2 1 2(h y )
2(h y )( 1)
2
2 0 2 x (h y ) 2 x 2 (h y ) 2
E1n E y ( x,0)
Изолированная система:
1 0
τ
1
2
2
1
2
1 U
φ
1
2
2
( x, y )
y
y 0
св ( x) 0 E1n 1св ( x) 2св ( x)
9
1
h d
1003
10
2
1св ( x) 2
Кл/м
2
x h d
x 2 64
2 h 627 10 9
2
2св ( x) 2
Кл/м
2
x h
x 2 25
22

23.

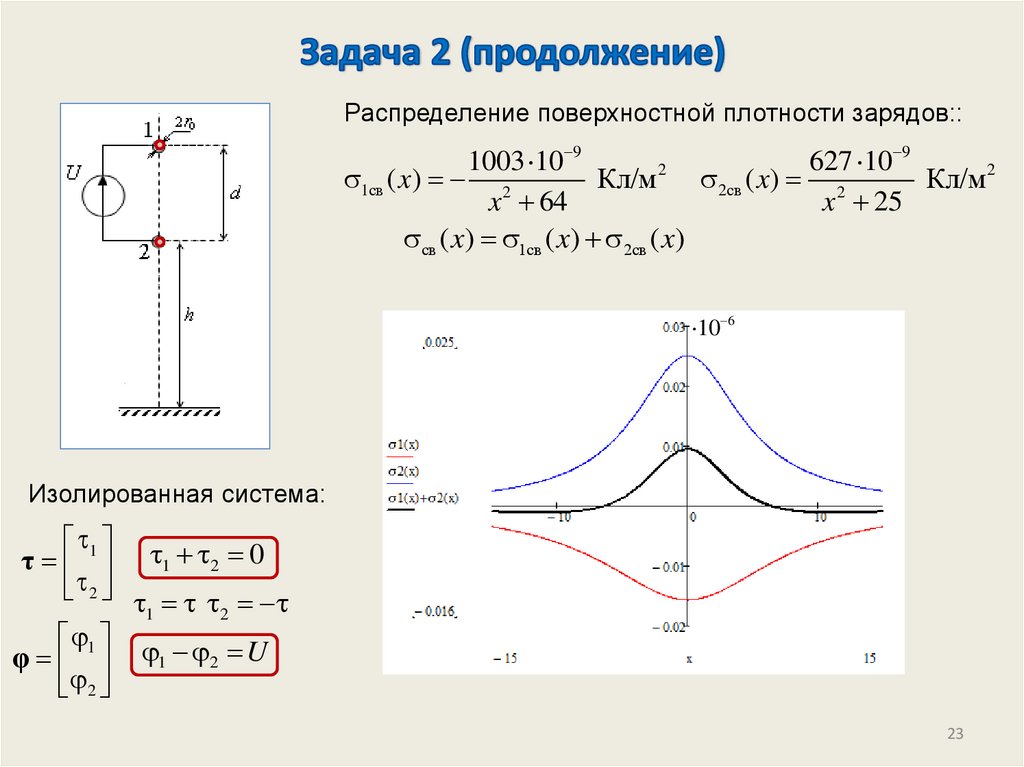
Распределение поверхностной плотности зарядов::
9
1003 10 9
627
10
1св ( x) 2
Кл/м 2 2св ( x) 2
Кл/м 2
x 64
x 25
св ( x) 1св ( x) 2св ( x)
10 6
Изолированная система:
1 0
τ
1
2
2
1
2
1 U
φ
1
2
2
23

24.

Дано: два провода радиусом
r0 2,5 мм подвешены параллельно
поверхности земли на высоте
h 5 м , расстояние между
проводами d 3 м . Между
проводами приложено
напряжение U 100 кВ.
Рассчитать линейную плотность
заряда на проводах ,
потенциалы проводов при
условии, что первый провод
заземлен. Двухпроводная линия
1-2 находится в однородном поле
грозовой тучи с напряженностью,
E0 2 кВ/м направленной
вертикально.
E0
Y
Метод зеркальных изображений + метод наложения
M
1 , 2
y 0
1
rM 1
2
rM 2
ln
ln + M
2 0 rM 1 2 0 rM 2
E0
y 0
E y dy E0 y
24

25.

Для потенциалов проводов:
1 = 11 1 + 12 2 E0 (h+d ) = 0
= U
2 = 21 1 + 22 2 E0 h
Потенциальные коэффициенты:
158 109
α
9
26,5
10
E0
26,5 109
149 109
[ м/Ф]
Линейная плотность зарядов:
Неизолированная система:
1
τ
2
1 2 0
φ 1
2
1 0
1 22,1 10 9 Кл/м
2 736,0 10 9 Кл/м
Проверка: 1 0 2 100000 B
Можно использовать β :
2 U
1 E0 (h+d ) = 11 1 + 12 2
1
2 E0 h = 21 1 + 22 2
2
1 11 1 12 2
2 21 1 22 2
25

26.

Для потенциала:
( y 8) 2 x 2
( y 5) 2 x 2
( x, y ) 198ln
6610ln
2 103 y
2
2
2
2
( y 8) x
( y 5) x
Распределение потенциала по оси OY:
E0
(0, y ) y 0 396ln
y 8
y 5
13220ln
2 103 y,
y 8
y 5
Распределение поверхностной плотности заряда:
Неизолированная система:
1
τ
2
1 2 0
φ 1
2
1 0
( x) 0 E y ( x,0) 0
(0, x)
y
132200 6336
2
( x ) 0
2000
Кл/м
2
2
64 x
25 x
2 U
26

27.

Распределение потенциала по оси OY:
Распределение поверхностной
плотности заряда:
27

28.

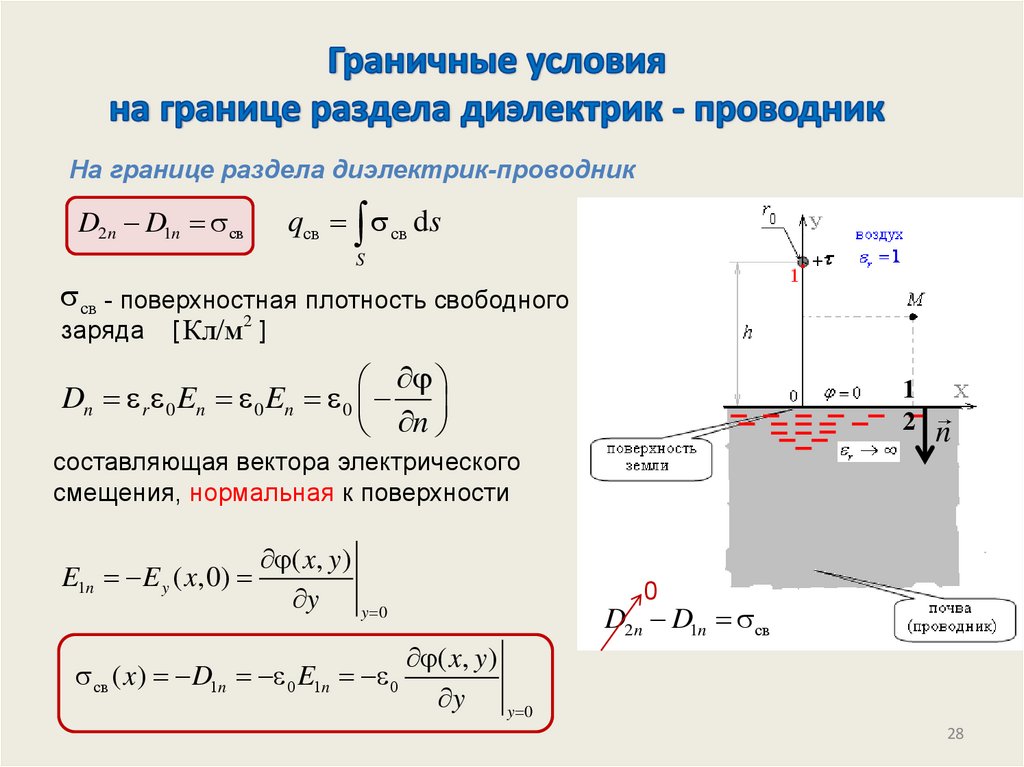
На границе раздела диэлектрик-проводник
qсв св ds
D2 n D1n св
S
св - поверхностная плотность свободного
заряда
[ Кл/м2 ]
Dn r 0 En 0 En 0
n
1
2
составляющая вектора электрического
смещения, нормальная к поверхности
E1n E y ( x,0)
( x, y )
y
0
D2 n D1n св
y 0
св ( x) D1n 0 E1n 0
n
( x, y )
y
y 0
28

29.

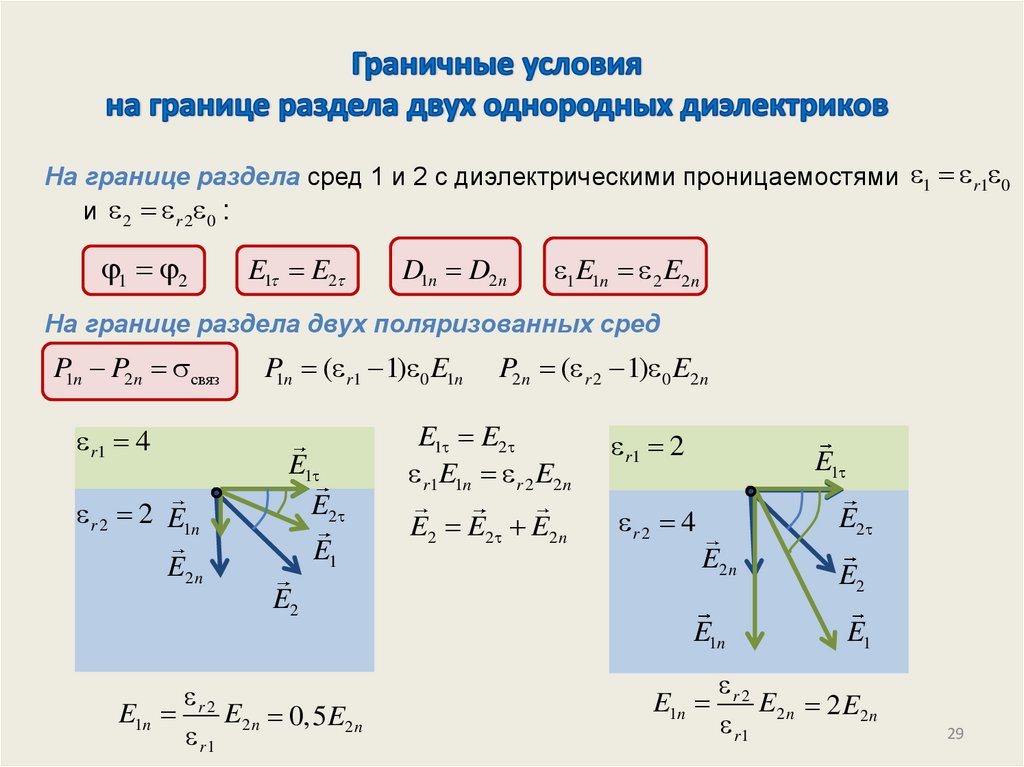
На границе раздела сред 1 и 2 с диэлектрическими проницаемостями 1 r1 0
и 2 r 2 0 :
1 2
E1 E2
D1n D2 n
1E1n 2 E2 n
На границе раздела двух поляризованных сред
P1n P2 n связ
r1 4
r 2 2 E1n
P1n ( r1 1) 0 E1n
E1
E2
E1
E2n
P2 n ( r 2 1) 0 E2 n
E1 E2
r1E1n r 2 E2 n
r1 2
E2 E2 E2n
r 2 4
E1
E2
E2n
E2
E1n
E1n r 2 E2 n 0,5 E2 n
r1
E1n
E2
E1
r 2
E 2 n 2 E2 n
r1
29

30.

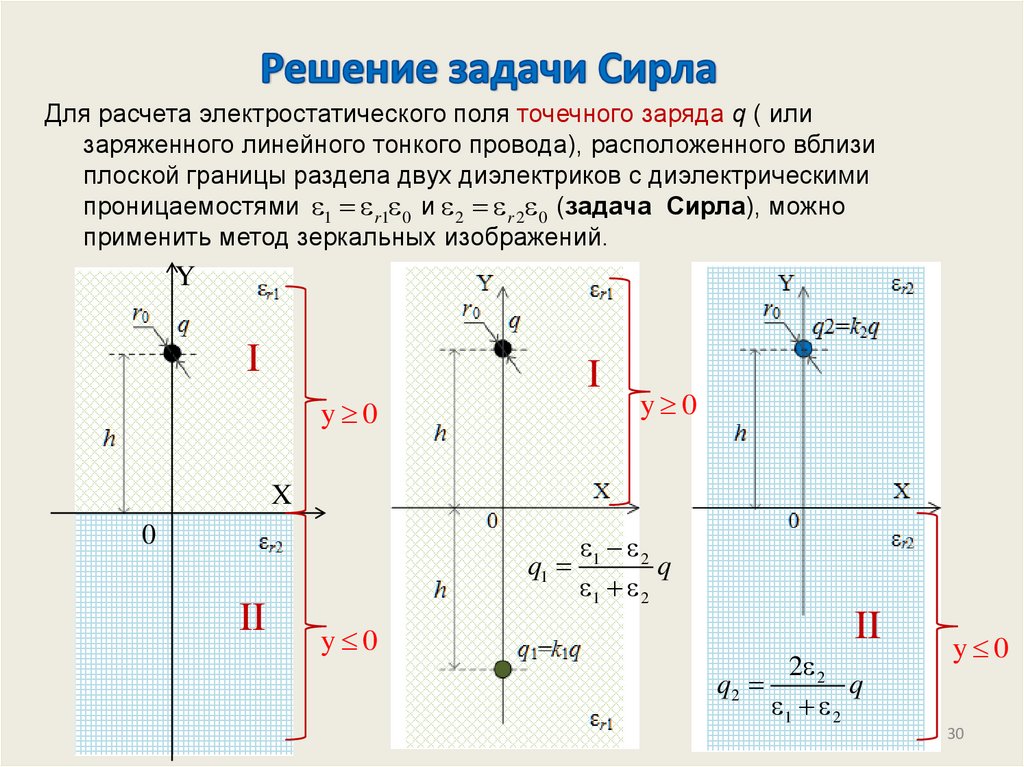
Для расчета электростатического поля точечного заряда q ( или
заряженного линейного тонкого провода), расположенного вблизи
плоской границы раздела двух диэлектриков с диэлектрическими
проницаемостями 1 r1 0 и 2 r 2 0 (задача Сирла), можно
применить метод зеркальных изображений.
Y
I
I
y 0
y 0
X
0
q1
II
y 0
1 2
q
1 2
II
2 2
q2
q
1 2
y 0
30

31.

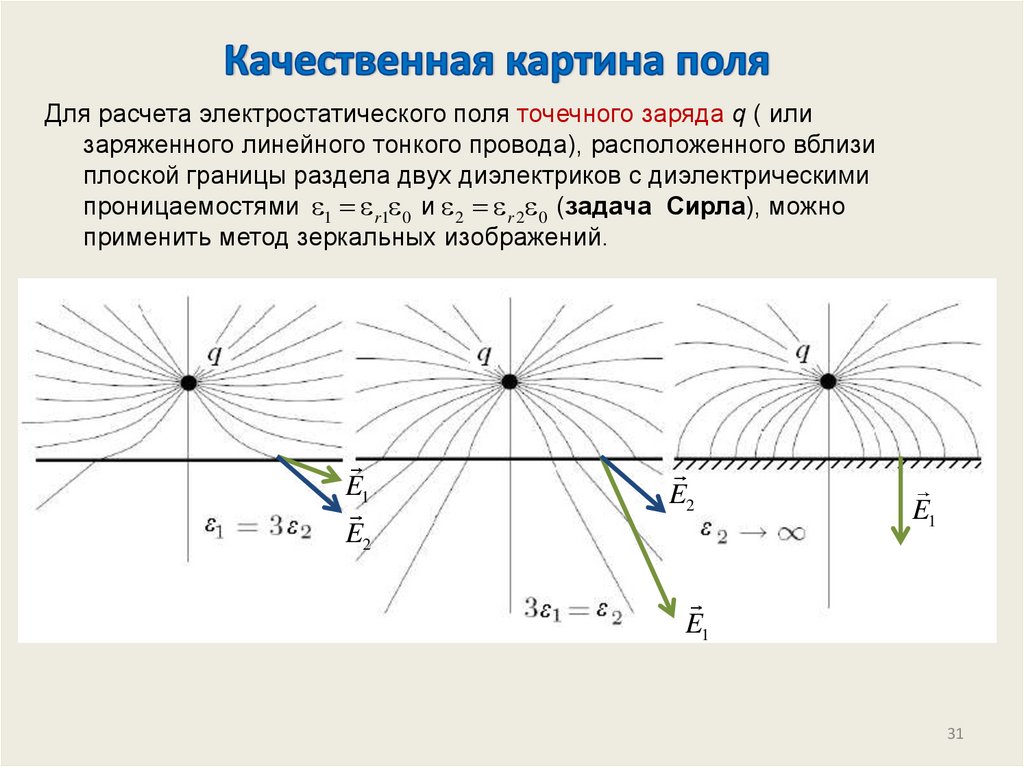
Для расчета электростатического поля точечного заряда q ( или
заряженного линейного тонкого провода), расположенного вблизи
плоской границы раздела двух диэлектриков с диэлектрическими
проницаемостями 1 r1 0 и 2 r 2 0 (задача Сирла), можно
применить метод зеркальных изображений.
E1
E2
E2
E1
E1
31

32.

Дано: Тонкий цилиндрический провод радиусом r0 20 мм
расположен параллельно на расстоянии h 30 cм от плоской
границы раздела двух однородных диэлектрических сред с r1 2
и r 2 6 . Линейная плотность заряда 800 нКл/м . Определить
потенциал провода, если (0) 0 . Как рассчитать поверхностную
плотность связанного заряда на границе двух диэлектриков связ ( x) ?
В однородной среде
I
у
( x, y )
r
x
II
Задача Сирла
1
ln С
2 r
1
ln
С
2
2
2
x (h y )
если (0) 0
(0,0)
С
1
ln С 0
2 h
1
ln
2 h
32

33.

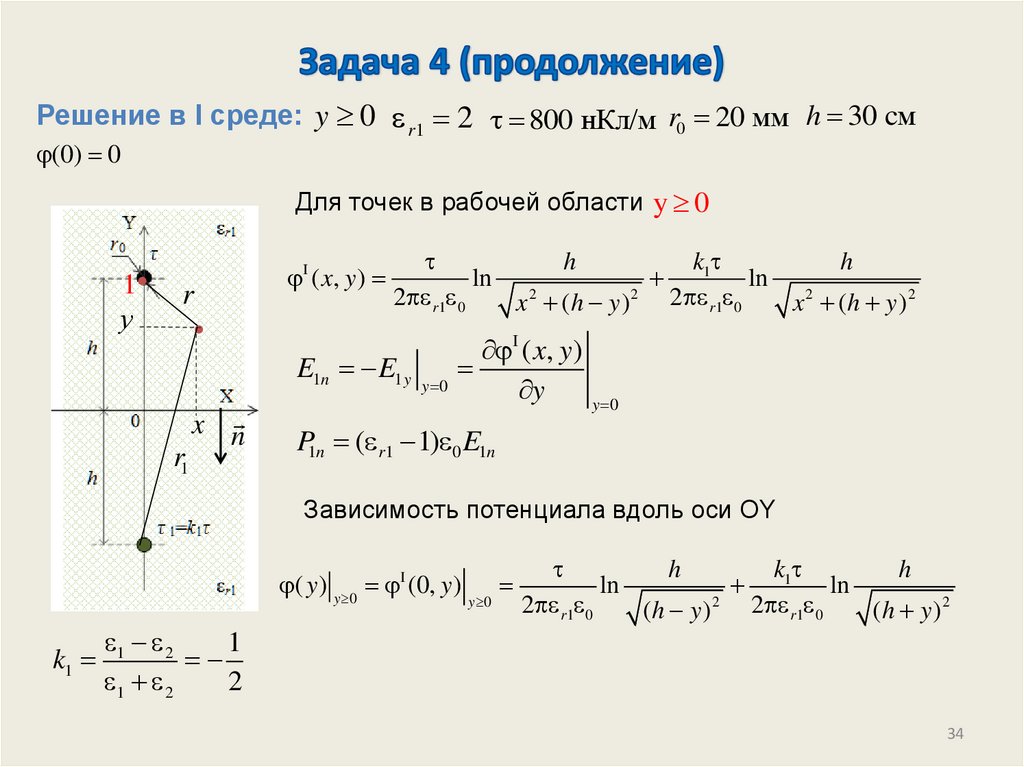
Решение в I среде: y 0 r1 2 800 нКл/м r0 20 мм h 30 cм
(0) 0
1
у
r
( k )
I
( )
Для точек в рабочей области y 0 1
1
k1
1
I ( x, y )
ln
ln С
2 r1 0 r 2 r1 0 r
1
k1
1
ln
ln
С
2
2
2
2
2 r1 0
2
x (h y )
x (h y )
r1 0
1
k1
1
(0,0)
ln
ln
С 0
Если (0) 0
2 r1 0 h 2 r1 0 h
x
r1
I ( x, y )
k1
1 2
1
1 2
2
h
k1
h
ln
ln
2 r1 0
x 2 (h y ) 2 2 r1 0
x 2 (h y ) 2
Потенциал провода
h
k1
h
1 I (0, h r0 )
ln
ln
2 r1 0 r0 2 r1 0 2h
800 10 9 30 ( 0,5) 800 10 9 30
1
ln
ln
38571,9 B
2 2 0 0,2
2 2 0
60
33

34.

Решение в I среде: y 0 r1 2 800 нКл/м r0 20 мм h 30 cм
(0) 0
Для точек в рабочей области y 0
1
у
r
I ( x, y )
h
k1
h
ln
ln
2 r1 0
x 2 (h y ) 2 2 r1 0
x 2 (h y ) 2
E1n E1 y
r1
x n
y 0
I ( x, y )
y
y 0
P1n ( r1 1) 0 E1n
Зависимость потенциала вдоль оси OY
( y ) y 0 I (0, y )
k1
1 2
1
1 2
2
y 0
h
k1
h
ln
ln
2 r1 0
(h y ) 2 2 r1 0
(h y ) 2
34

35.

Решение в II среде: y 0 r 2 6 (0) 0
( k )
II
Для точек в рабочей области y 0 2
II ( x, y )
r2
k2
1
k2
1
ln С II
ln
С II
2 r 2 0 r2
2 r 2 0
x 2 (h y )2
Если (0) 0 (0,0)
x
II ( x, y )
у
n
k2
1
ln С II 0
2 r 2 0 h
h
k2
ln
2 r 2 0
x 2 (h y ) 2
E2 n E2 y
y 0
II ( x, y )
y
y 0
P2 n ( r 2 1) 0 E2 n
2 2
3
k2
1 2 2
Зависимость вдоль оси OY
( y ) y 0 II (0, y )
y 0
k2
h
ln
2 r 2 0
(h y )2
35

36.

Распределение связанного поверхностного заряда связ ( x) P1n P2 n
Зависимость потенциала вдоль оси OY
h
k1
h
ln
ln
, y 0
2
2
2
2 r1 0
(h y )
(h y )
r1 0
( y )
k2
h
ln
, y 0
2
2 r 2 0
(h y )
Зависимость потенциала вдоль оси OХ
( x,0)
h
k1
h
k2
h
ln
ln
ln
2 r1 0
x 2 h 2 2 r1 0
x 2 h 2 2 r 2 0
x2 h2
E1n E1 y
E1 E1x
y 0
y 0
I ( x, y )
y
I ( x, y )
x
E2 n E2 y
y 0
E2 E2 x
y 0
y 0
y 0
II ( x, y )
y
II ( x, y )
x
y 0
r1E1n r 2 E2 n
E1 E2
y 0
36

37.

Автор доц. каф. ТОЭ НИУ «МЭИ»
Жохова М.П.
[email protected]
37