Похожие презентации:
Логарифмы
1. Логарифмы.
2.
Джон Непер - изобретатель системылогарифмов, основанной на установлении соответствия между арифметической и геометрической числовыми
прогрессиями.
В «Описании удивительной таблицы
логарифмов» он опубликовал первую
таблицу логарифмов (ему же
принадлежит и сам термин
«логарифм»). Объяснение таблицы
было дано в его сочинении
«Построение удивительной
таблицы логарифмов», вышедшем в
1619. Таблицы логарифмов, насущно
необходимые астрономам, нашли
немедленное применение.
Джон Непер
(1550-1617)
3. Основное логарифмическое тождество
4.
Определение логарифмаЛогарифмом положительного числа b по
основанию а, где а>0, а≠1, называется
показатель степени, в которую надо
возвести число а, чтобы получить b.
logab
a
=b
Это равенство называют основным
логарифмическим тождеством. Оно
справедливо при b>0, а>0, а≠1.
5.
Определение логарифмаИз определения логарифма следует, что
нахождение
x = logab
равносильно решению уравнения
x
a =b.
Например:
log28 = 3
,
потому что
23 = 8 .
6.
Используя основное логарифмическоетождество, найдите значения выражения
log317
3
=
log45
4
=
17
5
2log1316
13
=
-2log35
3
=
256
0,04
7.
ЛогарифмированиеЛогарифмированием называют действие
нахождения логарифма числа.
Читается: логарифм b по основанию a.
2
так как 5 =25
log525=2,
log4(1/16)=-2,
-2
так как 4 =1/16
log1/327 = -2,
-2
так как (1/3) =27
8.
Найдите значения выраженияlog5626= 4
log327= 3
log100,001= -3 log0,54= -2
log111= 0
log381= 4
9.
ЛогарифмированиеНайти логарифмы чисел b по основанию а
Ответ:
Ответ:
Ответ:
2,25
1,5
-5
10.
ЛогарифмированиеНайти x
По определению логарифма
Так как
Откуда
то
11.
При каких значениях х существуетлогарифм
Не существует
12. Доказательство основных свойств логарифмов
13.
Логарифм произведенияЛогарифм произведения положительных
чисел равен сумме логарифмов множителей
Пусть а>0, a=1, c>0. Тогда
(1)
Докажем справедливость формулы (1)
14.
Логарифм произведенияИзвестно:
(2)
(3)
Перемножим почленно равенства (2) и (3)
Формула (1) доказана
15.
Логарифм произведения16.
Логарифм частногоЛогарифм частного двух положительных
чисел равен разности логарифмов делимого
и делителя
Пусть а>0, a=1, c>0. Тогда
(1)
Докажем справедливость формулы (1)
17.
Логарифм частногоИзвестно:
(2)
(3)
Разделим почленно равенства (2) и (3)
Формула (1) доказана
18.
Логарифм частного19.
Логарифм степениЛогарифм степени с положительным
основанием равен показателю степени,
умноженному на логарифм основания
степени
Пусть а>0, b>0. r –любое действительное
число. Тогда
(1)
Докажем справедливость формулы (1)
20.
Логарифм степениВозводя основание логарифмического
тождества
в степень r получаем:
откуда по определению логарифма
следует формула (1):
21.
Логарифм степени22.
Переход к новому основаниюДля перехода от логарифма по одному
основанию к логарифму по другому
основанию используется формула:
(1)
где a>0, a≠1, b>0, c>0, c ≠1
Докажем справедливость формулы (1)
23.
Переход к новому основаниюЗапишем основное логарифмическое
тождество
Возьмем от обеих его частей логарифмы по
основанию с
Используя свойство логарифма степени,
получаем:
24.
Переход к новому основаниюСледствие.
При b=c –происходит перестановка
основания и логарифмируемого выражения
25.
Переход к новому основанию26. Свойства логарифмов
27.
a>0, a≠1, b>01)
Примеры:
log317
3
=
17;
2log1316
13
=
2
=16 = 256
log1316 2
(13
)=
28.
12)
a>0, a≠1
Пример:
1
0
3)
Пример:
0
a>0, a≠1
29.
4)a>0, a≠1, b>0, r-любое действительное
число
Пример:
a>0, a≠1, b>0
5)
Пример:
30.
6)a>0, a≠1, b>0, r - любое действительное
число
Пример:
31.
7)Пример:
a>0, a≠1, b>0,c>0
32.
8)Пример:
a>0, a≠1, b>0,c>0
33.
a>0, a≠1, b>0,c ≠19)
Пример:
34.
a>0, a≠1, b>0, b ≠110)
Пример:
35.
a>0, a≠1, c>011)
Пример:
36.
12)Пример:
a>0, a≠1, b>0
37.
a>0, c≠1, b>0,c>013)
Пример:
























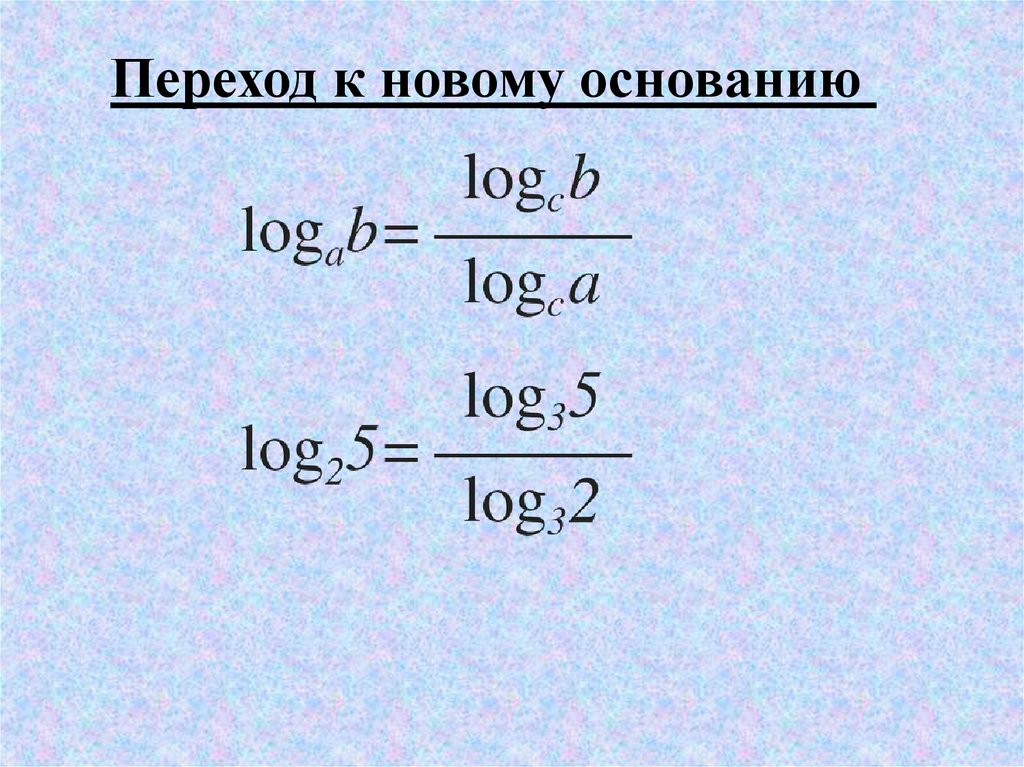

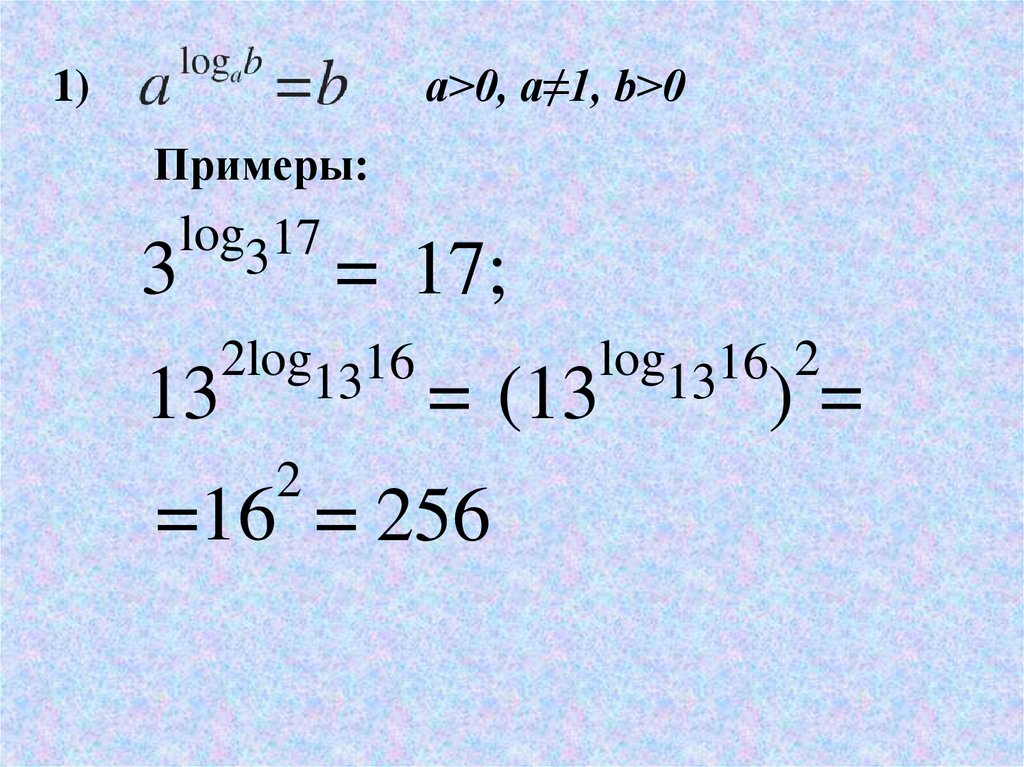
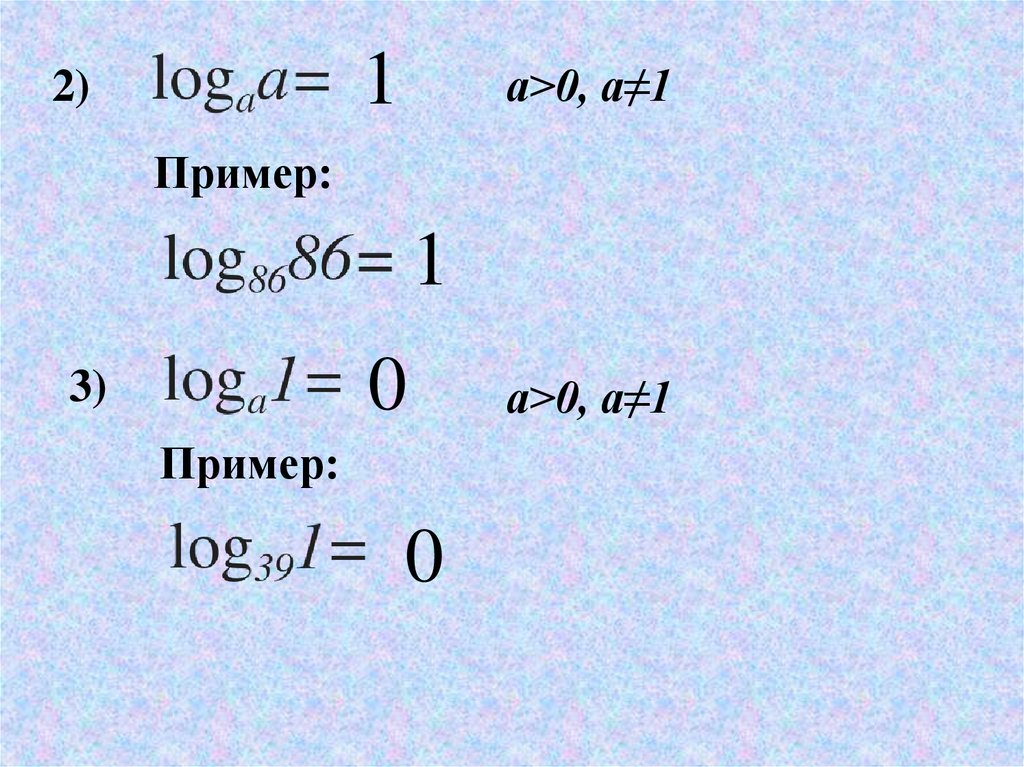
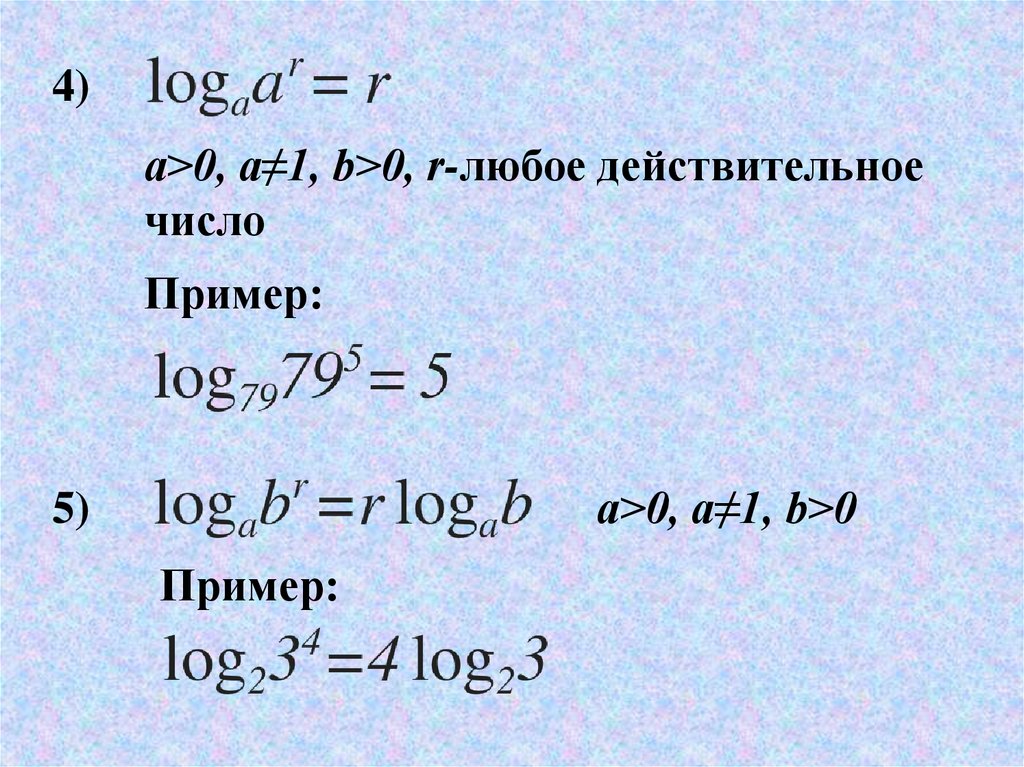
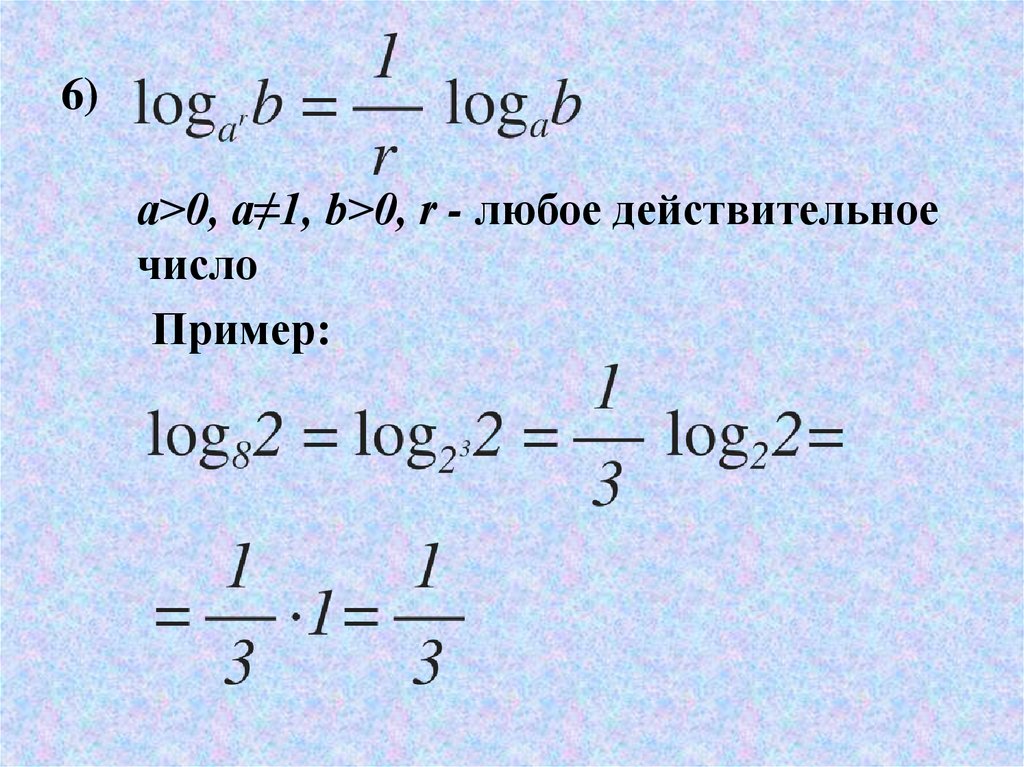
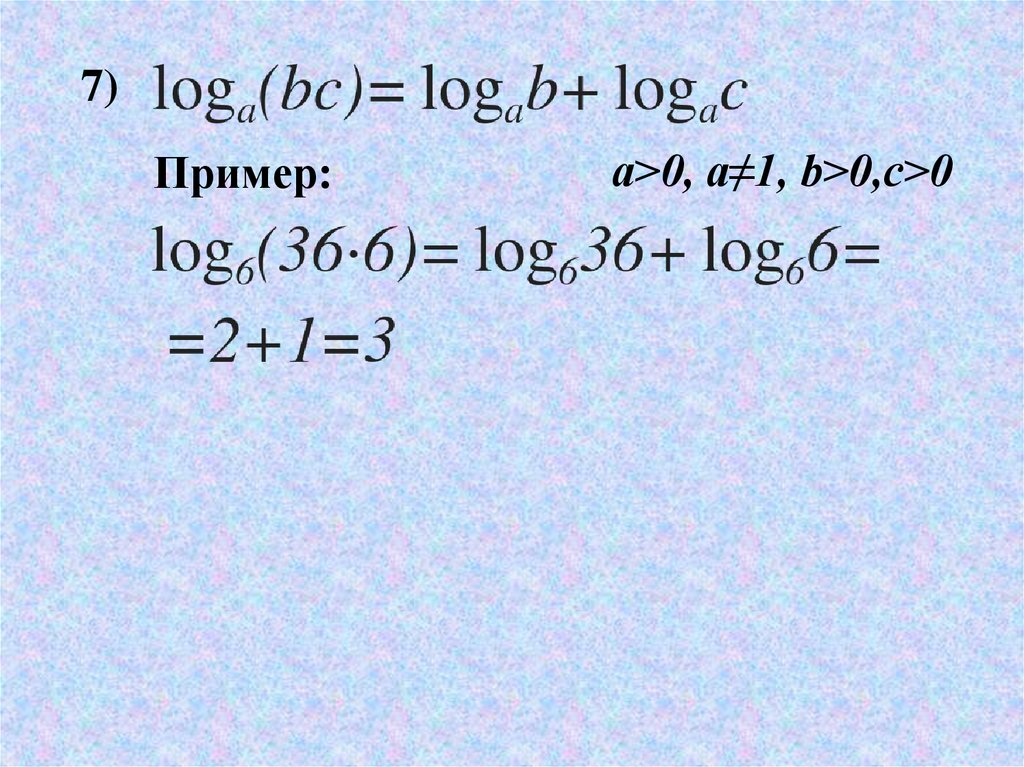
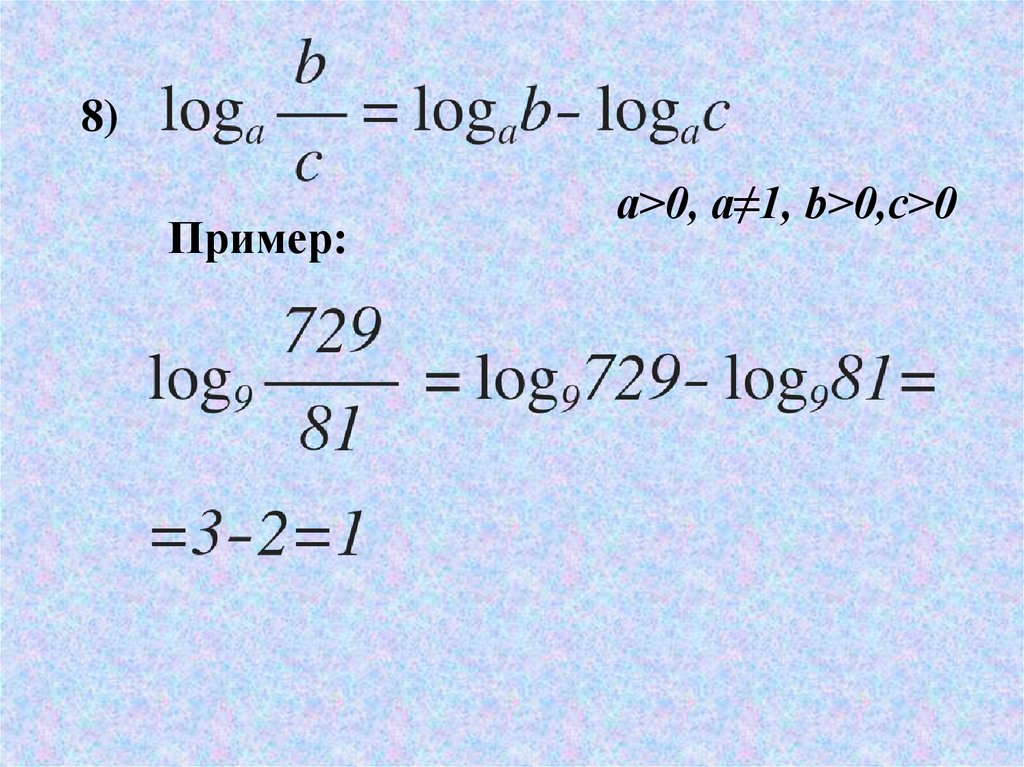
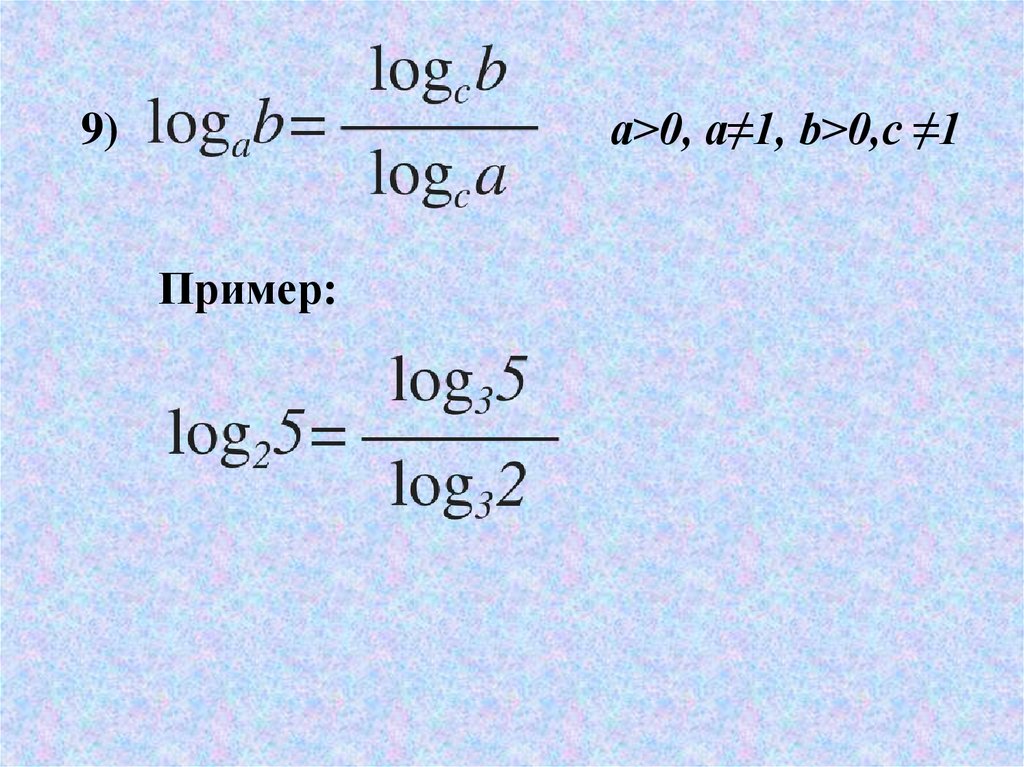
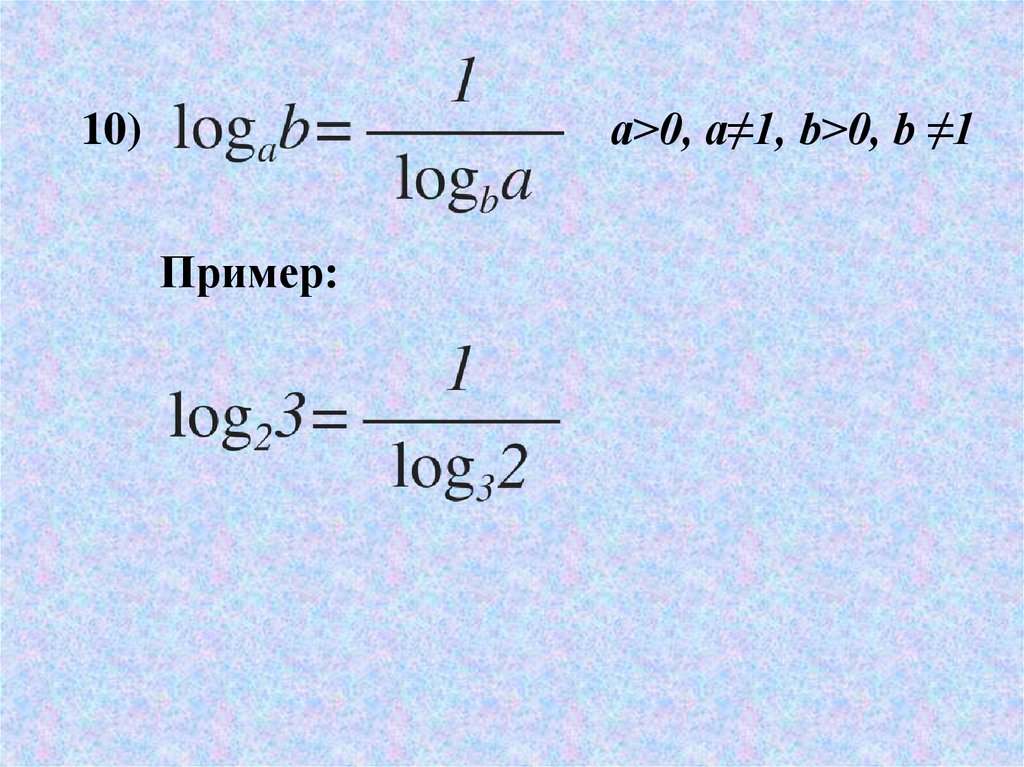
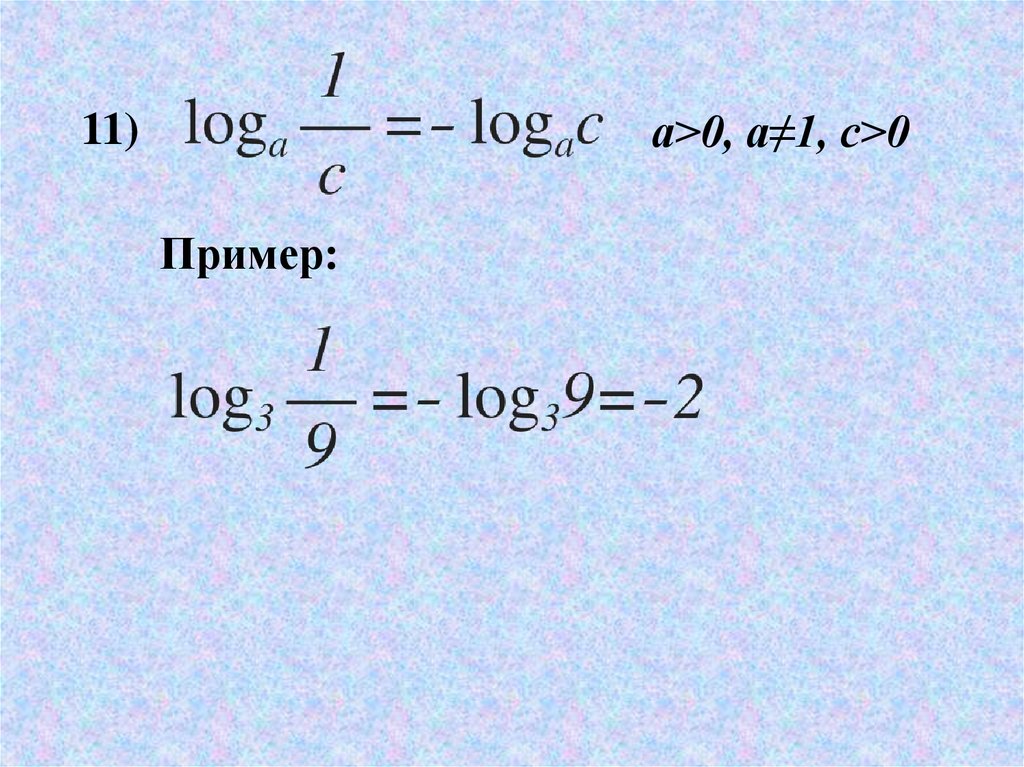
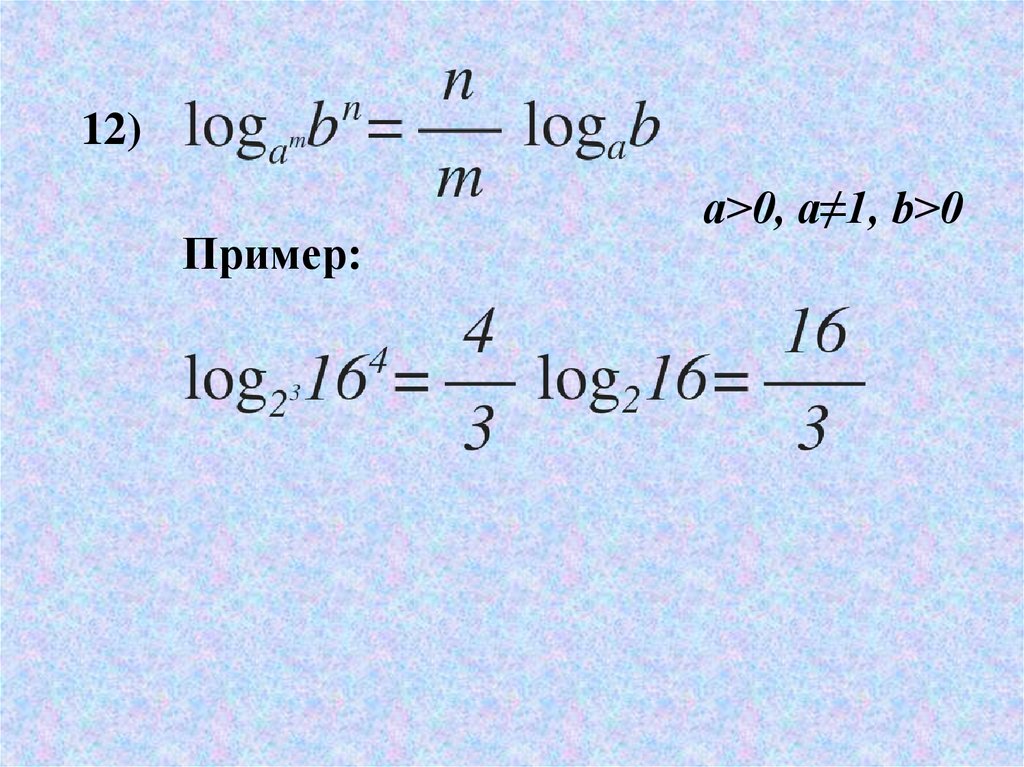
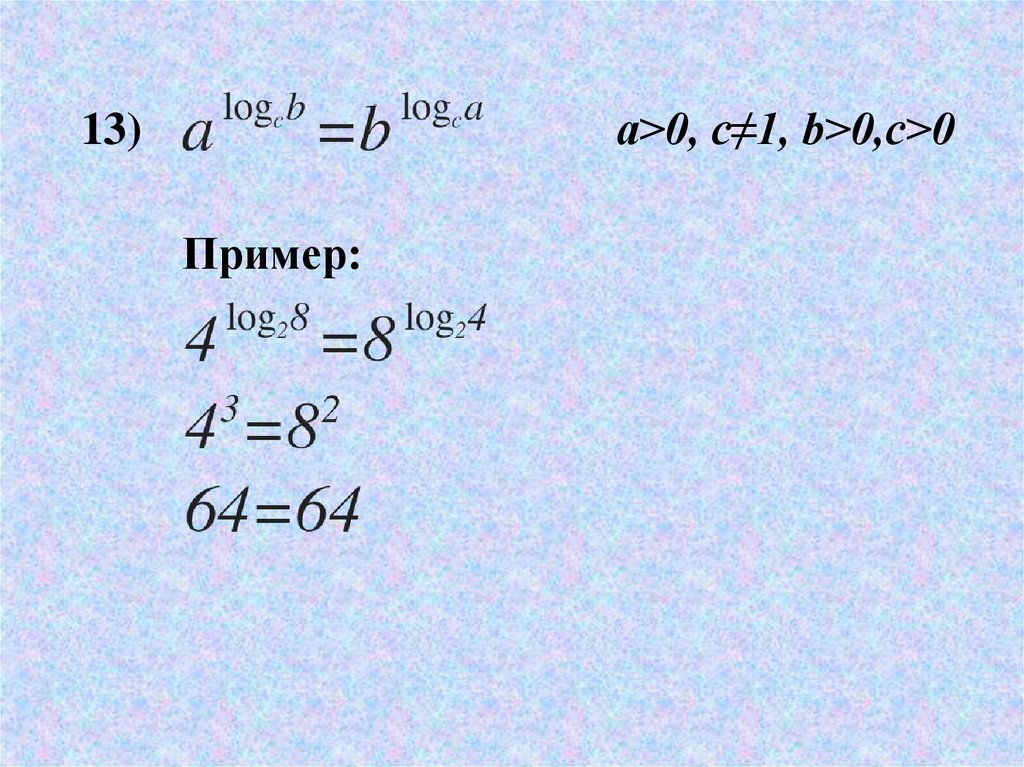
 Математика
Математика








