Пирамида. Элементы пирамиды. Виды пирамид

1.

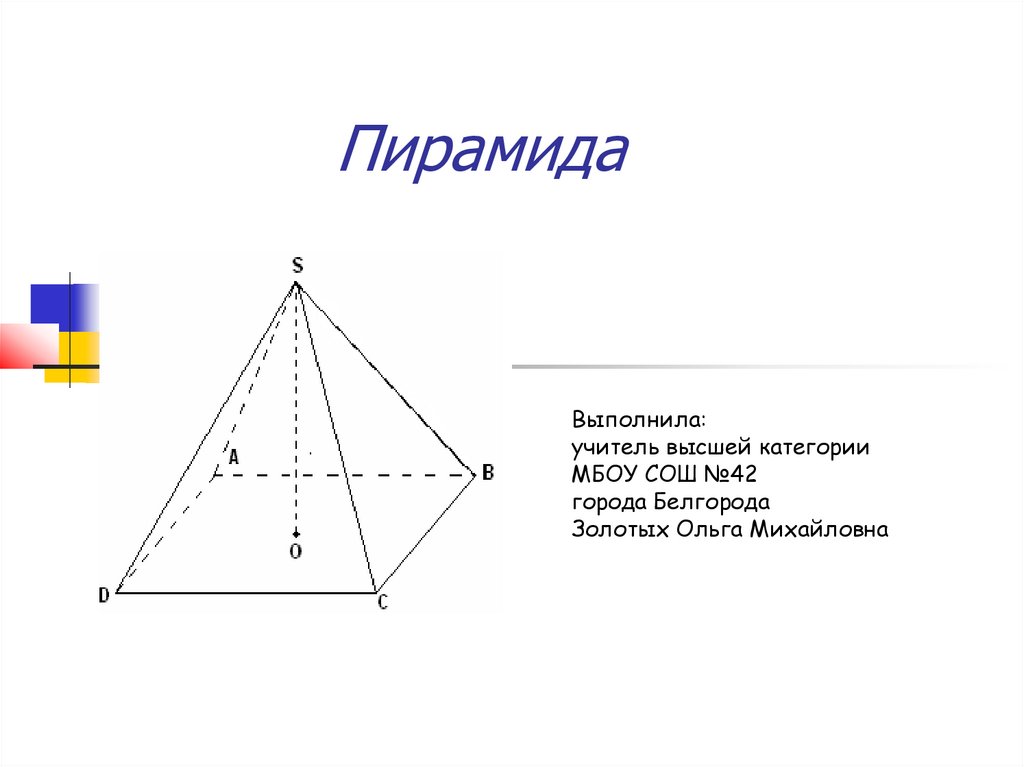
Пирамида
Выполнила:
учитель высшей категории
МБОУ СОШ №42
города Белгорода
Золотых Ольга Михайловна

2.

ЧТО ТАКОЕ ПИРАМИДА?
Первые определения этому понятию давали:
Евклид Телесная фигура, ограниченная плоскостями, которые от
одной плоскости (основания) сходятся к одной точке(вершине)
Герон Фигура, ограниченная треугольниками, сходящимися в
одной точке, и основанием которой служит многоугольник
Учебники XIXв. Телесный угол, пересечённый плоскостью
Тейлор Многогранник, у которого все грани, кроме одной,
сходятся в одной точке
Лежандр Телесная фигура, образованная треугольниками,
сходящимися в одной точке и заканчивающаяся по различным
сторонам плоского основания

3.

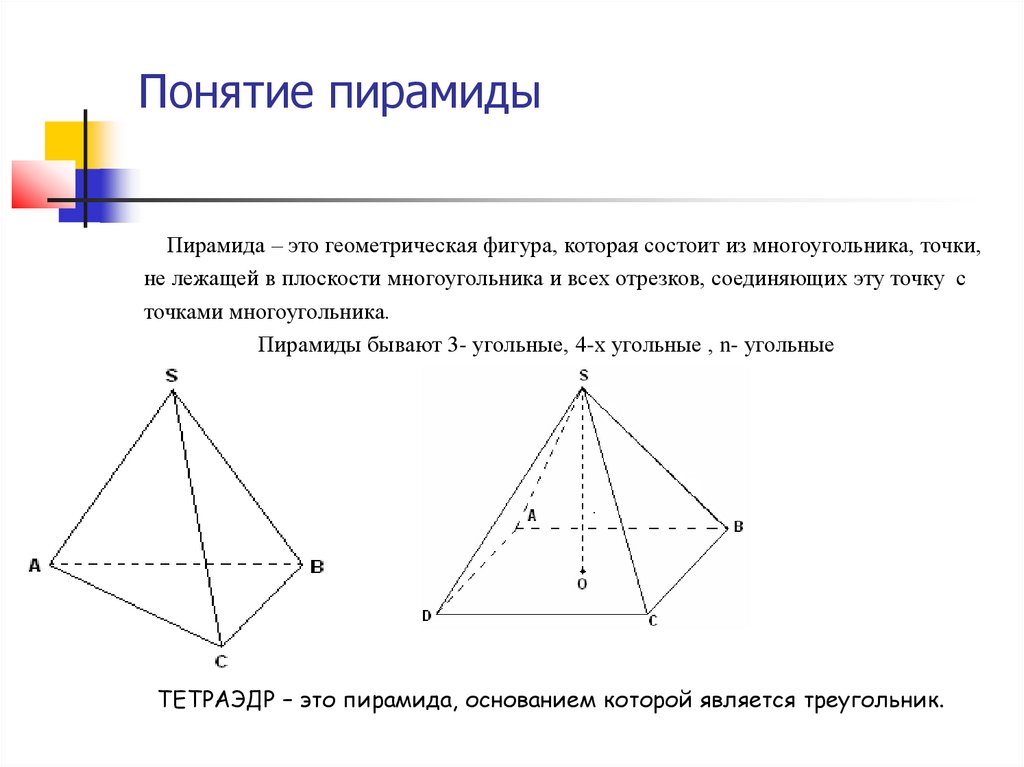
Понятие пирамиды
Пирамида – это геометрическая фигура, которая состоит из многоугольника, точки,
не лежащей в плоскости многоугольника и всех отрезков, соединяющих эту точку с
точками многоугольника.
Пирамиды бывают 3- угольные, 4-х угольные , n- угольные
ТЕТРАЭДР – это пирамида, основанием которой является треугольник.

4.

Элементы пирамиды.
S – вершина пирамиды.
АВС – основание пирамиды.
АВ, АС, ВС – ребра основания.
SA, SB, SC – боковые ребра.
SAC, SBC, SAB – боковые грани
А, В, С – вершины основания
Условные обозначения
Sб - площадь боковой поверхности пирамиды
Sп – площадь полной поверхности
V – объем пирамиды
H – высота пирамиды
h – апофема правильной пирамиды

5.

Развертка треугольной пирамиды
Формулы
Sб = S1 + S2 + S3 + …
Sn = Sб + Sосн
V = 1 Sосн . H
3
H – высота пирамиды.
Высота пирамиды – это перпендикуляр, опущенный из вершины
пирамиды на плоскость основания

6.

Это надо знать! Виды пирамид
Пирамида с равными боковыми ребрами или равными углами наклона
боковых ребер к плоскости основания; проекцией вершины пирамиды
является центр описанной около многоугольника окружности.
О – центр описанной окружности. В произвольном
треугольнике R=
=
abc
4S
a
2 sin

7.

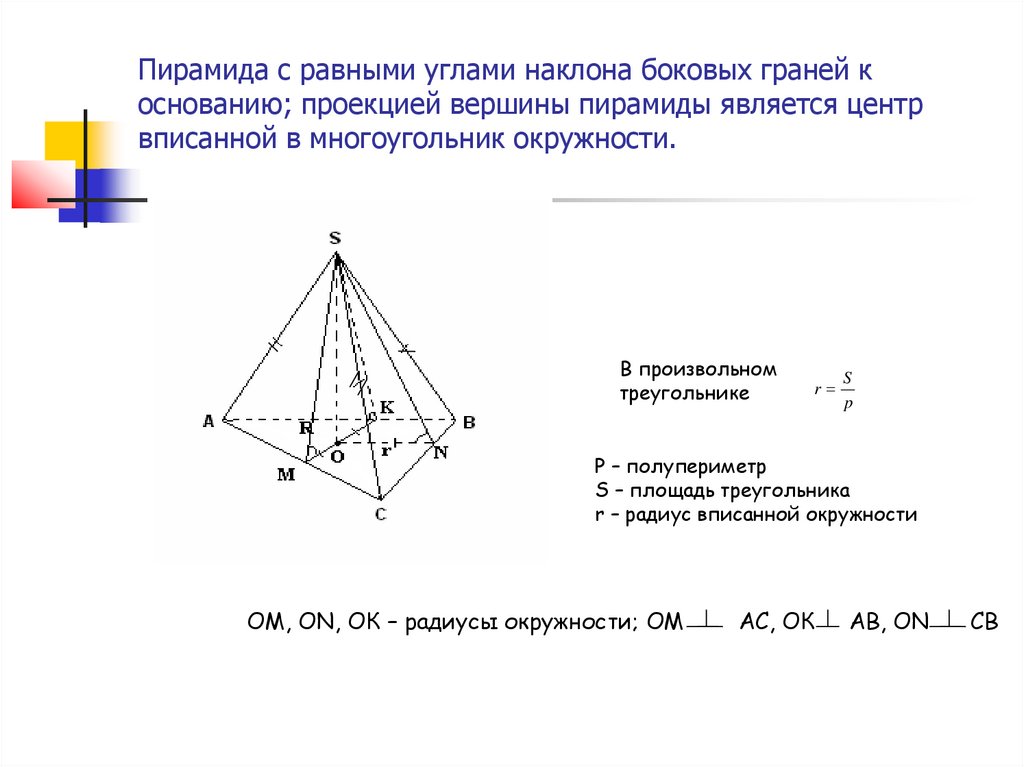
Пирамида с равными углами наклона боковых граней к
основанию; проекцией вершины пирамиды является центр
вписанной в многоугольник окружности.
В произвольном
треугольнике
r
S
p
Р – полупериметр
S – площадь треугольника
r – радиус вписанной окружности
ОМ, ОN, ОК – радиусы окружности; ОМ
АС, ОК
АВ, ОN
СВ

8.

Пирамида с 1 одним боковым ребром, перпендикулярным основанию или
пирамида с 2-мя смежными боковыми гранями, перпендикулярными
основанию; проекцией вершины пирамиды является вершина основания,
принадлежащая этому боковому ребру.

9.

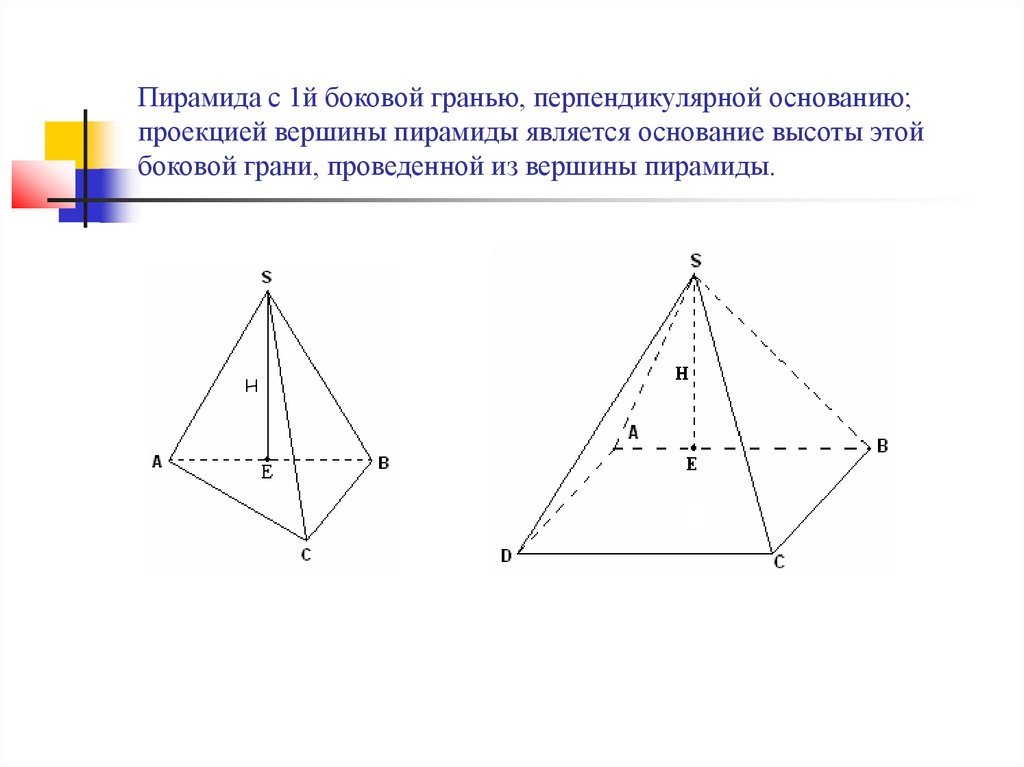
Пирамида с 1й боковой гранью, перпендикулярной основанию;
проекцией вершины пирамиды является основание высоты этой
боковой грани, проведенной из вершины пирамиды.
Н

10.

Пирамида с 2-мя противолежащими боковыми гранями,
перпендикулярными плоскости основания.
SABCD – пирамида
SE - высота
H
Н

11.

Правильная пирамида
Правильная пирамида – это пирамида, у
которой в основании лежит правильный
многоугольник и проекцией вершины
пирамиды является центр этого
многоугольника.
b
Н
h
Н
Н
a
n a h
2
S
б
n b sin
2
S
б
2
n- число углов пр.
Апофема правильной пирамиды - это высота боковой грани,
проведенная из вершины пирамиды.
Правильный тетраэдр – это правильная пирамида, у которой все
ребра равны.
пирамиды
- плоский угол при вершине

12.

Сечения пирамиды
Сечение пирамиды плоскостью, параллельной основанию - это
многоугольник, подобный основанию. Этим сечением пирамида
разбивается на 2 фигуры: пирамиду и усеченную пирамиду.
S
S
2
2
S О1 А1 S О1
к
S ОА SО
сеч
А1
В1
О1
2
осн
О1
С1
А
Sб = S1трапеции + S2трапеции + S3трапеции +. . .
Sп = Sб + Sосн + Sсеч
В
О
О
В
А
1
V h Sосн
3
S S
осн
сеч
Sсеч
С
Боковые грани усеченной пирамиды – трапеции
Sтр= а в h
2

13.

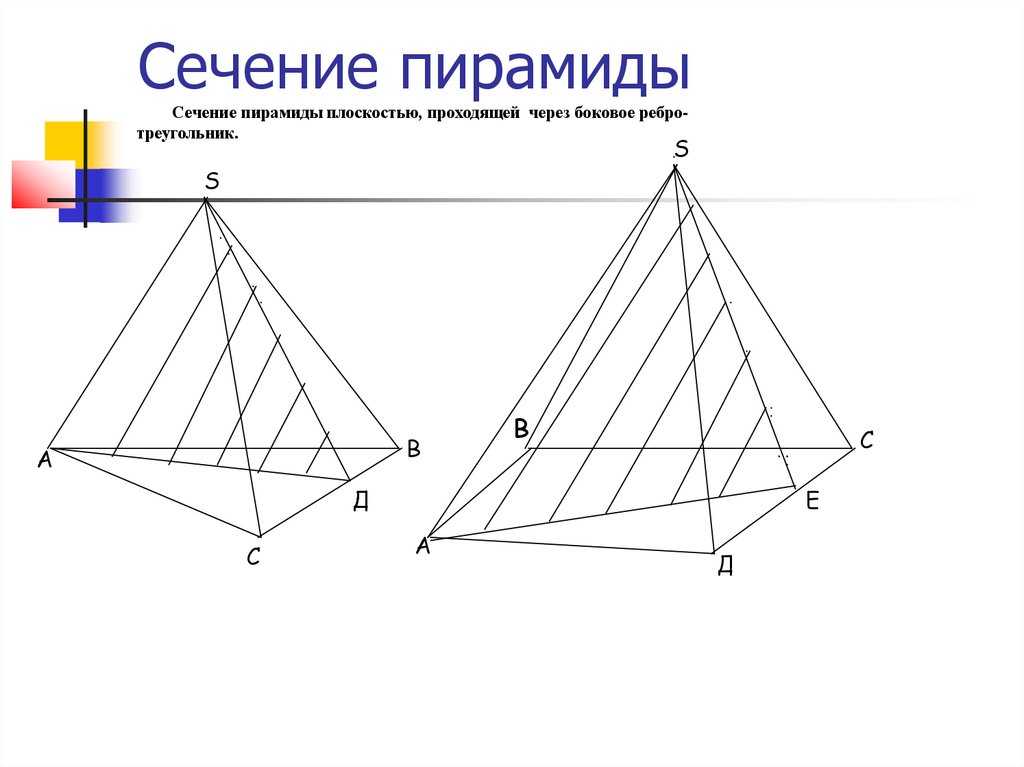
Сечение пирамиды
Сечение пирамиды плоскостью, проходящей через боковое ребротреугольник.
S
S
В
А
В
С
Д
С
Е
A
Д

14.

Сечение пирамиды
А
Сечение пирамиды произвольной плоскостью – многоугольник. Основная задача следов:
В
Х
В1
А1
А
S
А→А1
В→В1
АВ∩А1В1 = Х; точка Х є следу. Аналогично находится точка Y.
След – прямая пересечения секущей плоскости и плоскости
основания. Если одна из точек, через которую проходит
сечение, лежит в основании, то через нее проходит след.
Дано:
SАВСД – пирамида
P
М є (SВС), N є (SC), К є (SAB).
S
S
Построить сечение пирамиды плоскостью.
проходящей через точки М, N, и К.
K
Решение.
P
P
Q
R
M
A
B
K1
D
A
C
D
x
Е
N
C
B
M1
Y
М → М1, М1 є ВС,
N→ С, К →К1; К1 є АВ,
МN ∩ М1С = Х; КМ ∩ К1М1 = Y; XY- след.
MN ∩ (SBC) = NR; R є SB;
RK є (SAB) = RP; P є SA;
AD ∩ XY = E; PЕ ∩ (SAD) = PQ; Q є SD;
NQ ∩ (SCD) = NQ.
NRPQ- искомое сечение.