Пирамида. Виды пирамид. Решение задач

1.

Задача на слайде 7.3.
Дано:
МАВСДЕ – пирамида
АМ = 12
Найти: МО, АО, СО, МС
Решение
Рассмотрим
300
МС = 2МО (свойство катета, лежащего против угла в 300)
Ответ:
В боковых ребрах.
Вывод: Если в пирамиде все боковые ребра равны, то около основания пирамиды можно описать окружность и вершина пирамиды проектируется в центр этой окружности.
К углу наклона бокового ребра к плоскости основания.
Вывод: Если все ребра пирамиды одинаково наклонены к плоскости основания, то:
Около основания пирамиды можно описать окружность и вершина пирамиды проектируется в центр этой окружности.
Около такой пирамиды можно описать шар. Центр описанного шара лежит на прямой, содержащей высоту шара..
Задача со слайда 7.4
Дано:
МАВСДN – пирамида
Найти: МК, ОК, МЕ, ОЕ
Решение
1. Рассмотрим М
Рассмотрим 6
МЕ = 2МО (свойство катета, лежащего против угла в 300)
МЕ = 12
Ответ:
Диктант
Дано:
МАВС – пирамида
МА = МВ = МС = 6,25
АС = АВ = 5
ВС =6
Найти: Н; V
Решение
Так как МА = МВ = МС, то ОА = ОВ = ОС = R
По формуле Герона
Итак,
Рассмотрим
По следствию из теоремы Пифагора ;
Рассмотрим
Ответ:
МАВС – пирамида
ВС = 13 АС = 14 АВ =15
Найти: Н; Sбок; V
По материалам учебника
Л.С. Атанасян «Геометрия» § 2 п.28;29.
боковых ребрах.
Вывод: Если в пирамиде все боковые ребра равны, то около основания пирамиды можно описать окружность и вершина пирамиды проектируется в центр этой окружности.
К углу наклона бокового ребра к плоскости основания.
Вывод: Если все ребра пирамиды одинаково наклонены к плоскости основания, то:
Около основания пирамиды можно описать окружность и вершина пирамиды проектируется в центр этой окружности.
Около такой пирамиды можно описать шар. Центр описанного шара лежит на прямой, содержащей высоту шара..
Задача со сл
2003

2.

План урока:
Определение пирамиды
(§ 28 стр. 65)
Элементы пирамиды
(§ 28 стр. 66)
Правильные пирамиды
(§ 29 стр. 66)

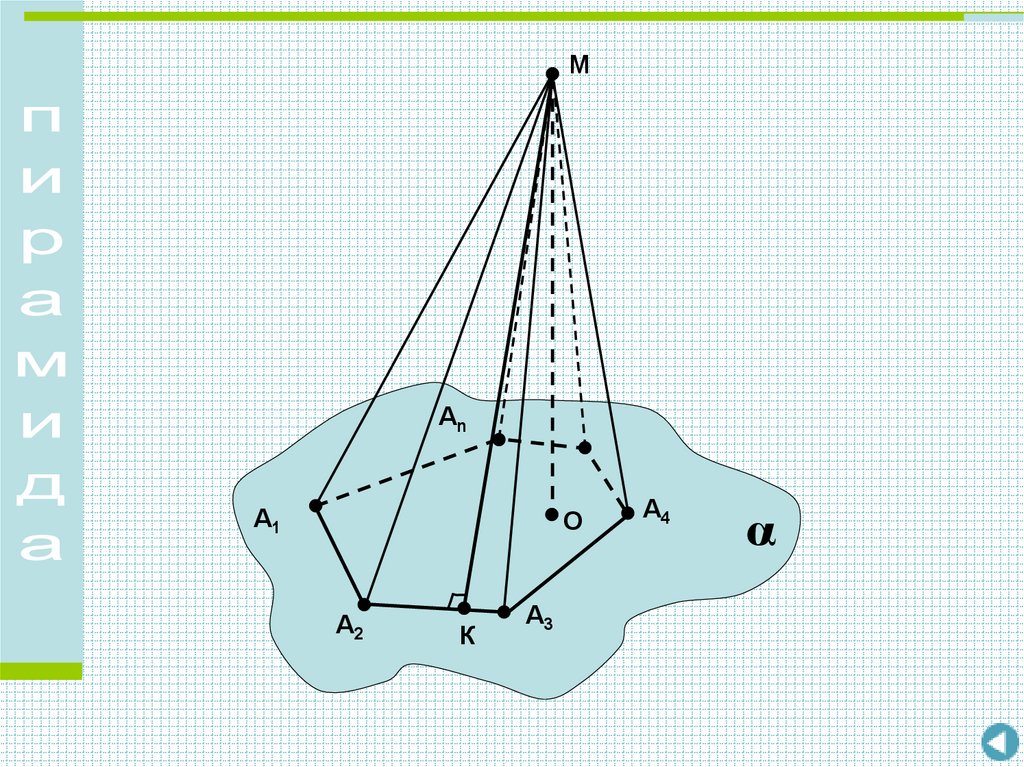
3.

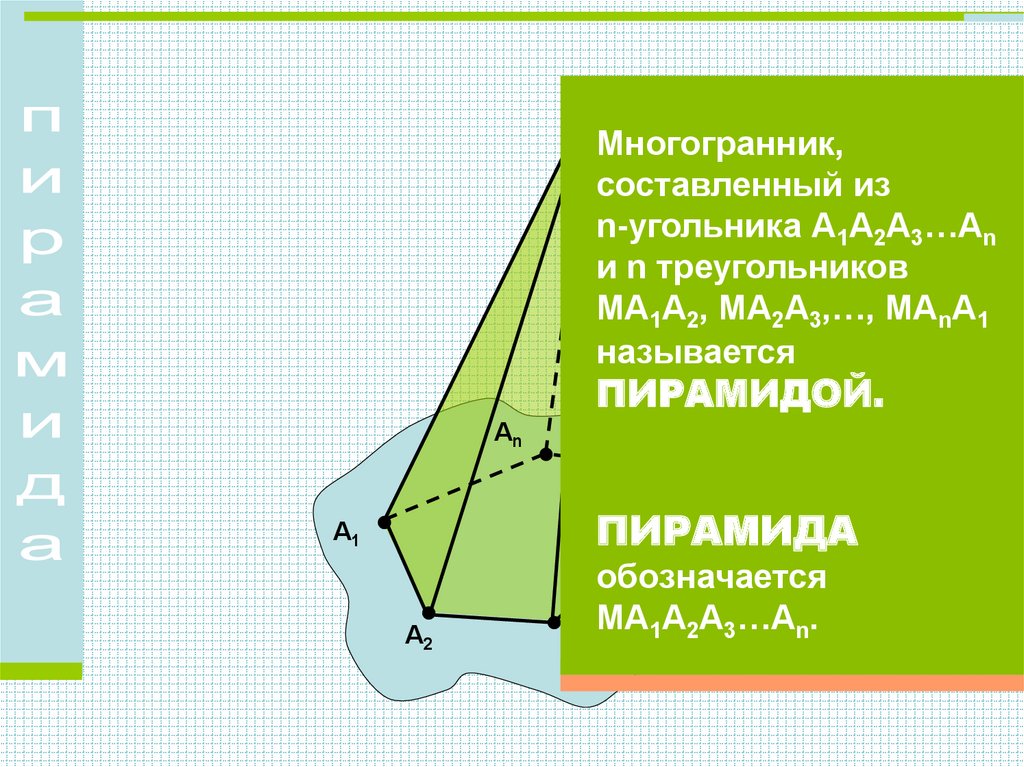
М
Многогранник,
составленный из
n-угольника А1А2А3…Аn
и n треугольников
МА1А2, МА2А3,…, МАnА1
называется
ПИРАМИДОЙ.
Аn
А4
ПИРАМИДА
α
А1
А2
обозначается
А3МА1А2А3…Аn.

4.

Слово «пирамида» в геометрию ввели греки,
которые, как полагают, заимствовали его у египтян,
создавших самые знаменитые пирамиды на свете.

5.

«Пирос» по-гречески рожь. Считают, что греки
выпекали хлебцы, имевшие форму пирамиды.

6.

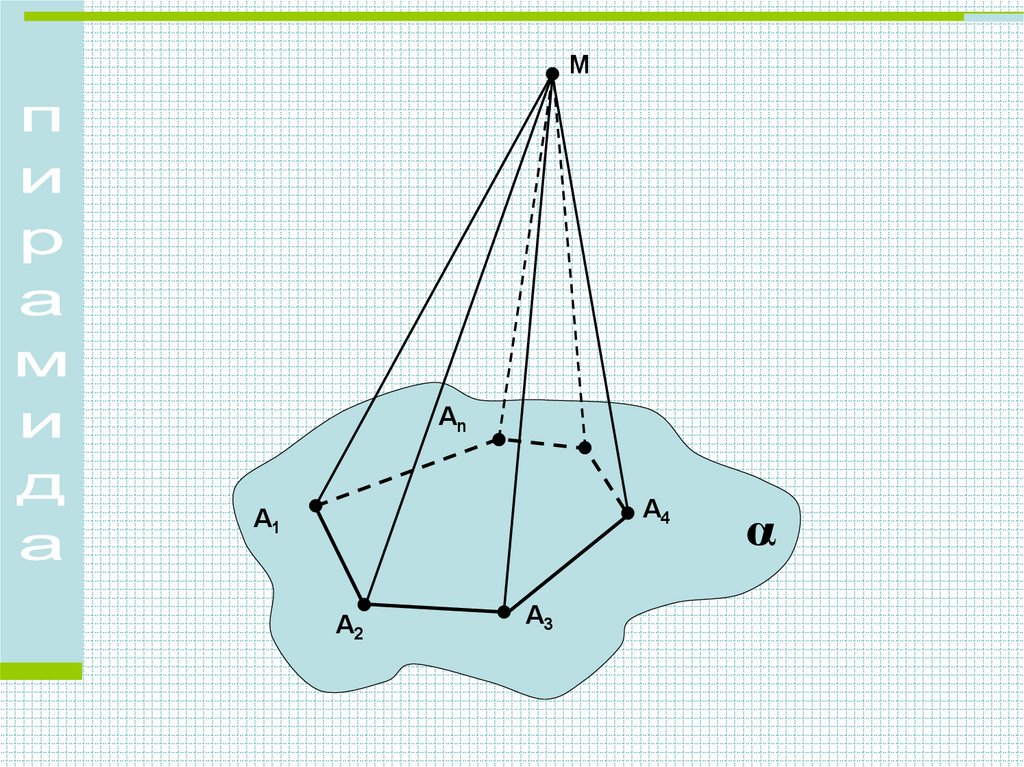
Элементы пирамиды
Вершина пирамиды: М
1 Вершины
Вершины основания пирамиды: А1, А2, А3,…
2 Ребра
Боковые ребра: МА1, МА2, МА3,…
Ребра основания: А1А2, А2А3, А3А4,…
3 Грани
Основание: А1А2А3…Аn
Боковые грани: ∆А1МА2, ∆А2МА3,…
4 Высоты
Высота пирамиды МО┴(А1А2А3), МО=Н
Высота боковой грани: (МК┴А2А3, МК=h)
n+1
2n
n+1
n+1
Плоский угол при вершине пирамиды: LА1МА2,
LА2МА3,…
5 Углы
Угол наклона бокового ребра к плоскости
основания (угол при ребре МА1): LMA10
Двугранный угол при ребре основания (угол
наклона боковой грани к основанию): LMKO
n

7.

М
Аn
А4
А1
А2
А3
α

8.

М
Аn
А4
А1
А2
А3
α

9.

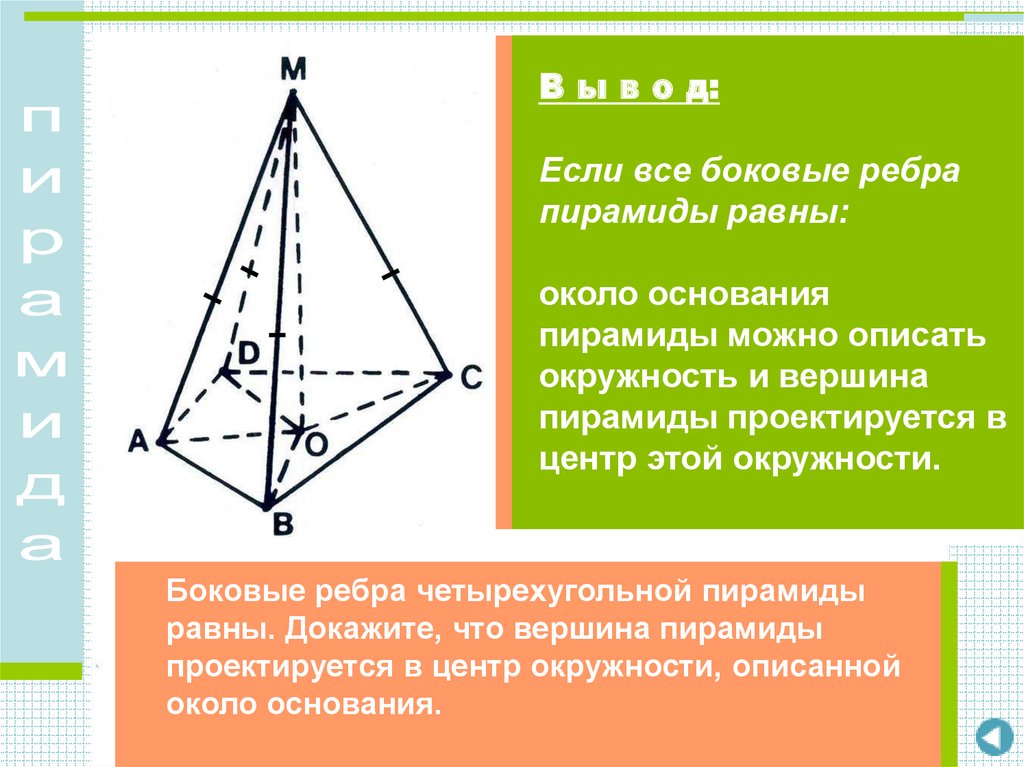
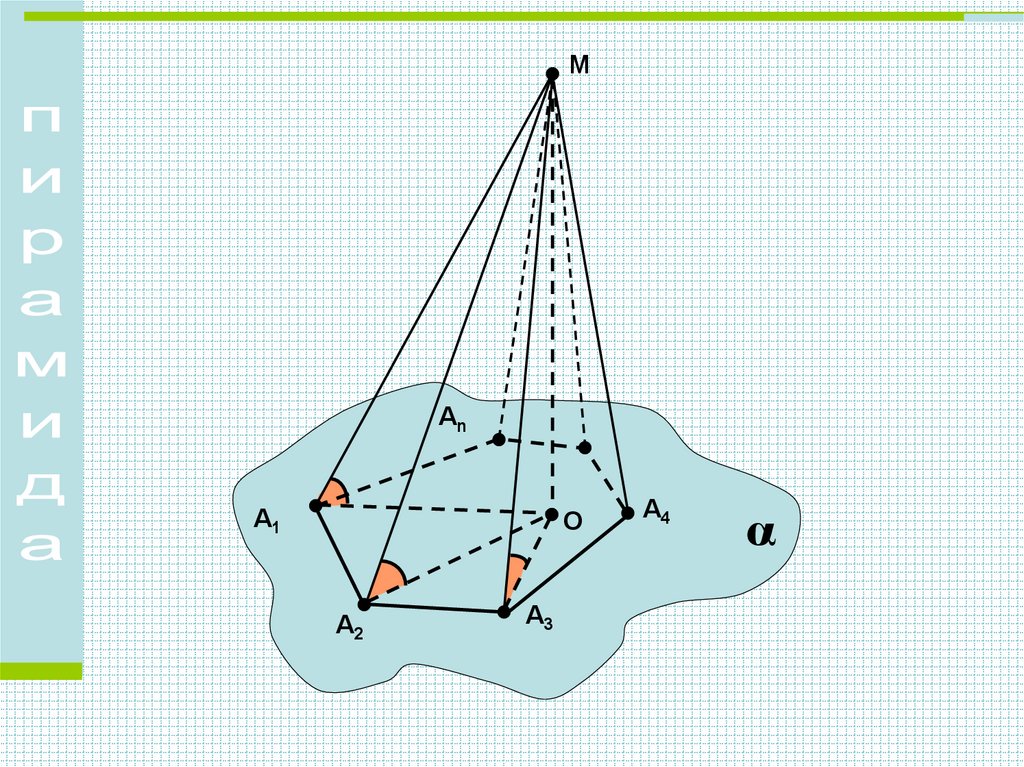
В ы в о д:
Если все боковые ребра
пирамиды равны:
около основания
пирамиды можно описать
окружность и вершина
пирамиды проектируется в
центр этой окружности.
Боковые ребра четырехугольной пирамиды
равны. Докажите, что вершина пирамиды
проектируется в центр окружности, описанной
около основания.

10.

М
Аn
А4
А1
А2
А3
α

11.

М
Аn
А1
О
А2
К
А3
А4
α

12.

М
Аn
А4
А1
А2
А3
α

13.

М
Аn
А1
О
А2
А3
А4
α

14.

Боковые ребра пирамиды наклонены к
плоскости основания под одним углом.
Докажите, что вершина пирамиды
проектируется в центр окружности, описанной
около основания пирамиды.

15.

В ы в о д:
Если все ребра пирамиды
одинаково наклонены к
плоскости основания, то:
около основания
пирамиды можно описать
окружность и вершина
пирамиды проектируется в
центр этой окружности.

16.

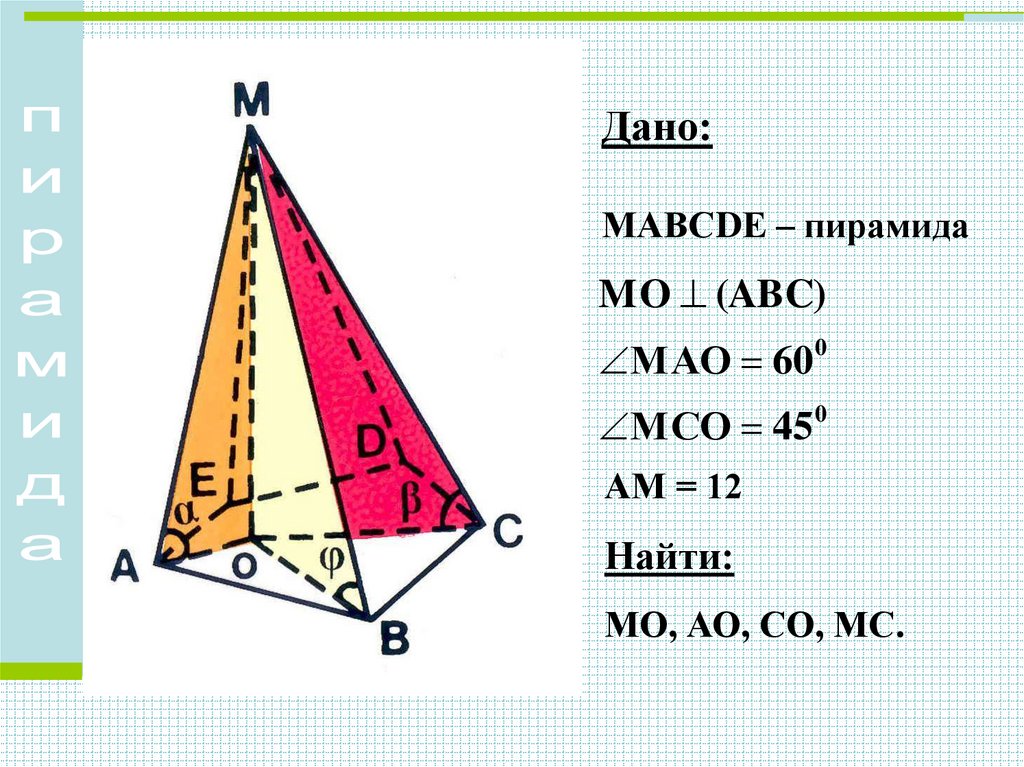
Дано:
МАВСDЕ – пирамида
MO (ABC)
МАО 60 0
МСО 45 0
АМ = 12
Найти:
МО, АО, СО, МС.

17.

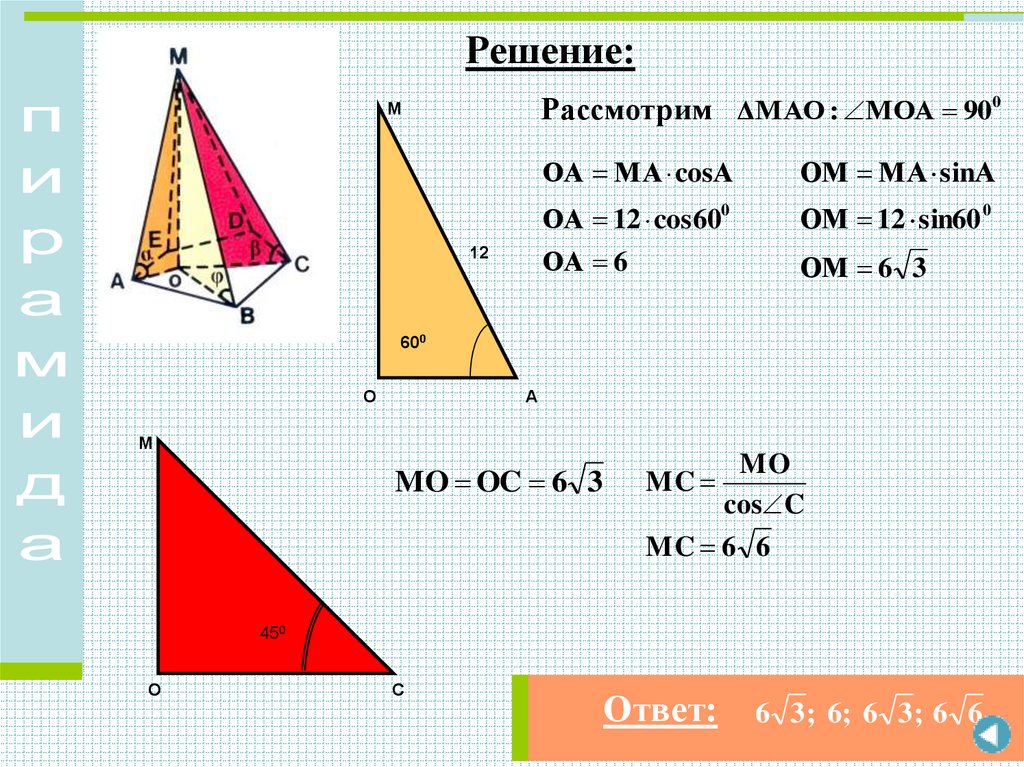
Решение:
Рассмотрим ΔMAO : МОА 900
М
12
ОА МА cosА
ОМ МА sinА
ОА 12 cos600
ОМ 12 sin60 0
ОА 6
ОМ 6 3
600
О
А
М
MO OC 6 3
MO
cos C
MC 6 6
MC
450
О
С
Ответ:
6 3 ; 6; 6 3 ; 6 6

18.

М
Аn
А1
О
А2
К
А3
А4
α

19.

СВОЙСТВО ПИРАМИДЫ
В четырехугольной пирамиде углы между
плоскостями основания и боковых граней
равны.
Докажите, что вершина пирамиды
проектируется в центр окружности, вписанной
в основание.

20.

В ы в о д:
Если в пирамиде все
двугранные углы при
ребрах основания
равны, то в основание
пирамиды можно
вписать окружность и
вершина пирамиды
проектируется в центр
этой окружности.

21.

Дано:
МАВСDN – пирамида
MO (ABC)
МЕО 30
0
МКО 45 0
МО 6
Найти: МК, ОК, МЕ, ОЕ

22.

Решение:
1. Рассмотрим ΔMOK : МОК 900
ОК МО 6
М
ОМ
МК
sinК
6
МК
6 2
0
sin45
6
О
450
К
2. Рассмотрим ΔMOE : МОЕ 900
МЕ = 2МО (свойство катета, лежащего против угла в 300)
МЕ = 12
ОЕ МО ctgЕ
М
ОЕ 6 ctg30 0
6
О
OE 6 3
300
Е
Ответ: 6 2 ; 6; 12; 6 3

23.

Формулы для нахождения площади боковой
поверхности, площади полной поверхности и
объема пирамиды.
Sб=S1+S2+S3+…+Sn
Sп=Sб+Sосн
1
V S осн H
3

24.

α
К
α

25.

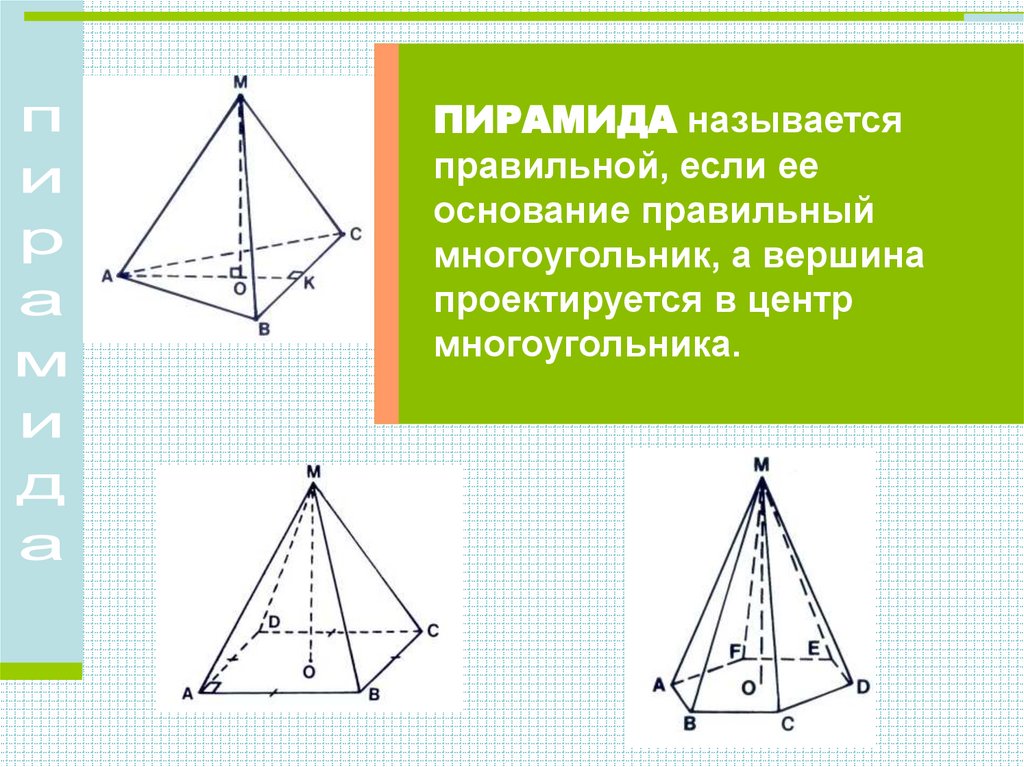
Виды пирамид

26.

ПИРАМИДА называется
правильной, если ее
основание правильный
многоугольник, а вершина
проектируется в центр
многоугольника.

27.

Итог урока:
Определение пирамиды
Элементы пирамиды
Правильные пирамиды

28.

Задача на слайде 7.3.
Дано:
МАВСДЕ – пирамида
АМ = 12
Найти: МО, АО, СО, МС
Решение
Рассмотрим
300
МС = 2МО (свойство катета, лежащего против угла в 300)
Ответ:
В боковых ребрах.
Вывод: Если в пирамиде все боковые ребра равны, то около основания пирамиды можно описать окружность и вершина пирамиды проектируется в центр этой окружности.
К углу наклона бокового ребра к плоскости основания.
Вывод: Если все ребра пирамиды одинаково наклонены к плоскости основания, то:
Около основания пирамиды можно описать окружность и вершина пирамиды проектируется в центр этой окружности.
Около такой пирамиды можно описать шар. Центр описанного шара лежит на прямой, содержащей высоту шара..
Задача со слайда 7.4
Л.С. Атанасян. п. 28, 29
«Учимся решать задачи»
Дано:
МАВСДN – пирамида
Найти: МК, ОК, МЕ, ОЕ
Решение
1. Рассмотрим М
стр. 27 задачи № 1, 2, 3. стр. 29 №1 (1-6); №3.
Рассмотрим 6
МЕ = 2МО (свойство катета, лежащего против угла в 300)
МЕ = 12
Ответ:
Диктант
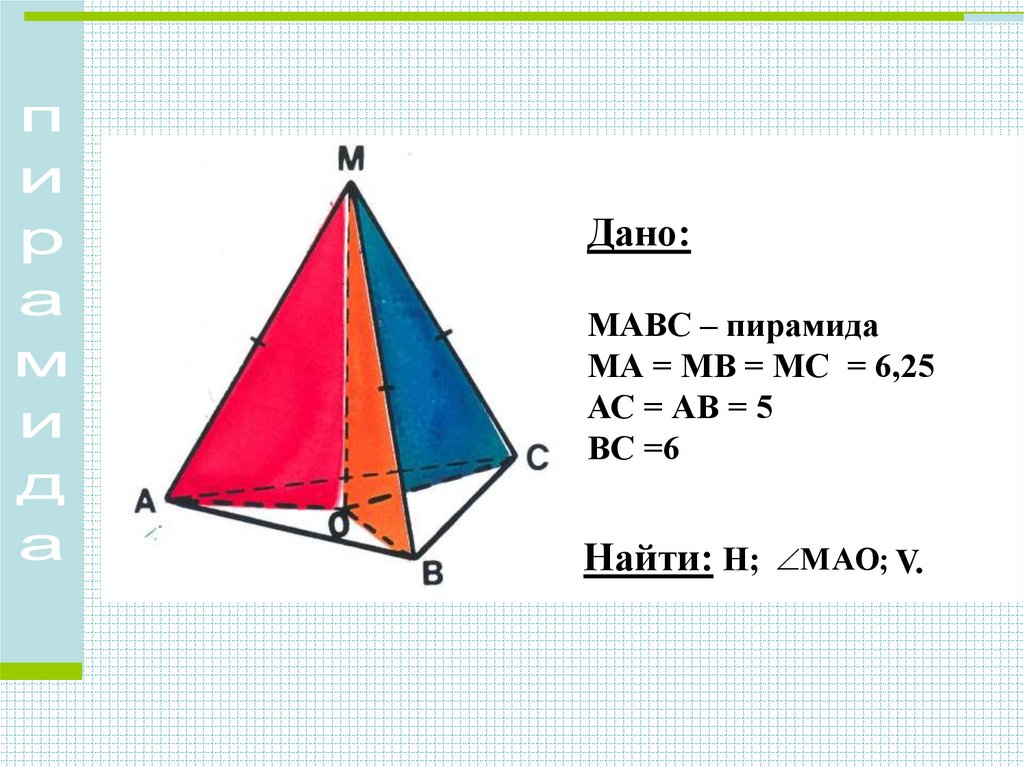
Дано:
МАВС – пирамида
МА = МВ = МС = 6,25
АС = АВ = 5
ВС =6
Найти: Н; V
Решение
Так как МА = МВ = МС, то ОА = ОВ = ОС = R
По формуле Герона
Итак,
Рассмотрим
По следствию из теоремы Пифагора ;
Рассмотрим
Ответ:
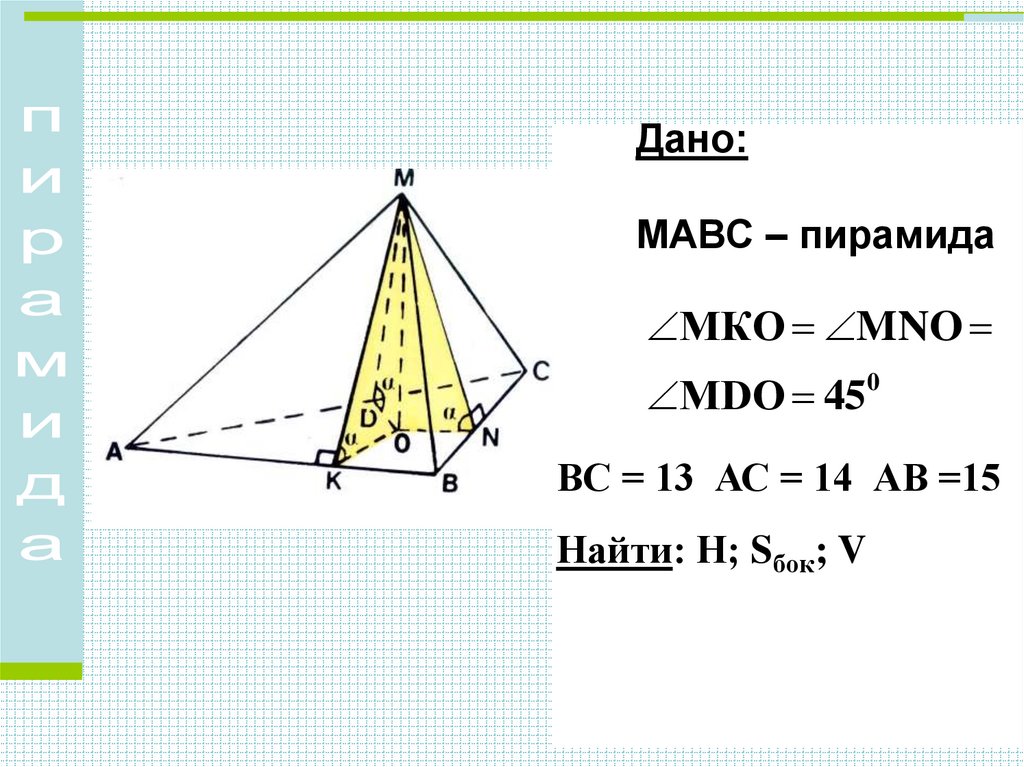
МАВС – пирамида
ВС = 13 АС = 14 АВ =15
Найти: Н; Sбок; V
боковых ребрах.
Вывод: Если в пирамиде все боковые ребра равны, то около основания пирамиды можно описать окружность и вершина пирамиды проектируется в центр этой окружности.
К углу наклона бокового ребра к плоскости основания.
Вывод: Если все ребра пирамиды одинаково наклонены к плоскости основания, то:
Около основания пирамиды можно описать окружность и вершина пирамиды проектируется в центр этой окружности.
Около такой пирамиды можно описать шар. Центр описанного шара лежит на прямой, содержащей высоту шара..
Задача со сл
2003

29.

Дано:
МАВС – пирамида
МА = МВ = МС = 6,25
АС = АВ = 5
ВС =6
Найти: Н;
МАО; V.

30.

Решение:
1. Так как МА = МВ = МС, то ОА = ОВ = ОС = R, R
По формуле Герона S p(p a)(р в)(р с) , где р
5 5 6
3,125.
Итак, R
4 12
авс
4S
а в с
.
2

31.

2. Рассмотрим
ΔAMO : МОА 900
По следствию из теоремы Пифагора
ОМ АМ 2 ОА 2
2
2
25 3
25 25
ОМ
8
4 8
3. Рассмотрим
ОА
cos МАО
.
АМ
ΔAMO : МОА 900
cos МАО 0,5. МАО 600
1
1
25 3 25 3
4. V S осн Н. V 12
3
3
8
2
Ответ:
25 3
25 3
; 600 ;
8
2

32.

Дано:
МАВС – пирамида
МКО MNO
МDО 45
0
ВС = 13 АС = 14 АВ =15
Найти: Н; Sбок; V

33.

Решение:
Так как МКО MNO МDО
ОК = r.
Рассмотрим
М
ΔMOK : МОК 900 ;
О
S
r
p
450
К
МКО 450
MO OK r
а в с
S p(p a)(p в)(p c) , где р
2
84
r
4
S 21 8 7 6 84
21
Итак, МО = ОК = 4

34.

S бок
S осн
84
S бок
84 2
0
cosα
cos45
1
V S осн H
3
1
V 84 4 112
3
Ответ: 4; 84 2 ; 112.