Похожие презентации:
Несобственные интегралы (лекция 7)
1. Лекция 7 Несобственные интегралы
12. Несобственные интегралы с бесконечными пределами интегрирования ( I рода)
• Пусть промежутком интегрирования является луч а ; ,а функция y=f(x) интегрируема на каждом конечном
отрезке [a,b].
Геометрически задача состоит в нахождении
площади под кривой.
y
y=f(x)
а
b
a
a
f ( x)dx
f ( x )dx blim
в
x
Возьмем точку в, найдем площадь криволинейной
трапеции через определенный интеграл и устремим в к .
2
3.
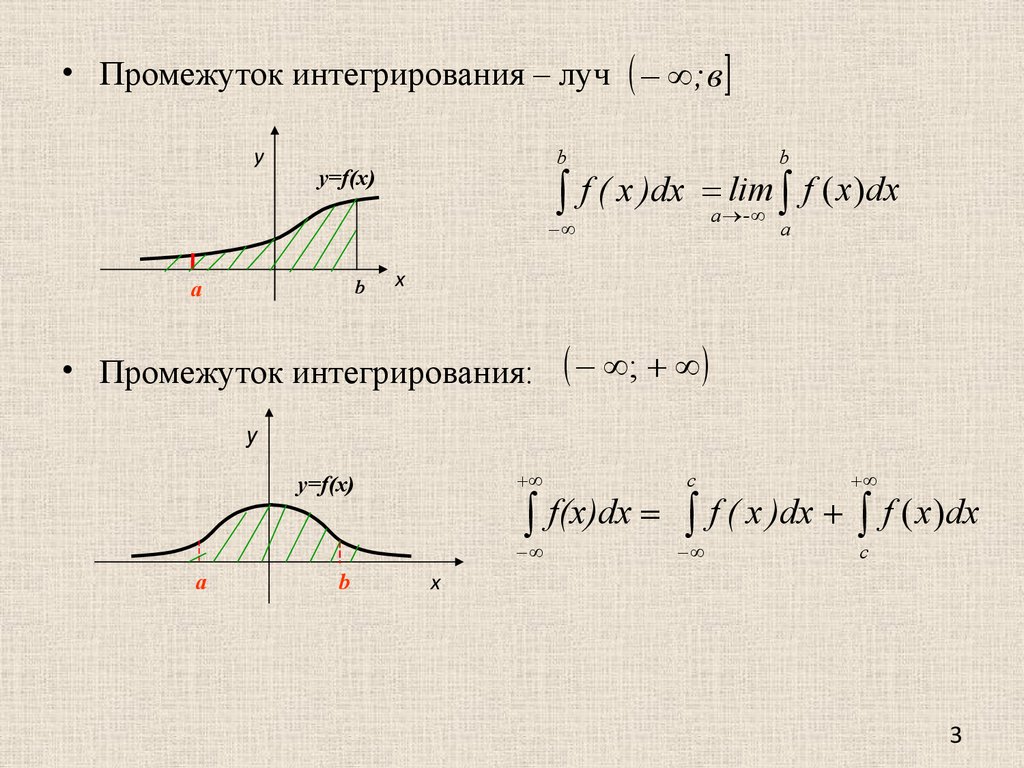
• Промежуток интегрирования – луч ; вy
b
b
f ( x )dx
y=f(x)
lim f ( x)dx
a -
b
a
a
x
• Промежуток интегрирования:
;
у
y=f(x)
a
b
c
c
f(x)dx f ( x )dx f ( x)dx
х
3
4.
Примеры1
b
b
dx
dx
lim lim ln x lim (ln b ln1 )
1 b
x b 1 x b
1
1
1
1
1 1
alim
1 1
x 2 dx alim
dx alim
x 2
a
x a
a
1
dx
1 x 2 arctg x 2 2
-
f ( x)dx F ( x)
F ( ) F ( )
4
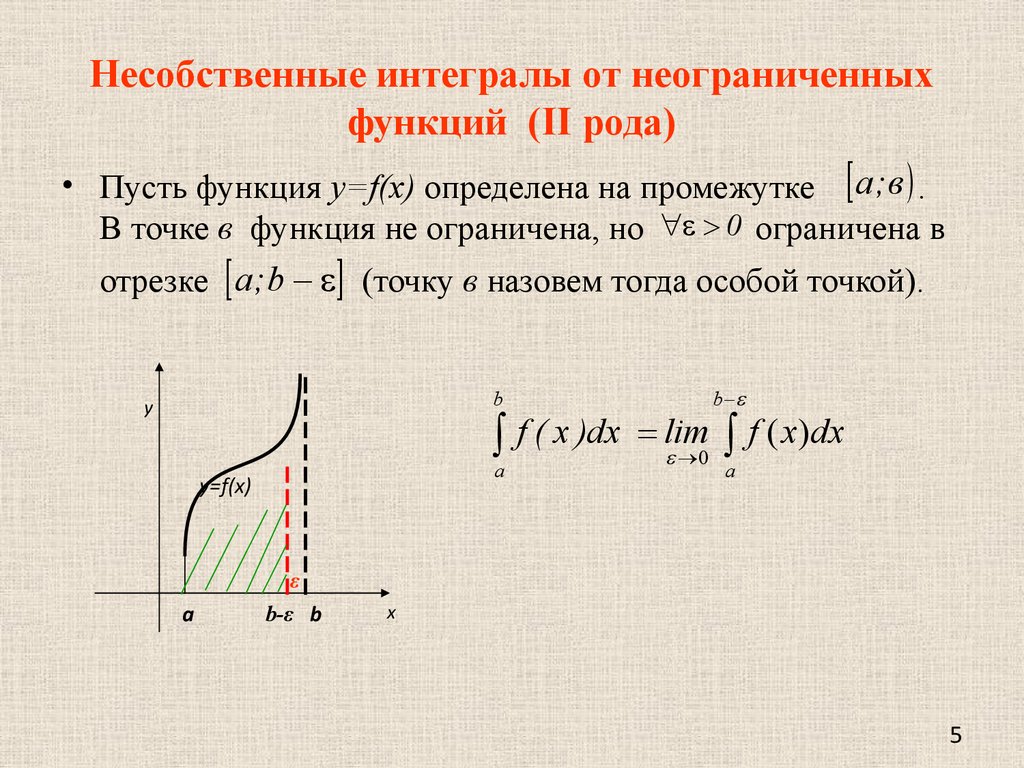
5. Несобственные интегралы от неограниченных функций (II рода)
• Пусть функция y=f(x) определена на промежутке а ; в .В точке в функция не ограничена, но 0 ограничена в
отрезке a ; b (точку в назовем тогда особой точкой).
b
y
f ( x )dx
a
y=f(x)
a
ε
b-ε b
lim
0
b
f ( x)dx
a
x
5
6.
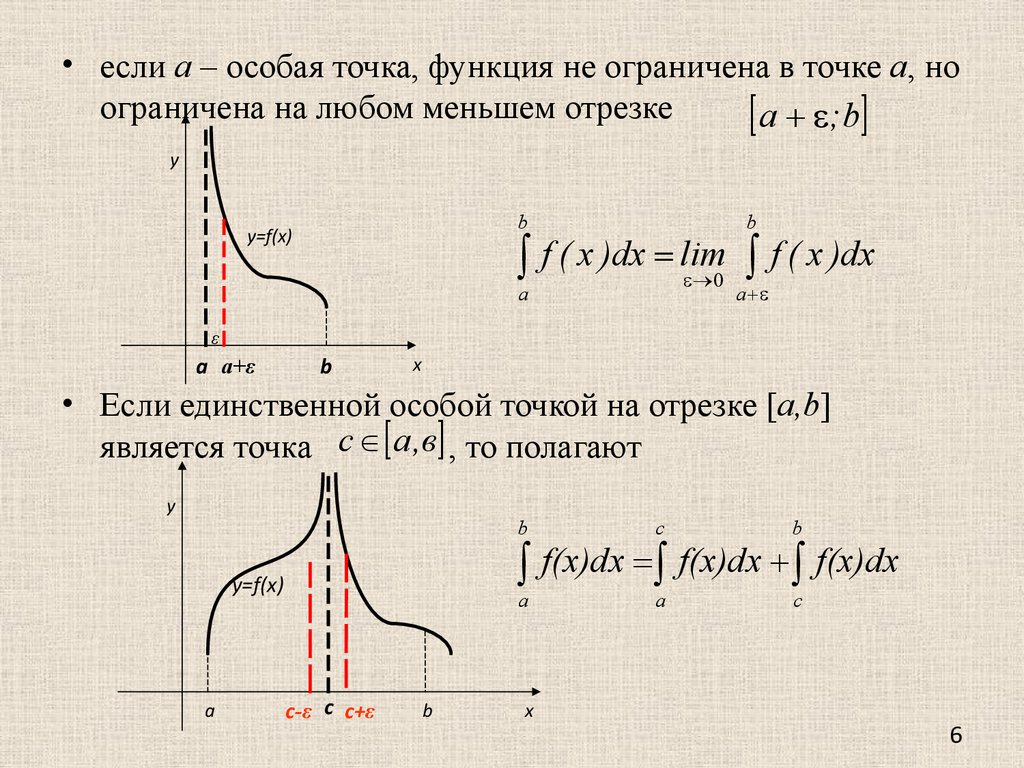
• если а – особая точка, функция не ограничена в точке а, ноограничена на любом меньшем отрезке
a ; b
y
y=f(x)
b
b
a
a
f ( x )dx
f ( x )dx lim
0
ε
a a+ε
b
x
• Если единственной особой точкой на отрезке [a,b]
является точка с а ,в , то полагают
y
c
b
a
a
c
f(x)dx f(x)dx f(x)dx
y=f(x)
a
b
с-ε с с+ε
b
x
6


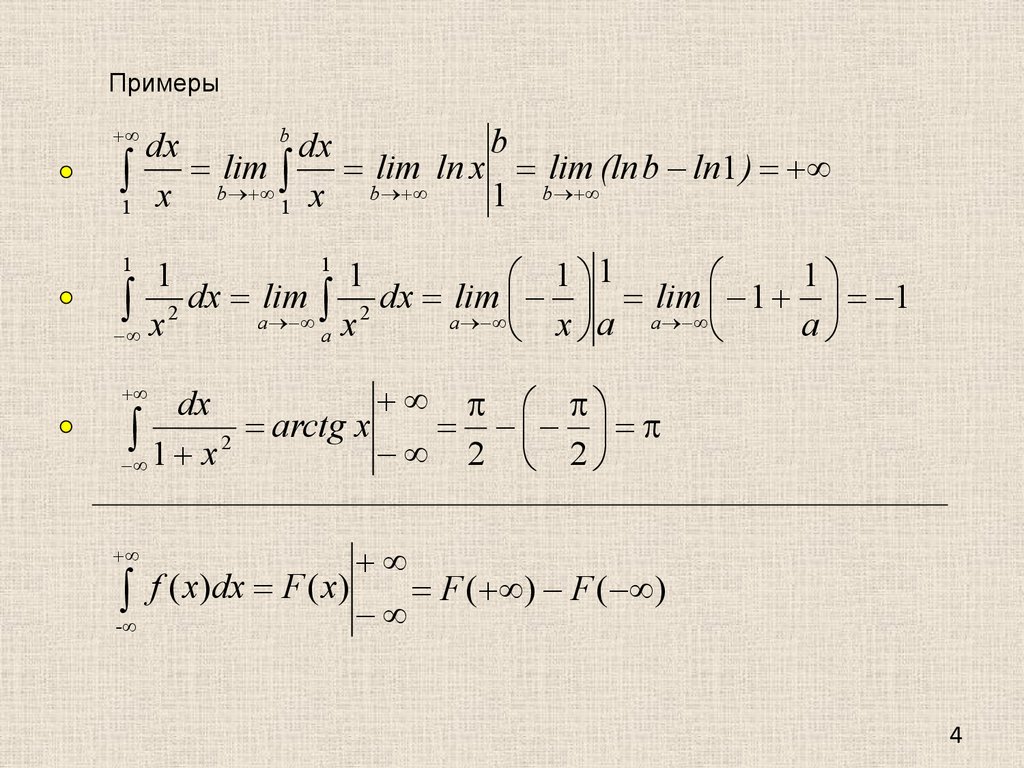
 Математика
Математика








