Несобственные интегралы. Лекция 6

1. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

Лекция 6

2. §1 Несобственные интегралы с бесконечными пределами интегрирования (I рода).

b
При определении определенного интеграла f x dx мы предполагали,
a
что:
1) отрезок интегрирования a, b конечный,
2) функция у f x непрерывна на отрезке a, b .
Если не выполняется хотя бы одно из этих условий, то интеграл
называется н е с о б с т в е н н ы м .
Пусть функция f x непрерывна на интервале a, . Тогда, если
существует (конечный или бесконечный) предел
b
lim f x dx ,
b
a
то его называют н е с о б с т в е н н ы м и н т е г р а л о м о т ф у н к ц и и
f x н а и н т е р в а л е a, и обозначают
f x dx .
a
b
Следовательно, по определению имеем f x dx lim f x dx .
a
b
a
(1.1)

3.

В случае, если этот предел к о н е ч е н , говорят, что интеграл (1.1)
с х о д и т с я , если же предел (1.1) б е с к о н е ч е н или вовсе н е
с у щ е с т в у е т , то говорят, что несобственный интеграл р а с х о д и т с я .
Аналогично определяются несобственные интегралы и для других
бесконечных интервалов:
b
b
f x dx alim
f x dx ,
a
c
f x dx f x dx f x dx ,
(1.2)
(1.3)
c
где с - любая фиксированная точка оси ОХ .
Несобственный интеграл
f x dx сходится тогда, когда сходится
каждый из несобственных интегралов в правой части равенства (1.3).

4.

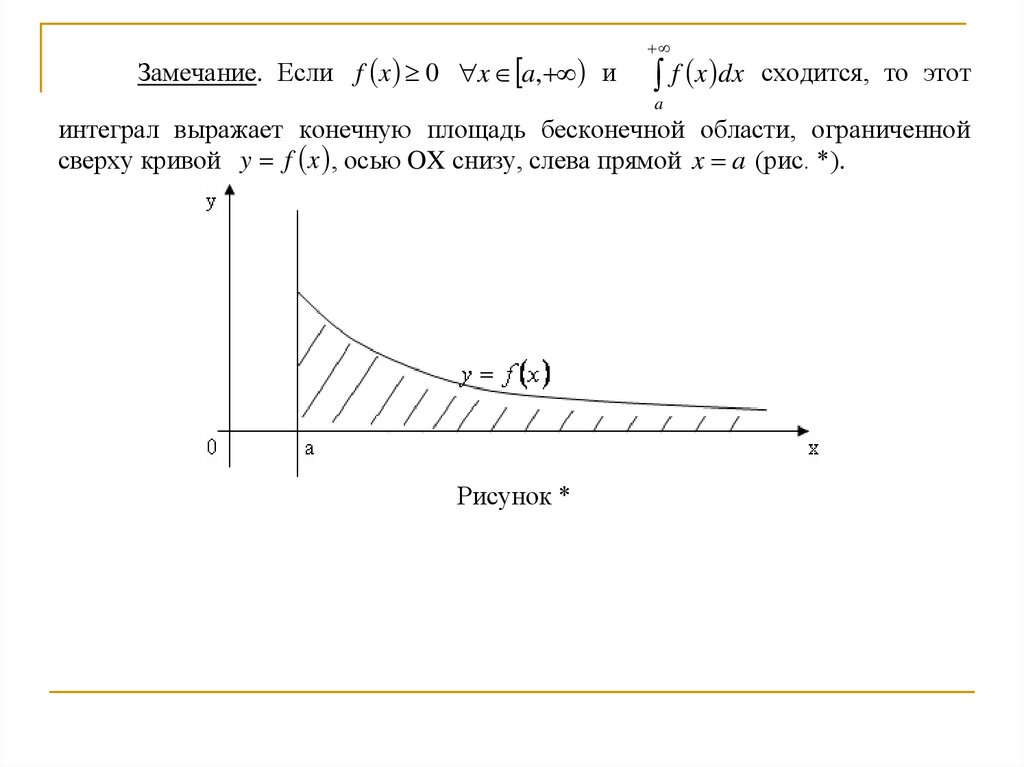
Замечание. Если f x 0 x a, и
f x dx сходится, то этот
a
интеграл выражает конечную площадь бесконечной области, ограниченной
сверху кривой y f x , осью OX снизу, слева прямой x a (рис. *).
Рисунок *

5.

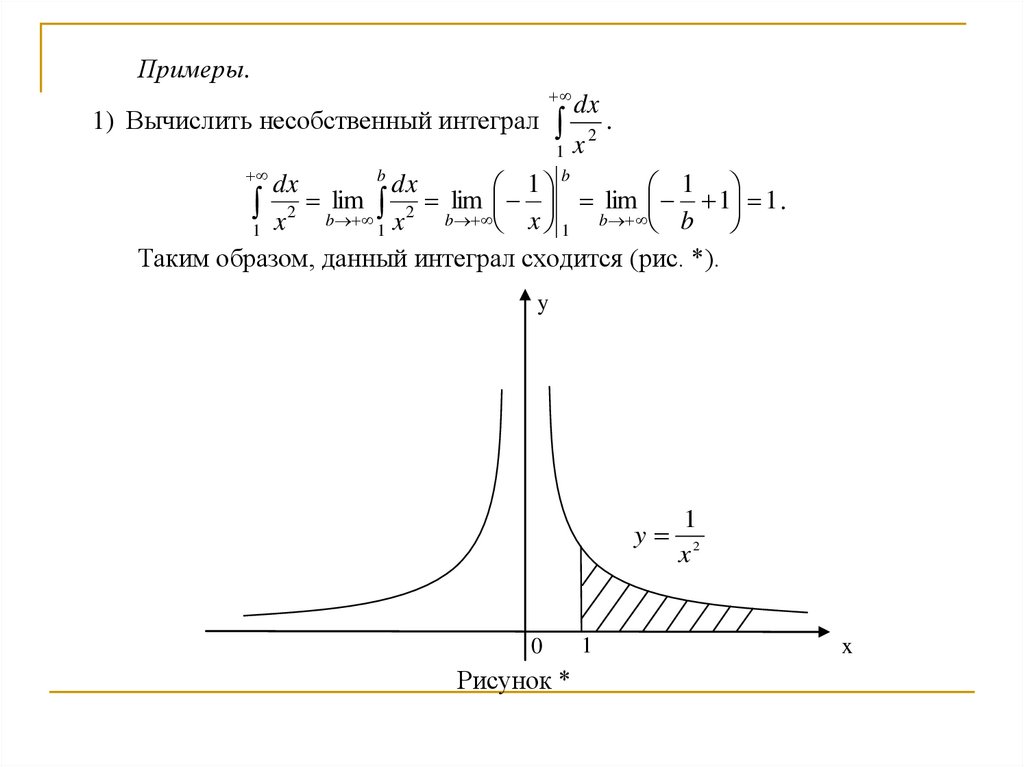
Примеры.
1) Вычислить несобственный интеграл
dx
1 x
b
2
.
b
dx
dx
1
1
lim
lim
lim
x 2 b x 2 b x b b 1 1 .
1
1
1
Таким образом, данный интеграл сходится (рис. *).
y
y
1
Рисунок * a
0
1
x2
x

6.

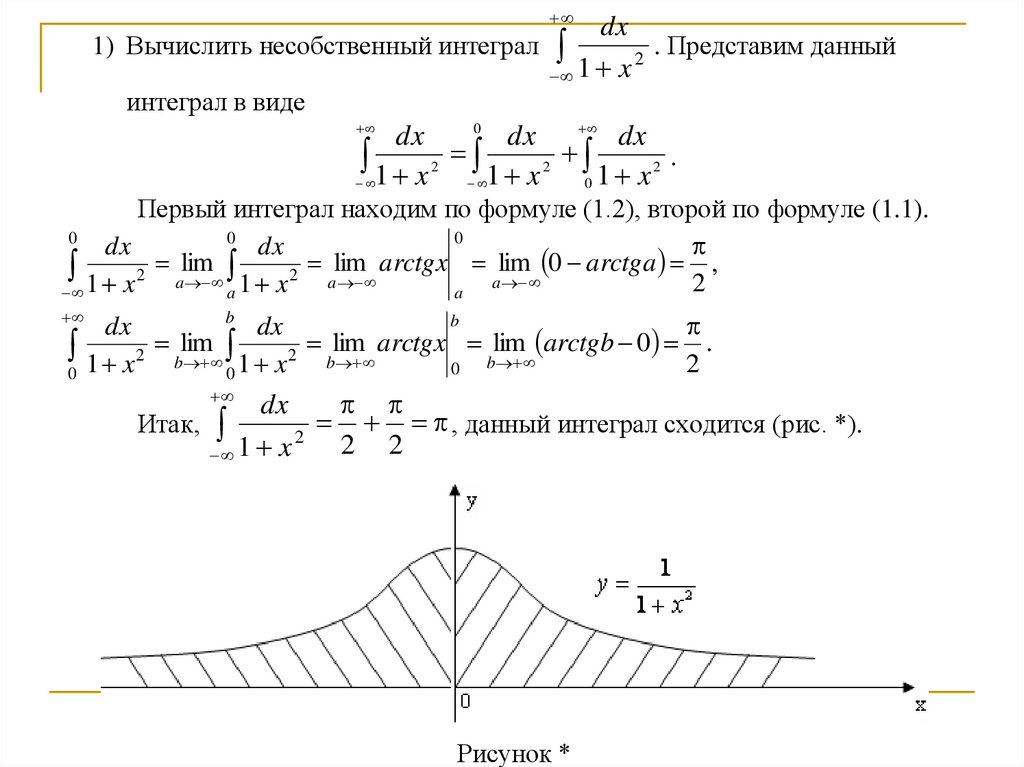
1) Вычислить несобственный интеграл
dx
1 x
2
. Представим данный
интеграл в виде
0
dx
dx dx
1 x 2 1 x 2 0 1 x 2 .
Первый интеграл находим по формуле (1.2), второй по формуле (1.1).
0
0
0
dx
dx
lim
lim
arctgx
lim
0
arctga
,
1 x 2 a 1 x 2 a
a
2
a
a
b
b
dx
dx
.
lim
lim
arctgx
lim
arctgb
0
1 x2 b 1 x2 b
b
2
0
0
0
dx
, данный интеграл сходится (рис. *).
Итак,
2
2 2
1 x
Рисунок *

7.

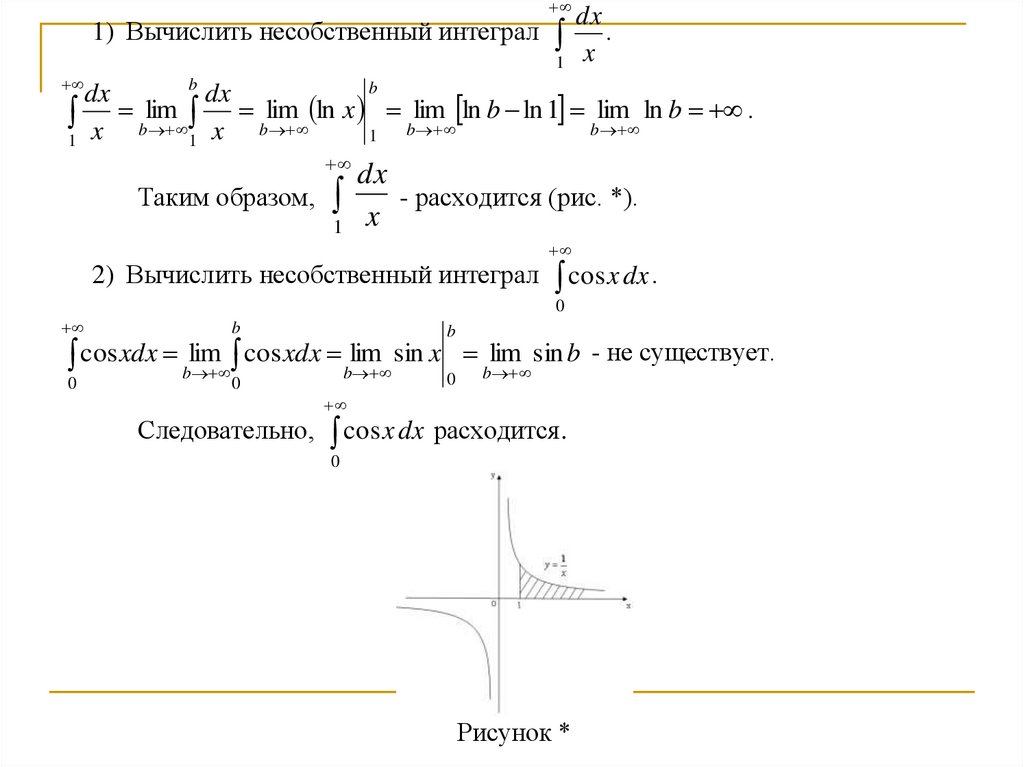
dx
.
1 x
1) Вычислить несобственный интеграл
b
b
dx
dx
lim ln x lim ln b ln 1 lim ln b .
x blim
x
b
b
b
1
1
1
dx
Таким образом,
- расходится (рис. *).
x
1
2) Вычислить несобственный интеграл cos x dx .
0
b
0
0
b
sin x lim sin b - не существует.
cos xdx blim
cos xdx blim
b
0
Следовательно, cos x dx расходится.
0
Рисунок *

8. §2 Признаки сходимости несобственных интегралов с бесконечными пределами интегрирования

Иногда бывает достаточно установить сходимость несобственного
интеграла, не вычисляя его значения. Для этого можно воспользоваться
следующими признаками сходимости.
Теорема 1 (признак сравнения). Пусть при x a выполняется неравенство
0 f ( x) ( x) . Тогда
a
a
1) если ( x) dx сходится, то сходится и интеграл f ( x) dx ;
2) если f ( x) dx расходится, то расходится и интеграл ( x) dx .
a
a
Примеры.
dx
.
3 x
1 x e
1) Исследовать сходимость интеграла
1
1
при x 1 .
3 x
3
xe
x
b
dx
x 2 b
1
1
1
3
сходится.
lim
x
dx
lim
lim
1
x3 b
b 2 1
b b 2
2
2
1
1
dx
dx
Поскольку 3 сходится, следовательно, 3 x сходится.
1 x
1 x e

9.

ln x
dx .
2) Исследовать сходимость интеграла 3
x
e
Так как ln x 1 при x e , то
ln x 1
3
x 3 x
или
3
1 ln x
.
x 3 x
2
1
2
3 b
2
dx
3
x
3
3 dx lim
3 e3
lim
x
lim
b
.
3
b
b 2 e
b
2
x
e
e
b
dx
ln x
Несобственный интеграл 3 расходится, тогда 3 dx расходится.
x
e x
e
Теорема 2. Пусть при x a верно неравенство f ( x) ( x) ( ( x) 0) . Тогда, если
( x) dx сходится, то сходится и интеграл f ( x) dx .
a
a
Несобственный интеграл f ( x) dx называется а б с о л ю т н о с х о д я щ и м с я , если
a
сходится f ( x) dx .
a
Несобственный интеграл f ( x) dx называется у с л о в н о с х о д я щ и м с я , если он
a
сходится, а f ( x) dx расходится.
a

10.

cos x
dx .
3
x
1
Пример. Исследовать на абсолютную сходимость
cos x
dx .
3
1 x
Составим
cos x
1
.
x3
x3
cos x
dx 1
dx сходится (по признаку сравнения).
Т.к. 3 сходится, то
3
x
2
1
1 x
cos x
Следовательно, 3 dx - абсолютно сходящийся.
1 x
Замечание. На практике иногда сходимость
устанавливают с помощью следующего признака.
Интеграл f ( x) dx (a>0):
a
M
и m 1;
xm
M
расходится, если f ( x) m и m 1 ,
x
где M , m const .
сходится, если f ( x)
несобственных
интегралов

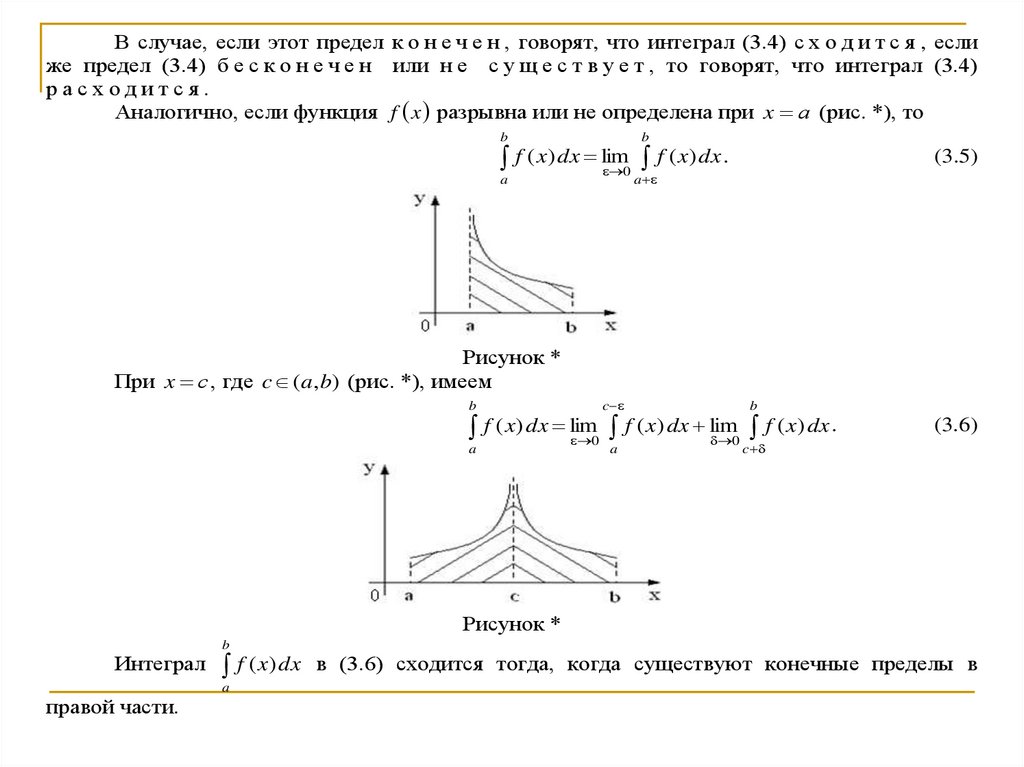
11. § 3 Несобственные интегралы от неограниченных функций (II рода)

Пусть функция f x определена и непрерывна на интервале a, b , а
при x b либо не определена, либо имеет разрыв (рис. *). Тогда, если
b
существует (конечный или бесконечный) предел lim f ( x) dx , то его
0
a
называют н е с о б с т в е н н ы м и н т е г р а л о м о т н е о г р а н и ч е н н о й
b
ф у н к ц и и f x и обозначают f ( x) dx .
a
Следовательно, по определению имеем
b
b
f ( x) dx lim
f ( x) dx .
0
a
a
Рисунок *
(3.4)

12.

В случае, если этот предел к о н е ч е н , говорят, что интеграл (3.4) с х о д и т с я , если
же предел (3.4) б е с к о н е ч е н или н е с у щ е с т в у е т , то говорят, что интеграл (3.4)
расходится.
Аналогично, если функция f x разрывна или не определена при x а (рис. *), то
b
b
f ( x) dx lim f ( x) dx .
0
a
(3.5)
a
Рисунок *
При x с , где c (a, b) (рис. *), имеем
c
b
b
f ( x) dx lim f ( x) dx lim f ( x) dx .
a
0
a
0
(3.6)
c
Рисунок *
b
Интеграл
f ( x) dx в (3.6) сходится тогда, когда существуют конечные пределы в
a
правой части.

13.

Примеры.
1
1
1
dx
dx
lim
lim 2 x 2 lim (1 ) 2 , интеграл сходится.
1)
0
0
0
0 x
x
1
2)
1
dx
1 x
0
2
lim
0
0
dx
1 x
2
lim (arcsin x)
lim arcsin(1 ) arcsin 0
0
0
1
0
, интеграл сходится.
2
1
2
x 1
dx
dx
dx
x 1 беск . разрыв x 1 x 1 .
1
1
1
2
3)
1
dx
lim
lim ln x 1 lim ln ln 2 .
0
0
0
1 x 1
1
1
1
2
dx
dx
Так как
расходится, следовательно,
расходится.
x
1
x
1
1
1

14. §4 Признаки сходимости несобственных интегралов от неограниченных функций.

Теорема 3. Пусть при x a, b выполнено неравенство 0 f ( x) ( x) и при
x b функции f (x) и (x) либо не определены, либо имеют разрыв. Тогда
b
1) если ( x) dx сходится, то
a
b
b
f ( x) dx сходится.
a
2) если f ( x) dx расходится, то
b
( x) dx расходится.
a
a
Теорема 4. Пусть при x a, b выполнено неравенство f ( x) ( x) ,
( x) 0 , а функции f (x ) и ( x ) либо не определены, либо имеют разрыв
b
b
a
a
при x b . Тогда если ( x) dx сходится, то и f ( x) dx сходится.
Замечание. Если f (x) имеет бесконечный разрыв в одном из концов
интервала а, b , например, в точке x а , то несобственный интеграл
b
f ( x) dx : 1) сходится, если
M
и m 1;
m
x a
M
f ( x)
и m 1.
m
x a
f ( x)
a
2) расходится, если

15.

80
1
Пример. Исследовать на сходимость
0
x dx
1 x
4
.
Очевидно, что
x
1 x4
1
, x 0,1 .
1 x
1
0
1
dx
2
lim (1 x) dx lim 2 1 x 2 lim (1 ) 2 .
0 0
0
0
0 1 x
1
1
1
dx
x dx
Тогда
сходится, следовательно, интеграл
тоже сходится.
4
1
x
0 1 x
0
1