Похожие презентации:
Моделирование распространения фотонов с помощью метода Монте-Карло
1.
окончательно1
Ω Σ (r , E ) Σ t (r , E ) f (r ; Ω , E Ω, E ) d dE Q(r , Ω, E , t )
v t
Методы решения:
1. PIJ приближение – метод ВПС (вероятности первых столкновений)
2. Pn приближение
Разложение Ф, Q и
f (r ; Ω , E Ω, E )
в ряд по полиномам Лежандра
3. Sn приближение (метод дискретных ординат)
f (r ; Ω , E Ω, E ) d wm (r , Ωm )
4. Метод Монте-Карло
m
2.
dnD - a Q
d
3.
v n1 d
D - a Q
v d
4. Пусть
d0
dτ
Тогда
D a
Q
5. Уравнение условно-критического реактора
1D a Q
k
k – эффективный коэффициент размножения
k
Qdv
D dv adv
6. Замедление нейтронов при рассеянии
Ei-1Ei
Ei+1
Ej
E
7.
Q = Qm + Qj i + Q S0источник мгновенных нейтронов
Qm - деления;
Qj i -источник нейтронов за счет замедления из других групп в
данную;
Q источник запаздывающих нейтронов;
источник “внешних” нейтронов, т.е. нейтроны этого источника
не 0
обусловлены цепной реакцией деления протекающей в ядерном реак
S -
Qm Q f
Qj i = s Pj i ; j i s Pj i
a a s P i j;
a a d
s P i j d
8.
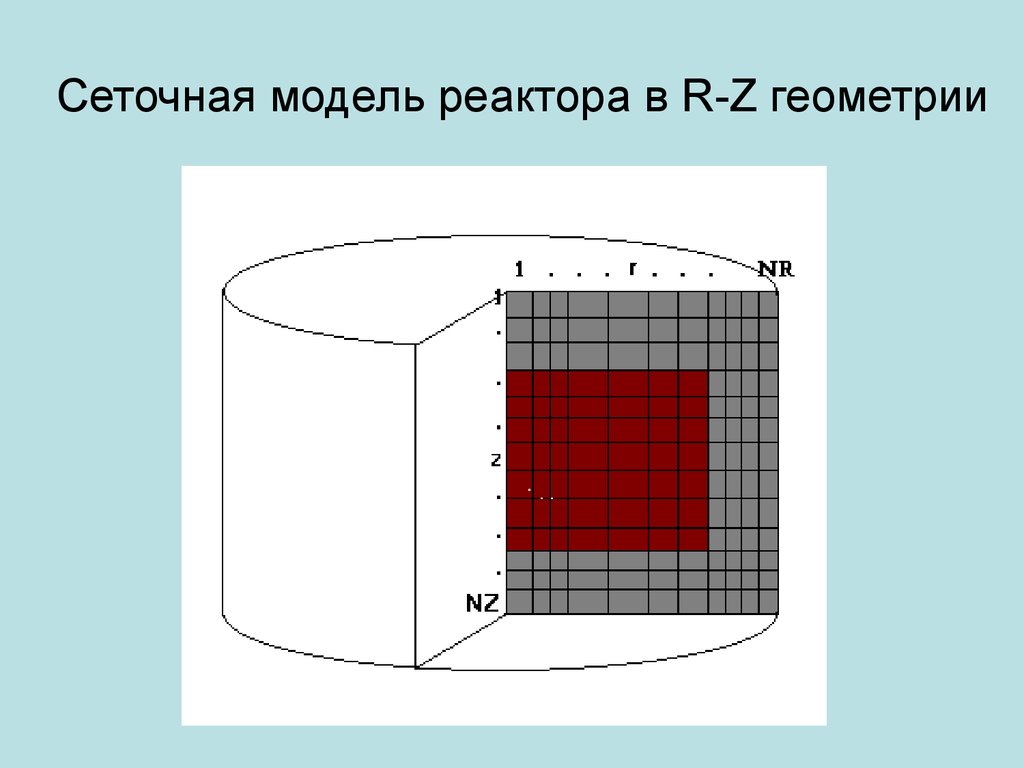
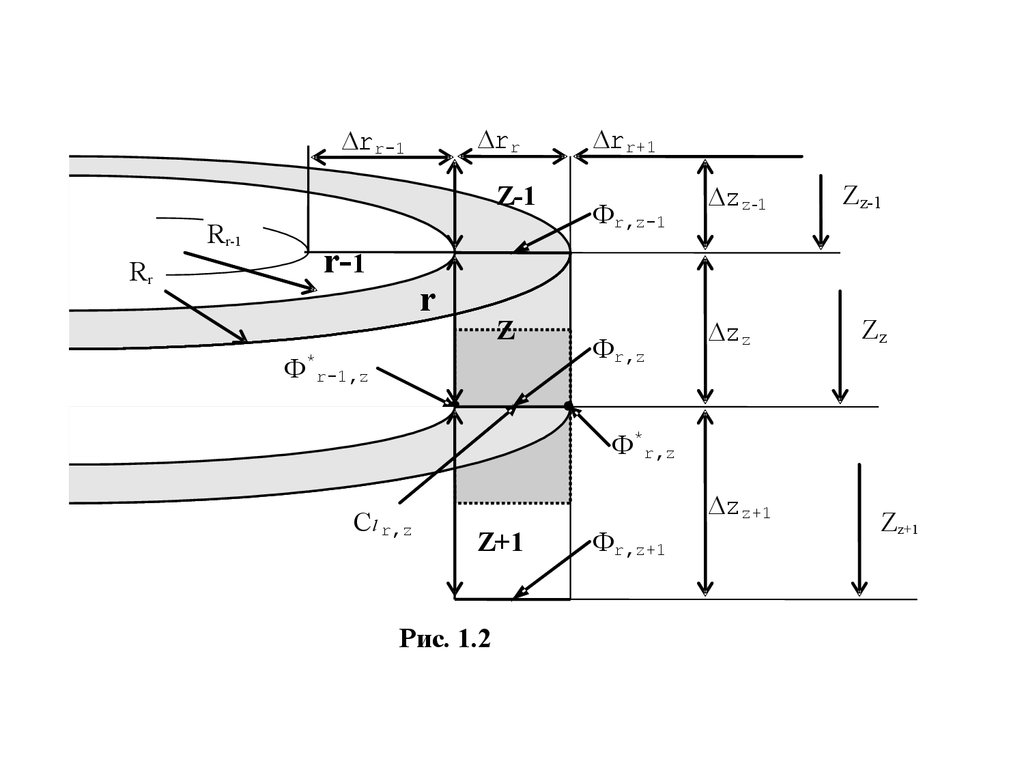
9. Сеточная модель реактора в R-Z геометрии
10.
rrrr-1
Z-1
Rr-1
Rr
r-1
r
Z
Ф*r-1,z
rr+1
Фr,z-1
Фr,z
zz-1
zz
Zz-1
Zz
Ф*r,z
Cl r,z
zz+1
Z+1
Рис. 1.2
Фr,z+1
Zz+1
11.
NEZz
Zz + 1
Qi (r )dv = i j fj, r, z
j fj, r, z + 1
j, r, z Sr
2
2
j =1
V*rz
k i
k i
k, r, z Zz
k, r, z + 1 Zz + 1
k, r, z Sr S 0 i , r, z Zz S 0 i, r, z + 1 Zz + 1 Sr
2
2
2
2
k = i +1
NE
ai , r, z + di , r, z Zz ai , r, z + 1 + di , r, z + 1 Zz + 1
ai (r ) + di (r ) i (r )dv =
i, r, z Sr
V*rz
2
2
12.
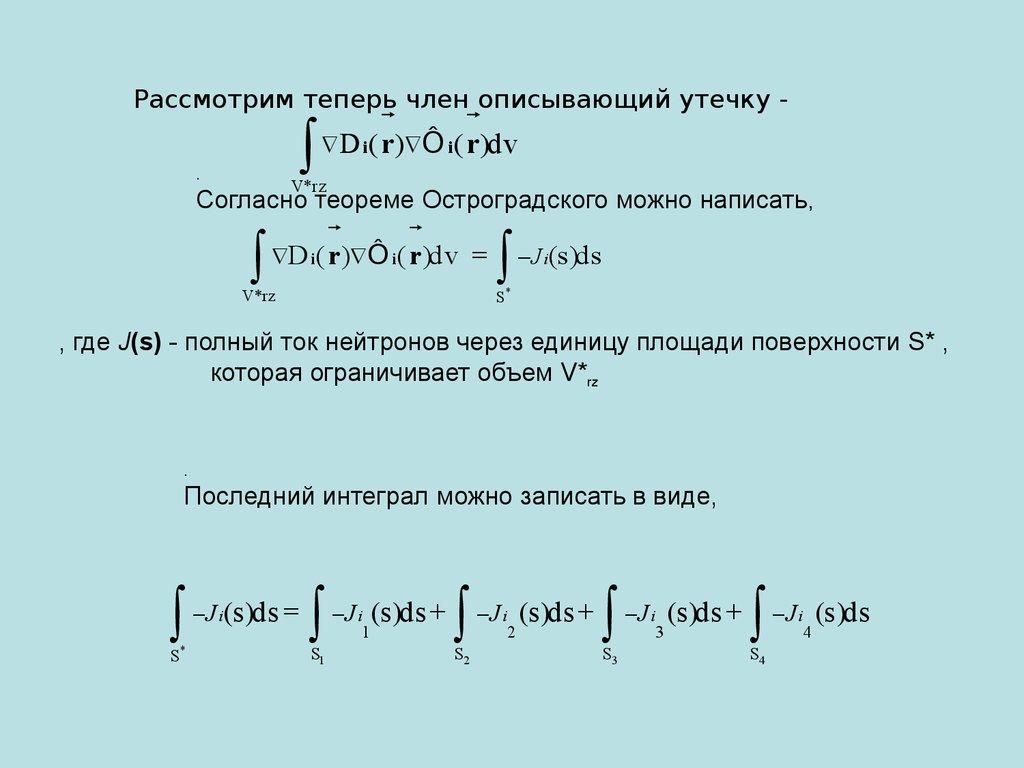
Рассмотрим теперь член описывающий утечку -.
D i( r ) Ô i( r )dv
V*rz
Согласно теореме Остроградского можно написать,
D i( r ) Ô i( r )dv =
J (s)ds
i
S*
V*rz
, где J(s) - полный ток нейтронов через единицу площади поверхности S* ,
которая ограничивает объем V*rz
.
Последний интеграл можно записать в виде,
J (s)ds = J (s)ds + J
i
S*
i
1
S1
S2
i
2
(s )ds +
J
S3
i
3
(s )ds +
J
S4
i
4
(s )ds
13.
Конечно-разностная аппроксимация указанных выше интегралов будетS1
i,r,z-1 - i,r,z
Ji (s)ds = Di, r, z
Sr
1
Z z
Ji (s)ds = Di, r, z + 1
3
S3
S2
i,r,z+1 - i,r,z
Sr
Z z +1
Zz + Zz + 1
* i, r, z - i, r, z
Ji (s)ds = Di, r, z
2 Rr (
)
2
rr
2
2
S4
i,* r -1,z - i,* r, z
Zz + Zz + 1
Ji (s)ds = Di, r, z
2 Rr - rr (
)
4
rr
2
2
14.
оток нейтронов на границе* i, r, z
определяется исходя из условия равенства токов нейтронов на данной гр
i, r, z - * i, r, z
*i, r, z - i, r + 1, z
Di, r, z
Di, r + 1, z
rr
rr + 1
2
Отсюда,
* i, r, z =
2
Di, r, z rr + 1 i, r, z + Di, r + 1, z rr i, r + 1, z
Di, r, z rr + 1 + Di, r + 1, z rr
*i, r - 1, z =
Di, r - 1, z rr + 1 i, r - 1, z + Di, r + 1, z rr - 1 i, r, z
Di, r-! , z rr + Di, r, z rr - 1
.
Подставляя получим,
Ji (s)ds =
J i
2
S2
S4
4
(s)ds=
Zz + Zz + 1
2 Di, r + 1, z Di, r, z
( i, r, z - i, r + 1, z ) 2 Rr (
)
Di, r, z rr + 1 + Di, r + 1, z rr
2
2 Di, r, z Di, r - 1, z
Zz + Zz + 1
( ô i,r,z - ô i,r - 1,z) 2 Rr - rr (
)
Di, r - 1, z rr + Di, r, z rr - 1
2
15. Граничные условия
ФNR,z=0,Фr,0=0,
Фr,NZ=0,
z=1,….,NZ
r=1,….,NR
r=1,….,NR
Нормировка потока нейтронов
NE NR NZ
W af f i, r, z i, r, z Vr, z
i 1 r 1 z 1
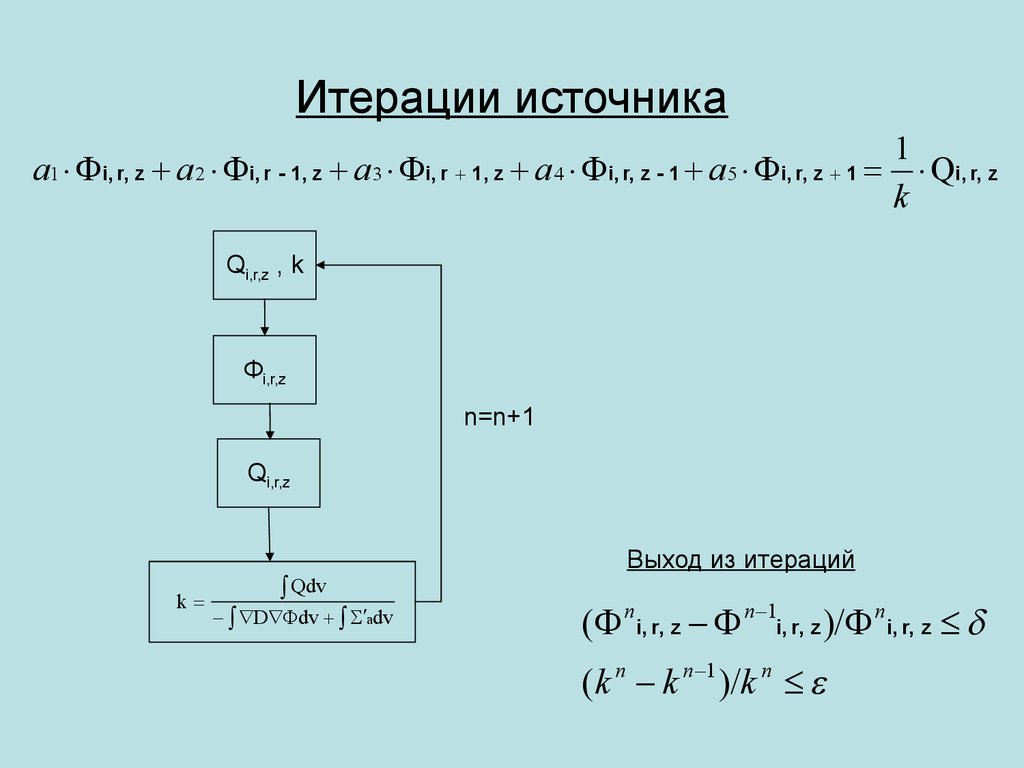
16. Итерации источника
1a1 i, r, z a 2 i, r - 1, z a 3 i, r 1, z a 4 i, r, z - 1 a 5 i, r, z 1 Qi, r, z
k
Qi,r,z , k
Фi,r,z
n=n+1
Qi,r,z
k
Qdv
D dv adv
Выход из итераций
( n i, r, z n 1i, r, z )/ ni, r, z
(k n k n 1 )/k n

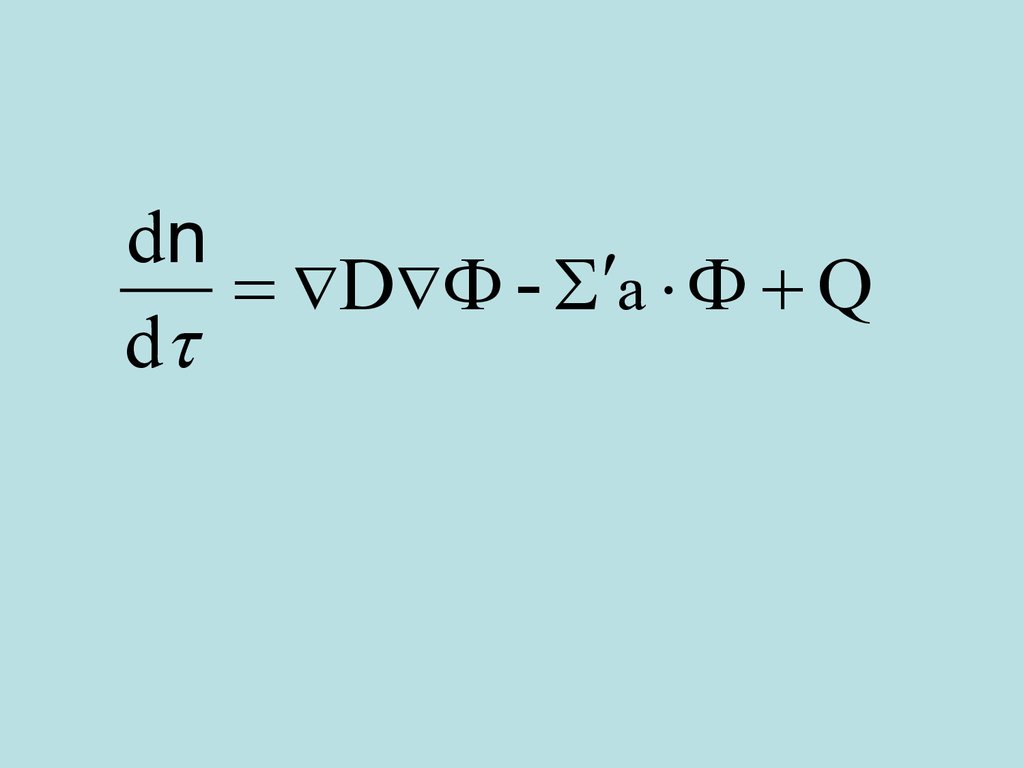

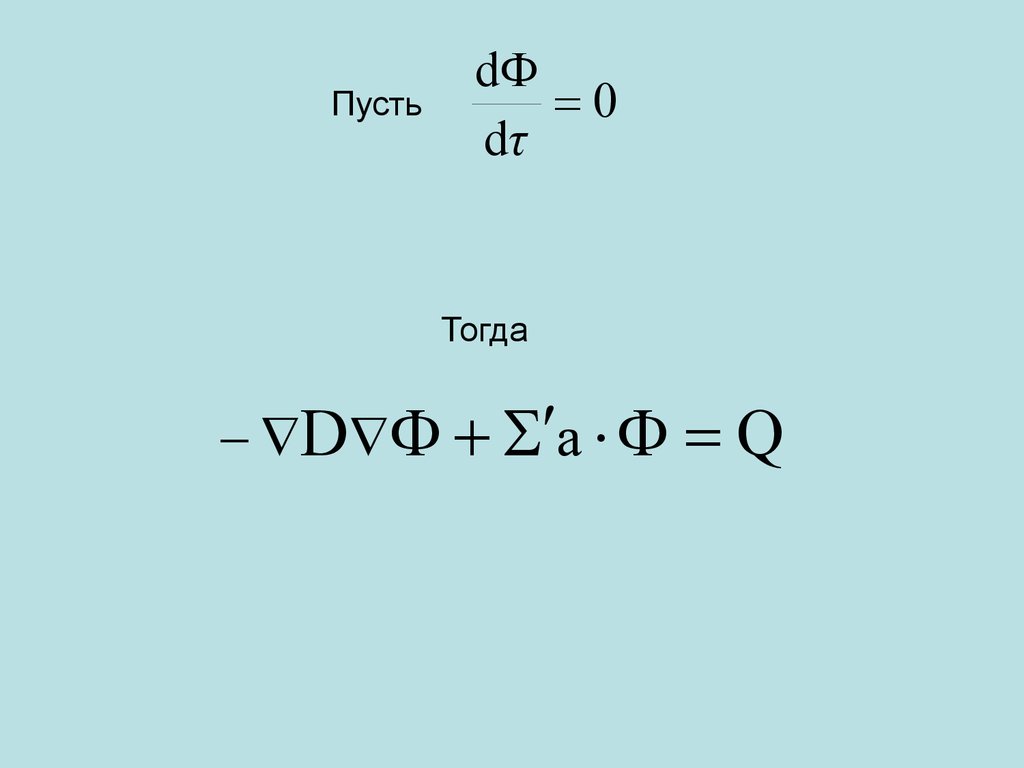







 Физика
Физика








