Похожие презентации:
Расчет констант равновесия статистическим методом. Лекция 23
1.
Лекция 23Расчет констант равновесия статистическим
методом.
Закон равнораспределения.
Расчет конфигурационного интеграла для
реального газа.
Закон соответственных состояний.
2.
Лекция 22Теории теплоемкости Эйнштейна и Дебая (без
вывода).
Вращательная и ядерная сумма по состояниям.
3.
Средняя кинетическая энергия и средняя скоростьмолекул в идеальном газе.
Найдите верные утверждения!
Значительная доля молекул имеет энергию выше средней
1.
2.
3.
4.
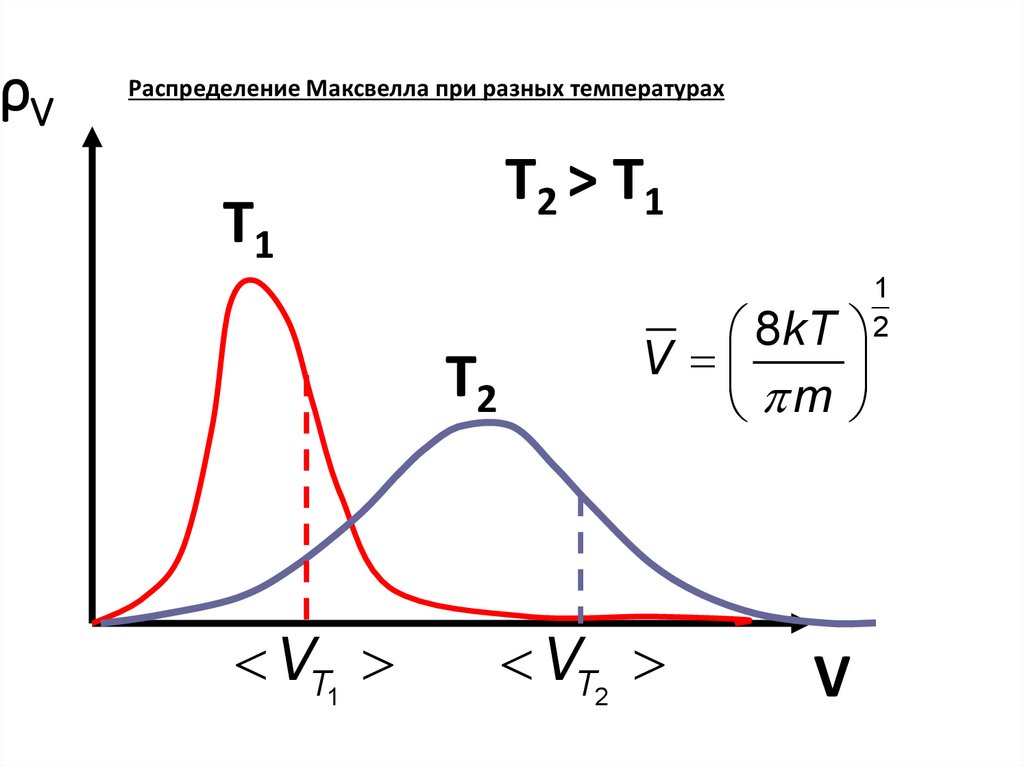
Средняя скорость растет с увеличением массы
Средняя энергия растет с увеличением массы
ср
m V
2
2
1 балла
4.
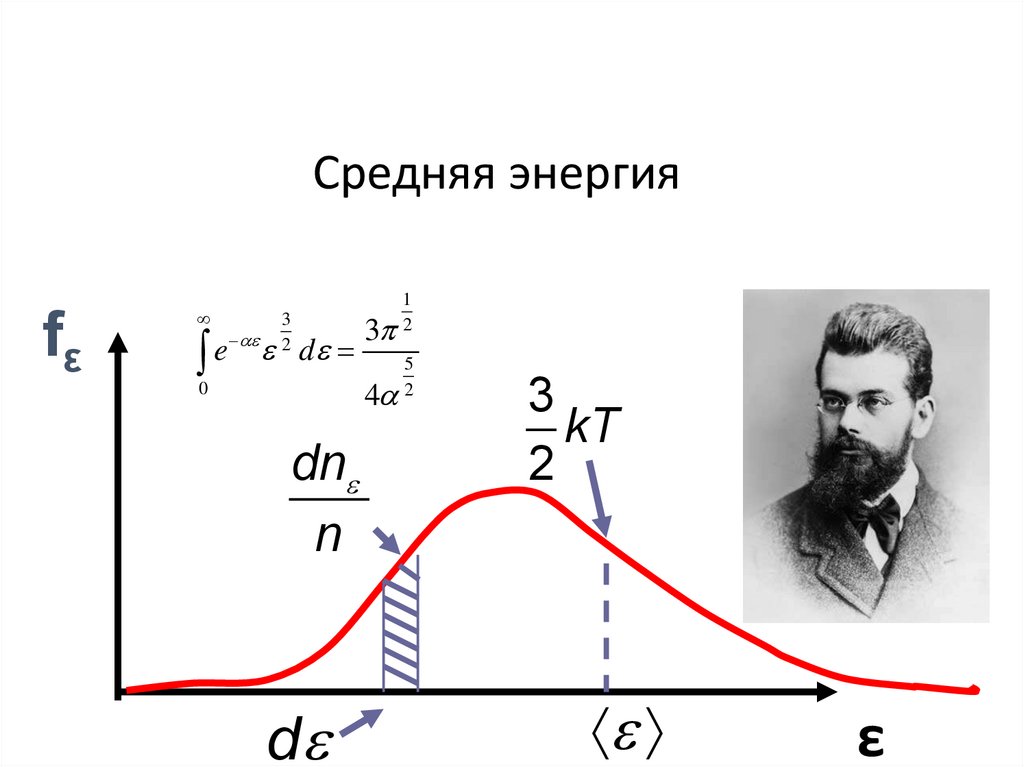
Средняя энергияfε
e
3
2
d
3
4
0
dn
n
d
1
2
5
2
3
kT
2
ε
5.
ρVРаспределение Максвелла при разных температурах
T2 > T1
T1
T2
VT1
8kT
V
m
VT2
V
1
2
6.
m V2
2
2
8kT
m
m
4
3
kT ср kT
2
2
1/2
mV 2 m 2
ср
V
2
2
V
V V dV ;
dV 2 2VdV
V2
2
2
V
dV
V2
7.
Для расчета суммы по состояниям Q существуют формулы (1) и (2)Q e
kТ
dpdq (1),
Q zi e
i
kT
(2)
i
которой из них нужно пользоваться?
1 балла
1. нужно воспользоваться формулой (1)
2. можно воспользоваться формулой (2), но лучше –
формулой (1)
3. иногда верна формула (1), а иногда – формула (2)
4. формула (2) верна всегда, а формула (1) – только в
особых случаях
8.
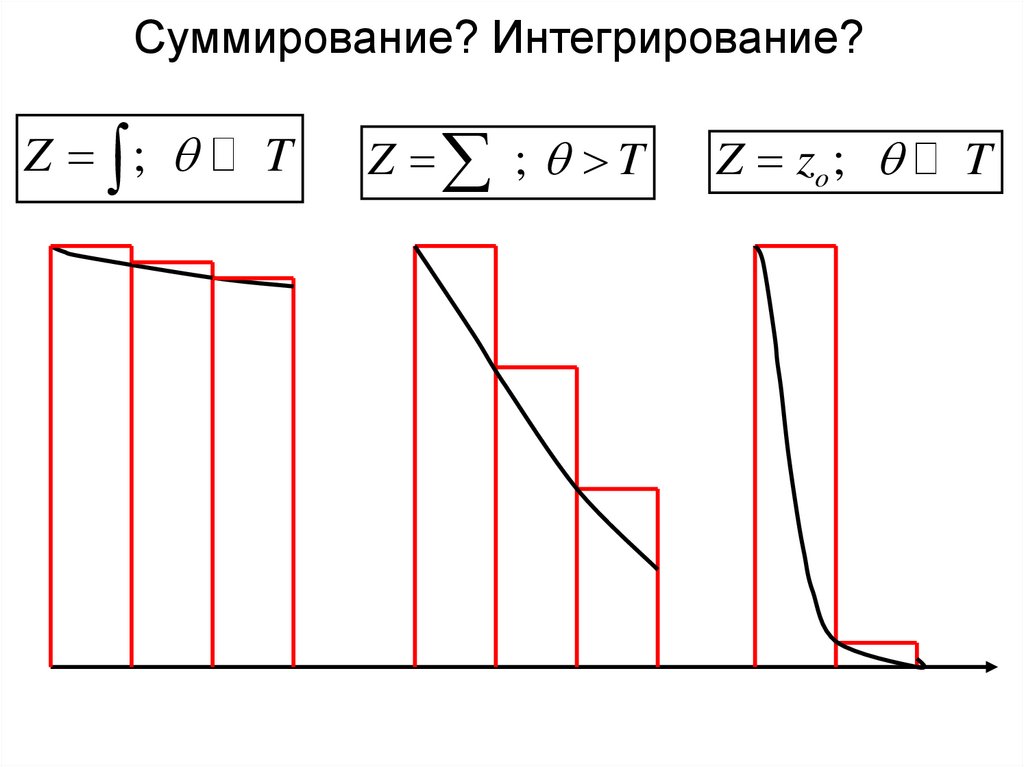
Суммирование? Интегрирование?Z ;
T
Z ; T
Z zo ;
T
9.
Чем мембранное равновесие отличается от фазового?Найдите верные утверждения!
2 балла
При мембранном равновесии :
1. Не во всех фазах температура одинакова.
2. Не во всех фазах давление одинаково.
3. Не во всех фазах энтропия смешения одинакова.
4. Не во всех фазах работает уравнение
Менделеева Клапейрона.
5. Не во всех фазах работает уравнение Гиббса Дюгема
10.
Какая из формул неверна для системы «идеальный газ»?1 балла
1. F E0 kT ln Z
2. F E0 RT ln Q
ln Z
2 ln Z
3. сV 2kT
kT
2
T V
T V
2
ln Q
2 ln Q
4. сV 2 RT
RT
2
T V
T V
2
11.
Максимальная теплоемкость СV идеального газа СО равна:3
1. R
2
5
2. R
2
3. 3R
7
4. R
2
1 балла
12.
ВРАЩАТЕЛЬНАЯ ТЕПЛОЕМКОСТЬ ДВУХАТОМНОГО ИДЕАЛЬНОГО ГАЗА.НАЙДИТЕ ПРАВИЛЬНОЕ УТВЕРЖДЕНИЕ
1. РАВНА R
1 балла
2. МОЖЕТ БЫТЬ БОЛЬШЕ R ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
3. МОЖЕТ БЫТЬ БОЛЬШЕ R ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
4. МОЖЕТ БЫТЬ БОЛЬШЕ R ЗА СЧЕТ ВНУТРЕННЕГО ВРАЩЕНИЯ
5. МОЖЕТ БЫТЬ БОЛЬШЕ R у ГОМОЯДЕРНОЙ МОЛЕКУЛЫ
13.
Ниже приводятся несколько утверждений относительноправила фаз Гиббса. Выберите из них правильные.
а) Правильного утверждения здесь нет!
2 балла
б) При выводе правила фаз используется уравнение Клаузиуса-Клапейрона;
в) Правило фаз описывает движение системы к термодинамическому равновесию
г) Правило фаз показывает, что в пятикомпонентной системе максимальное число фаз в
равновесии при постоянном давлении - 7;
д) Правило фаз показывает, что в трехкомпонентной системе максимальное число фаз в
равновесии - 4;
е) Правило фаз утверждает, что с = к+2-ф, где с - число степеней свободы, к-число
компонентов, ф- количество уравнений Гиббса-Дюгема, которые можно записать в
системе.
14.
СТАТИСТИЧЕСКИЙ РАСЧЕТТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ
ИДЕАЛЬНОГО ГАЗА
15.
Расчет термодинамических функцийZ;
Qe
ln Z N ln
;
N
QN
Z
N!
ln Z
ln Q
N
;
T
T
V
V
F E0 kT ln Z RT ln
2 ln Z
2 ln Q
N
2
2
T
V
T V
Qe
N
Qe
F
ln Z
ln Q
S
k
ln
Z
kT
R
ln
RT
N
T V
T V
T V
ln Z
2 ln Q
U E0 F E0 TS kT 2
RT
T V
T V
G E0 F E0 pV kT ln Z RT RT ln
Qe
Q
RT ln e RT ln
N
N
16.
Расчет термодинамических функцийE0 kT ln Z RT RT ln
Q
N
ln Z
ln Z
2 ln Q
H E0 U E0 PV kT 2
kT
V RT
RT
T
V
T
V
T
V
2
2
U
ln Z
ln Q
2 ln Z
2 ln Q
сv
2RT
2kT
kT
RT
2
2
T
T
T
T V
T V
V
V
V
2
2
H
ln Z
ln Q
2 ln Z
2 ln Q
ср
2 RT
R
2kT
kT
RT
2
2
T
T
T
T
T
p
p
p
p
p
17.
Энтропия НСl, S0298K,эксп. = 186,6 {Дж/моль/град}S
0
пост элек .
2 mkT
R ln
h3 N
3
2
V
5
R R ln z0 153,5
2
2
8
I kT
1
Sвр R ln
R 33,1
2
h
h i hkT 1
e
1
6
kT
6,7 10
Sкол R ln
R
h 1
h i
kT
kT
1 e
1 e
18.
Молекулярные параметры, нужные для расчета QМолекулярная масса, m – хим. анализ, масс-спектрометрия
Структура, момент инерции, I
– электронография, РСА
Квантовохимический
расчет!
- ИК- спектры,
КР - спектры
Частоты колебаний,
ν
Вырожденность основного электронного состояния, go
- расчет? УФ спектры
Энтальпия ∆H00
- калориметрия, закон Кирхгофа, расчет
19.
Учет изотопного распределения3
2
Qпост 2 mkT V
; Qвращ. расчет I !
3
N
Nh
Молекула Cl2
x(Сl235,35 ) 0,574, x(Сl235,37 ) 0,367, x(Сl237,37 ) 0,058
S (Cl2 ) x(Сl235,35 ) S Сl235,35 x(Сl235,37 ) S Сl235,37 x (Сl237,37 ) S Сl235,35
R x(Сl235,35 )ln x(Сl235,35 ) x(Сl235,37 )ln x(Сl235,37 ) x(Сl237,37 )ln x(Сl237,37 )
20.
Расчет константы равновесия21.
Расчет константы равновесияGT0 i i0 (прдукты) j 0j ( реагенты) RT ln K
i
i
QпостQврQколQэлQяд
Q
E0 RT ln RT ln
N
N
22.
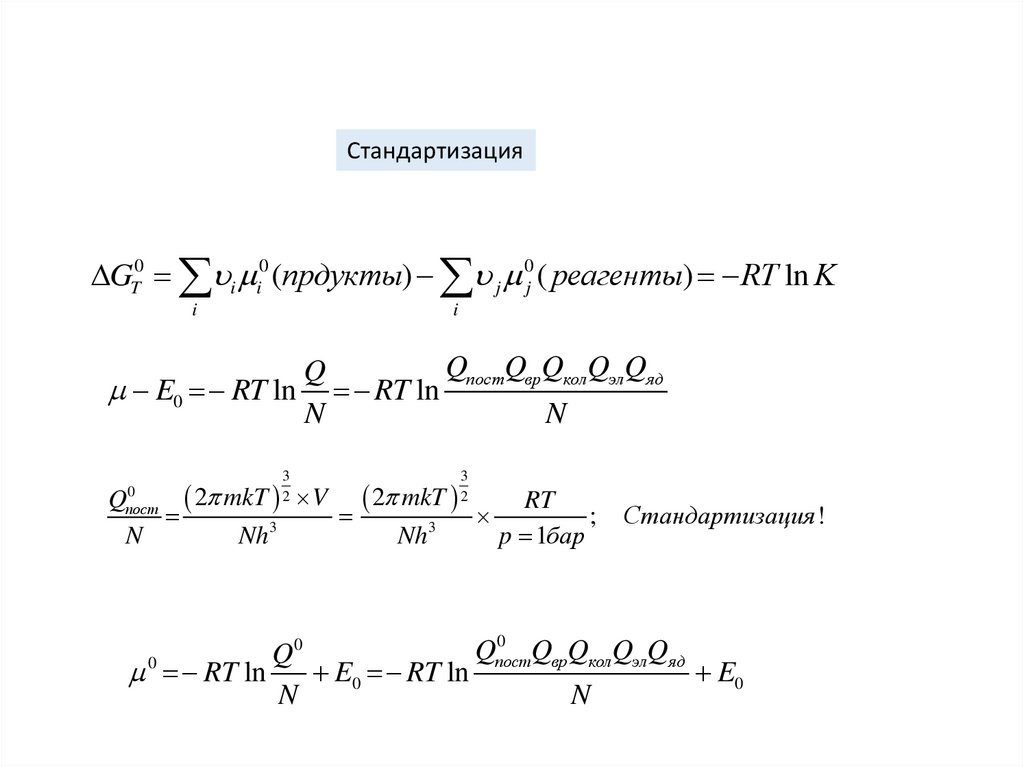
СтандартизацияGT0 i i0 (прдукты) j 0j ( реагенты) RT ln K
i
i
QпостQврQколQэлQяд
Q
E0 RT ln RT ln
N
N
3
2
3
2
2 mkT V 2 mkT
Q
RT
;
N
Nh3
Nh3
p 1бар
0
пост
Стандартизация !
0
0
Q
Q
постQвр QколQэлQяд
0
RT ln
E0 RT ln
E0
N
N
23.
2A B A2 BK e
GT0
RT
GT0 A02 B 2 A0 B0
0
0
Q
Q
постQвр QколQэлQяд
0
RT ln
E0 RT ln
E0
N
N
QA02 B ,пост
K
N
Q
N
0
A, пост
QA2 B ,врQA2 B ,колQA2 B ,эл g 0, A, яд g 0, B , яд
2
2
Q
QA,врQA,колQA,эл
N
0
B ,пост
e
QB ,врQB ,колQB ,эл g 0, A, яд g 0, B , яд
2
E0 H E0 ( A2 B) 2E0 ( A) E0 ( B)
0
0
E0
RT
24.
КH 2 (пара ),
H 2 (орто )
Q(чет) 1 5e
TK 0
6
вр
T
......
1140
p H 2 , пара g o , яд пара Qвр ( Н 2 , чет)
К
e RT
p H 2 , орто g o , яд орто Qвр ( Н 2 , нечет)
Q(нечет) 3e
H 00 орто пара 1,14кДж моль 1
2
вр
T
7e
12
вр
T
....
1
3
25.
Практические константы равновесия2 A B A2 B
K;
3
2
2 mkT
Q
RT
;
3
N
Nh
p 1бар
0
пост
Q p ,пост
K p K p 1бар ;
n
N
n
p 1бар
Kc K
;
RT
N
3
2
2 mkT RT
Q
p 1бар
N
Nh3
0
пост
0
Qс ,пост Qпост
p 1бар 2 mkT
N
N
RT
Nh3
Qc , A2 B ,пост
Kc
n 2
QA2 B ,врQA2 B ,колQA2 B ,эл
2
Qc , A,пост
Qc , B ,пост
QA,врQA,колQA,эл
QB ,врQB ,колQB ,эл
N
N
e
3
2
E0
RT
26.
Закон равнораспределения энергии постепеням свободы в идеальном газе
27.
СТЕПЕНИ СВОБОДЫ – это координаты молекулы в фазовом пространстве μ.КООРДИНАТЫ: поступательные px py pz qx qy qz и вращательные px py pz qx qy qz
У ИДЕАЛЬНОГО ГАЗА ЕСТЬ ТОЛЬКО КИНЕТИЧЕСКАЯ ЭНЕРГИЯ. ОНА ЗАВИСИТ ТОЛЬКО
от ИМПУЛЬСОВ.
В нашей задаче степени свободы – это поступательные px py pz и вращательные px py pz
СРЕДНЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА РАВНОМЕРНА РАСПРЕДЕЛЕНА МЕЖДУ
6-ю СТЕПЕНЯМИ СВОБОДЫ.
Колебательную и электронную энергию не рассматриваем (пока!)
28.
Расчет сумм по состоянию, Q.Qпост.
V
3 e
h
px2
2 mkT
dpx e
p 2y
2 mkT
dp y e
pz2
2 mkT
dp z
3
3
3
V
2 mkT аT 2 aT 2
h
1/3
Qвращ.
8
3 e
h
2
1
2
M x2
2 I x kT
dM x e
M y2
2 I y kT
2
8
I x kT
h
1
2
1
2
dM y e
M z2
2 I Z kT
dM z
2
8
I y kT
h
3
2
1
2
2
8
I Z kT
b1 b2 b3 T В T
h
3
2
1
2
29.
Расчет поступательной и вращательной теплоемкости2
2
U
ln Z
ln Q
2 ln Z
2 ln Q
сv
2RT
2kT
kT
RT
2
2
T
T
T
T
T
V
V
V
V
V
Qпост. aT
n /2
n
; ln Qпост. ln a ln T
2
n
Q вращ. ВT n/2 ; ln Qвращ ln В ln T
2
n
сV R ;
2
U E0
n число степеней свободы
n число степеней свободы
3
3
R поступательная;
R ( R ) вращательная
2
2
n
RT ;
2
3
3
RT поступательная;
RT ( R ) вращательная
2
2
30.
ЗАКОН РАВНОРАСПРЕДЕЛЕНИЯ это :1. Низкая характеристическая температура, близко лежащие
уровни энергии, возможность замены суммирования на
интегрирование
+
2. Конкретный вид интеграла:
Q
1/2
Ax
e
dx A
2
1/2
T
a
1
2
31.
ЗАКОН РАВНОРАСПРЕДЕЛЕНИЯ не РАСПРОСТРАНЯЕТСЯ наКОЛЕБАТЕЛЬНУЮ и ЭЛЕКТРОННУЮ ЭНЕРГИЮ
32.
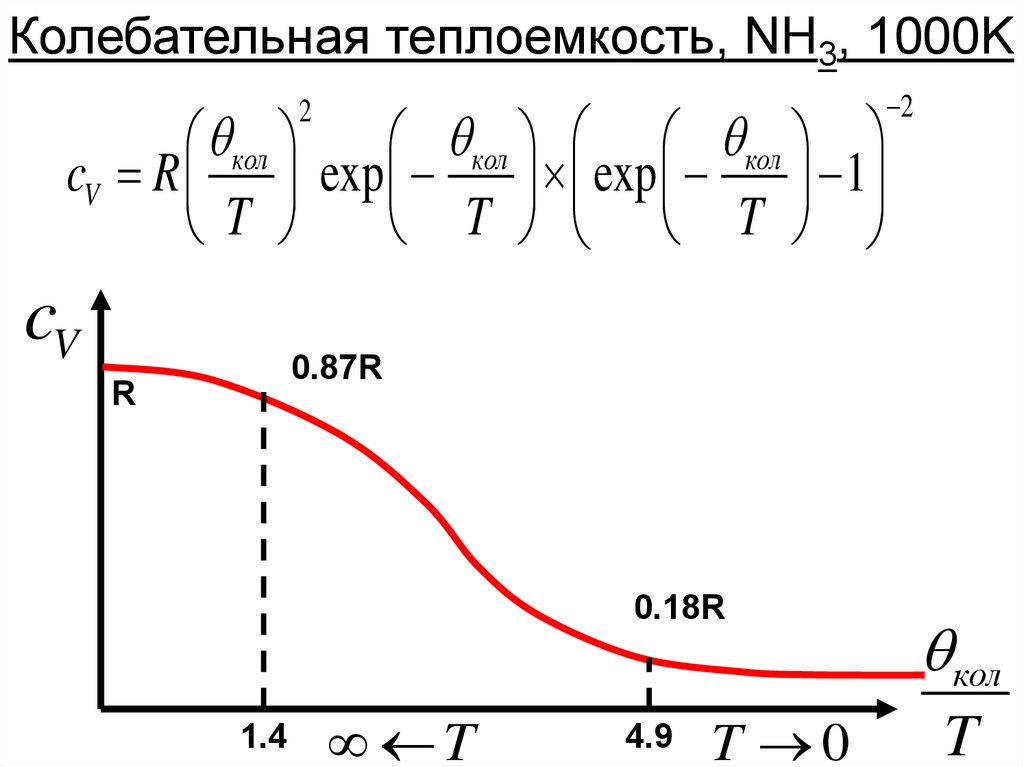
Колебательная теплоемкость, NH3, 1000Kкол
кол кол
cV R exp
exp
1
T
T T
2
cV
2
0.87R
R
0.18R
1.4
T
4.9
T 0
кол
T
33.
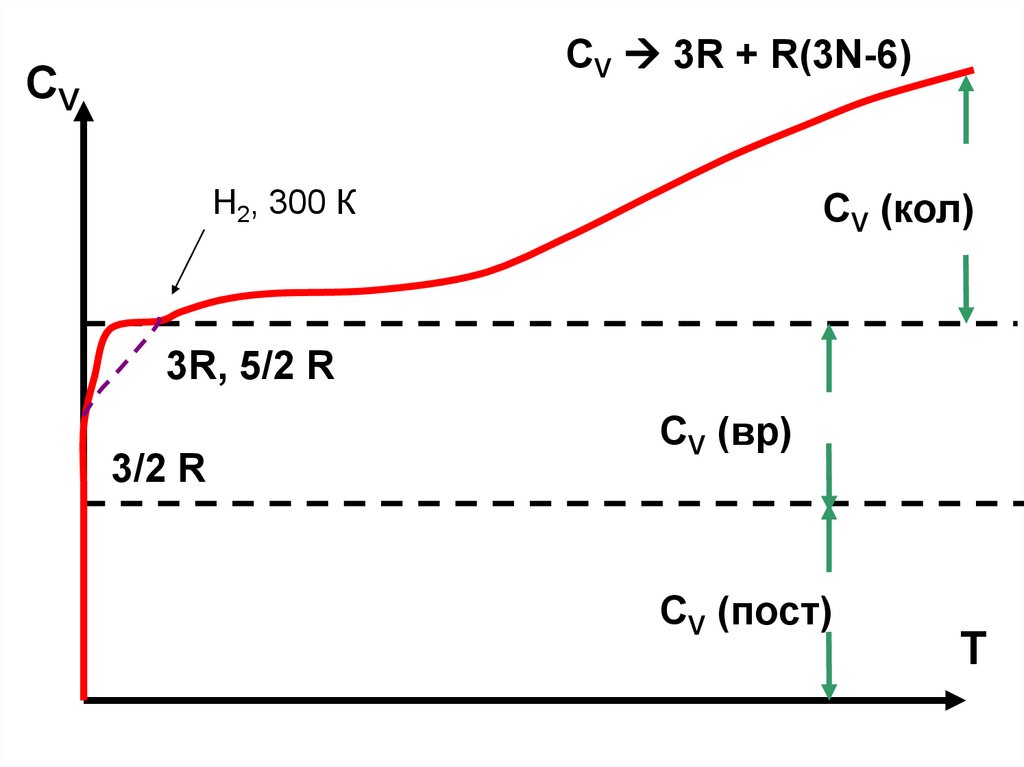
CV 3R + R(3N-6)СV
Н2, 300 К
CV (кол)
3R, 5/2 R
3/2 R
CV (вр)
CV (пост)
T
34.
РАСЧЕТ КОНФИГУРАЦИОННОГО ИНТЕГРАЛАдля
РЕАЛЬНОГО ГАЗА
35.
ЭНЕРГИЯ E и ИНТЕГРАЛ Z в ПРОСТРАНСТВЕ Ω :E E ( p1, x ; q1, x .. pi , y ; qi , y ... pN , z ; qN , z ...) Eкол Eвр Еэл E яд
E ( p1, x ; q1, x .. pi , y ; qi , y ... pN , z ; qN , z ...) E ( p1, x ;.. pi , y ... pN , z ) E (q1, x ..; qi , y ...qN , z ...)
Z Z p, q Z внут Z p Z q Z внут
Z e
E ( p1 x .. pNz )
kT
dp1x .. pNz e
E ( q1 x ..q Nz )
kT
dq1x ..qNz Z внут
36.
Конфигурационный интеграл :Z конф. e
E ( q1 x ..qNz )
kT
dq1x ..qNz
E ( p1, x ; q1, x .. pi , y ; qi , y ... pN , z ; qN , z ...) E ( p1, x ;.. pi , y ... pN , z ) E (q1, x ..; qi , y ...qN , z ...)
37.
Как мы будем учитывать зависимость энергии откоординат qi,j в фазовом пространстве?
E ( p1, x ; q1, x .. pi , y ; qi , y ... pN , z ; qN , z ...) E ( p1, x ;.. pi , y ... pN , z ) E (q1, x ..; qi , y ...qN , z ...)
Z конф. e
E ( q1 x ..qNz )
kT
dq1x ..qNz
E (q1x ..qNz ) U1,2 (q1x q1 y q1z ....q2 z ) U1,3 (q1x ..
38.
Как мы учитывали зависимость энергии откоординат qi,j в фазовом пространстве?
Qпост. e
( p ,q )
2 kTm
dpx dp y dpz dqx dq y dqz
h
Qпост. e
( p,q)
2 kTm
dpx dp y dpz dqx dq y dqz
h
V e
px2 p 2y pz2
2 kTm
3
3
e
px2 p 2y pz2
2 kTm
dpx dp y dpz dqx dq y dqz
h3
dqx dq y dqz e
px2 p 2y pz2
2 kTm
dpx dp y dpz
h3
VN
Qпост. qi , x ; qi , y , qi , z V ; Z пост. q1, x ; q1, y ,...qN , z ...
Z конф.
N!
dpx dp y dpz
h3
39.
Как мы будем учитывать зависимость энергии откоординат qi,j в фазовом пространстве?
Z конф. e
E ( q1 x ..qNz )
kT
dq1x ..qNz
E (q1x ..qNz ) U1,2 (q1x q1 y q1z ....q2 z ) U1,3 (q1x ..
Z конф. e
E ( q1 x ..q2 z )
kT
.... e
E ( q N 1 x ..q Nz )
kT
dq1x ..qNz
40.
1. Упрощаем интегралZ конф. e
E ( q1 x ..qNz )
kT
3N переменных
dq1x ..qNz
2. Вводим потенциал взаимодействия между
молекулами (атомы)
a
b
E (r ) 6 12
r
r
3. Считаем конфигурационный интеграл Zконф.
41.
Посчитаем давление:Для идеального газа:
Z конф. V
ln Z конф.
RT
F
ln V
kT
p RT
V
V T
V T
V
T
Для реального газа:
ln Z конф.
F
kT
p ?
V T
V
T
RT
a
2
V b V
42.
Упрощаем интеграл ….43.
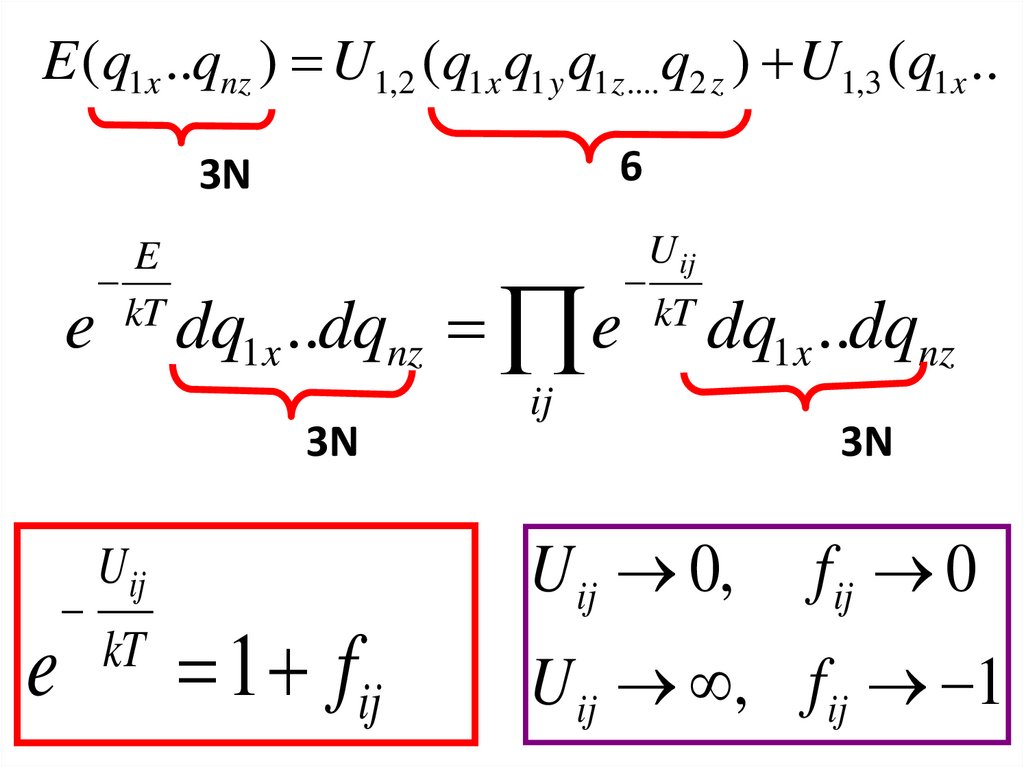
E (q1x ..qnz ) U1,2 (q1x q1 y q1z ....q2 z ) U1,3 (q1x ..6
3N
e
E
kT
dq1x ..dqnz e
3N
e
U ij
kT
1 fij
U ij
kT
dq1x ..dqnz
ij
U ij 0,
3N
fij 0
U ij , fij 1
44.
ee
E
kT
U ij
kT
1 fij
dq1x ..dqnz (1 f ij ) dq1x ..dqnz
ij
1 f ij f ij f kl ... dq1x dqNz
i
i
1 f ij dq1x dqNz ;
i
45.
1 fij fij f kl ... 1 f iji
i
i
3
1
U kl 0; fij 0, f ij f kl 0 (?)
46.
NN 2
1
f
dq
dq
V
V
f
dq
dq
ij
1
x
Nz
ij
ix
jz
q i
q i
3N
6
V V
N
N N 1
f ij dqix dq jz
2
q
6
N 2
V V
N
N 1
2
N
2
f dr
ij
x ,ij
r
drx ,ij dry ,ij drz ,ij r dr sin d d
2
dry ,ij drz ,ij
3
47.
V VN
N 1
2
N
2
4 f
2
ij
(r )r dr
r
2
2
N
N
N
N
N
V V
V 1
Zq
2V
2V
N2
N2
ln Z q N ln V ln 1
N ln V
2V
2V
Ln (1+x) ≈ х, x«1
48.
2N
ln Z q N ln V
;
2V
2
kTN
Fконф. E0 kT ln Z q kTN ln V
2V
49.
Вводим потенциал взаимодействиямежду молекулами (атомами) ….
50.
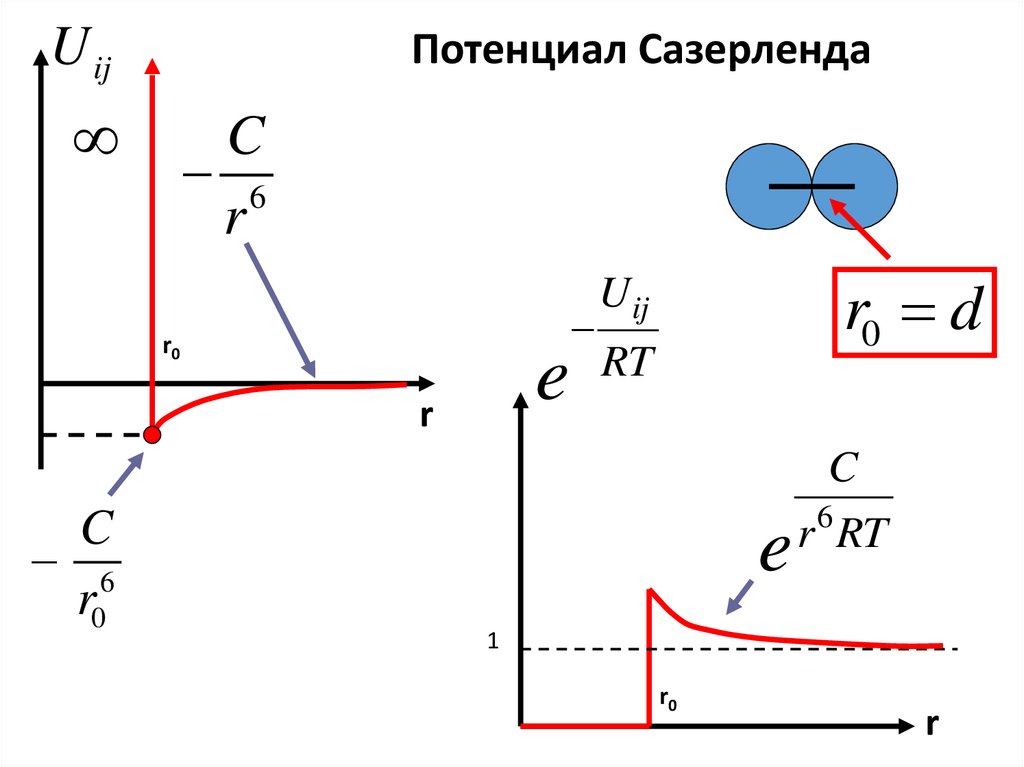
U ijПотенциал Сазерленда
C
6
r
r0
e
r
C
6
r0
r0 d
Uij
RT
e
C
6
r RT
1
r0
r



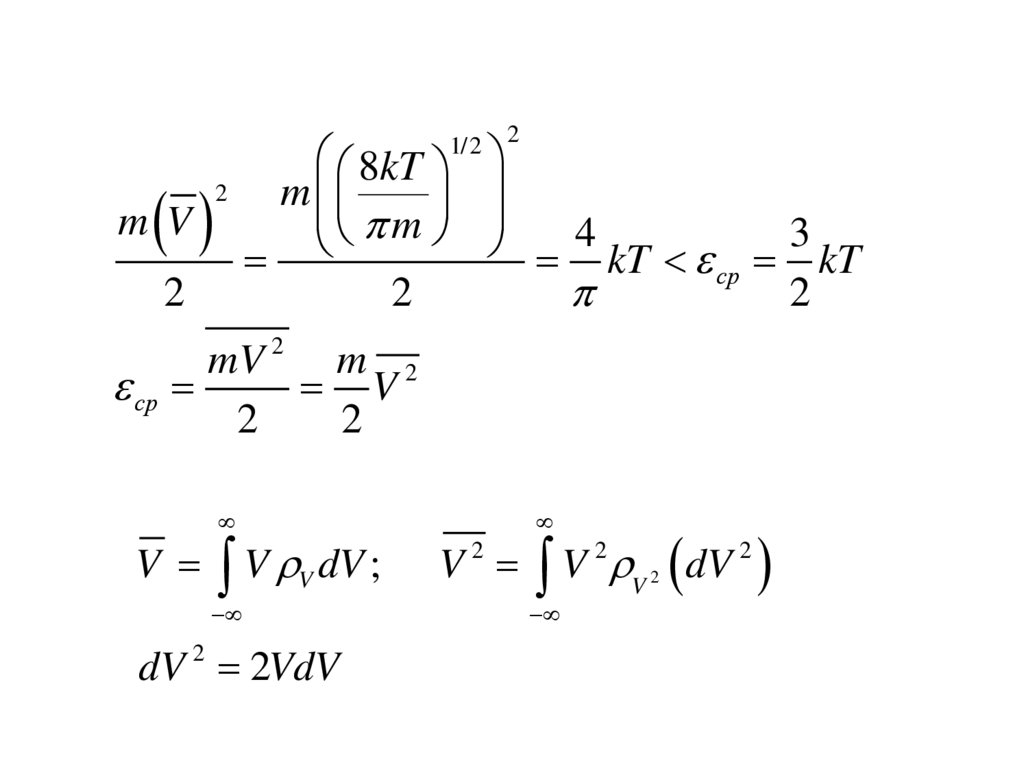
































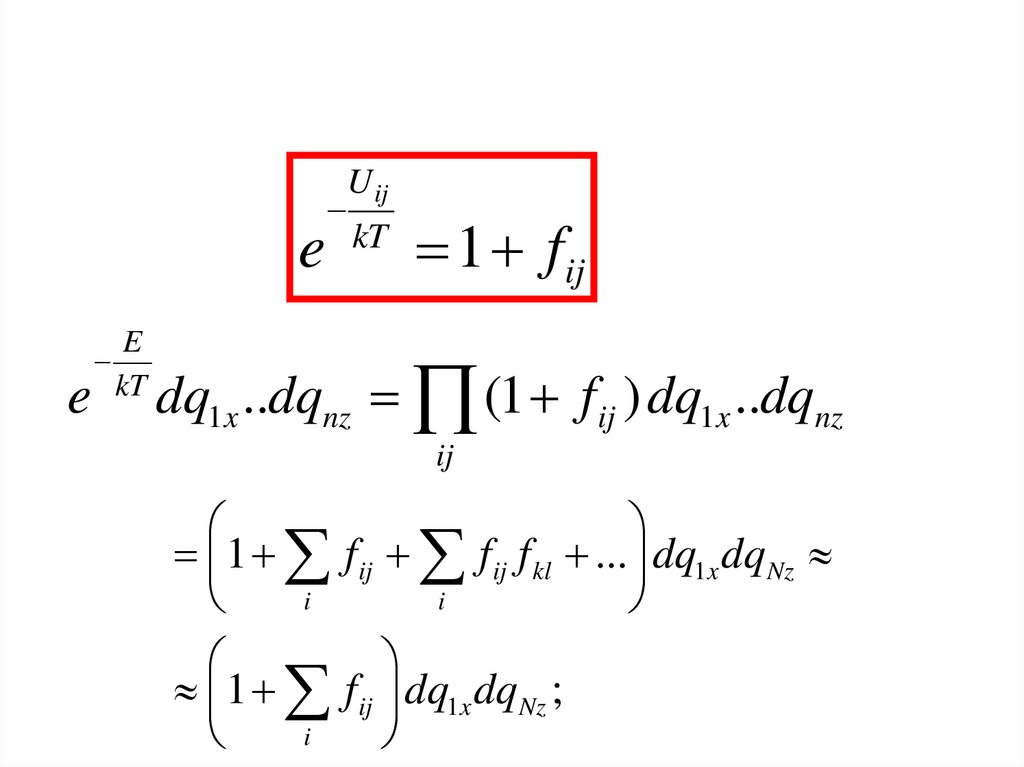

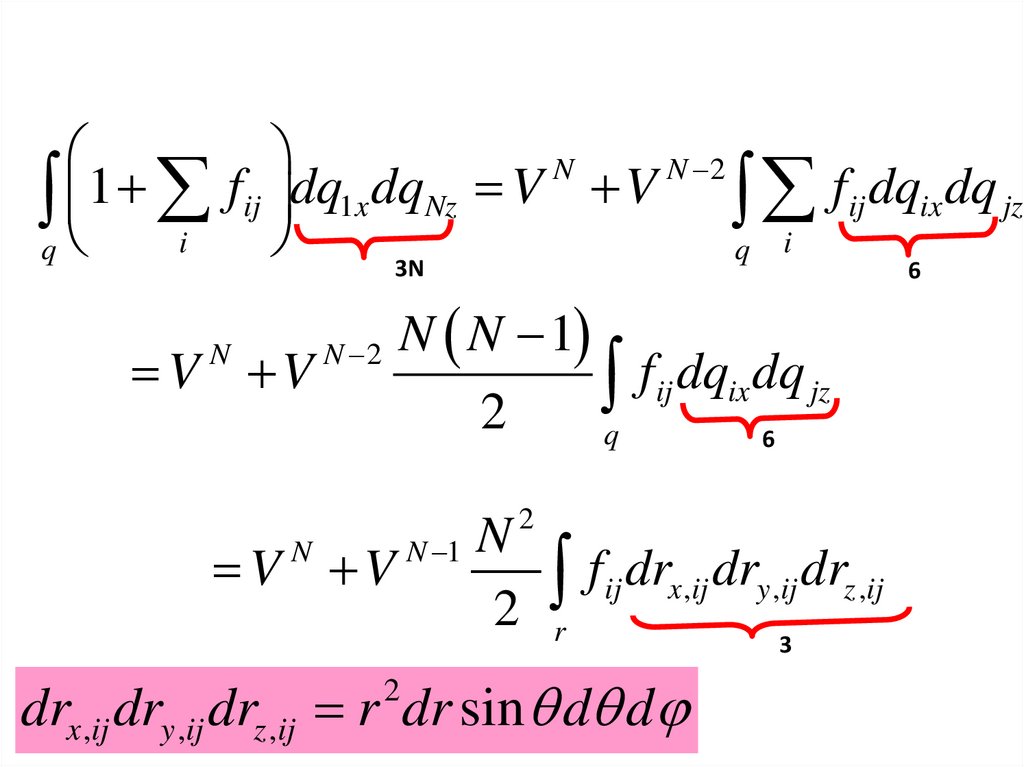
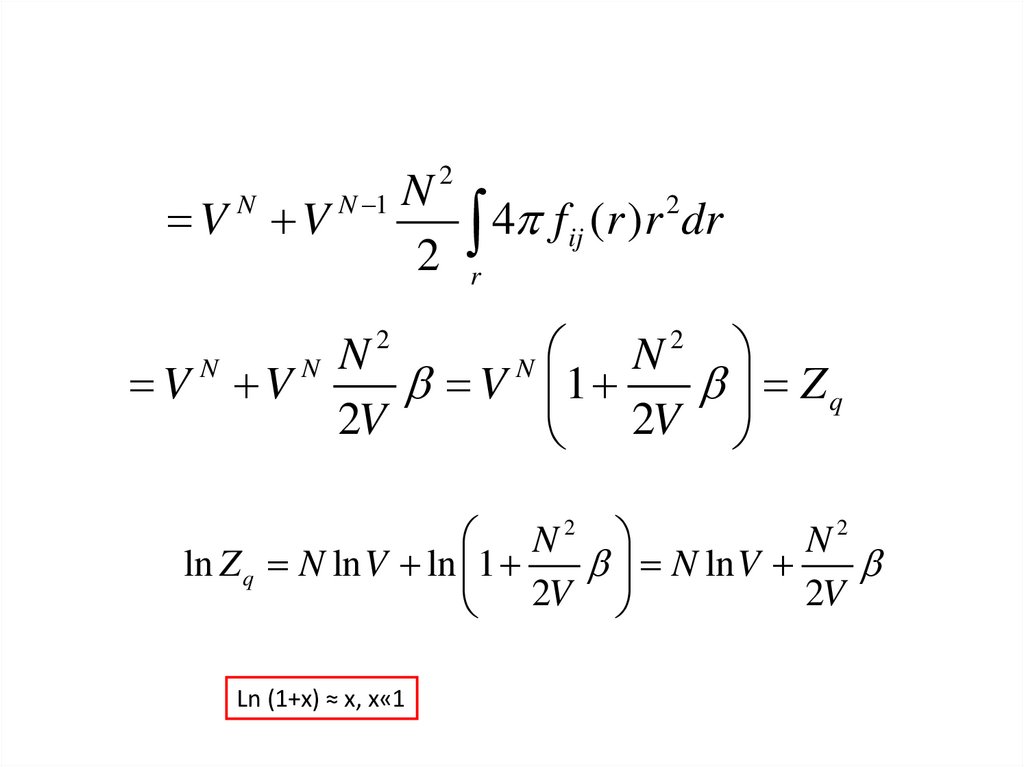
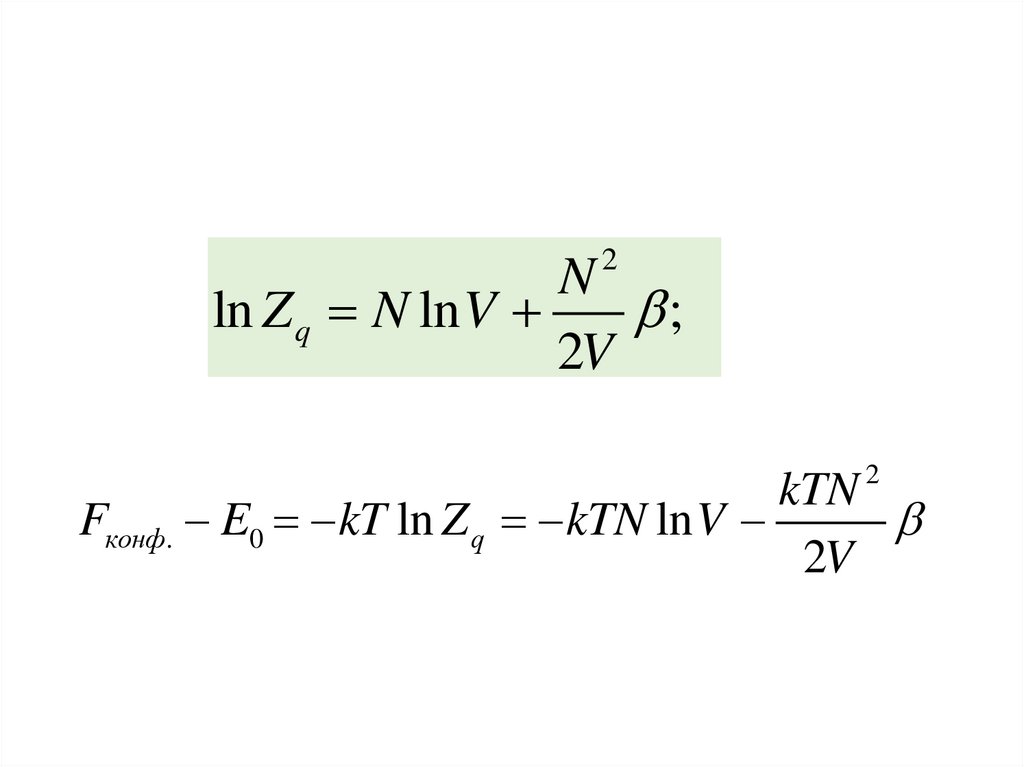

 Физика
Физика








