Похожие презентации:
Оптимальная оценка неэнергетического параметра сигнала. Тема 4: часть 2
1. Тема 4:
Часть 2:Оптимальная оценка неэнергетического параметра
сигнала.
Оптимальная оценка параметра сигнала с неизвестной
начальной фазой.
2.
Апостериорная плотность вероятностипараметра
wps ( ) c1 L( ) wpr ( ) c1c2 ec3 eq ( ) e
Ec ( )
G0
wpr ( ) Ceq ( ) e
Ec ( )
G0
wpr ( )
q ( ) EcG( )
Ec ( )
0
ln wps ( ) ln Ce e
wpr ( ) ln C q( )
ln wpr ( )
G0
T
2
q ( )
y (t ) s (t )dt корреляционный интеграл
G0 0
T
Eс ( ) s 2 (t )dt энергия сигнала
0
Оценка параметра по критерию максимума апостериорной вероятности:
ˆ argmax wps ( ) argmax ln wps ( )
3.
Оценка параметра полностью известногосигнала
(корреляционный приёмник)
y (t ) s (t ) n(t )
Коррелятор
1-й
канал
T
ln wps 1
0
s 1 t
ln wpr 1 Eс 1 G0
Опорный генератор
M-й
канал
T
ln wps M
ˆ
Оценка параметра:
ˆ , где
mˆ
mˆ argmax ln wps m
m 1, M
0
s M t
argmax
2 G0
Устройство
выбора
ln wpr M Eс M G0
4.
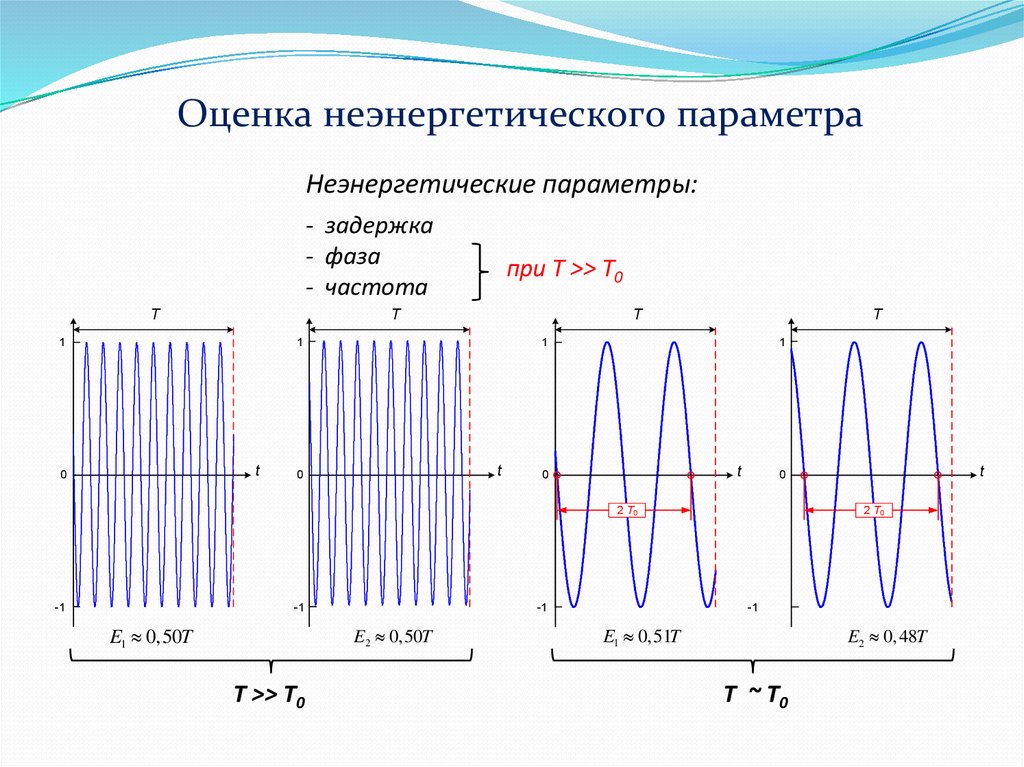
Оценка неэнергетического параметраНеэнергетические параметры:
- задержка
- фаза
- частота
T
при T >> T0
T
T
1
1
t
0
T
1
t
0
1
t
0
2 T0
-1
-1
E1 0,50T
-1
E2 0,50T
T >> T0
t
0
2 T0
-1
E1 0,51T
E2 0,48T
T ~ T0
5.
Оценка неэнергетического параметра сравномерным априорным распределением
ˆ arg max ps ( ) arg max ln ps ( )
2
ln wps ( ) ln c
G0
T
T
1
2
y
(
t
)
s
(
t
)
dt
s
(t ) dt ln w pr ( )
0
G0 0
При равномерном априорном распределении в интервале [λmin, λmax]
T
T
2
ˆ
arg max 2 y(t ) s (t )dt s (t )dt arg max 2R( ) Ec ( )
[ min , max ] 0
0
[ min , max ]
T
ˆ arg max R( ) arg max ( y(t ) s (t )dt )
[ min , max ]
[ min , max ] 0
Если Ес(λ)=const
6.
Корреляционный приёмникдля оценки задержки известного сигнала
Априорное распределение задержки
y (t )
равномерное на интервале min , max
T
1-й
канал
R 1
s t 1
1 min
T
M-й
канал
0
s t M
argmax
0
M max
R M
ˆ
7.
Эпюры напряжений в корреляционном приёмникепрямоугольного видеоимпульса
принятое колебание
y (t )
Эпюры напряжения в каналах
корреляционного приёмника
0
R( )
t
T
1-й канал
y (t ) s(t 1 )
t
T
1 0
y(t )s(t )dt
R( 1 )
y (t ) s(t m 1 )
T
1
t
(m-1)-й канал
m 1
t
y (t ) s (t
m 1
1 0
2
3
...
m 1
m m 1 ...
M
T
)dt
R( m 1 )
t
T
y (t ) s (t m )
m-й канал
m
t
T
y (t ) s (t
m
)dt
R( m )
t
T
y (t ) s(t m 1 )
(m+1)-й канал
m 1
mˆ argmax R ( m )
m 1, M
ˆ mˆ
t
T
y (t )s(t m 1 )dt
R( m 1 )
t
M-й канал
y (t ) s (t M )
M
T
t
y (t ) s (t
T
M
)dt
R( M )
t
T
14
8.
Корреляционный приёмникдля оценки неэнергетического параметра
y (t )
T
1-й
канал
R 1
s 1 (t )
1 min
T
M-й
канал
argmax
0
ˆ
R M
0
s M (t )
Априорное распределение параметра
равномерное на интервале min , max
M max
mˆ argmax R( m )
m 1, M
ˆ mˆ
9.
Оценка задержки радиосигнала с неизвестнойначальной фазой
Совместная оценка
задержки и фазы
Сигнал с неизвестной начальной фазой
s , (t ) U (t )cos 0 (t ) (t )
закон АМ
закон ФМ
ln wps ( , )
ˆ
max
ˆ , ˆ
ln wps max
min
2
0
ˆ
2
max
min
argmax ln wps ,
min , max
min , max
10.
Оценка задержки радиосигнала с неизвестнойначальной фазой
Усреднение по случайной начальной фазе
Апостериорная плотность вероятности задержки wps ( ) wps ( | )wpr ( ) d
0
Априорная плотность вероятность фазы wpr ( )
1
, 0,2
2
Условная апостериорная плотность вероятности:
wps ( | ) c e q ( , ) e
Eс ( , )
G0
wpr ( ) c e q ( , ) wpr ( )
const
wps ( ) c
2
1
q ( , )
e
d wpr ( )
2 0
11.
Оценка задержки радиосигнала с неизвестнойначальной фазой
Корреляционный интеграл
2
2
(t ) (t ) dt
q( , )
y
(
t
)
s
(
t
)
dt
y
(
t
)
U
(
t
)cos
,
0
G0 0
G0 0
0t (t ) 0
T
T
cos 0t (t ) 0 cos 0t (t ) ( 0 )
cos 0t (t ) cos 0 sin 0t (t ) sin 0
T
2
y (t )U (t )cos 0t (t ) dt cos 0
G0 0
Z c ( )
T
2
y (t )U (t )sin 0t (t ) dt sin 0
G0 0
Z s ( )
12.
Оценка задержки радиосигнала с неизвестнойначальной фазой
Корреляционный интеграл
q( , )
2
2
Z c ( )cos 0 Z s ( )sin 0
Z ( )cos ( ) 0
G0
G0
Z ( ) Z c ( ) 2 Z s ( ) 2 , Z c ( ) Z ( )cos ( ), Z s ( ) Z ( )sin ( )
Апостериорная плотность вероятности задержки
2
2
2
Z ( ) cos ( ) 0
1
1
G0
q ( , )
wps ( ) c
e
d wpr ( ) c
e
d wpr ( )
2 0
2 0
2
I0
G0
Z ( )
2
wps ( ) c I 0 Z ( ) wpr ( )
G0
13.
Оценка задержки радиосигнала с неизвестнойначальной фазой
Логарифм апостериорной плотности вероятности задержки
2
ln wps ( ) ln c ln I 0 Z ( ) ln wpr ( )
G0
При равномерном априорном
ln I 0 ( x)
ln I 0 x − монотонно
распределении задержки
2
ln wps ( ) const ln I 0 Z ( )
G0
Оценка задержки:
возрастающая
функция
x
0
ˆ argmax ln w ps ( ) argmax Z ( )
min , max
min , max
argmax Z ( ) 2 argmax Z c ( ) 2 Z s ( ) 2
min , max
min , max
14.
Оценка задержки радиосигнала с неизвестнойначальной фазой
Сигнал с задержкой 0 :
s 0 , (t ) U (t 0 ) cos 0 (t 0 ) (t 0 )
Алгоритм оценки задержки
T
Z c ( ) y (t )U (t )cos 0t (t ) dt
0
T
Z s ( ) y (t )U (t )sin 0t (t ) dt
0
Z ( ) Z c ( ) 2 Z s ( ) 2
ˆ argmax Z ( ) argmax Z c ( ) 2 Z s ( ) 2
min , max
min , max
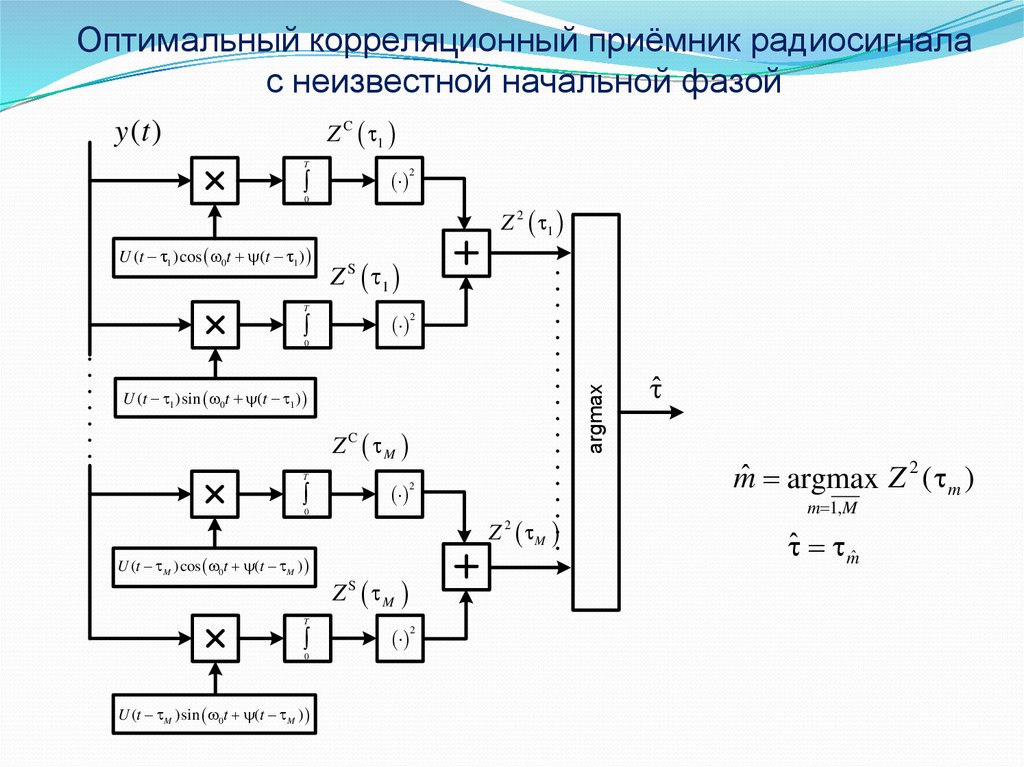
15.
Оптимальный корреляционный приёмник радиосигналас неизвестной начальной фазой
Z C 1
y (t )
T
2
0
U (t 1 )cos 0t (t 1 )
T
Z 2 1
Z S 1
2
0
argmax
U (t 1 )sin 0t (t 1 )
Z C M
T
mˆ argmax Z 2 ( m )
2
0
Z
U (t M )cos 0t (t M )
T
0
U (t M )sin 0t (t M )
Z S M
2
ˆ
2
M
m 1, M
ˆ mˆ













 Физика
Физика








