Знакочередующиеся и знакопеременные ряды

1.

Знакочередующиеся и
знакопеременные ряды.

2.

Знакочередующиеся ряды
Ряд называется знакочередующимся, если
любые два его соседних члена имеют разные
знаки, то есть
a1 a2 a3 a4 ... ( 1) n 1 an ... ( 1) n 1 an
n 1
или
a1 a2 a3 ... ( 1) an ... ( 1) an
n
n
n 1
an 0

3.

Признак Лейбница
Если члены знакочередующегося ряда убывают по
абсолютной величине a1 a2 ... an ... и
lim an 0, то ряд
n
( 1)
n 1
n 1
an сходится, а его сумма
не превосходит первого члена S a1

4.

1
n
3n 1
n 1
−
1
1
1
1
+
−
+
−⋯
22 52 82 112
1
1
1
1
>
>
>
>⋯
22 52 82 112
1.
2.
2
Все члены ряда убывают по абсолютной
величине
1
an
3n 1 2
1
1
lim an lim
0
2 lim
2
n
n
n
3n 1
9n 6n 1
По признаку Лейбница ряд сходится

5.

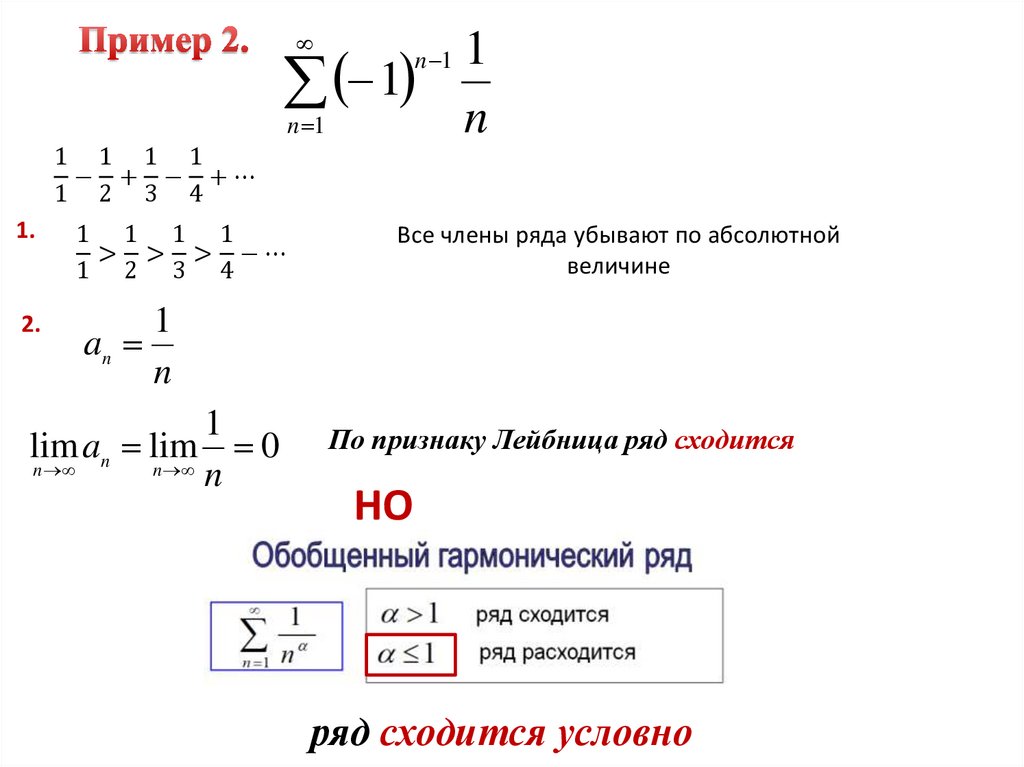
1
n 1
n 1
1
n
1 1 1 1
− + − +⋯
1 2 3 4
1.
1 1 1 1
> > > −⋯
1 2 3 4
2.
1
an
n
1
lim an lim 0
n
n
n
Все члены ряда убывают по абсолютной
величине
По признаку Лейбница ряд сходится
НО
ряд сходится условно

6.

1
k 5
k 1
k
k
1
1
1
1
− 1+
−
+
−⋯
5
2 ∙ 52 3 ∙ 53 4 ∙ 54
1.
1
1
1
1
>
>
>
>⋯
51 2 ∙ 52 3 ∙ 53 4 ∙ 54
2.
1
ak
k 5k
1
lim ak lim
0
k
k
k
k 5
3.
1
k
k 1 k 5
Все члены ряда убывают по абсолютной
величине
По признаку Лейбница ряд сходится
Рассмотрим ходимость положительного ряда,
используя признак Даламбера
ak 1
1
1
lim
:
k 1
k
k
k
ak
(k 1) 5
k 5
lim
k 5k
1
k
1
lim
lim
1
k
k
k
(k 1) 5 5 5
k 1 5
Положительный ряд сходится по признаку
Даламбера
1
k
k 5 ряд сходится абсолютно
k 1
k

7.

k
k
1
k 1
2k 1
2
3
2.
k
ak
2
k
1
lim q n 0, если q 1
n
4
1 2 3 4
...
3 5 7 9
2
3
4
1 2 3 4
...
3 5 7 9
1.
k
Все члены ряда убывают по абсолютной
величине
k
k
k
lim ak lim
0
k
k
2k 1
3. k
k 1 2 k 1
k
По признаку Лейбница ряд сходится
Рассмотрим ходимость положительного ряда,
используя радикальный признак Коши
сходимости
k
k
lim k ak lim k
Положительный ряд сходится по радикальному
k
k
2k 1
признаку Коши
k
1
lim
1
k
k
k
2k 1 2
k
1
k 1
2
k
1
ряд сходится абсолютно

8.

Знакопеременные ряды
Ряд
a
n 1
n
называется знакопеременным,
если любые его члены a n могут быть как
положительными так и отрицательными.

9.

Достаточный признак сходимости
Если ряд, составленный из абсолютных величин
членов данного ряда
сходится, то ряд
a
n 1
a
n 1
n
n
a1 a2 ... an ...
сходится.

10.

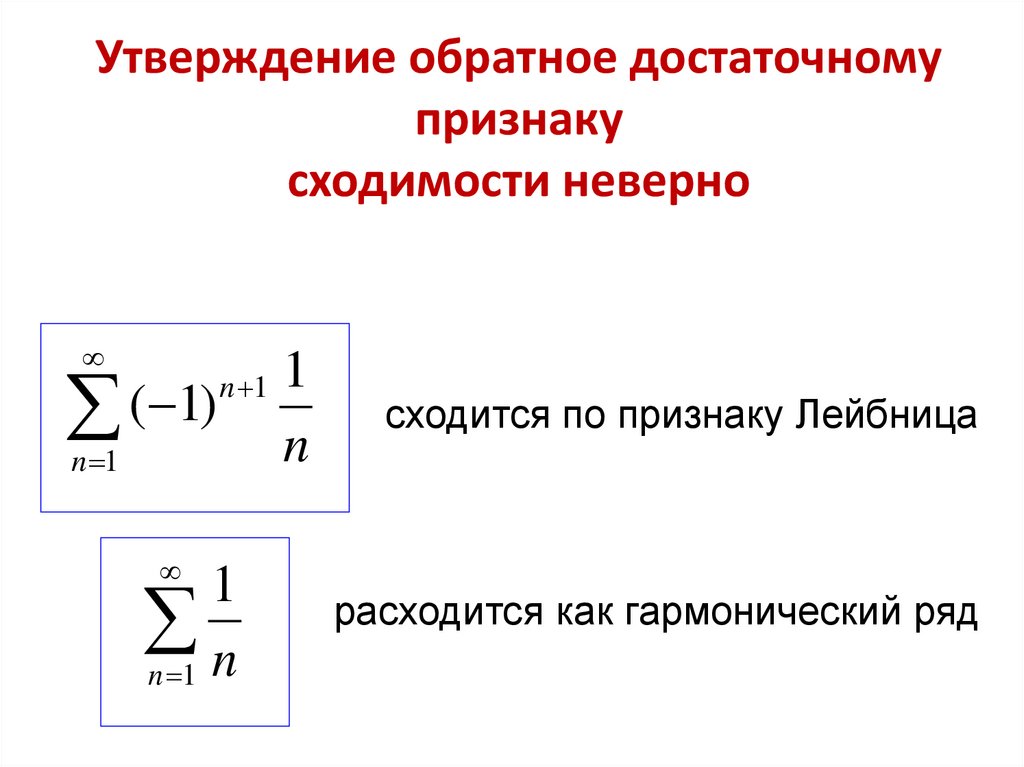
Утверждение обратное достаточному
признаку
сходимости неверно
( 1)
n 1
n 1
1
n
сходится по признаку Лейбница
1
n 1 n
расходится как гармонический ряд

11.

Ряд называется абсолютно сходящимся, если
сходятся ряды
a
n 1
n
и
a
n 1
n
Ряд называется условно сходящимся, если ряд
a
n 1
n
- сходится, а ряд
a
n 1
n
- расходится

12.

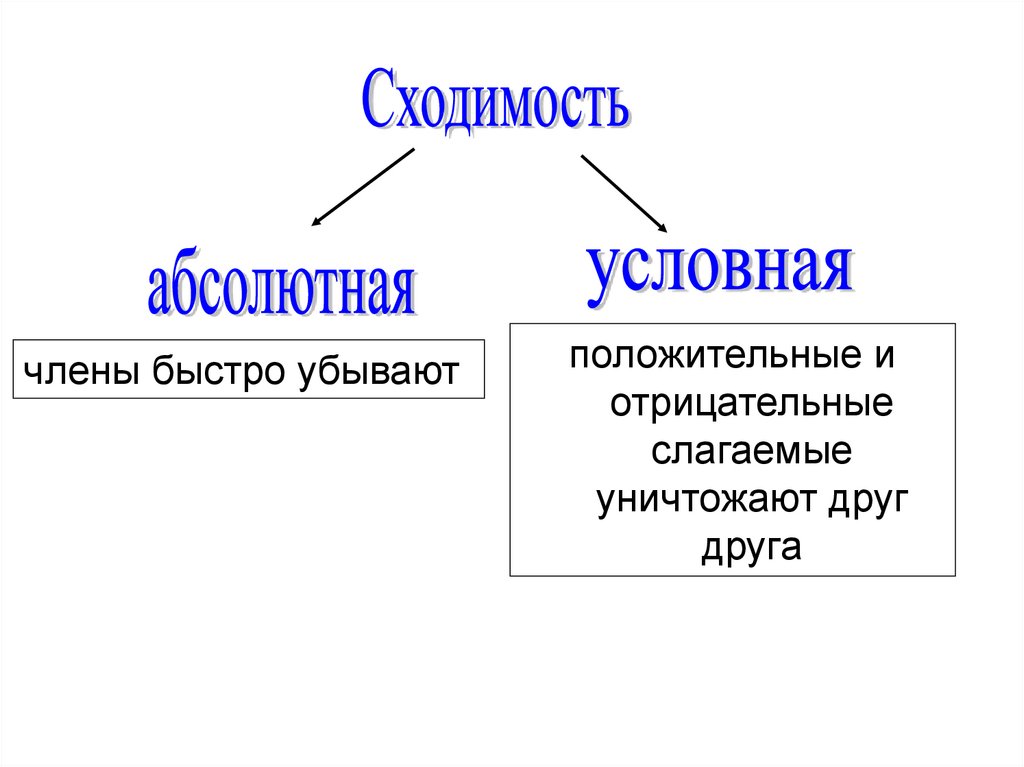
члены быстро убывают
положительные и
отрицательные
слагаемые
уничтожают друг
друга

13.

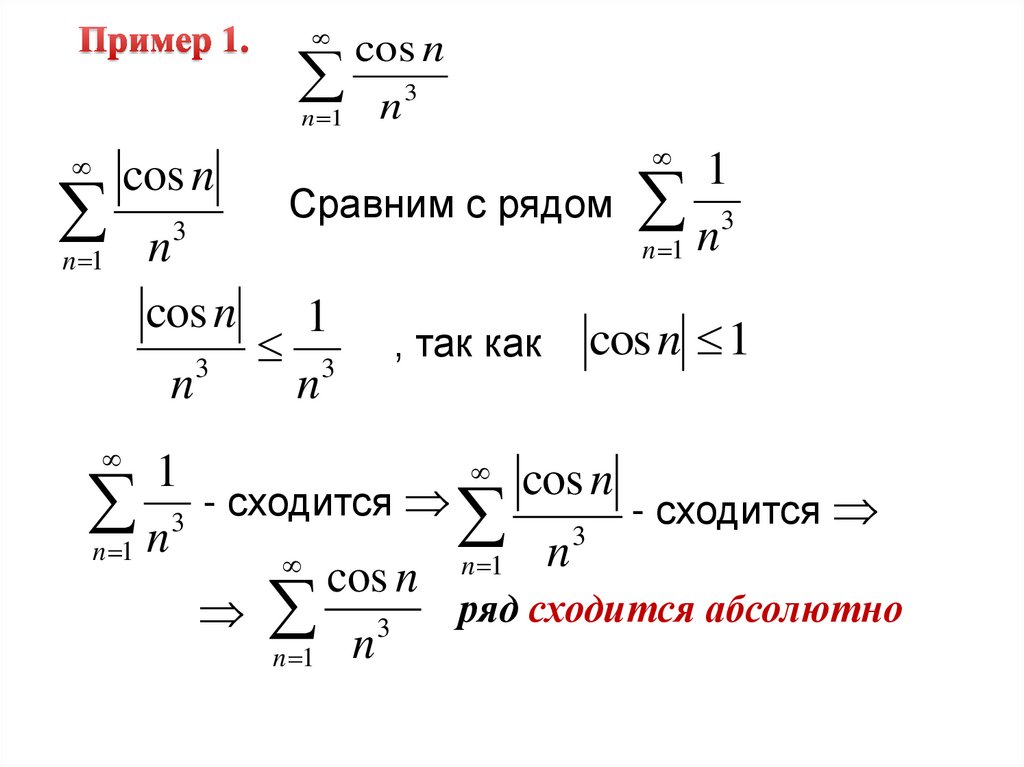
cos n
3
n
n 1
n 1
cos n
3
1
Сравним с рядом 3
n 1 n
n
cos n 1
3
3
n
n
, так как
cos n 1
cos n
1
- сходится
- сходится
3
3
n 1 n
n
n 1
cos n
3 ряд сходится абсолютно
n 1 n

14.

2k
1
3k 1
k 1
k
2 4 6 8
− + − +
−⋯
2 5 8 11
1. 2 4 6
8
> > >
>⋯
2 5 8 11
2.
2k
Все члены ряда убывают по абсолютной
величине
ak
3k 1
2k
2
lim ak lim
k
k
3k 1 3
По признаку Лейбница ряд расходится

15.

1
n 1
n2
2n
n 1
1 22 32 33
− + − −⋯
21 22 23 34
n2
n
n 1 2
Рассмотрим ходимость положительного ряда,
используя признак Даламбера
an 1
n 1 n 2
lim
lim n 1 : n
n
an k 2
2
2
n 1
lim
2n 1
n 2 2n 1 1
2 lim
1
n
2
n
2 2 n
2
n
2
2
n
Положительный ряд сходится по признаку
Даламбера
n 1
1
n 1
2n
n2
ряд сходится абсолютно

16.

1
2
3n 5
2n
1
n
n 1
1
2
2
n
3
3 9 19
8 17 32
2n 2 1
2
n 1 3n 5
n
Рассмотрим ходимость положительного ряда,
используя радикальный признак Коши
n
2
2
n
1
2
n
1 2
n
n
lim an lim 2
1
lim
2
n
n
n
3n 5 3
3n 5
2
Положительный ряд сходится по признаку Коши
1
2
3n 5
2n
1
n 1
n
2
n
ряд сходится абсолютно

17.

Домашнее задание
1. Запишите общую формулу ряда. Используя признак Лейбница, исследуйте на
сходимость ряд:
1 1
1
1 1 1
b
)
1
.....
a)1
.....
5
25
125
3 9 27
2. Напишите ряд в развёрнутом виде. Исследуйте на абсолютную и условную
сходимость ряд:
1
n 1
n 1
1
n 1
3n
4
n
1
n 1
1
2n 1
1
2n 1 3
n 1
n
n
n
1
n
2n 1
n 1
n
n
1
n 1
2n 1
n