Похожие презентации:
Электродинамика. Электрическое поле. Магнитное поле
1.
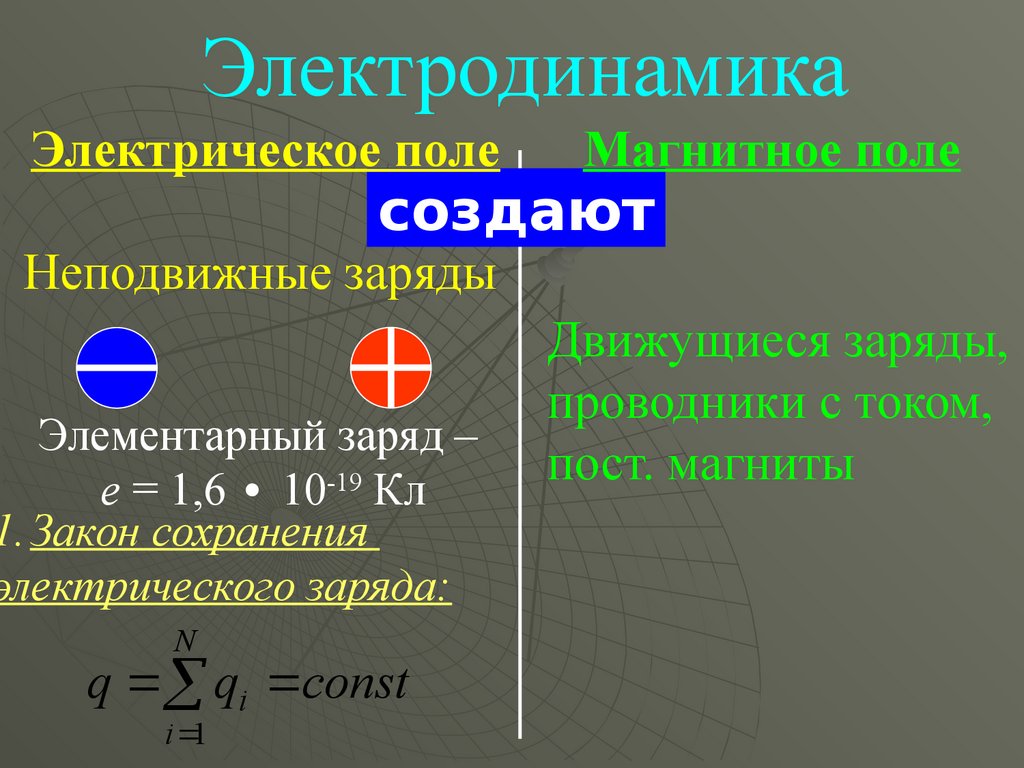
ЭлектродинамикаЭлектрическое поле
Магнитное поле
создают
Неподвижные заряды
Элементарный заряд –
е = 1,6 ∙ 10-19 Кл
1.Закон сохранения
электрического заряда:
N
q qi const
i 1
Движущиеся заряды,
проводники с током,
пост. магниты
2.
Равномерно распределенный заряда) линейное распределение
dq
d
q d
б) распределение по поверхности
dq
dS
q dS
S
в) распределение по объему
dq
dV
q dV
V
3.
обнаруживают по действию назаряженные тела
Закон Кулона:
В векторной форме :
q1 q2
F k
r
3
r
В скалярной форме :
q1 q2
F k
r2
2
1
Н
м
k
9 109
4 0
Кл 2
0 8,85 10
12
Ф
м
проводники с током,
рамки с током или
магнитные стрелки
0 I1I 2
F
2 r
сила, действующая на
единицу длины двух
взаимодействующих
параллельных проводнико в
с током
μ0 = 4π•10 -7Гн/м
4.
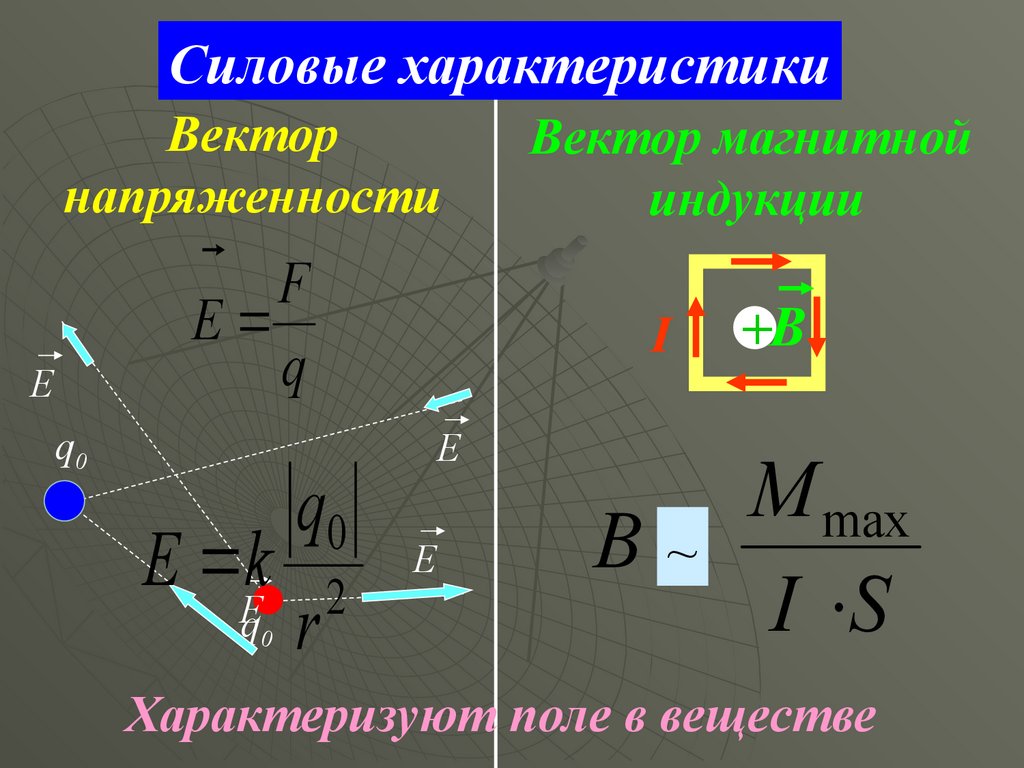
Силовые характеристикиВектор
напряженности
F
E
q
E
q0
q0
E Ek 2
q r
0
Вектор магнитной
индукции
I
E
E
B
~
+B
M max
I S
Характеризуют поле в веществе
5.
Векторэлектрической индукции
Вектор напряженности
Н
D
Характеризуют поле в вакууме
D 0 E
B 0 H
6.
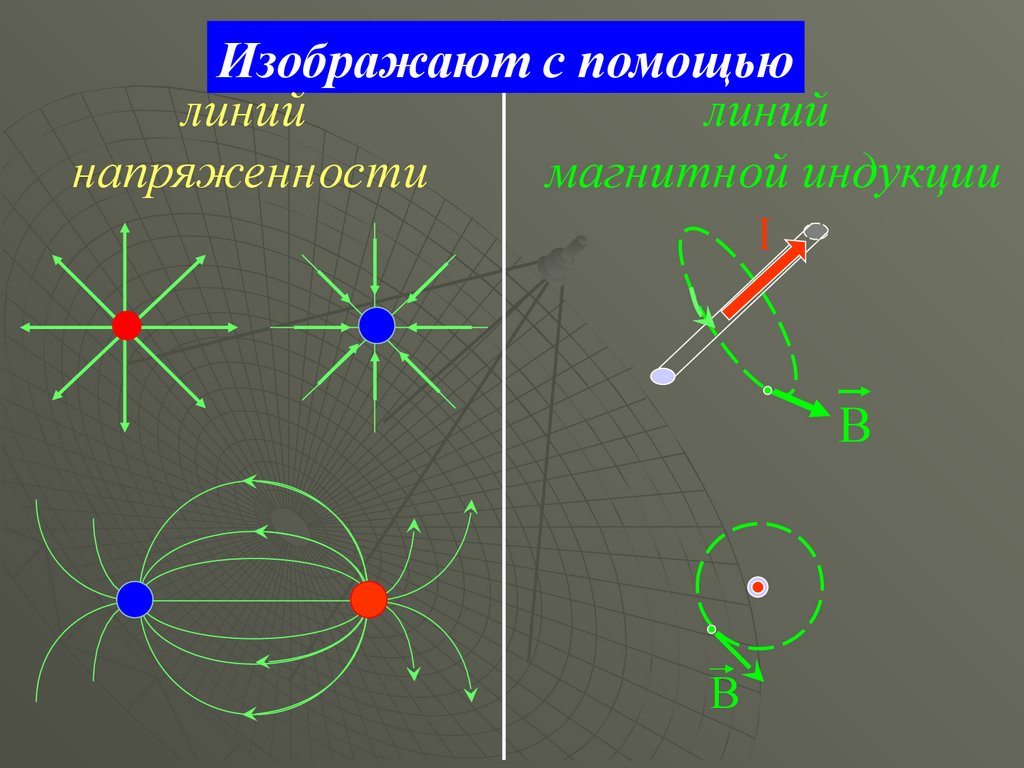
Изображают с помощьюлиний
линий
напряженности
магнитной индукции
I
В
В
7.
Принцип суперпозицииi n
n
E E1 E2 Ei En Ei B B1 B2 ... Bi ... Bn Bi
i 1
i 1
E2
E
φ
r1
B2
А
E1
q1
B1
r2
q2
E E1 E2 ;
А
I2
I1
B B1 B2
8.
nЕi 0
Е lim Еi
n
Еi 0
Е dE
n
B lim
Bi 0
Bi
n
Bi 0
B dB
9.
Закон Био-Савара-Лапласа (БСЛ)Y
dℓ I
I
Rdl
r
r
dBdBdB
β A
0 I dl r
x
dB
3
4
r
0 I dl
dB
2 sin
4 r
B dB
sin 1
0 I d
sin ;
2
4 0
r
0 I d
0 I sin 2
B
sin
d
X 4 r 2
2
4 r
2 R
0 2 R I sin 0 I
R
B i dB
sin
2 x j dB y2 k2 dBz
4
2 R x
r
I d
dB
4 r
x dB sin
2
IR
0 0;
dB y
dB
3 z
2
2
2 R x 2
0
10.
Задания2.1.Определите
индукции
магнитного
Определитенаправление
знак заряда,вектора
электрическое
поле
которого
поля,
созданного
током, влиний
указанных
на рисунке точках
изображено
с помощью
напряженности
А
I
С
В
11.
Методы расчетаТеорема Гаусса
1
E d S qi внутр.
0
S
E dS
S
n
Е
α
Е
d E dS E dS cos
B dS 0
s
Ф B dS B dS cos
S
s
n α
B
12.
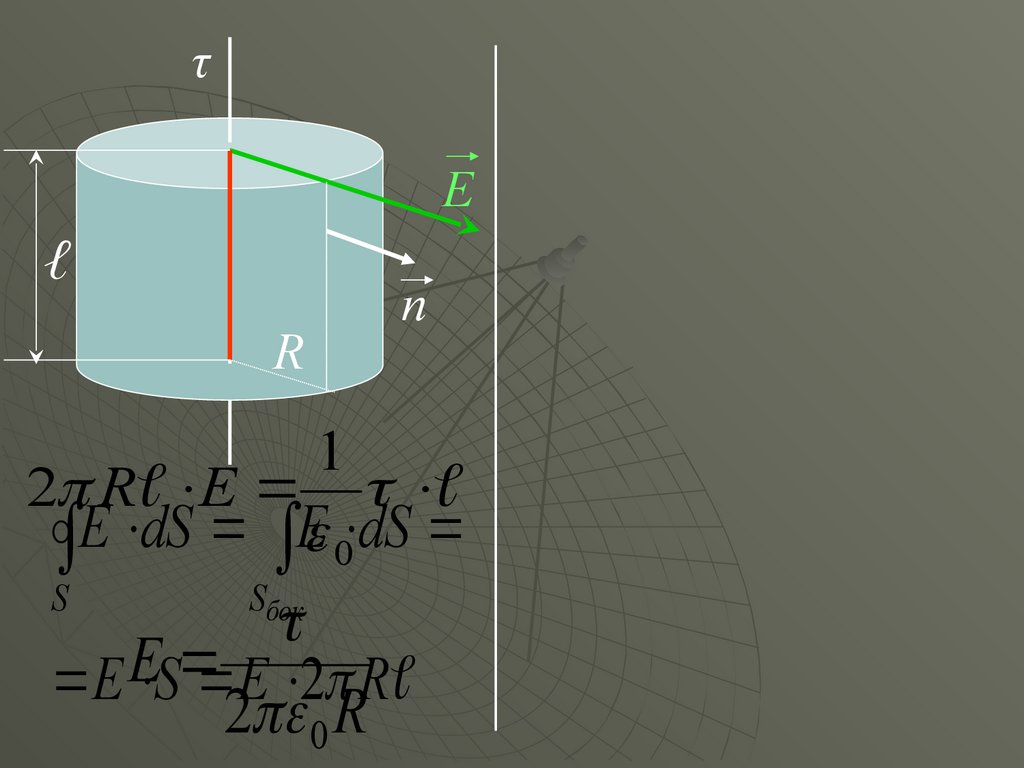
τЕ
ℓ
R
n
1
E
2 R
E dS E 0 dS
S
Sбок
E E S E 2 R
2 0 R
13.
1. Определите поток вектора напряженности череззамкнутую поверхность для случая, изображенного на
2. Стержень длиной ℓ равномерно заряжен с линейной
рисунке.
3. В центре куба находится электрический диполь.
плотностью заряда τ. Определите заряд стержня.
Определите поток вектора напряженности через
поверхность куба.
Е
14.
Теорема о циркуляцииE dr 0
B d 0 I внутр
Поле потенциально
Поле непотенциально
A W
W
Дж
q q0
В
W k
q
Кл
r
A q 2 1
q
q
k q0 U
E drr
B
d
B
d
cos
0
2 rB
I
r
B
2 r B 0 I
0 I
B
2 r
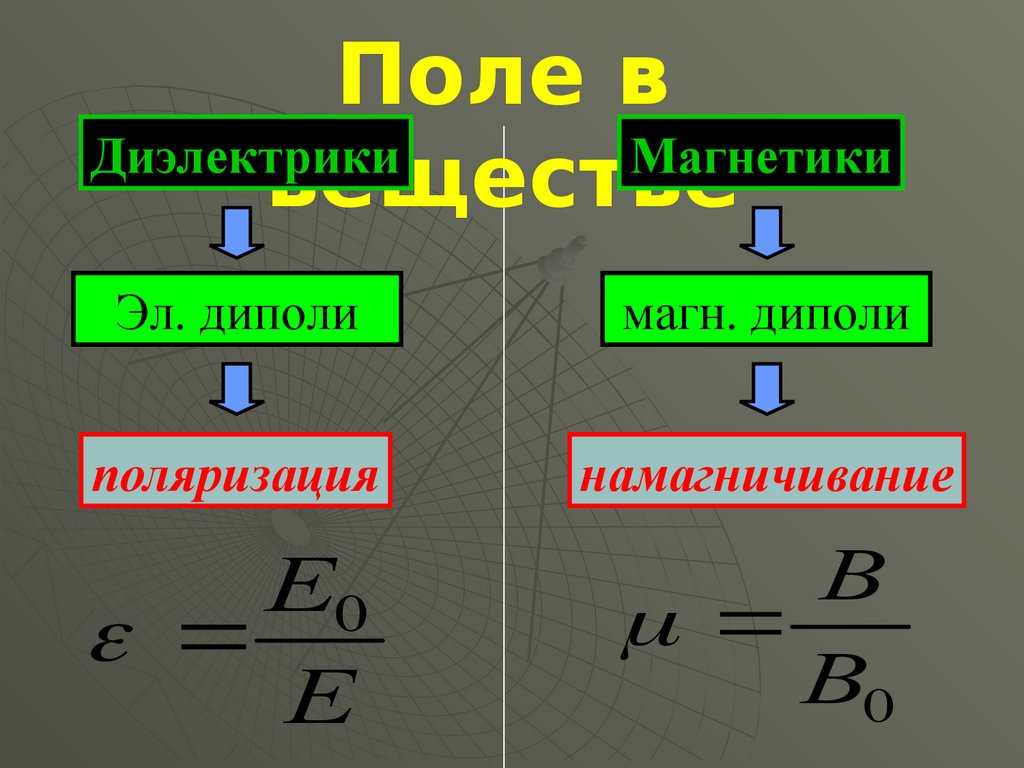
15.
Поле вДиэлектрики
Магнетики
веществе
Эл. диполи
магн. диполи
поляризация
намагничивание
Е0
Е
В
В0
16.
Энергия поля2
2
q C
q
W
2
2
2
2
qU q
CU
W
2
2C
2
0 E
w
2
2
2
0 E
W
dV
2
2
LI
W
2
2
2
B
w
2 0
B2
W
dV
2 0
17.
1. Какая из формул позволяет определить циркуляциюВектора
индукции
магнитного
по контуру?
2. Соленоид
длиной
ℓ имеет nполя
витков
на единице
длины.
I. Определите
соленоиду
По
течет ток
циркуляцию
индукции
по
замкнутому
B
d
;
1.
E
d
B
d
S
;
2.вектора
3.
4. E dS ;
контуру, изображенному на рисунке.
S
S
ℓ
I
18.
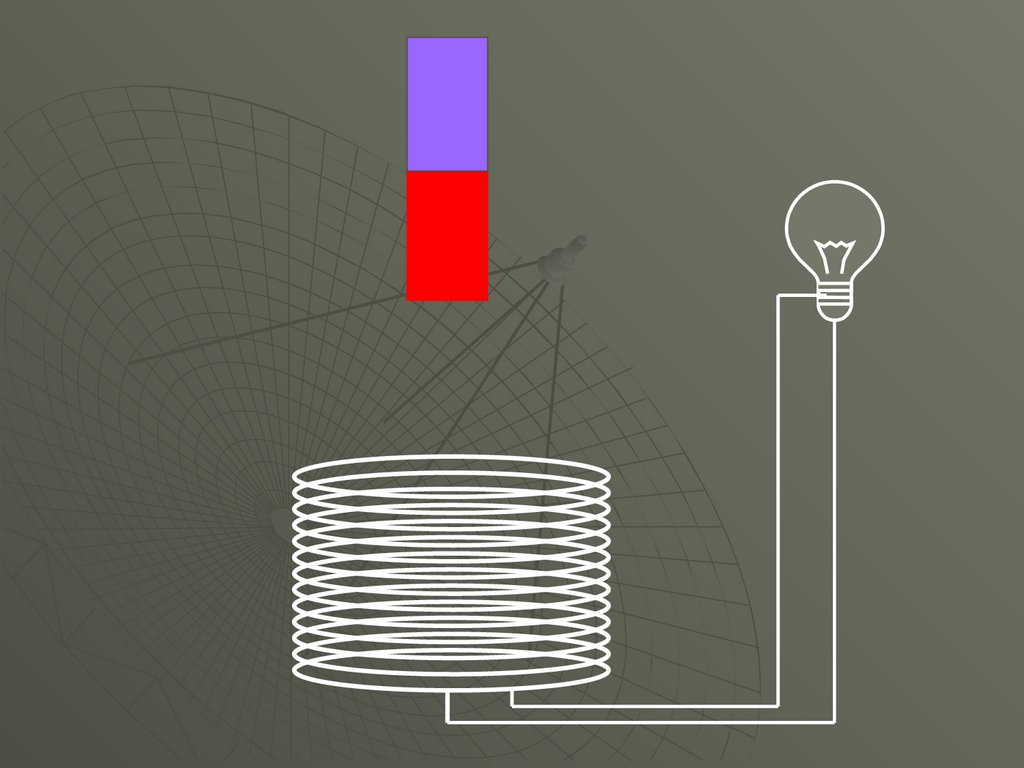
Явлениеэлектромагнитной
индукции
19.
20.
t t 2 t1Среднее
значение
э.д.с. в интервале времени
Закон
электромагнитной
индукции
Фарадея.
Для простого контура:
i
2 1
t 2 t1
t
B2 S 2 cos 2 B1 S1 cos 1
t 2 t1
Для сложного контура:
i
2 1
t 2 t1
t
21.
Мгновенное значение э.д.с. индукции в момент времени t:Для простого контура:
d
i lim
t
dt
t 0
Для сложного контура:
d
i
dt
N
22.
Φ1 ~ N 1Φ2 ~ N2
N 2 > N1
B
Bi
23.
1.B S
x
S x
d d B x
dx
i
B B
dt
dt
dt
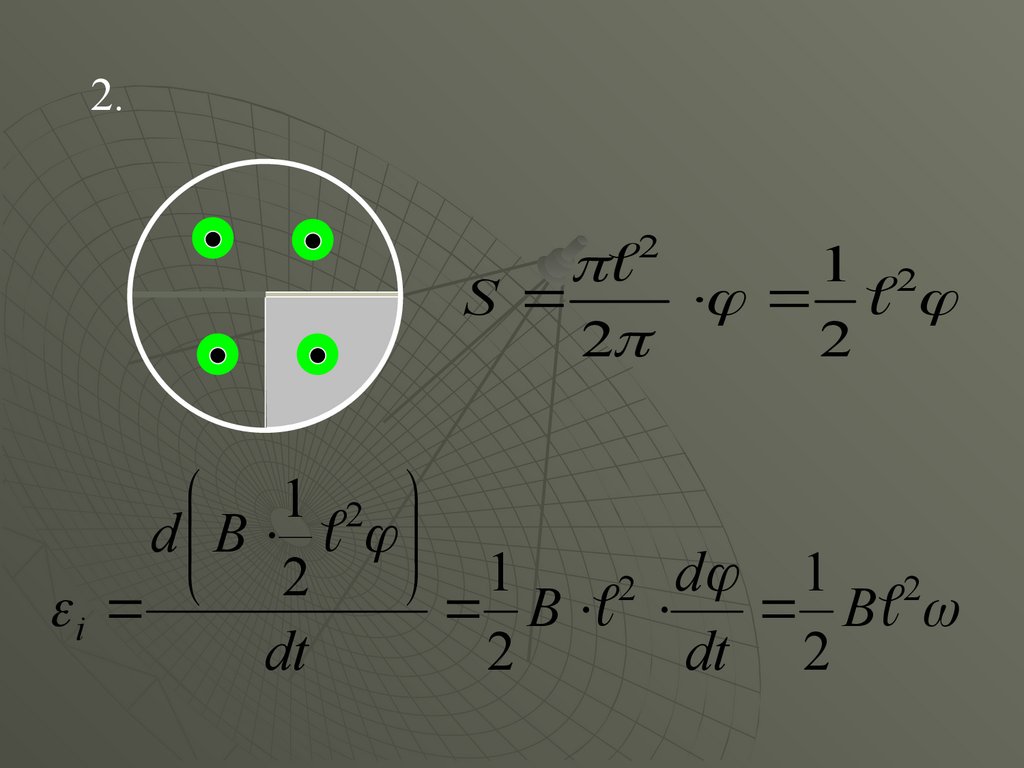
24.
2.2
1 2
S
2
2
1 2
d B
1
1 2
2
2 d
i
B B
dt
2
dt 2
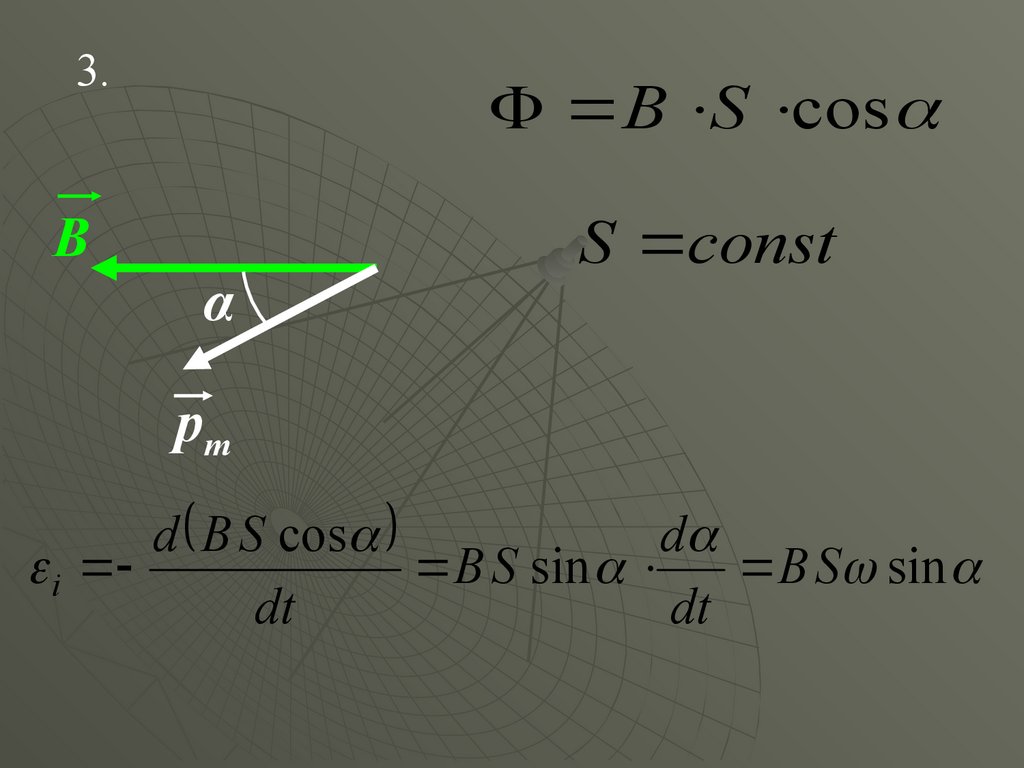
25.
3.B S cos
B
α
S const
pm
d B S cos
d
i
B S sin B S sin
dt
dt
26.
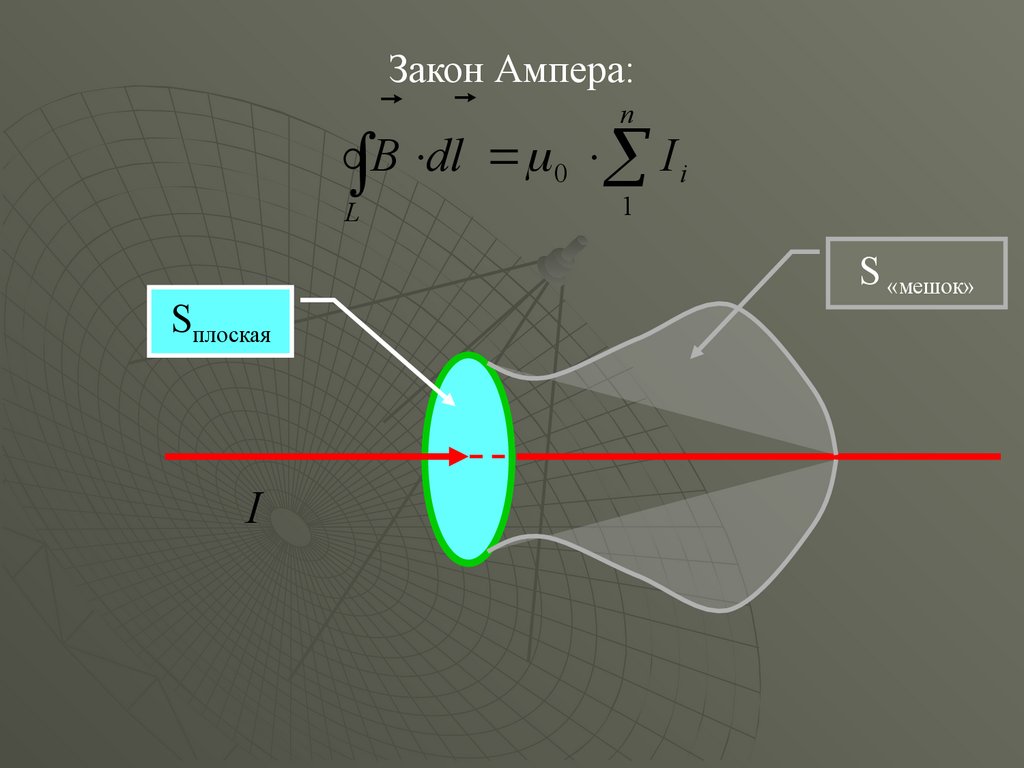
Закон Ампера:n
B dl 0 I i
L
Sплоская
I
1
S «мешок»
27.
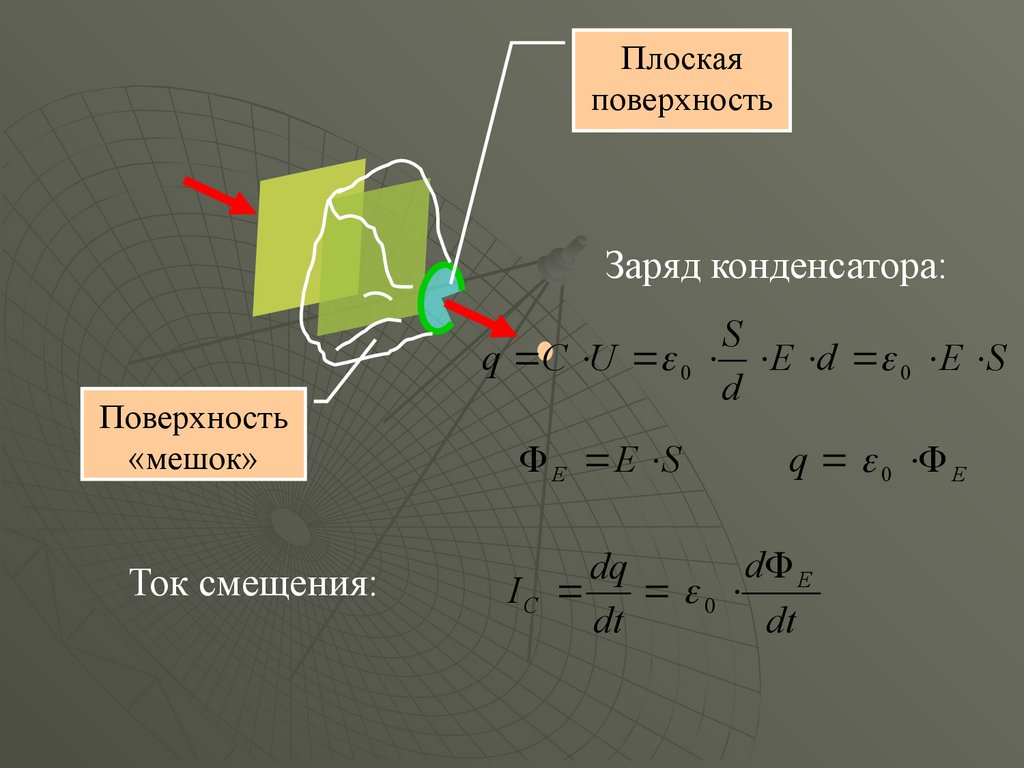
Плоскаяповерхность
Заряд конденсатора:
Поверхность
«мешок»
Ток смещения:
S
q C U 0 E d 0 E S
d
E E S
q 0 E
d E
dq
IC 0
dt
dt
28.
Поле неоднородное:E E dS
S
d E
dq
d
IC 0
0 E dS
dt
dt
dt S
29.
Закон Ампера с учётом тока смещения:n
B dl 0 I i 0 I I C
L
1
d E
B dl 0 I 0 0
dt
L
d
B
d
l
I
E
d
S
0
0
0
L
dt S
30.
Обобщенный закон Фарадея:d
d
Ei dl
B dS
dt
dt S
L
Переменное
Магнитное
магнитное
поле поле
Переменное
Электрическое
электрическое
поле поле
31.
Система уравнений Максвелла:i n
q
i 1
E dS
0
S
B dS 0
i
(1)
(2)
S
d
Ei dl
B dS
dt S
L
d
B dl 0 I 0 0 E dS
dt S
L
(3)
(4)
32.
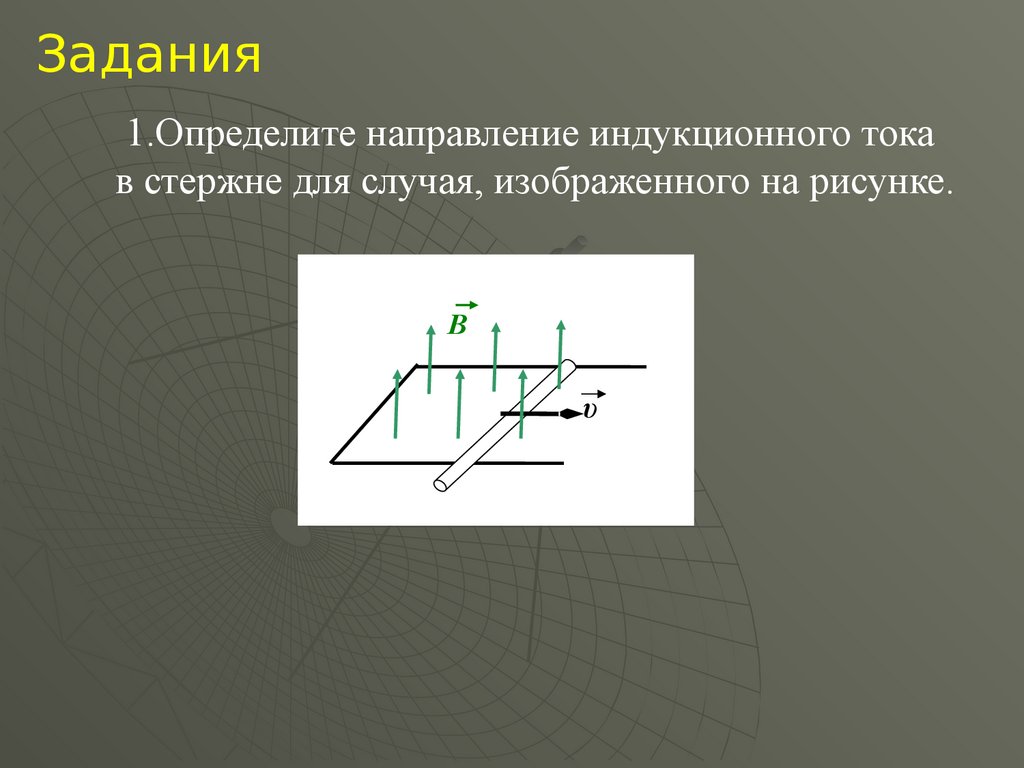
Задания1.Определите направление индукционного тока
в стержне для случая, изображенного на рисунке.
B
υ
33.
2. Какое из уравнений Максвелла, записанных ниже,является законом электромагнитной индукции
1 N
а)
б)
d
E dS qi
E d
B dS
S
в)
0 i 1
B dS 0
S
dt
S
d
г) B d 0 I 0 0
E dS
dt S




















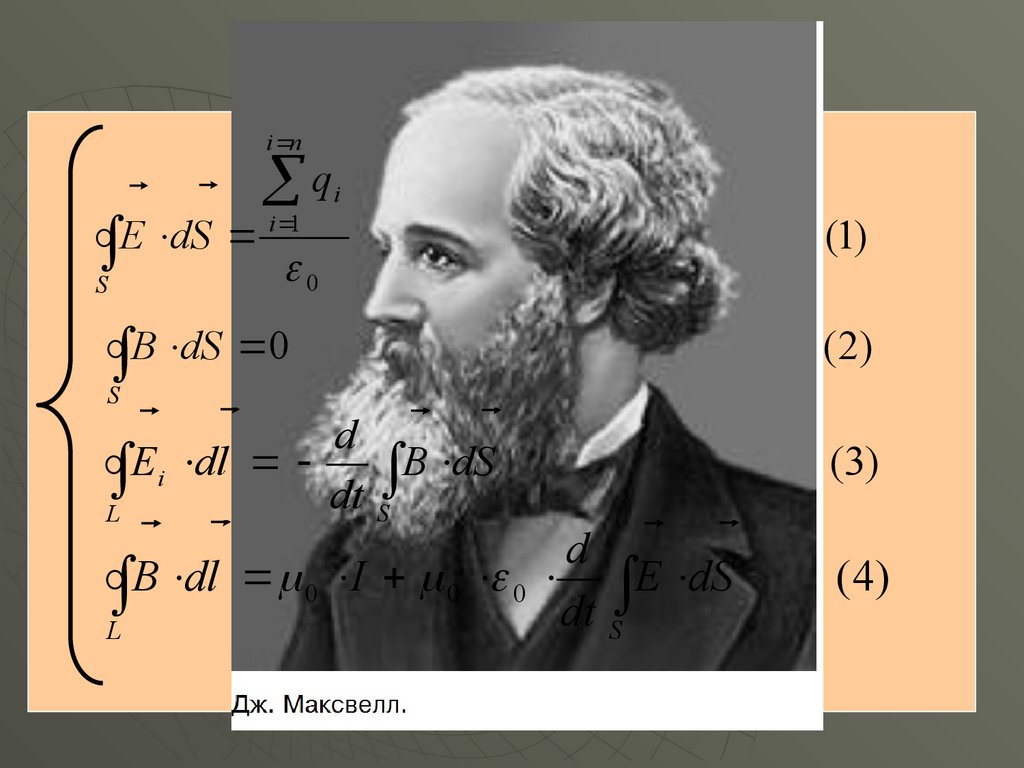

 Физика
Физика








