Похожие презентации:
Алгебраическая дробь и её основное свойство. 7 класс
1.
Алгебраическая дробь и еёосновное свойство
2.
«Человек подобен дроби, числитель есть то, что онесть, а знаменатель – то, что он о себе думает. Чем
больше знаменатель, тем меньше дробь.»
Лев Николаевич Толстой.
«Без знаний дробей никто не может
признаваться знающим арифметику».
Марк Тулий Цицерон
3.
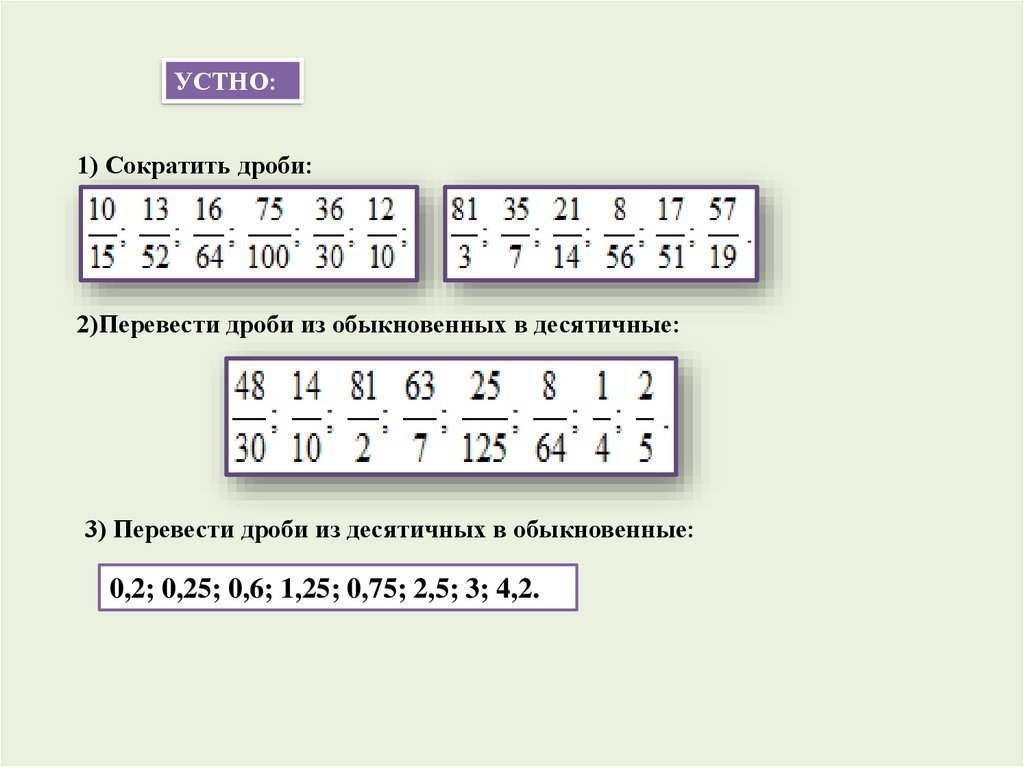
УСТНО:1) Сократить дроби:
2)Перевести дроби из обыкновенных в десятичные:
3) Перевести дроби из десятичных в обыкновенные:
0,2; 0,25; 0,6; 1,25; 0,75; 2,5; 3; 4,2.
4. Умножить числитель и знаменатель дроби на 2…
Умножить числитель изнаменатель дроби на 2…
1 3 5
; .
;
2 4 7
Разделите числитель знаменатель
дроби на 3…
9
15
;
18
33
.
4
5.
ПовторимЗначение обыкновенной дроби не изменится, если ее
числитель и знаменатель одновременно умножить или
разделить на одно и то же отличное от нуля число.
Пример 1:
3 12
4 16
(числитель и знаменатель
мы одновременно
умножили на одно и то же
число 4, значение
дроби не изменилось);
6.
Пример 2:22 2
33 3
(числитель и знаменатель мы
одновременно разделили на
одно и то же число 11, значение
дроби не изменилось).
7.
Основное свойство дробиПри умножении или делении числителя и знаменателя
алгебраической дроби на одно и то же число, не равное
нулю, получается равная ей дробь
Основное свойство дроби можно записать так:
а ma
,
b mb
b ≠ 0,
12 2
18 3
m ≠ 0,
ma а
.
mb b
a b c
a b d
c
.
d
8.
Над алгебраическими дробями можноосуществлять
преобразования аналогичные тем, которые вы
выполнили
для обыкновенной дроби.
Умножив числитель и знаменатель
алгебраического отношения на ненулевое
рациональное алгебраическое выражение,
получим алгебраическое отношение, равное
заданному на области допустимых значений
обоих алгебраических отношений.
2 2 5 10
;
3 3 5 15
2 а 2 a 5a
10a 4
;
3
3
3b 3b 5a
15ba
3
9.
Запомни!Основное свойство алгебраической дроби:
1. И числитель и знаменатель алгебраической дроби можно
умножить на один и тот же многочлен, на одно и тоже, отличное
от нуля число (тождественное преобразование алгебраической
дроби)
2. И числитель и знаменатель алгебраической дроби можно
разделить на один и тот же многочлен, на одно и тоже, отличное
от нуля число ( тождественное преобразование алгебраической
дроби – сокращение алгебраической дроби).
10.
a a;
b b
a
a
;
b
b
a
a
;
b a
a b
a
a
;
a b
a b
a b (b a )
b a
;
c d
c d
c d
a b
(a b)
a b
.
c d (d c )
d c
(a b) (b a ) ;
2
2
11.
Как используют основное свойство алгебраической дроби?Пример 1:
Преобразовать данные дроби так, чтобы получились дроби
с одинаковыми знаменателями.
2a 3b Решение:
и
3 5
Для этого найдем дополнительные множители для
каждой дроби. Это числа 5 и 3.
2a 2a 5 10 a
;
3
3 5
15
3b 3b 3 9b
;
5
5 3 15
5 – дополнительный множитель
3 – дополнительный множитель
12.
Пример 2:Преобразовать данные дроби так, чтобы получились дроби
с одинаковыми знаменателями.
2
a
a
и 3
2
4b 6 b
Решение:
Для этого найдем дополнительные множители для
каждой дроби. Это числа 3b и 2.
a
a 3b
3ab
2
;
2
3
4b
4b 3b 12b
a
a 2
2a
3
;
3
3
6b
6 b 2 12b
3b – дополнительный множитель
2 – дополнительный множитель
13.
Сократите данные дроби:1
1
1
2
12 а b x 6 2 a a b x 2a x
а)
;
2 2
2
2
18 a b y
6 3 a b y
3y
4
2
1
2
2
2
1
1
1
2
3x y 6 x y
3 x y( 1 2 y ) ( 1 2 y )
.
б) 3
2
2 2
3 x y 12 x y
3 x1 y( x 4 y ) ( x 4 y )
2
2
2
14.
Сократите дробь:4 а х 4 ах
в) 3
2 2
3
6 а х 12а х 6 ах
3
3
4 ах( a х )
2
2
6 ах( a 2ах х )
2
2
4 ах( a х )( a x )
2
6 ах( a х )
1
1
1
2 2 ах( a х )( a x ) 2( a x )
.
2 3 ах( a 1 х )( a x ) 3( a x )
1
1
15.
Восстановите, частичностёртые записи:
3
...
60а в
2
3 2
5а в 10а в
...
5 4
16.
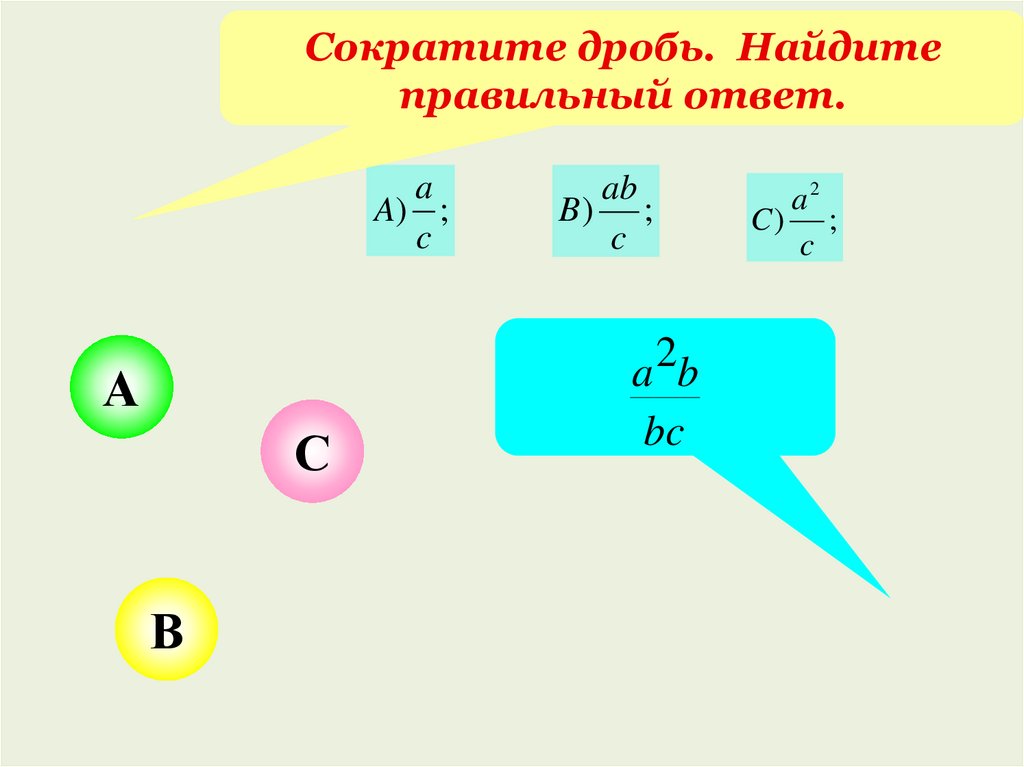
Сократите дробь. Найдитеправильный ответ.
a
A) ;
c
А
С
В
ab
B) ;
c
a 2b
bc
a2
C) ;
c
17.
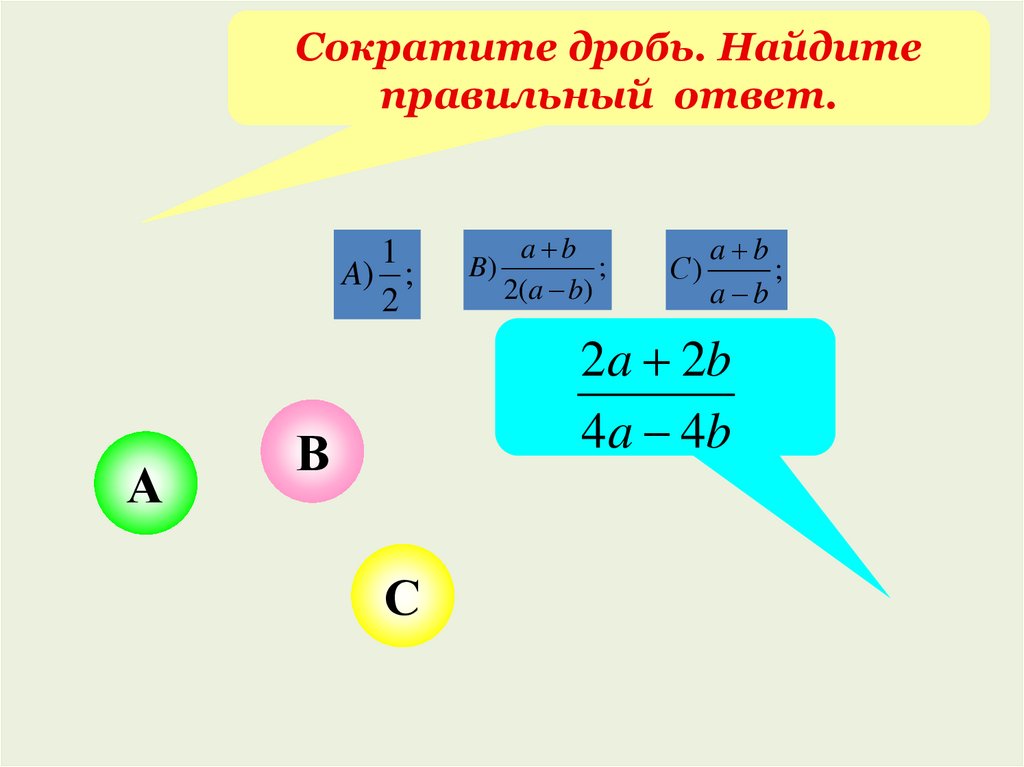
Сократите дробь. Найдитеправильный ответ.
1
A) ;
2
А
B)
a b
;
2(a b)
a b
С)
;
a b
2a 2b
4a 4b
В
С
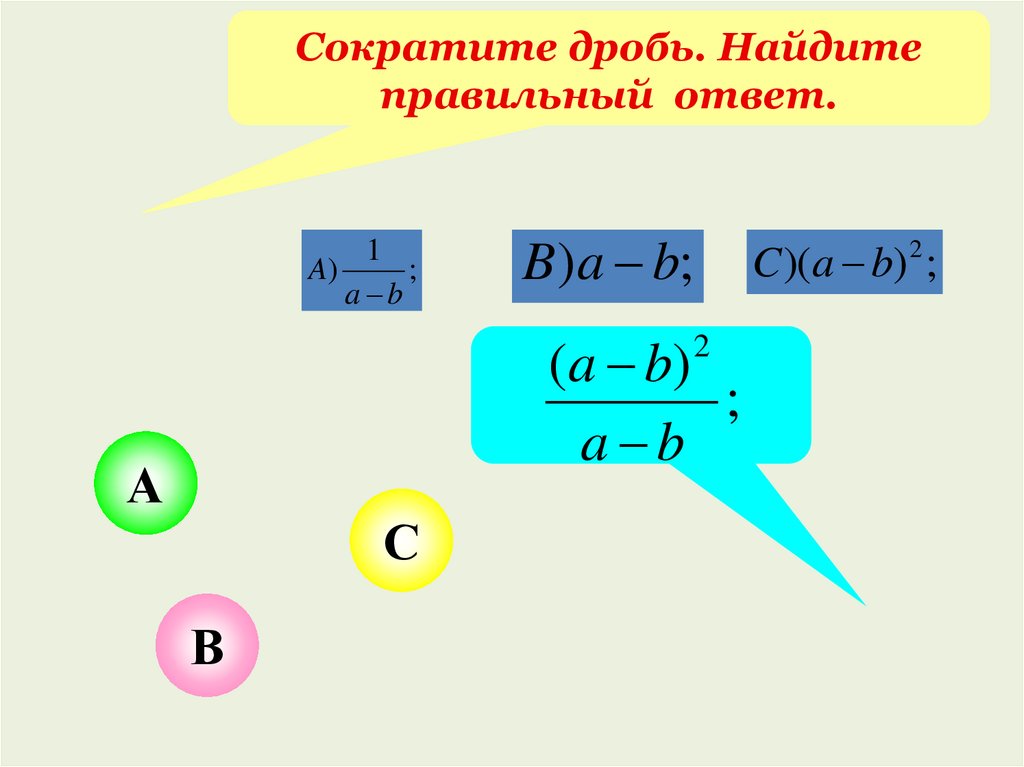
18.
Сократите дробь. Найдитеправильный ответ.
1
A)
;
a b
B )a b;
( a b)
;
a b
2
А
С
В
C )(a b) 2 ;
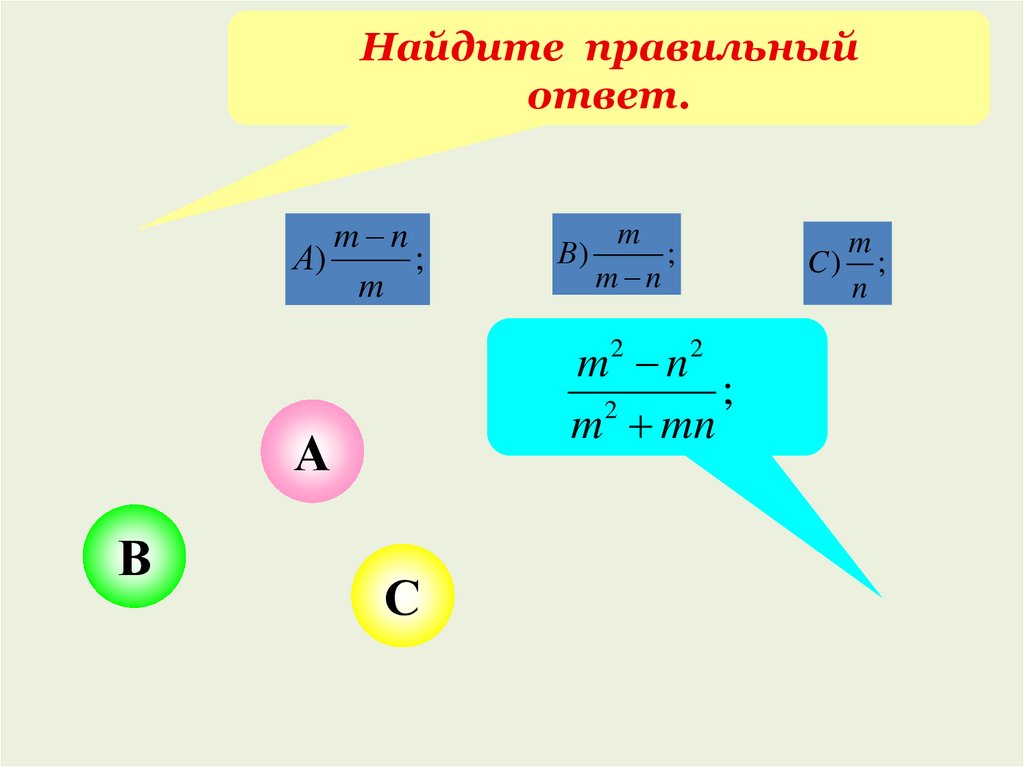
19.
Найдите правильныйответ.
m n
А)
;
m
m
В)
;
m n
m n
;
2
m mn
2
А
В
m
C) ;
n
С
2
20.
•Назовите основное свойство алгебраической дроби;•Как изменяются знаки у числителя и
знаменателя алгебраической дроби (следствие из основного свойства
дроби)?
21.
Учебные заданияСократите дробь
Сократите дробь












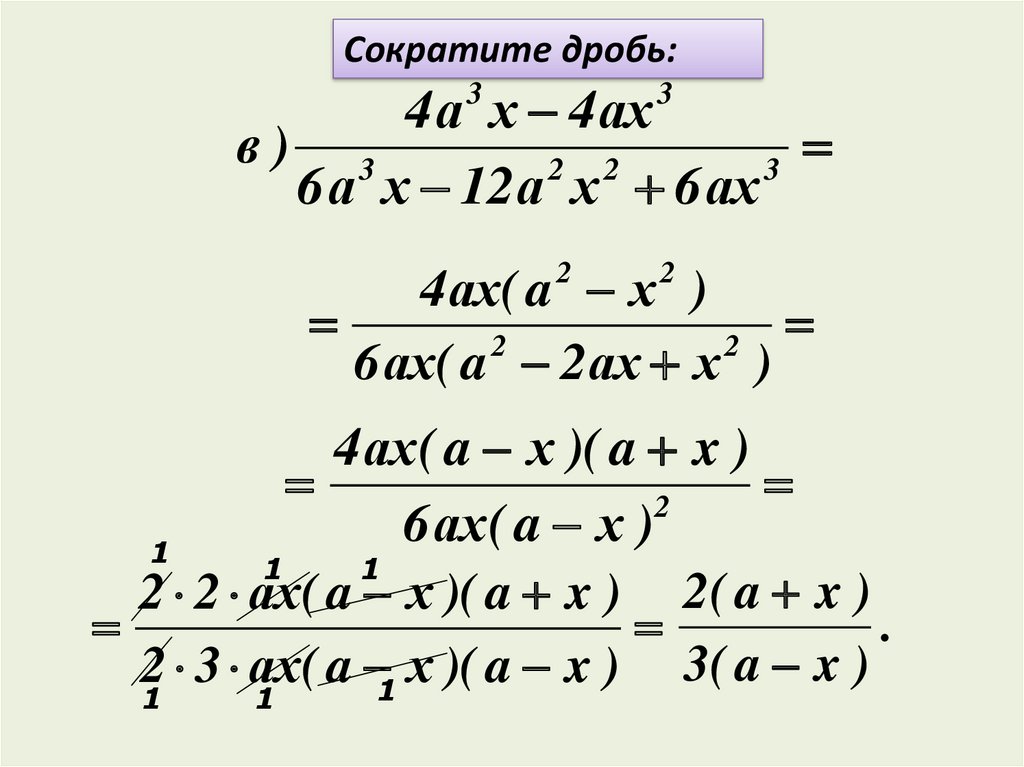



 Математика
Математика








