А.В. Бурдаков. Физика плазмы

1. А.В.Бурдаков.Физика плазмы.

Физика плазмы
Александр Владимирович Бурдаков
ИЯФ СО РАН, т.39-46-02
Спецкурс для магистрантов НГУ
Литература
http://www.inp.nsk.su/chairs/plasma/sk/fpl.ru.shtml

2.

А.В.Бурдаков.Физика плазмы.
Программа и вопросы
1. Понятие плазмы. Энергетическая единица измерения температуры-эВ. Квазинейтральность.
Дебаевская экранировка. Радиус Дебая. Потенциал пробной частицы в плазме.
Сравнение с кулоновским потенциалом.
Плазменные колебания. Характерный временной масштаб разделения зарядов. Плазменная частота.
Классическая и вырожденная плазма. Идеальная и неидеальная плазма.
Число частиц в дебаевской сфере. Влияние этого параметра на свойства плазмы.
Сравнение свойств плазмы, газа, твердого тела.
Характерные параметры лабораторной и космической плазмы.
2. Элементарные процессы в плазме. Ионизация и рекомбинация, основные процессы.
Корональное равновесие. Перезарядка, применение для диагностики и нагрева плазмы.
Степень ионизации. Формула Саха. Термодинамическое равновесие, ЛТР.
Зависимость степени ионизации от параметров плазмы, от потенциала ионизации.
3. Столкновения частиц в плазме. Кулоновский логарифм. Транспортное (кулоновское) сечение,
зависимость от энергии и заряда. Сила на неподвижный рассеивающий центр.
Кулоновский логарифм для плазмы и газа. Траектории частиц в плазме и газе.
Излучение из плазмы. Тормозное и рекомбинационное: характерные
зависимости от параметров плазмы, спектр (максимум в зависимости от температуры, ширина).
Линейчатое: интенсивность линии, отношение интенсивностей линий; доплеровское уширение,
штарковское расщепление, использование этих эффектов в диагностике плазмы.
Циклотронное излучение: частота, запирание излучения, интенсивность излучения черного тела.

3.

3.Релаксация импульса и энергии частиц в плазме.
Характерное время потери направленного импульса для холодной и горячей плазмы,
отличия в зависимости от скорости частицы. Сравнение времен релаксации электронной компоненты,
ионной компоненты и времени выравнивания электронной и ионной температур.
Проводимость плазмы, поле Драйсера, убегающие электроны.
4. Теоретические модели, используемые при исследовании плазмы.
Кинетическое уравнение с самосогласованным полем.
Функция распределения, выражение параметров плазмы через нее.
Физический смысл кинетического уравнения. Коэффициенты электропроводности и
теплопроводности плазмы, их зависимость от температуры (плотности).
5. Магнитная гидродинамика. МГД-приближение. Макроскопические характеристики плазмы.
Одножидкостая МГД, уравнения непрерывности, движения, теплопереноса,
сокращенные уравнения Максвелла. Вмороженность силовых линий магнитного поля.
6. Волны в плазме. МГД-волны, альфвеновская волна. Звуковые волны.
7. Ленгмюровская волна. Затухание Ландау.
Электромагнитные электронные волны. Прохождение электромагнитной волны через плазму:
зависимость показателя преломления от частоты, критическая плотность, интерферометрия плазмы.
Понятие о плазменных неустойчивостях.
8. Движение частиц в магнитных полях. Циклотронный резонанс. Дрейфовое движение.
Электрический, центробежный и градиентный дрейф.адиабатические инварианты.
Дрейфовое движение в тороиде. Движение заряженной частицы в открытой ловушке

4.

9. Управляемый термоядерный синтез. Проблемы энергетики. Радиационная опасность.
Основы термоядерного синтеза. Энергия связи. Сечения реакций. Критерий Лоусона.
10. Инерциальное удержание. Термоядерная бомба. Лазерные системы. Быстрый поджиг.
Сжатие рентгеновским излучением.
11. Магнитное удержание. Замкнутые системы. Токамак. Стелларатор. МГД неустойчивость.
Перспективы систем с магнитным удержанием.
Пинч. Тета-пинч.
12. Открытые магнитные ловушки. Пробкотрон.
Неустойчивости. Тандем. Термобарьер. Амбиполярная ловушка. Газодинамическая ловушка.
Многопробочная ловушка.
13. Низкотемпературная плазма и плазменный разряд. Понятие о Таундсеновской теории пробоя.
Кривая Пашена.
14. Плазменные технологии. Принцип работы плазменного дисплея, плазменного двигателя.
15. Плазма в космосе

5. А.В.Бурдаков.Физика плазмы.

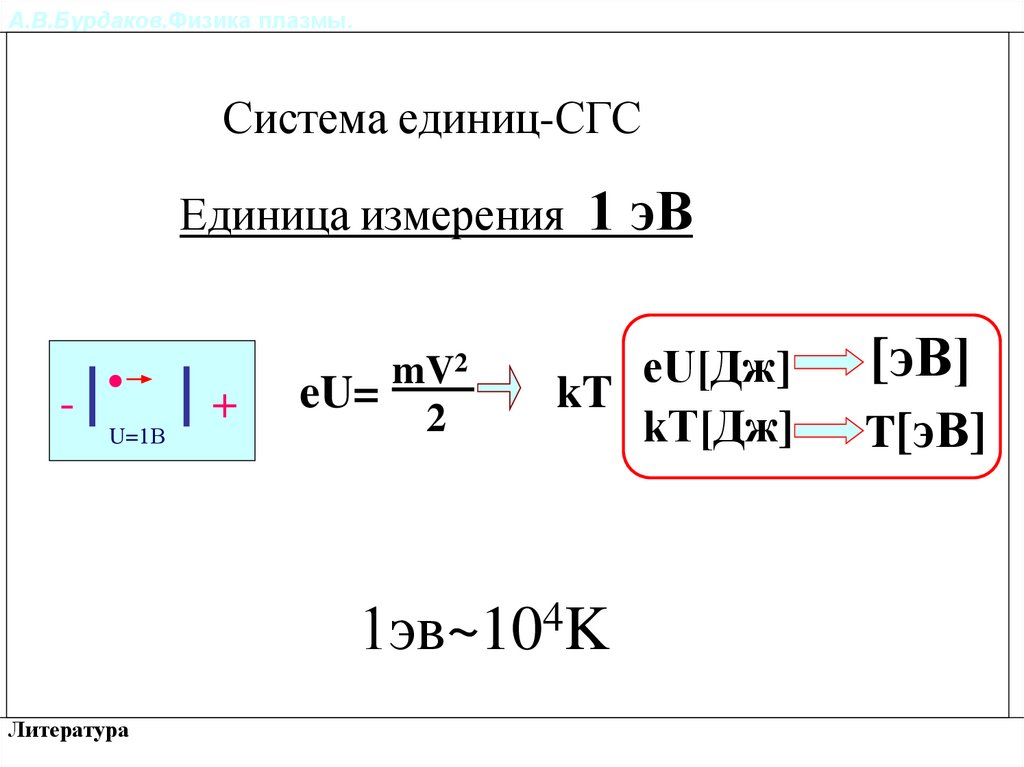
Система единиц-СГС
Единица измерения
-
+
U=1В
mV2
eU=
2
1 эВ
eU[Дж]
kT
kT[Дж]
4
1эв~10 K
Литература
[эВ]
T[эВ]

6. А.В.Бурдаков.Физика плазмы.

Классическая и вырожденная плазма.
Определения:
Плотность:
Температура:
Классическая и вырожденная плазма.
«Квантовый» масштабдлина волны Де-Бройля
«Плазменный» масштабрасстояние между частицами
Классическая плазма:
Литература

7. А.В.Бурдаков.Физика плазмы.

Литература
Классическая и вырожденная плазма.

8. А.В.Бурдаков.Физика плазмы.

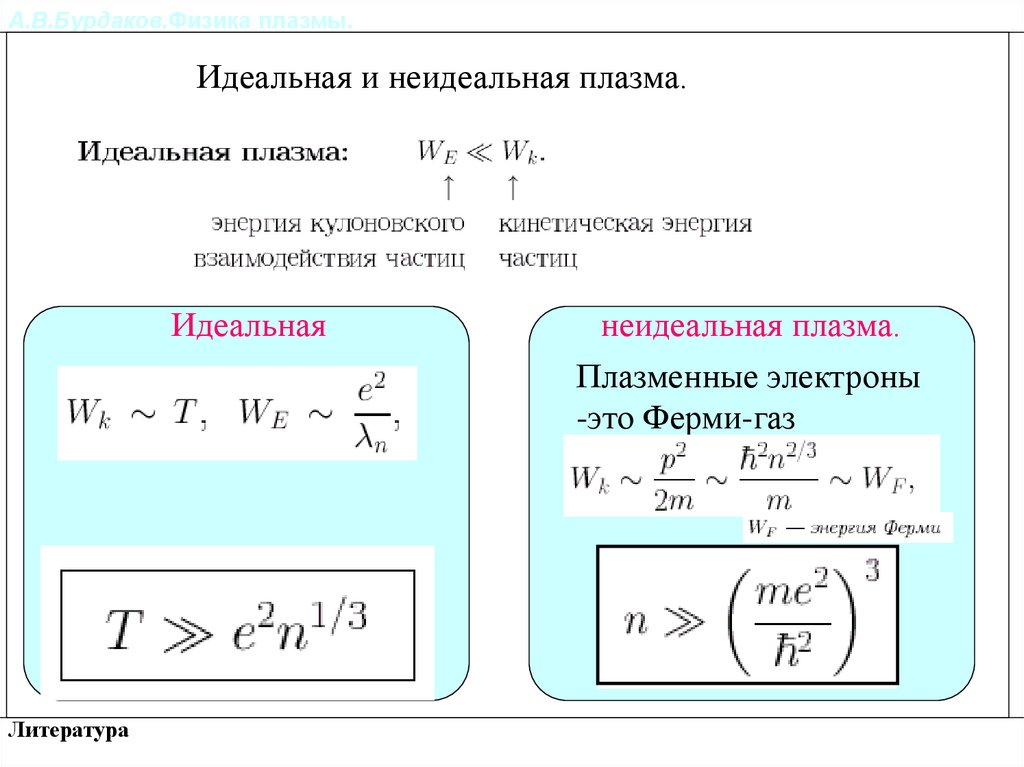
Идеальная и неидеальная плазма.
Идеальная и неидеальная плазма.
Идеальная
неидеальная плазма.
Плазменные электроны
-это Ферми-газ
Литература

9. А.В.Бурдаков.Физика плазмы.

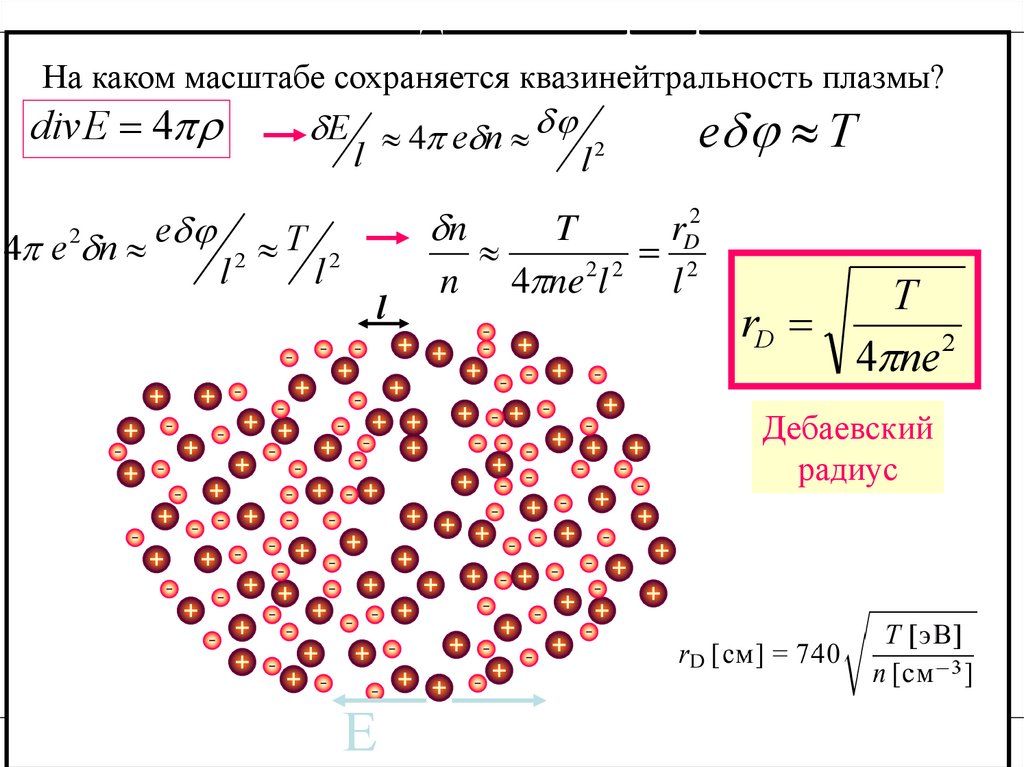
Дебаевская экранировка
На
каком масштабе сохраняется квазинейтральность плазмы?
А.В.Бурдаков.Физика плазмы.
divE 4
4 e n e
2
l
E 4 e n
l
2
T
l
2
e T
n
l2
l
T
rD2
2
2 2
n 4 ne l
l
T
rD
2
4 ne
Дебаевский
радиус
Литература
Е

10. А.В.Бурдаков.Физика плазмы.

Плазменные колебания
Макроскопическое отклонение от квазинейтральности
ведет к появлению электрического поля.
Для плоского слоя плазмы:
x
-смещение электронов
m x eEx 4 ne 2 x
Ленгмюровские колебания
Плазменная частота
Литература
4 ne
p
m
2

11. А.В.Бурдаков.Физика плазмы.

Дебаевская экранировка
Дебаевская экранировка
Уравнение
Пуассона
4
q r rD
e
r
Литература

12. А.В.Бурдаков.Физика плазмы.

Литература
Параметр неидеальности

13.

А.В.Бурдаков.Физика плазмы.
Корональное равновесие
ev
ni
na
Литература

14.

А.В.Бурдаков.Физика плазмы.
Литература
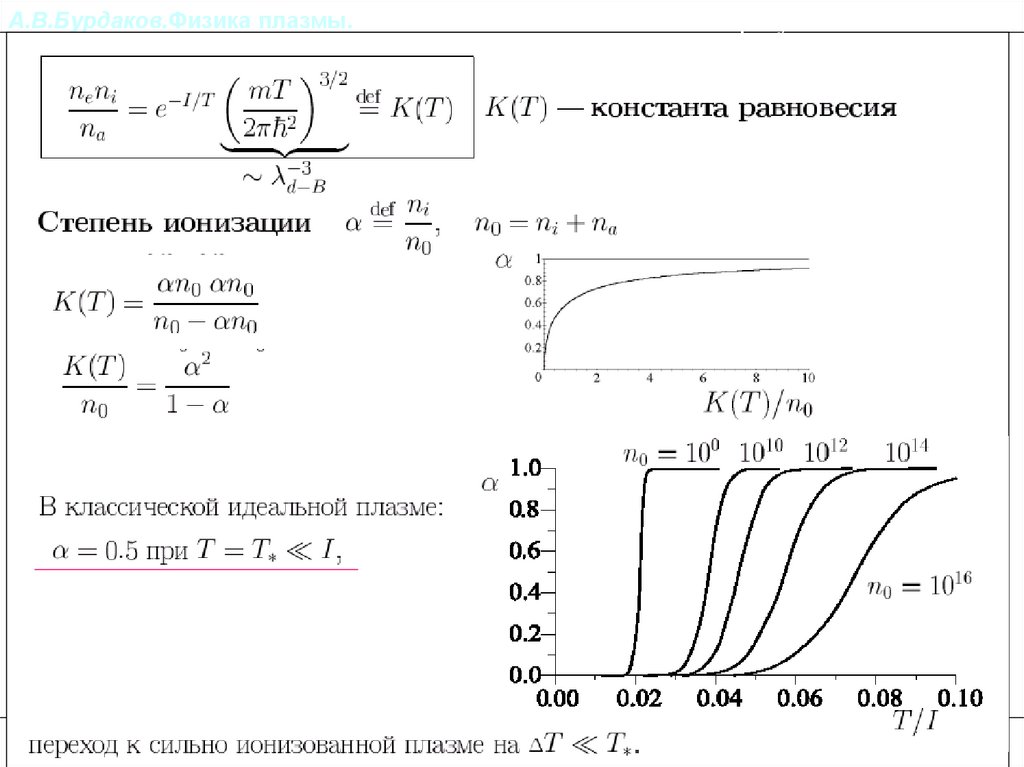
Степень ионизации. Формула Саха

15.

А.В.Бурдаков.Физика плазмы.
Литература
Степень ионизации. Формула Саха

16.

А.В.Бурдаков.Физика плазмы.
Литература
Степень ионизации. Формула Саха

17.

А.В.Бурдаков.Физика плазмы.
Литература
Степень ионизации. Формула Саха

18.

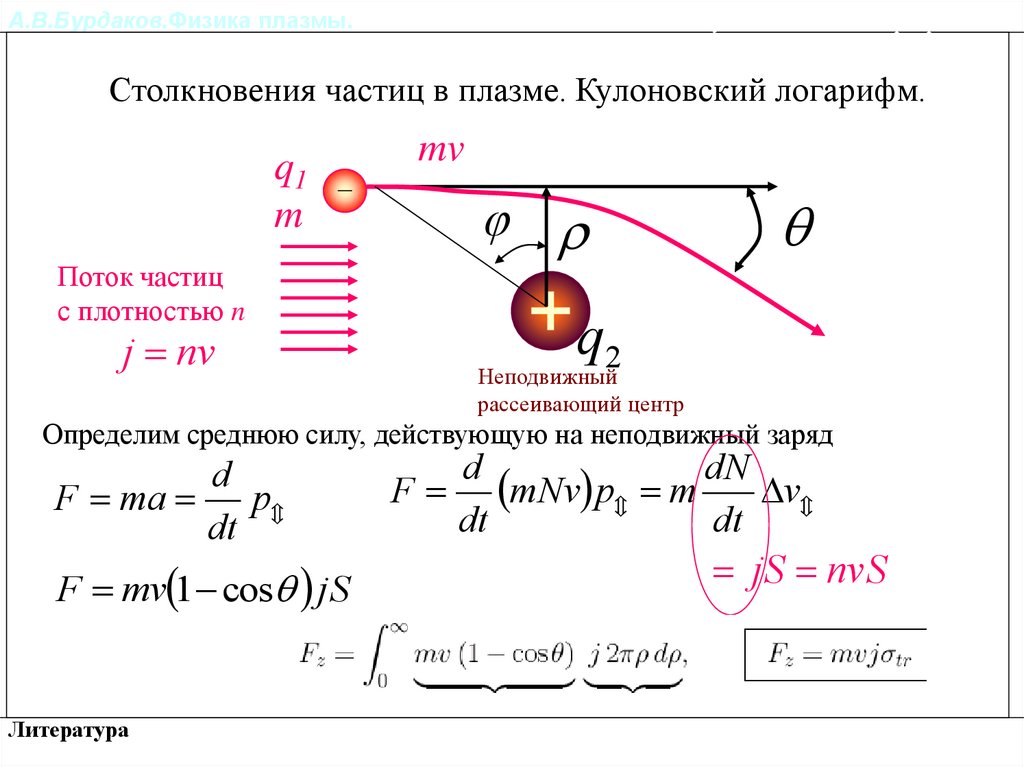
А.В.Бурдаков.Физика плазмы.Столкновения частиц в плазме. Кулоновский логарифм.
Столкновения частиц в плазме. Кулоновский логарифм.
q1
m
Поток частиц
с плотностью n
j nv
mv
q2
Неподвижный
рассеивающий центр
Определим среднюю силу, действующую на неподвижный заряд
d
F ma
p
dt
d
dN
F mNv p m
v
dt
dt
F mv 1 cos jS
Литература
Ландау, Лифшиц. Механика, §19
jS nvS

19.

А.В.Бурдаков.Физика плазмы.Столкновения частиц в плазме. Кулоновский логарифм.
(dt dz d tg )
v
v
Ср. точная формула Резерфорда:
Литература

20.

А.В.Бурдаков.Физика плазмы.Столкновения частиц в плазме. Кулоновский логарифм.
Литература

21.

А.В.Бурдаков.Физика плазмы.Столкновения частиц в плазме. Кулоновский логарифм.
Литература

22.

А.В.Бурдаков.Физика плазмы.
Релаксация импульса и энергии частиц в плазме.
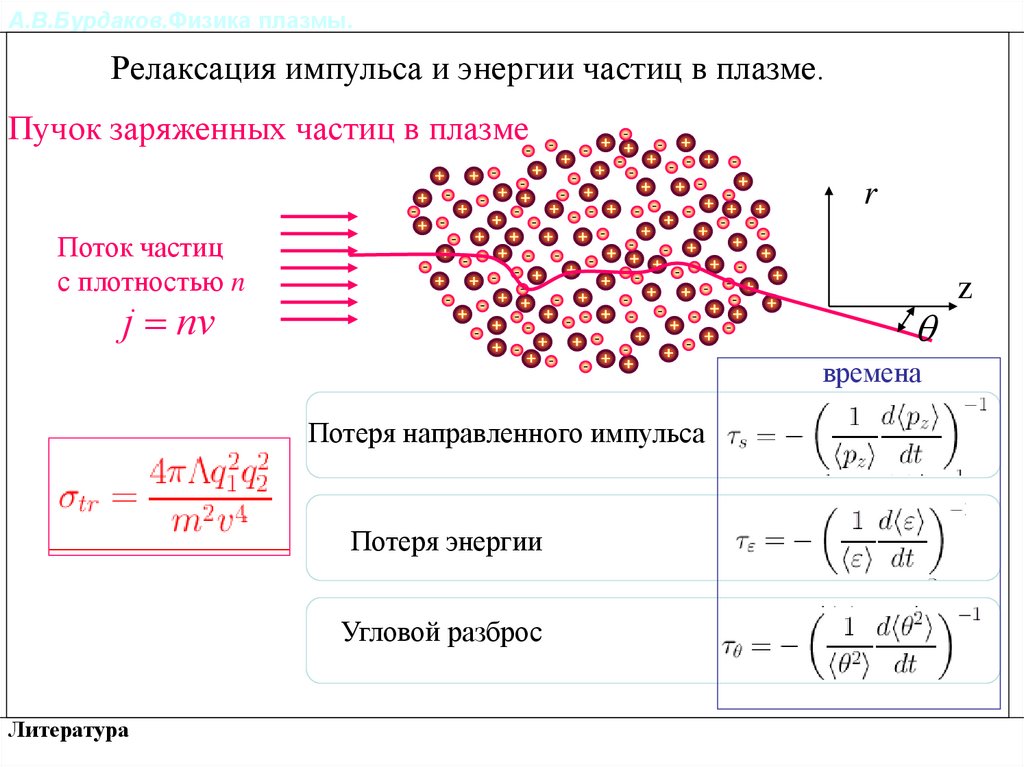
Релаксация импульса и энергии частиц в плазме.
Пучок заряженных частиц в плазме
r
Поток частиц
с плотностью n
j nv
времена
Потеря направленного импульса
Потеря энергии
Угловой разброс
Литература
http://www.inp.nsk.su/chairs/plasma/sk/fpl.ru.shtml
z

23.

А.В.Бурдаков.Физика плазмы.
Литература
Релаксация импульса и энергии частиц в плазме.

24.

А.В.Бурдаков.Физика плазмы.
Литература
Релаксация импульса и энергии частиц в плазме.

25.

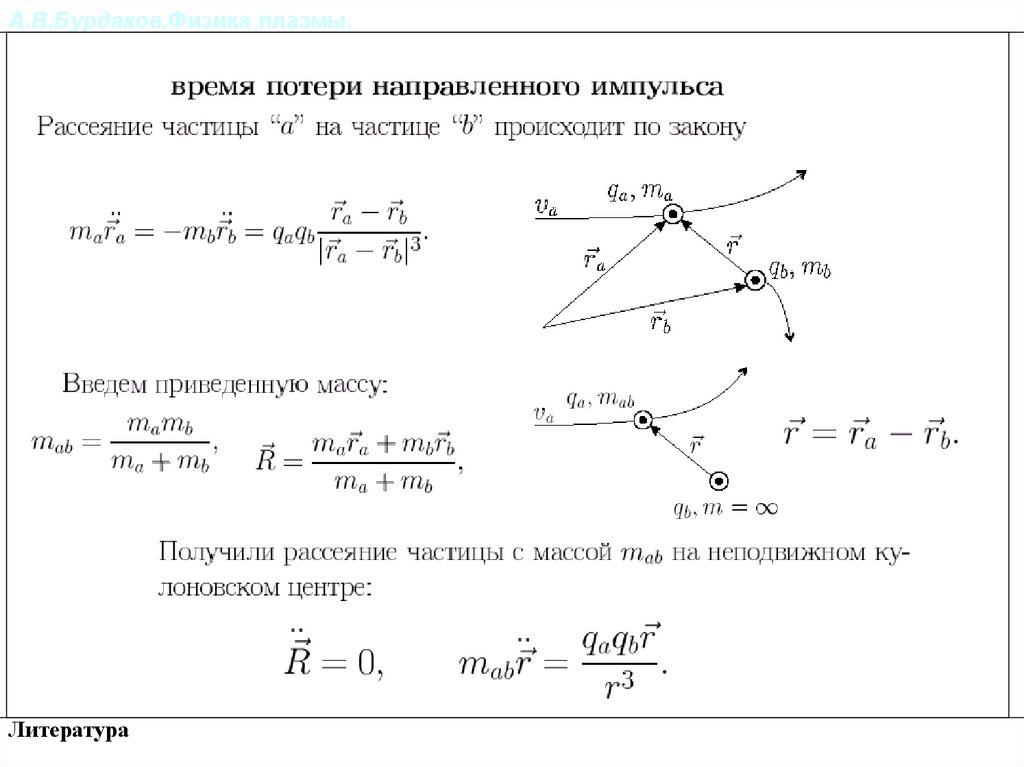
А.В.Бурдаков.Физика плазмы.
Релаксация импульса и энергии частиц в плазме.
a
Литература

26.

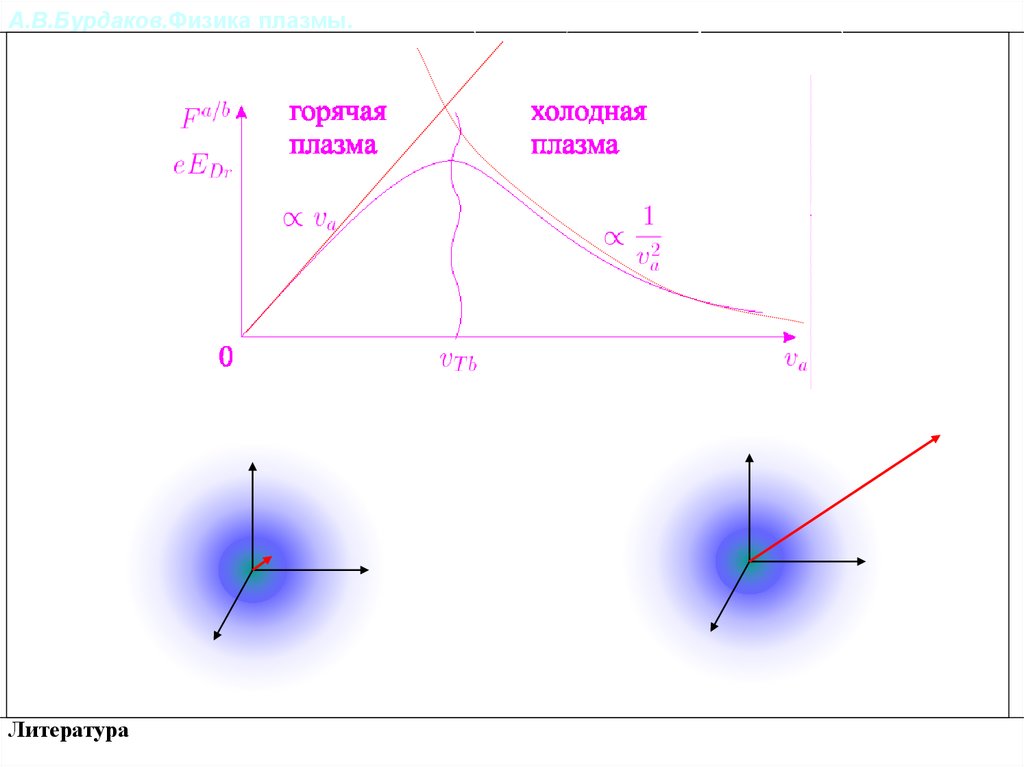
А.В.Бурдаков.Физика плазмы.
Релаксация импульса и энергии частиц в плазме.
, тогда
Плазма «горячая»
va
F
a
b
4 qa2 qb2
mab
F
Литература
a
b
f vb d vb
0
va2
va
4 qa2 qb2
va
va
mab
4 qa2 qb2
4 v a
f 0
mab
3
f 0 4 vb2 dvb
0
va2
va
va

27.

А.В.Бурдаков.Физика плазмы.
Литература
Релаксация импульса и энергии частиц в плазме.

28.

А.В.Бурдаков.Физика плазмы.
Литература
Релаксация импульса и энергии частиц в плазме.

29.

А.В.Бурдаков.Физика плазмы.
Литература
Релаксация импульса и энергии частиц в плазме.

30.

А.В.Бурдаков.Физика плазмы.
Релаксация импульса и энергии частиц в плазме.
получим времена
Литература
релаксации:

31.

А.В.Бурдаков.Физика плазмы.
Релаксация импульса и энергии частиц в плазме.
Длина свободного пробега
Частота столкновений
В водородной плазме
Литература

32.

А.В.Бурдаков.Физика плазмы.Излучение из плазмы.
Излучение из плазмы.
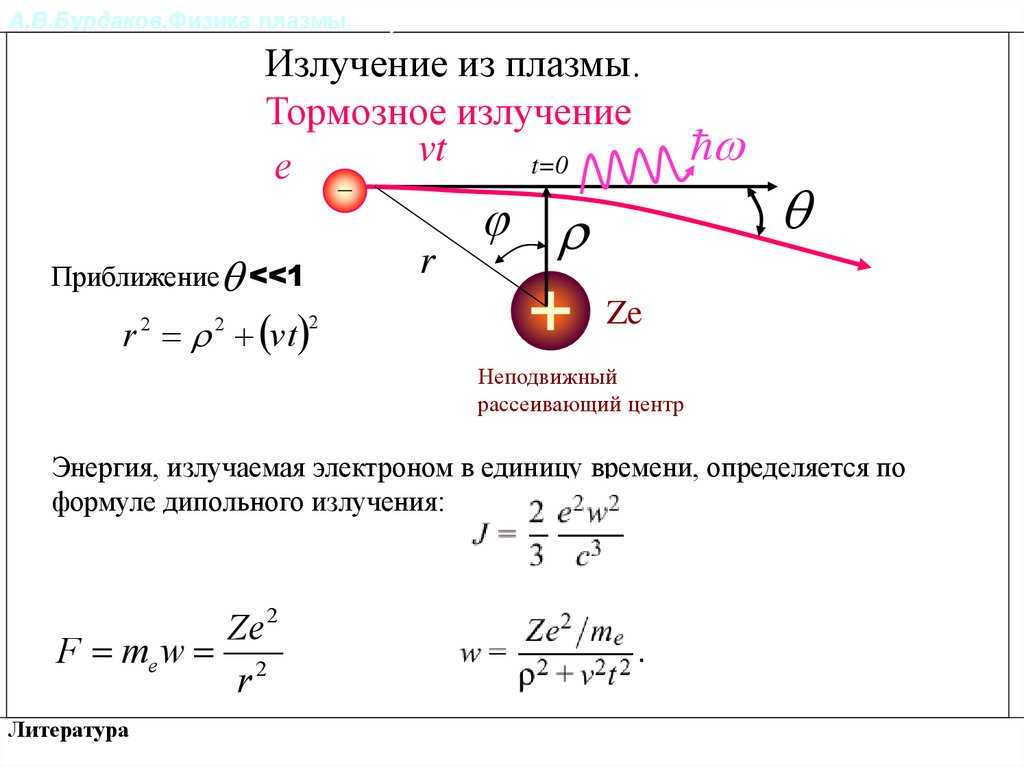
Тормозное излучение
vt
t=0
е
r
Приближение <<1
Ze
r 2 2 vt
2
Неподвижный
рассеивающий центр
Энергия, излучаемая электроном в единицу времени, определяется по
формуле дипольного излучения:
Ze 2
F me w 2
r
Литература
Ландау, Лифшиц. Механика, §19

33.

А.В.Бурдаков.Физика плазмы.Излучение из плазмы.
Тормозное излучение
Мощность излучения:
Энергия, излучаемая за один пролет:
Если :Поток частиц с плотностью ne и скоростью v :
Интеграл формально расходится на нижнем пределе, но
me v 2
2
Литература
, тогда
Б
me v

34.

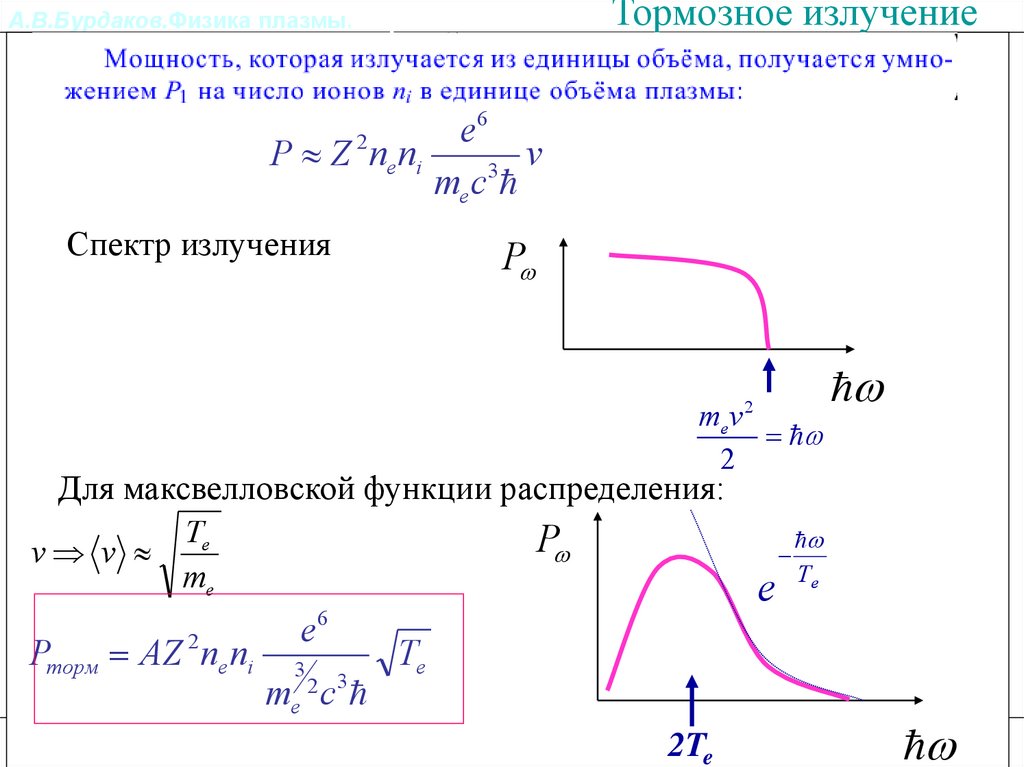
А.В.Бурдаков.Физика плазмы.Излучение из плазмы.
Тормозное излучение
6
e
P Z 2 ne ni
v
3
me c
Спектр излучения
P
2
me v
2
Для максвелловской функции распределения:
v v
Te
me
Pторм AZ 2 ne ni
Литература
P
e6
3
me 2 c 3
e
Te
Te
2Te

35.

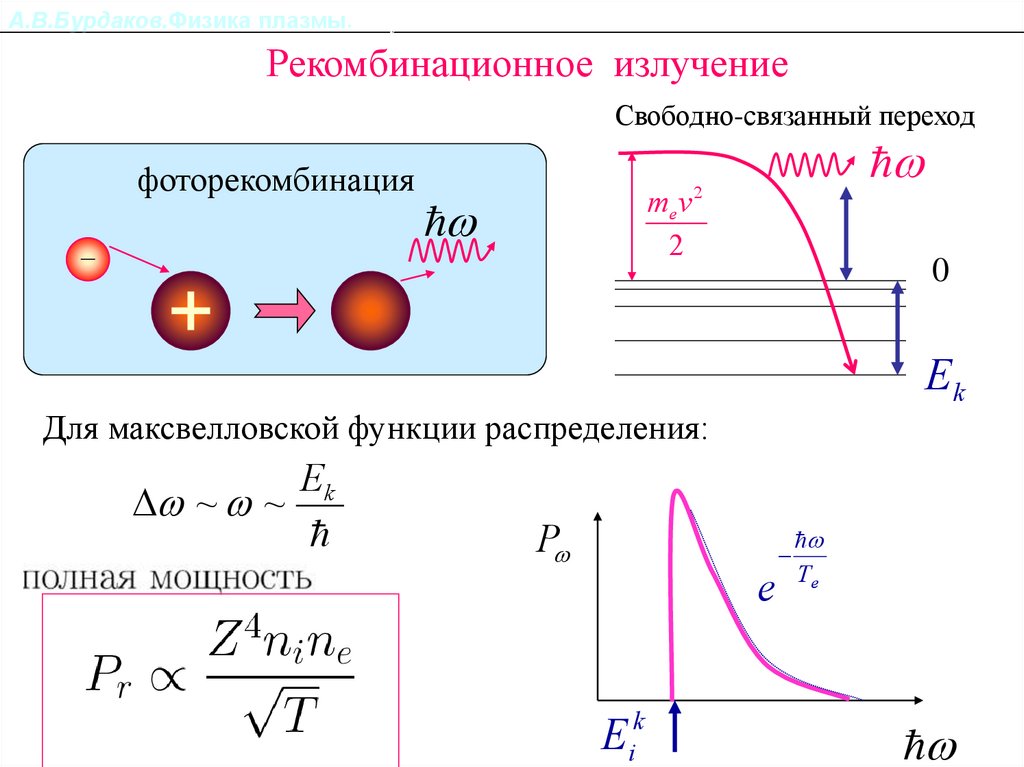
А.В.Бурдаков.Физика плазмы.Излучение из плазмы.
Рекомбинационное излучение
Свободно-связанный переход
фоторекомбинация
me v 2
2
0
Ek
Для максвелловской функции распределения:
Ek
~ ~
P
e
Eik
Te

36.

А.В.Бурдаков.Физика плазмы.Излучение из плазмы.
Линейчатое излучение
Связанно-связанный переход
Интенсивность линии
E
gk
k
I I d
Aki
nle T
4
U
0
Ek
Отношение интенсивностей линий одного и того же иона
I1
A1 g1 1 E1 E2 T
e
I 2 A2 g 2 2

37.

А.В.Бурдаков.Физика плазмы.Излучение из плазмы.
Линейчатое излучение
Уширение (ресщепление) линий
Доплер-эффект
kv
v -скорость
vk
c
Штарк -эффект
Для водорода и водородоподобных ионов (He+, Li++….):
3
s
ks E
2me
Зееман-эффект
eB
z
gz
2me c

38.

А.В.Бурдаков.Физика плазмы.Излучение из плазмы.
Линейчатое излучение
Доплер-эффект
kv
vk
c
В плазме:
Для максвелловской функции распределения:
J
2
1
exp
2
0
0
0
c
vT
c
2T
Ma
Гауссов профиль

39.

Линейчатое излучение
А.В.Бурдаков.Физика плазмы.Излучение из плазмы.
Штарк -эффект
Для водорода и водородоподобных ионов (He+, Li++….):
3
s
ks E
2me
H
В плазме:
Микрополе:
1
3
~ e
~
E ~ 2 , r n , E 2.6en
r
Имеет распределение-уширение линий
В движении:
1
E E vB
c
2
3

40.

А.В.Бурдаков.Физика плазмы.Излучение из плазмы.
Циклотронное излучение
Мощность излучения определяется по формуле дипольного излучения:
где

41.

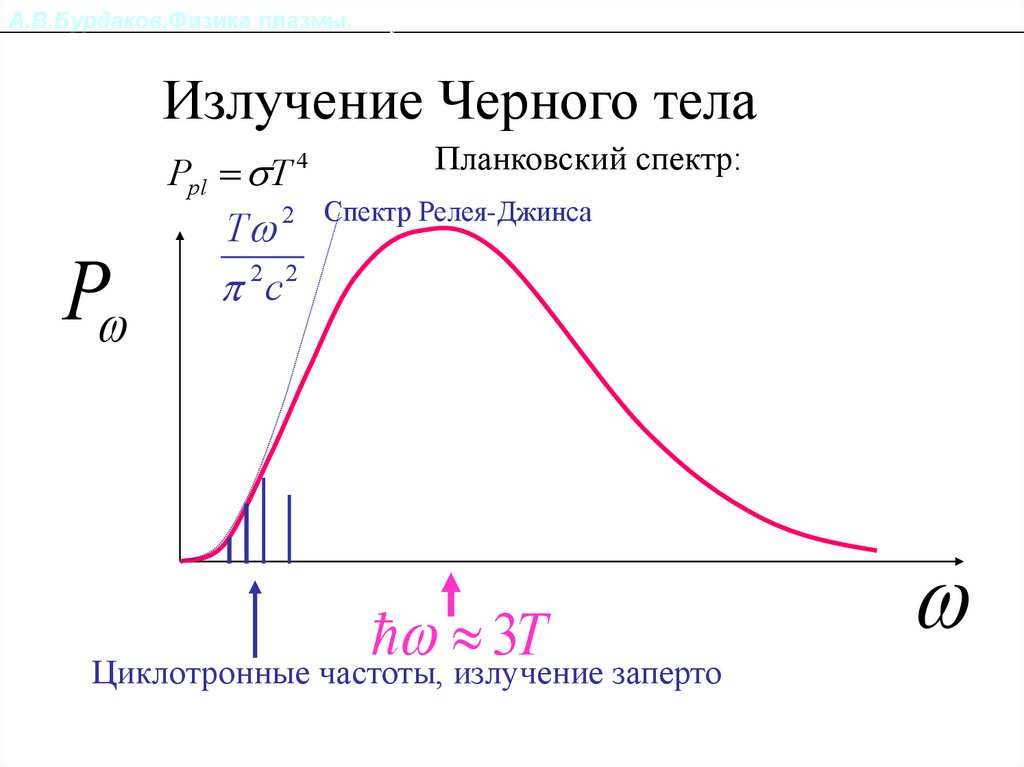
А.В.Бурдаков.Физика плазмы.Излучение из плазмы.
Излучение Черного тела
Ppl T 4
P
T 2
2c 2
Планковский спектр:
Спектр Релея-Джинса
3
T
Циклотронные частоты, излучение заперто

42.

А.В.Бурдаков.Физика плазмы. Кинетическое уравнение
Формула для электропроводности
Формула для электропроводности
Используем кинетическое уравнение
Водородная плазма: e, i
Stei
f0 f
ei
Кинетическое уравнение для этой задачи имеет вид:
f0 f
eE f
me V
ei
Пусть f f 0 f1
Пренебрегаем произведением малых сомножителей
Тогда:
eE f 0 f1
me V ei
eE f1
me V

43.

А.В.Бурдаков.Физика плазмы. Кинетическое уравнение
Формула для электропроводности
Отсюда:
e E
ne 2
ei f 0 dV
ei E
j e Vf1 V dV
me
me
2
Ранее получали:
Смысл приближения слабого электрического поля:
Условие
f1 f 0
означает:
f 0
f0
eE f 0 f1
eE ei
~
1
me V ei
me VT
V VT
Или:
eE
ei 1
meTe
Энергия, приобретаемая электроном в электрическом поле на
длине св. пробега, должна быть намного меньше тепловой.

44.

А.В.Бурдаков.Физика плазмы. Кинетическое уравнение Коэффициент теплопроводности
Коэффициент теплопроводности
Стационарное состояние, поле отсутствует. Одномерный случай.
f0 f
f
v
x
Для
l ~ v L
x-направление градиента температуры
функцию распределения можно разложить
в ряд
по степеням малого параметра : f f 0 f1 ....
1
mv 2
m 2
f 0 n
exp
2 T
2T x
1
2
2
f 0
1
m mv
f1 v
n v 5 3
x
2 2
2T 2
2T
2
exp mv T
2T x

45.

А.В.Бурдаков.Физика плазмы. Кинетическое уравнение Коэффициент теплопроводности
Поток тепла:
mv2
mv2
mv2
q v
f v dv v
f 0 v dv v
f1 v dv
2
2
2
=0
Второй интеграл:
T T
T
q 3n
m x
x
3
2
5
T
Te
3
.
510
Коэффициент теплопроводности 3.2n e
ei
ei
Точное выражение:
n
m
Ток и тепло переносятся электронами
3
2
Te ,
5
2
e
T
и не зависят от плотности

46.

А.В.Бурдаков.Физика плазмы.
Одножидкостная магнитная гидродинамика
Уравнение непрерывности
Закон сохранения массы или числа частиц
Уравнение движения
Уравнение Ньютона, отнесенное к единичному объему среды
Уравнение теплопереноса
Уравнение адиабаты, сохранение энергии
После введения в уравнения обычной гидродинамики силы Лоренца
система уравнений оказалась незамкнутой. Она должна рассматриваться
совместно с уравнениями Максвелла.

47.

А.В.Бурдаков.Физика плазмы.
Одножидкостная магнитная гидродинамика
div B 0
1 B
rotE
c t
4 1 E
rotB
J
c
c t
Током смещения можно пренебречь
>>

48.

А.В.Бурдаков.Физика плазмы.
1 B
rotE
c t
Одножидкостная магнитная гидродинамика
4
rotB
J
c

49.

А.В.Бурдаков.Физика плазмы.
Одножидкостная магнитная гидродинамика

50.

А.В.Бурдаков.Физика плазмы.
Одножидкостная магнитная гидродинамика
силовая трубка
Силовые линии
1
Так как E 0 k 0 (ЭДС=0 на обходе «жидкого» контура К)
c
Откуда: k BdS 0
(k )

51.

А.В.Бурдаков.Физика плазмы.
Простейшие равновесные системы
Статическое равновесие: v 0, 0
t
1
p J B
c
Линии поля и линии тока лежат на одной поверхности: J p B p 0
Пусть магнитное поле имеет одну компоненту: B Bz
B2
B2
0 p
p
const
8
8
-пинч
Bz
Магнитное поле внутри плазмы равно 0,
давление=const, поле на границе:
Bz2
p
8
Плазма сжимается нарастающим магнитным полем

52.

А.В.Бурдаков.Физика плазмы.
Z-пинч
I
H
a
B 2 a
p 2nT
8
2I
На границе: B
ca
I 8c a nT
2
2
2
Для термоядерной плазмы : T=10 кэВ, n=41014см-3 I=1МА
Такая плазма равновесна, но неустойчива……….

53.

А.В.Бурдаков.Физика плазмы.
Классификация плазменных неустойчивостей

54.

А.В.Бурдаков.Физика плазмы.

55.

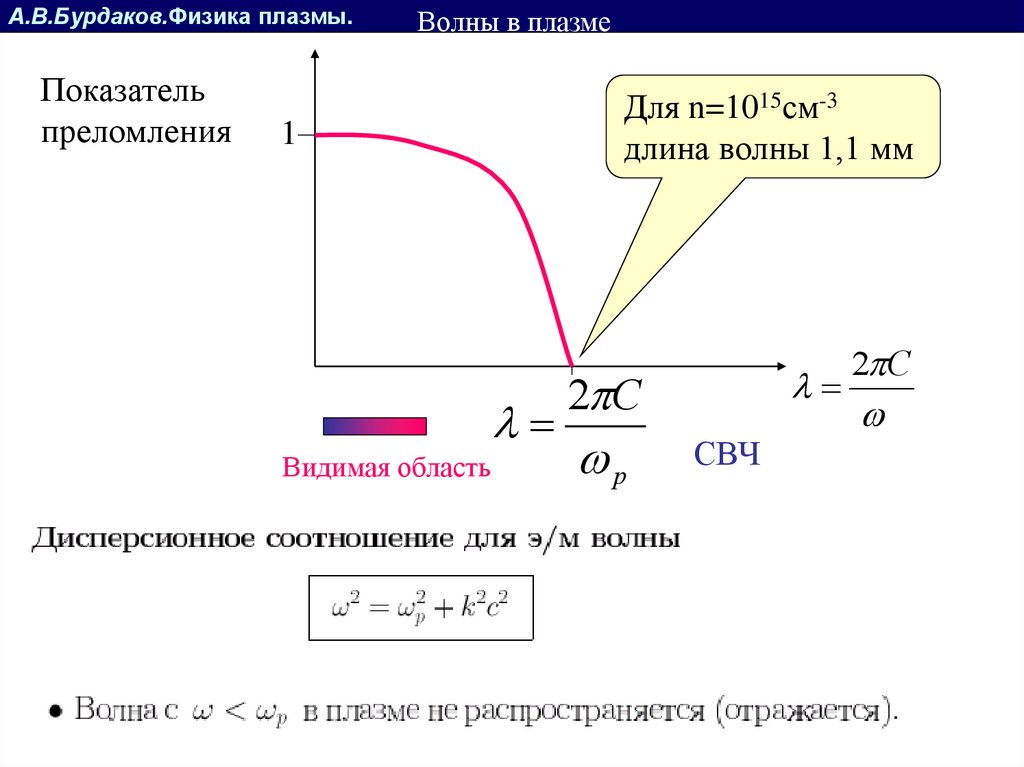
А.В.Бурдаков.Физика плазмы.
Показатель
преломления
Волны в плазме
Для n=1015см-3
длина волны 1,1 мм
1
Видимая область
2 C
p
СВЧ
2 C

56.

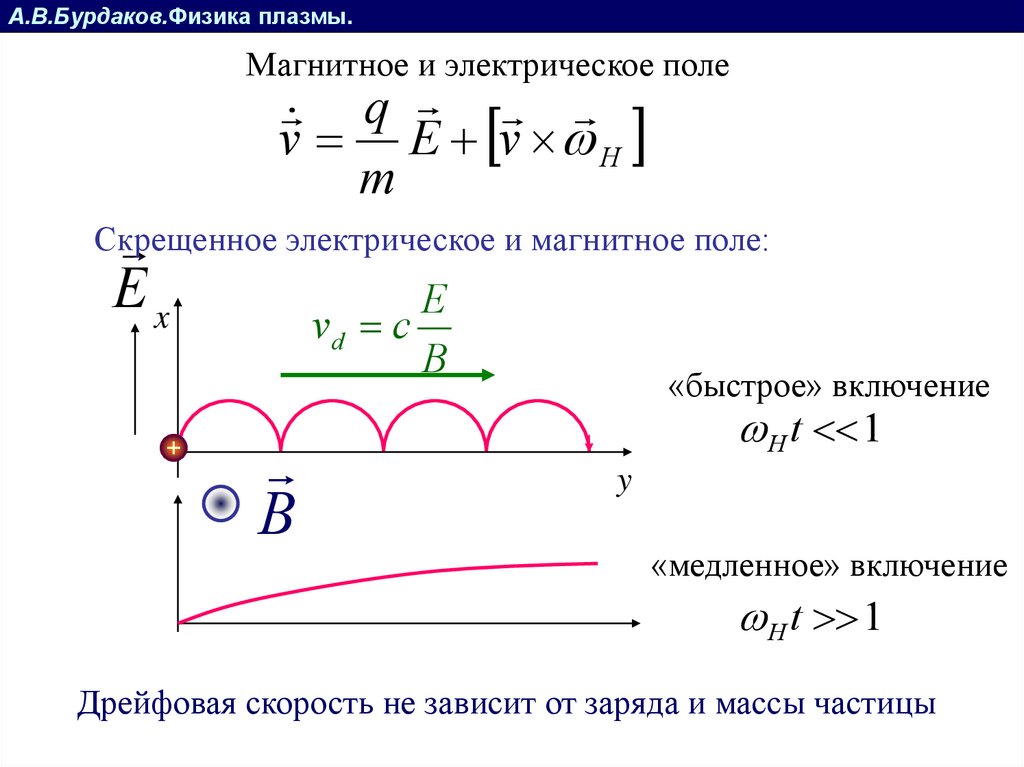
А.В.Бурдаков.Физика плазмы.
Магнитное и электрическое поле
q
v E v H
m
Ex
Скрещенное электрическое и магнитное поле:
E
vd c
B
B
«быстрое» включение
H t 1
y
«медленное» включение
H t 1
Дрейфовая скорость не зависит от заряда и массы частицы

57.

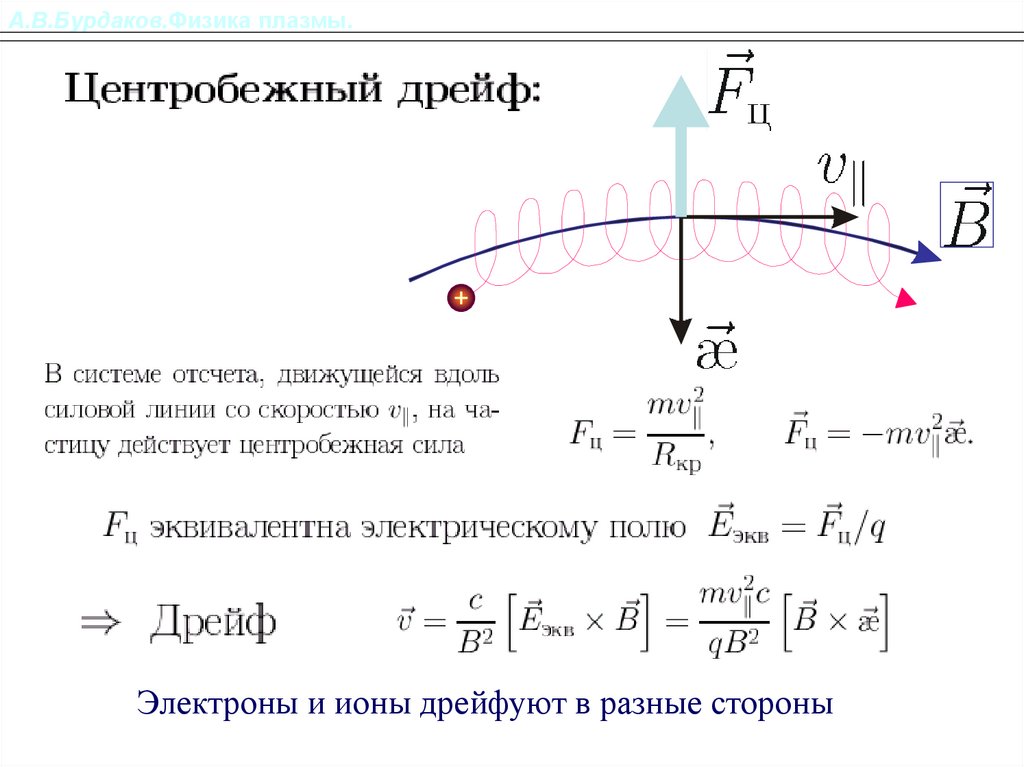
А.В.Бурдаков.Физика плазмы.
сильное поле, большая кривизна
слабое поле, малая кривизна
Электроны и ионы дрейфуют в разные стороны

58. А.В.Бурдаков.Физика плазмы.

Литература
Электроны и ионы дрейфуют в разные стороны

59.

А.В.Бурдаков.Физика плазмы.

60.

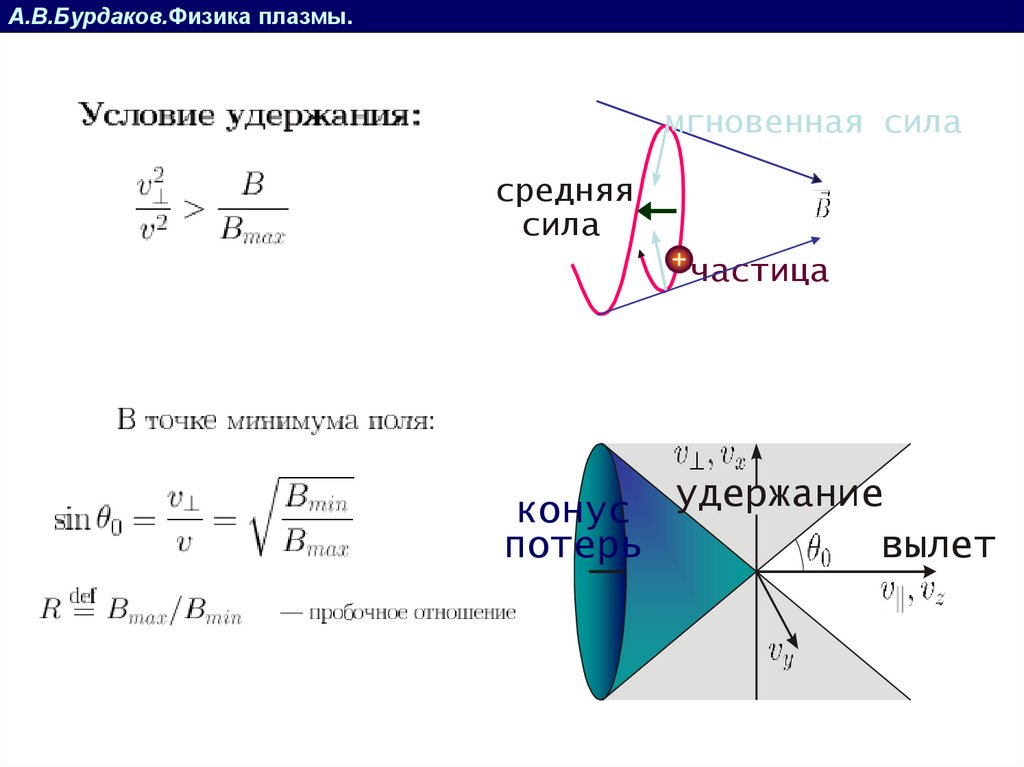
А.В.Бурдаков.Физика плазмы.
мгновенная сила
средняя
сила
частица
конус удержание
вылет
потерь

61. А.В.Бурдаков.Физика плазмы.

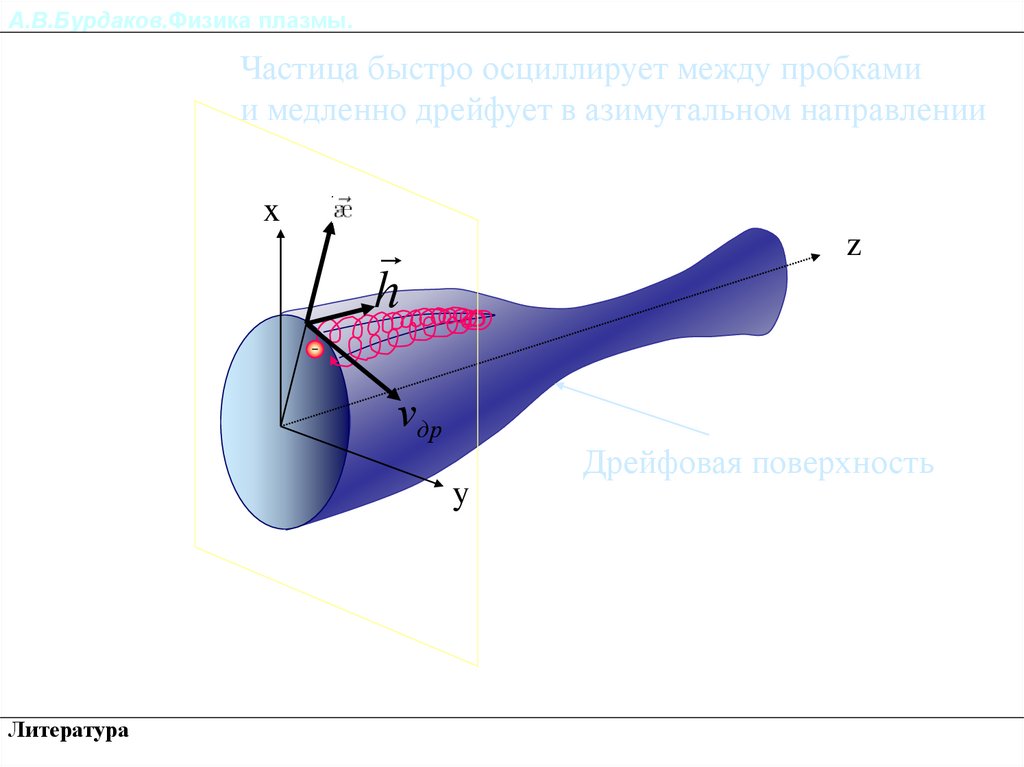
Частица быстро осциллирует между пробками
и медленно дрейфует в азимутальном направлении
x
h
z
vдр
y
Литература
Дрейфовая поверхность

62.

А.В.Бурдаков.Физика плазмы.
тороид
vдр
1
B
r
B
E
- -----
+ + ++ + +
E
+ + ++ + +
-----
B
Электроны и ионы дрейфуют в разные стороны
*поляризация плазмы
*в электрическом @ магнитном поле- плазма
дрейфует наружу тора
*в тороидальной геометрии плазму не удержать!
vдр

63.

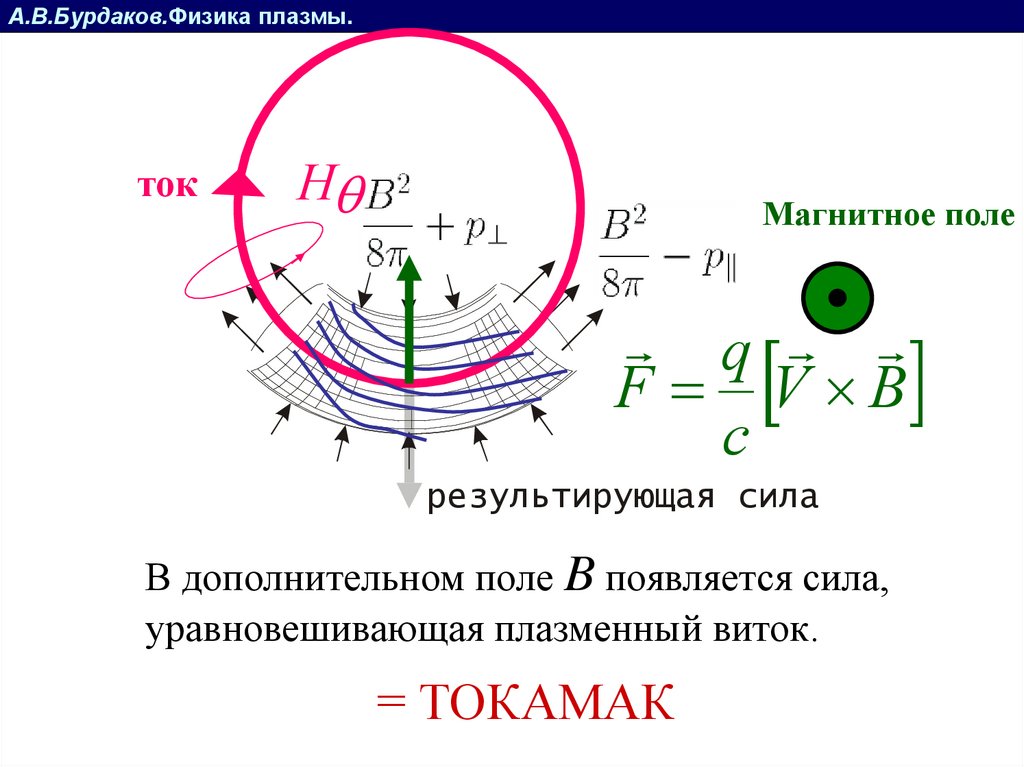
А.В.Бурдаков.Физика плазмы.
ток
H
Магнитное поле
q
F V B
c
результирующая сила
В дополнительном поле B появляется сила,
уравновешивающая плазменный виток.
= ТОКАМАК

64.

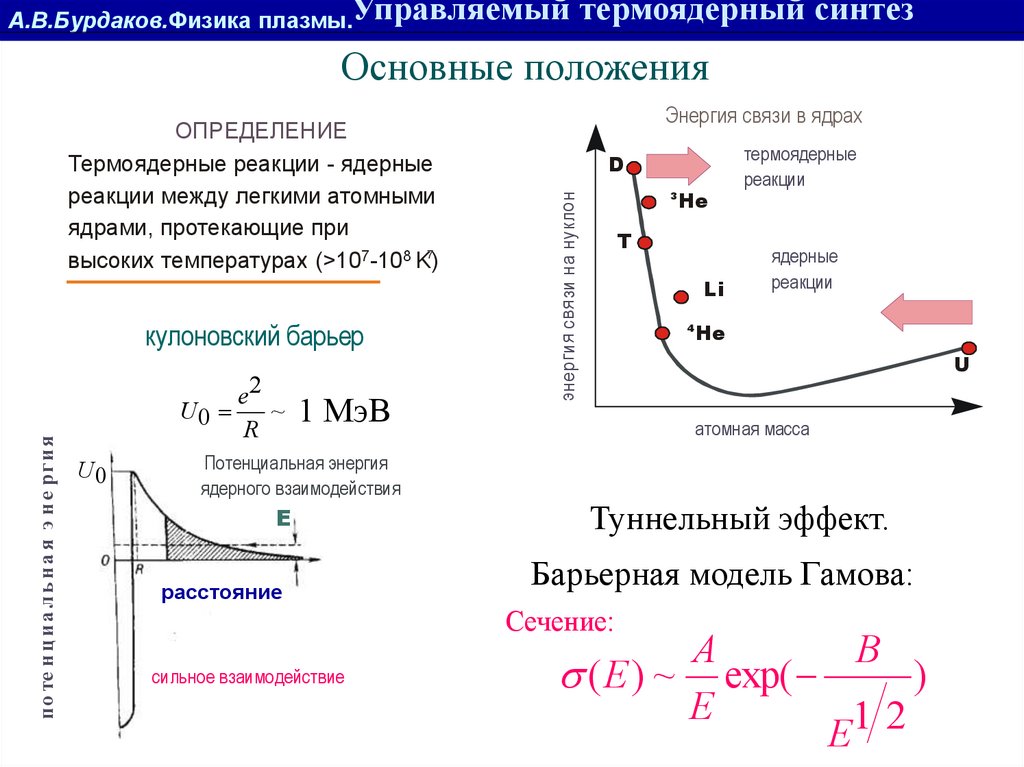
А.В.Бурдаков.Физика плазмы.Управляемый
термоядерный синтез
Основные положения
по те н ц иа л ьн а я э н е рги я
кулоновский барьер
e2
U0
~
R
U0
1 МэВ
Потенциальная энергия
ядерного взаимодействия
Е
расстояние
Энергия связи в ядрах
D
3
энергия связи на нуклон
ОПРЕДЕЛЕНИЕ
Термоядерные реакции - ядерные
реакции между легкими атомными
ядрами, протекающие при
высоких температурах (>107-108 K)7
T
Li
4
ядерные
реакции
He
U
атомная масса
Туннельный эффект.
Барьерная модель Гамова:
Сечение:
сильное взаимодействие
He
термоядерные
реакции
A
B
( E ) ~ exp(
)
E
1
2
E

65.

Критерий Лоусона
А.В.Бурдаков.Физика плазмы.
Реакция DT
Плазма с
nD nT
1
n
2
1 2
n v
4
Число реакций в единице объема в единицу времени:
Выделяемая мощность:
Pт ерм ояд
1 2
n v EDT
4
3nT
, (3nT 3 nTe 3 nTi )
Мощность потерь:
2
2
Условие положительного выхода
Критерий Лоусона:
n
(EDT=18МэВ)
Энергетическое
время жизни
3nT
Pт ерм ояд
12T
n
f T
v EDT
!!! В критерий Лоусона входит произведение

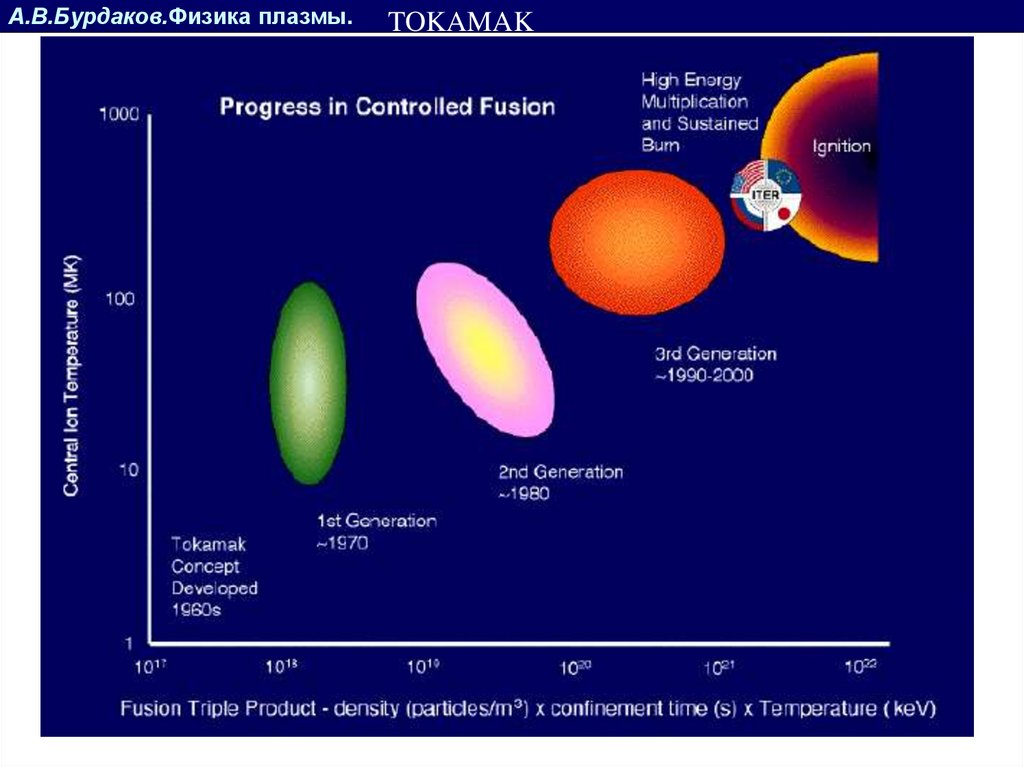
66.

А.В.Бурдаков.Физика плазмы.
n
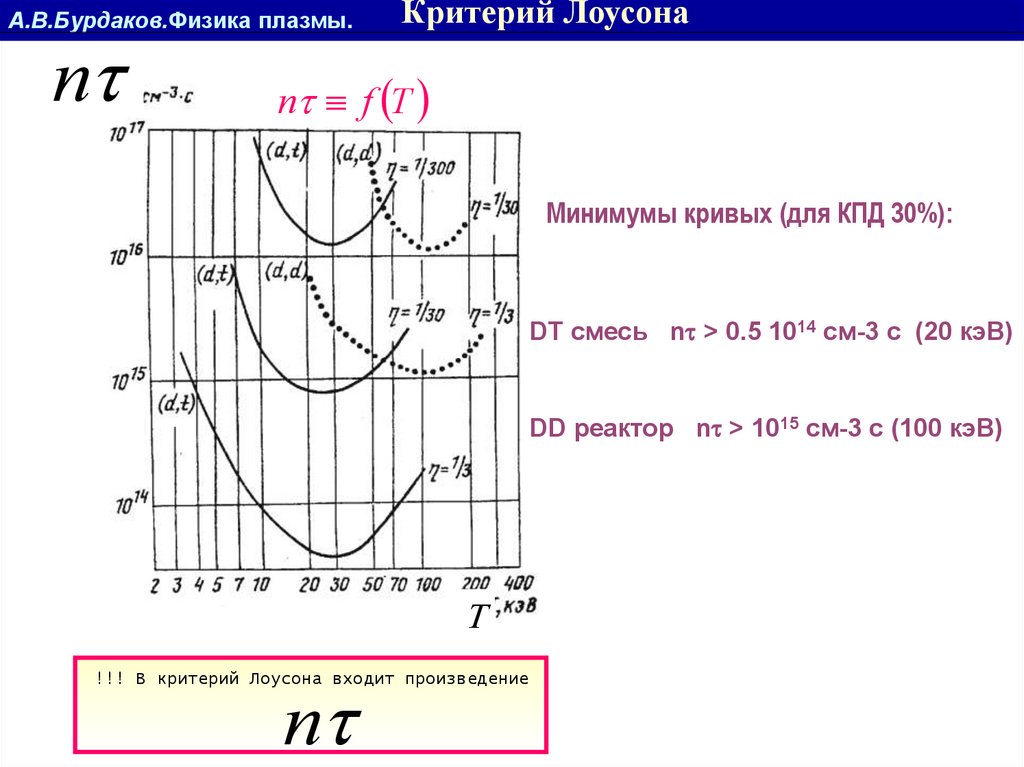
Критерий Лоусона
n f T
Минимумы кривых (для КПД 30%):
DT смесь n > 0.5 1014 см-3 с (20 кэВ)
DD реактор n > 1015 см-3 с (100 кэВ)
T
n
!!! В критерий Лоусона входит произведение

67.

А.В.Бурдаков.Физика плазмы.
Литература
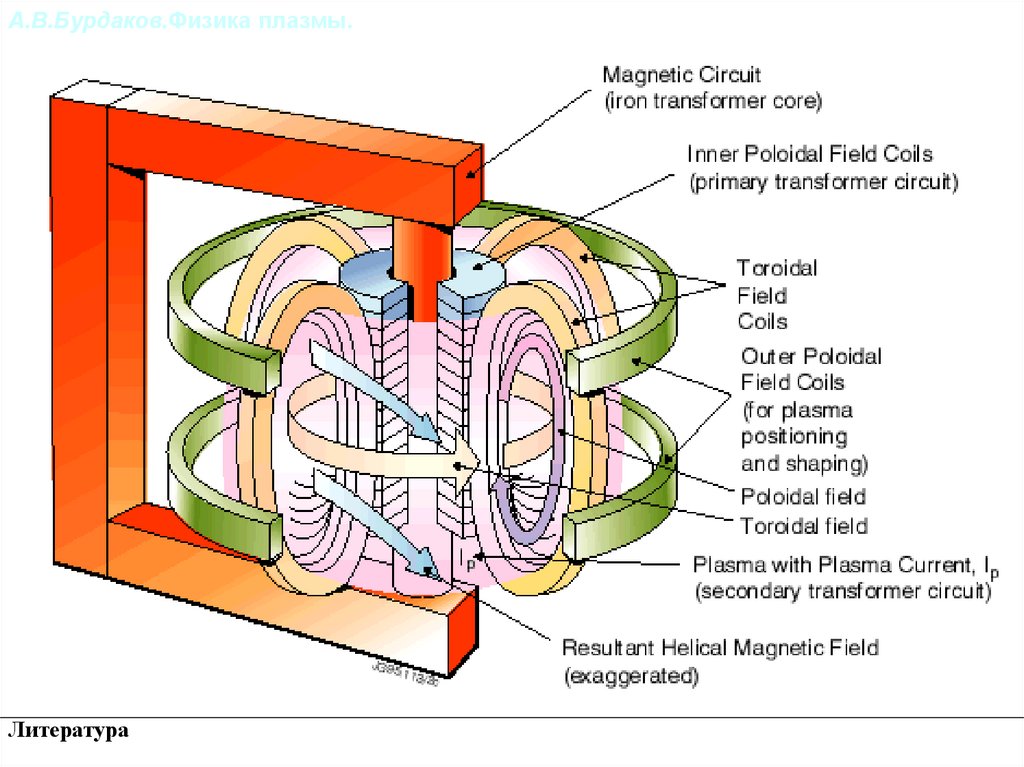
TOKAMAK

68. Понятие магнитной поверхности

В.В.Поступаев "Инженерно-физические проблемы УТС". Раздел 4. Магнитное удержание плазмы. Токамаки.
Понятие магнитной поверхности
и вращательного преобразования
* “вращательное преобразование“ - следствие наличия тока, текущего по плазме
* силовые линии незамкнуты и образуют магнитную поверхность
* магнитные поверхности являются вложенными
* условие равновесия плазмы P = [jB] означает, что магнитные поверхности
есть поверхности постоянного давления (B P = 0) и на них располагаются
линии тока (j P = 0)
* через каждую точку проходит только одна поверхность (в вырожденных системах
без вращательного преобразования - множество)
* магнитные поверхности разрушаются турбулентностью
* предельная величина плазменного тока (критерий Шафранова-Крускала)
r B (r)
(более точно q(r) = -- --------- > 1
интегрирование по
R B ( r)
всей поверхности)
q(r) - запас устойчивости, при q < 1 развивается винтовая МГД-неустойчивость
(выброс плазмы на стенку)
* величина q изменяется по малому радиусу, т.е. шаг “кручения”
соседних магнитных поверхностей разный q’ = dq/dr - shear
При увеличении тока в плазме растет ее нагрев, увеличивается давление,
но одновременно приближается порог винтовой МГД-неустойчивости

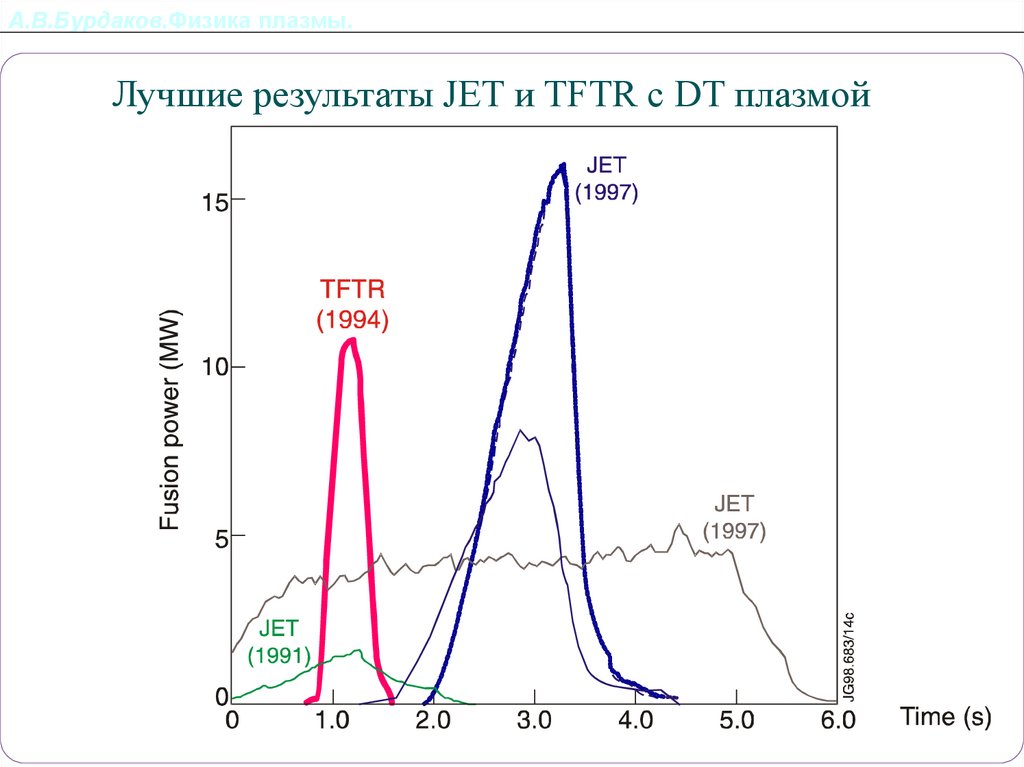
69. А.В.Бурдаков.Физика плазмы.

TOKAMAK
Лучшие результаты JET и TFTR с DT плазмой

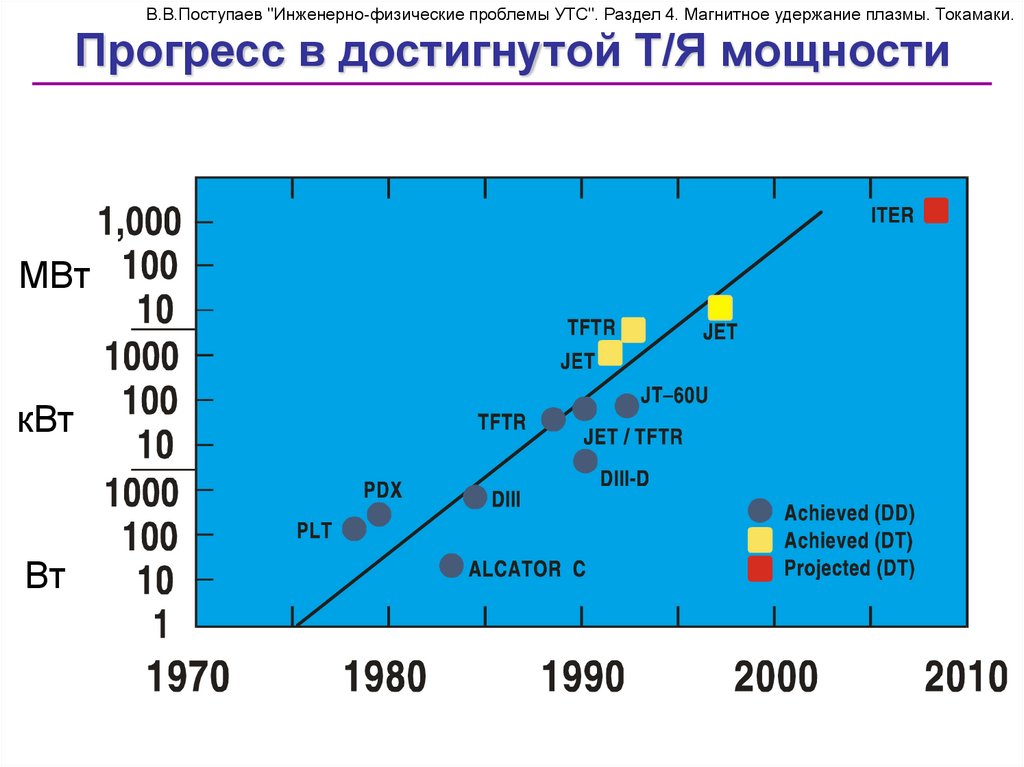
70. Прогресс в достигнутой Т/Я мощности

В.В.Поступаев "Инженерно-физические проблемы УТС". Раздел 4. Магнитное удержание плазмы. Токамаки.
Прогресс в достигнутой Т/Я мощности
МВт
кВт
Вт

71.

А.В.Бурдаков.Физика плазмы.
TOKAMAK

72. А.В.Бурдаков.Физика плазмы

73. А.В.Бурдаков.Физика плазмы иУТС.

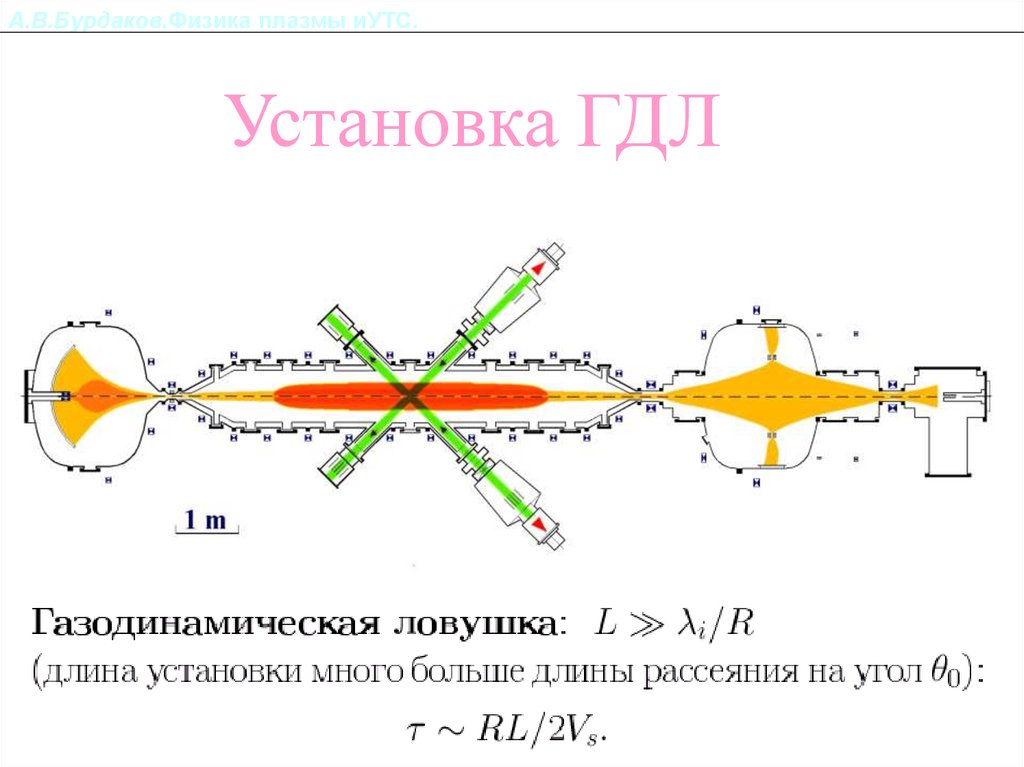
Установка ГДЛ

74.

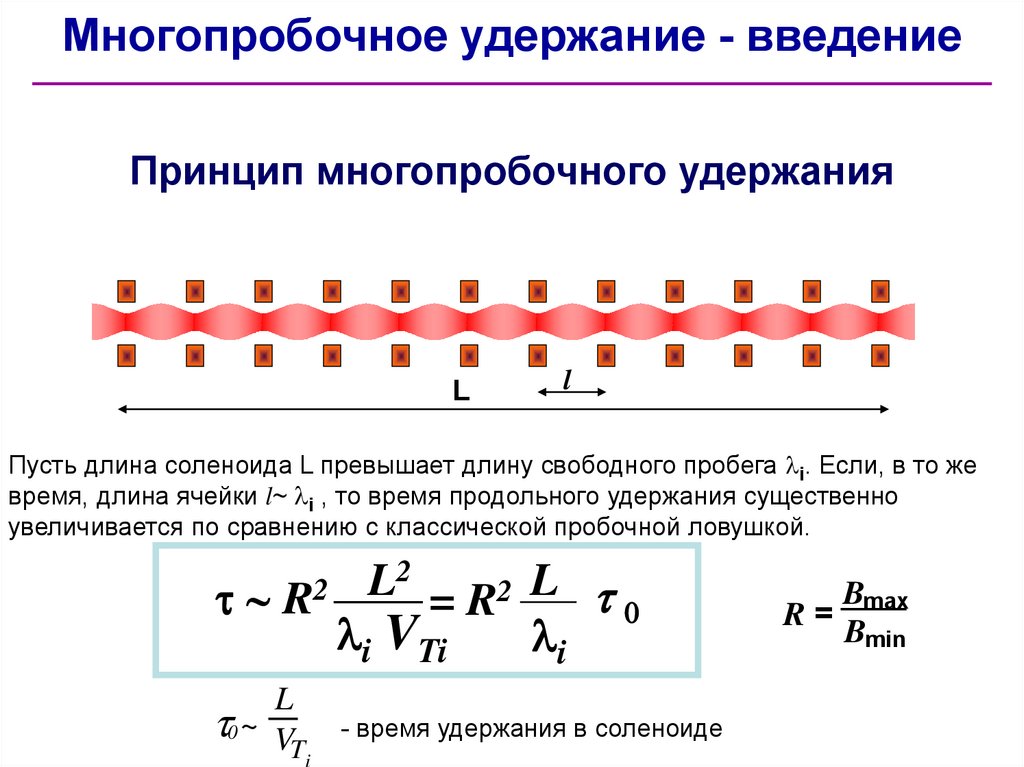
Многопробочное удержание - введение
Принцип многопробочного удержания
L
l
Пусть длина соленоида L превышает длину свободного пробега i. Если, в то же
время, длина ячейки l~ i , то время продольного удержания существенно
увеличивается по сравнению с классической пробочной ловушкой.
~
R2
L
0 ~ VT
i
L2 = R2 L
0
i VTi
i
- время удержания в соленоиде
R=
Bmax
Bmin

75.

Заключение
•Достигнута ионная температура 2кэВ:
Обнаружен эффект быстрого нагрева ионов
•Время жизни плазмы (0,5-1мс) соответствует расчетному для
многопробочной ловушки в оптимальных условиях.
•Получена величина n ~ (1.5 3) 10 12 см-3·с при ионной
температуре ~1 кэВ.
•При плотности плазмы (1-3)1015см-3 найдены условия для
макроскопической стабилизации плазмы :
-стабилизация системы пучок-плазма происходит за счет формирования винтовой
структуры магнитного поля с широм
-впервые измерена радиальная зависимость вращательного преобразования
-начаты исследования влияния винтовой конфигурации магнитного поля на
удержание плазмы

76.

А.В.Бурдаков.Физика плазмы.
Электрический разряд в газах
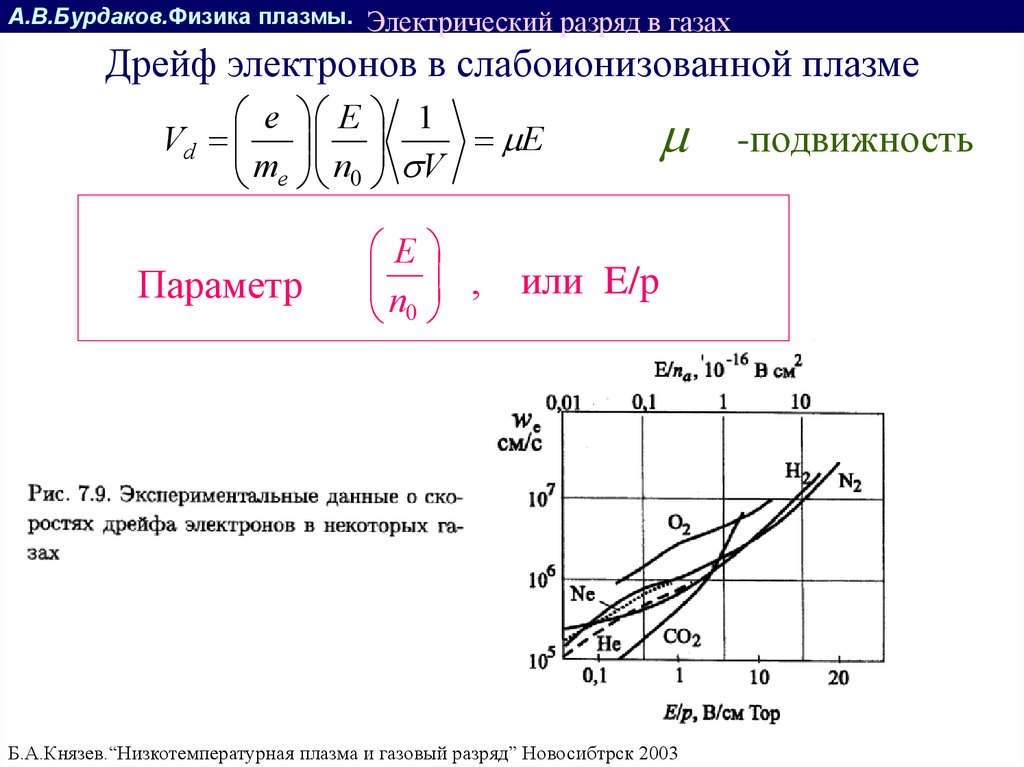
Дрейф электронов в слабоионизованной плазме
Для низкотемпературной плазмы основную роль играют
столкновения с нейтральными частицами:
ei 0
ne 2
0 E
j enV
m
e
Тогда:
Скорость дрейфа электронов в слабоионизованной плазме:
Vd ~
eE
0
me
0 ~
1
n0 V
eE
1
Vd ~
me n0 V
e E 1
Vd
E
me n0 V

77.

А.В.Бурдаков.Физика плазмы.
Электрический разряд в газах
Дрейф электронов в слабоионизованной плазме
e E 1
Vd
E
me n0 V
Параметр
E
,
n0
или E/p
Б.А.Князев.“Низкотемпературная плазма и газовый разряд” Новосибтрск 2003
-подвижность

78.

А.В.Бурдаков.Физика плазмы.
Электрический разряд в газах
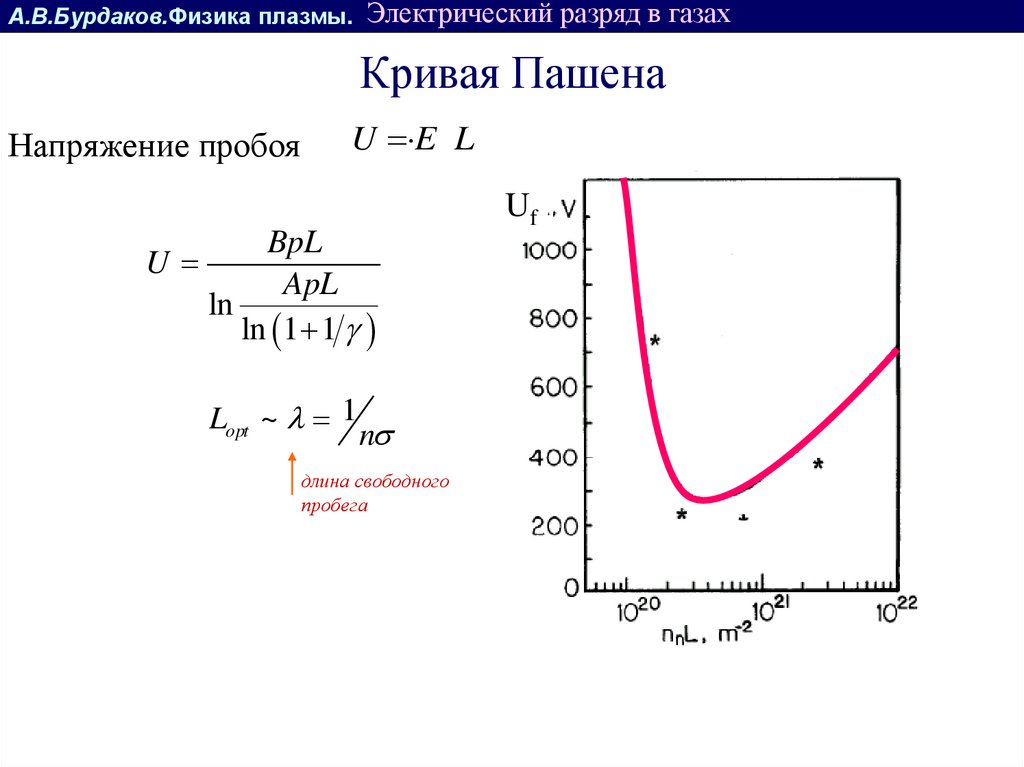
Кривая Пашена
Напряжение пробоя
U E L
Uf
BpL
U
ApL
ln
ln 1 1
Lopt ~ 1
n
длина свободного
пробега

79. А.В.Бурдаков.Физика плазмы. Н.В. Ступишин. Плазма в космосе

Плазма в космосе

80. А.В.Бурдаков.Физика плазмы. Н.В. Ступишин. Плазма в космосе

Гравитационная неустойчивость
Приводит к возникновению видимой структуры мира
Рассматривается однородная среда с учетом поля тяжести и давления вещества.
Было: В МГД-модели плазма рассматривается как сплошная среда.
u P g
Уравнение движения
r
, t mn -плотность
-давление,
u r, t -скорость среды, p r , t
g –аналог вектора E в электродинамике
Электромагнитн
е поле
E = e/r2
f=e/r
Гравитационное
поле
g=Gm/r2
f=-Gm/r
E = -grad
g = -grad G

81.

0 u P 0 g
div g 4 G
Пусть f = div u
cs2 = dP/d = P0 / 0
– скорость звука
Получим решение системы в виде:
0 div u 0
t
2 f
2
c
s f 4 G 0 f
2
t
P/P0= /
Волновое уравнение
0
Раскладываем возмущение на плоские волны: f = F(t)exp(-ikr)
Для малых k kкр возмущения
F +(k2cs2- 02)F = 0,
экспоненциально нарастают неустойчивость
где 02 = 4 G 0
Для больших k > kкр получаем
колебательные решения устойчивость
F exp( t),
где 02 k 2cs2
На больших расстояниях преобладает F
тяг
Характерный размер возмущения, для kкр
Дж сs G
0
-Джинсовская
длина волны
На малых – давление препятствует сжатию
Показываю различные структуры:
Крупномасштабная струк. Всел,
Скопл. гал, галактика, шаровые скопл,
звезды

82. А.В.Бурдаков.Физика плазмы. Н.В. Ступишин. Плазма в космосе

Звезда – система, находящаяся в равновесии
1. Гидродинамическое равновесие
r
G
G
P g 0 для всех r
g 2 m(r ) 2 4 (r )r 2 dr
r
r
0
При P=P( ), имеем систему
1 dP
Gm(r )
dr
r2
dm
4 r 2
dr
Для P ~ , = 4/3
при r 0, P(r) = P(0) -kr2
при r , P(r) ~ (R-r)4
k=const
При определенной
зависимости P=P( )
не всегда удается решить
задачу для данной М.
P
r
R
r
m(r)
Давление
газа
Для тяжелых звезд
с М ~ 100 М⊙
давление излучения
становится сравнимым
с газовым давлением
Сила гравитации
2. Тепловое равновесие
Энергия, выделяемая в звезде = Энергии, излучаемой с поверхности

83. А.В.Бурдаков.Физика плазмы. Н.В. Ступишин. Плазма в космосе

Устойчивое равновесие звезд
В равновесии полная энергия звезды отрицательна W0=Wгр+Wт < 0.
(свойство любых гравитационно связанных систем)
Wгр= -2Wт
- теорема вириала
W0 = -Wт= Wгр/2
Предположим, что мы сообщили звезде энергию (нагрели)
(Wгр+Wт )>0, тогда
(-2Wт+Wт )>0
Wт <0 – звезда остыла!
Звезды имеют отрицательную
теплоемкость!
При с>0 система была бы неустойчивой
Таким образом, излучая, звезды
постепенно разогреваются Wт >0.
Wт
W
Wт<0
t
W>0
W0
W0>0
Wгр>0
Wгр
Разогревшись звезда
расширится и остынет.

84. А.В.Бурдаков.Физика плазмы. Н.В. Ступишин. Плазма в космосе

Белые карлики – вырожденные звезды
Условие вырождения: Б ≳ n-1/3
М ~ М⊙
Т ≲ ħ2n2/3 /2m
R ~ 10 -3 – 10 -2 R⊙
Невырожденная звезда
M ~ mp n
P~ nT
R3
GM2/R2 ~ P R2
< > ~ 0.1–10 тонн/см3
T ~ GM/R ~ 1/R
n ~1/R3, а n2/3~ 1/R2
L ~ 10 -3 L⊙
Видно, что в процессе сжатия звезды Т растет медленнее, чем n2/3 ,
поэтому для электронов начинает выполняться условие вырождения.
Оценим давление вырожденного
электронного газа, p= n1/3ħ –импульс
каждого электрона P~ потоку импульса
~n1/3ħ (n1/3ħ /m) n ~ n (n1/3ħ)2 /m
P ~ n5/3ħ2 /m
Давление вырожденного
электронного газа не зависит от Т.

85. А.В.Бурдаков.Физика плазмы. Н.В. Ступишин. Плазма в космосе

Подставляя давление вырожденного электронного
газа в уравнение гидродинамического равновесия
GM2/R2 ~ P R2, получим, что
Rбк ~ М-1/3
Б.к. светятся в основном за счет расхода тепловой энергии.
Роль термоядерных реакций в недрах несущественна.
Из-за малой площади поверхности характерное время остывания Б.к.
составляет ~ 10 - 100 млрд. лет (время жизни Вселенной ~ 15млрд.лет)
Мбк < 1.44 М⊙
- предел Чандрасекара
При больших массах звезды электронный газ становится релятивистским
pe ~ n1/3ħ ~ mec
Для вырожденного релятивистского электронного газа.
Давление газа уже не может обеспечить равновесие Б.к.
При массах больших 1.44 М⊙ образуются нейтронные звезды
P ~ n4/3