Изгиб с кручением круглых стержней

1.

ИЗГИБ С КРУЧЕНИЕМ КРУГЛЫХ СТЕРЖНЕЙ
В конструкциях различных механизмов очень часто встречаются детали,
работающие на совместное действие изгиба и кручения. Характерным
примером таких деталей являются валы самых разнообразных устройств.
Силы, которые передаются на вал механизма, в общем случае приводят к
появлению в поперечных сечениях вала крутящего момента T = Mx,
изгибающих моментов My и Mz, а также поперечных сил Fy = Fz. Величиной
касательных напряжений от изгиба обычно пренебрегают, поскольку она
незначительна по сравнению с величиной касательных напряжений от
кручения. Потому рассматривают фактически сочетание кручения с чистым
изгибом.

2.

Рассмотрим вал круглого поперечного сечения (рис.6). Используя принцип
независимости действия сил, строим эпюры изгибающих моментов от
нагрузок, действующих в вертикальной и горизонтальной плоскостях, а также
эпюру крутящих моментов. Составляя полученные эпюры, отметим, что
опасными являются сечения I – I и II – II.
В каждом сечении круглого вала
имеет место прямой изгиб от действия
результирующего изгибающего момента
M M 2y M 2z .
Нормальные напряжения от этого
момента достигают наибольших значений в крайних волокнах вала и определяются по формуле
max
M
W
M 2y M 2z
W
.
(15)

3.

В любой точке контура поперечного сечения вала действуют также
максимальные касательные напряжения от кручения, связанные с величиной
крутящего момента соотношением
T
T
max
.
(16)
Wp 2 W
В формулах (15) и (16) W – осевой момент сопротивления сечения вала.
При изгибе с кручением элемент в опасной точке находится в плоском
напряженном состоянии (рис.7).
Прочность вала в опасном сечении проверяют
по формулам приемлемых теорий прочности.
Воспользуемся условием прочности, исходя из
третьей теории: 2 4 2 .
(17)
экв
Подставив в это условие выражения (15) и (16)
для напряжений σ и τ, получим:
M2 T2
экв
.
(18)
W
Если исходить из четвертой теории прочности,
то 2 3 2 .
экв

4.

Осуществив подстановки, аналогичные предыдущим, имеем:
M и2 0,75T 2
экв
.
W
Условия прочности (18) и (19) можно заменить одной формулой:
M экв
,
W
где Mэкв – эквивалентный (приведенный) момент.
экв
(19)
(20)
Для третьей теории прочности: M экв M 2 T 2 ;
Для четвертой теории прочности: M экв M 2 0,75T 2 .
Заметим, что все приведенные формулы применимы и для расчета валов
кольцевого сечения.
.

5. Задача № 4

Для
стержня
круглого
сечения,
испытывающего
совместное действие изгиба и кручения, требуется:
составить расчетную схему;
построить эпюру изгибающих моментов в вертикальной
плоскости;
построить эпюру изгибающих моментов в горизонтальной
плоскости;
построить эпюру крутящих моментов;
определить положение опасного сечения;
из расчета на прочность определить диаметр стержня в опасном
сечении.
Исходные данные:
F1 = 16 кН;
l =0,7 м;
c = 40 см;
F2 = ?;
F3 = 25 кН;
a = 40 см;
b = 25 см;
Т = 290 МПа;
nТ = 1,4

6. Решение:

1.Определяем силу F2 из расчета ΣТ = 0:
– F2 * a + F3 * b – F1 * c = 0
откуда
F3 * b F1 * c 25 * 0,25 16 * 0,40
F2
0,375
a
0,40
Значит сила F2, создающая крутящий момент,
повернута в обратном направлении.

7.

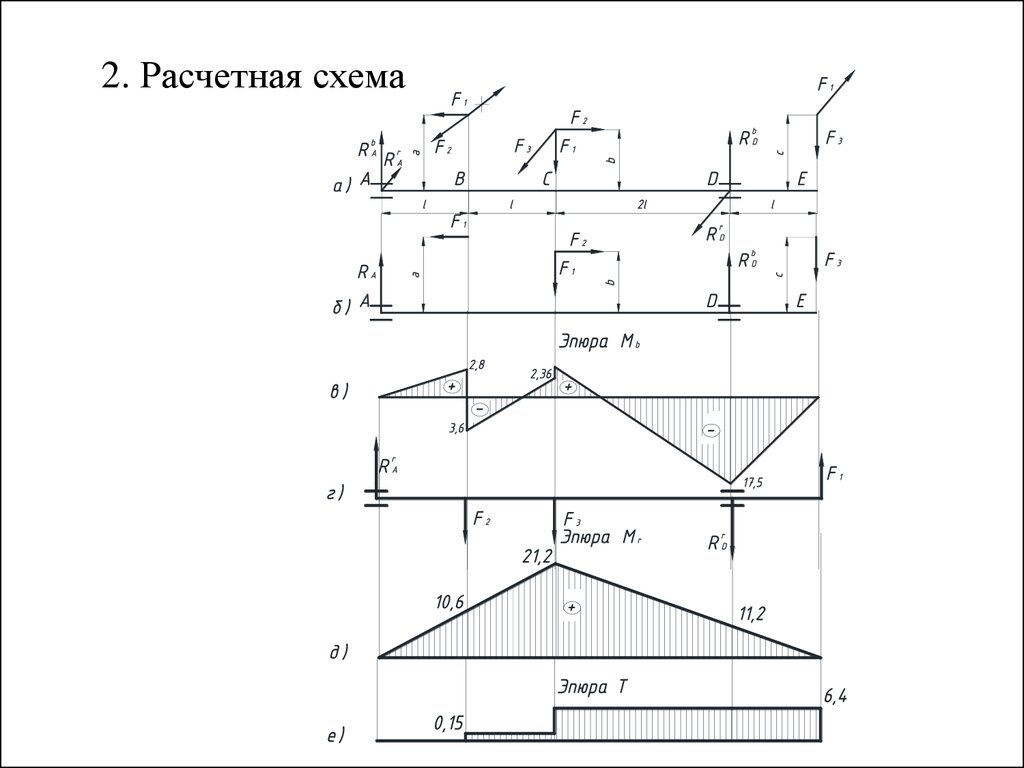
2. Расчетная схема

8.

3. Определяем вертикальные реакции в опорах A и D
и строим эпюру изгибающих моментов Mb в
вертикальной плоскости по схеме б (рис, в).
ΣMA = F1 * a – F1 * 2l – F2 * b + RDb * 4l – F3 * 5l = 0
откуда
F1 2l a F2 * b F3 * 5l
b
RD
4l
16(2 * 0,7 0,4) 0,375 * 0,25 25 * 5 * 0,7
36,98кН
4 * 0,7
ΣMD = – RAb * 4l +F1 * a + F1 * 2l – F2 * b – F3 * l = 0
откуда
F a 2l F * b F * l
RAb
1
2
4l
3
16(0,4 2 * 0,7) 0,375 * 0,25 25 * 0,7
4,02кН
4 * 0,7

9.

Проверка: Σ Fb = 0
RAb – F1 + RDb – F3 = 4,02 – 16 + 36,98 – 25 = 0
4. Определяем горизонтальные реакции в опорах A и
D и строим эпюру изгибающих моментов MГ в
горизонтальной плоскости по схеме г. Эпюра MГ
условно совмещена с плоскостью чертежа (рис. д).
ΣMA = – F2 * l – F3 * 2l – RDг * 4l + F1 * 5l = 0
откуда
F1 * 5 F2 F3 * 2
г
RD
5
16 * 5 0,375 25 * 2
5,92кН
5

10.

ΣMD = – RAг * 4l +F2 * 3l + F3 * 2l + F1 * l = 0
откуда
F2 * 3 F3 * 2 F1
г
RA
4
0,375 * 3 25 * 2 16
15,2кН
4
Проверка: Σ Fг = 0
RAг – F2 – F3 – RDг + F1 = 15,2 – 0,375 – 25 – 5,97 + 16 = 0
5. Определяем суммарные изгибающие моменты в
сечениях B, C и D, как наиболее нагруженные:
M B
6,4 2 10,6 2 12,4кНм ;
M С
2,36 2 21,2 2 21,3кНм ;
M D 17,52 11,2 2 20,8кНм ;

11.

6. Строим эпюру крутящих моментов (рис. е)
7. Наиболее опасными сечениями являются сечения C
и D, где действуют примером одинаковые изгибающие
моменты МΣС = 21,3 кНм, МΣD = 20,8 кНм, и один и тот
же крутящий момент Т = 6,4 кНм.
8. Для подбора сечения применяем четвертую гипотезу
прочности для сечения C, как наиболее опасного:
Wx
где
M 2 0,75 * Т 2
Т
nT
21,32 0,75 * 6,4 2
*106 106,32 *103 мм 3
207
290
207 МПа
1,4

12.

откуда
d 3 Wx / 0,1 3 106,32 *103 / 0,1 47,4 мм
Принимаем d = 50 мм.