Похожие презентации:
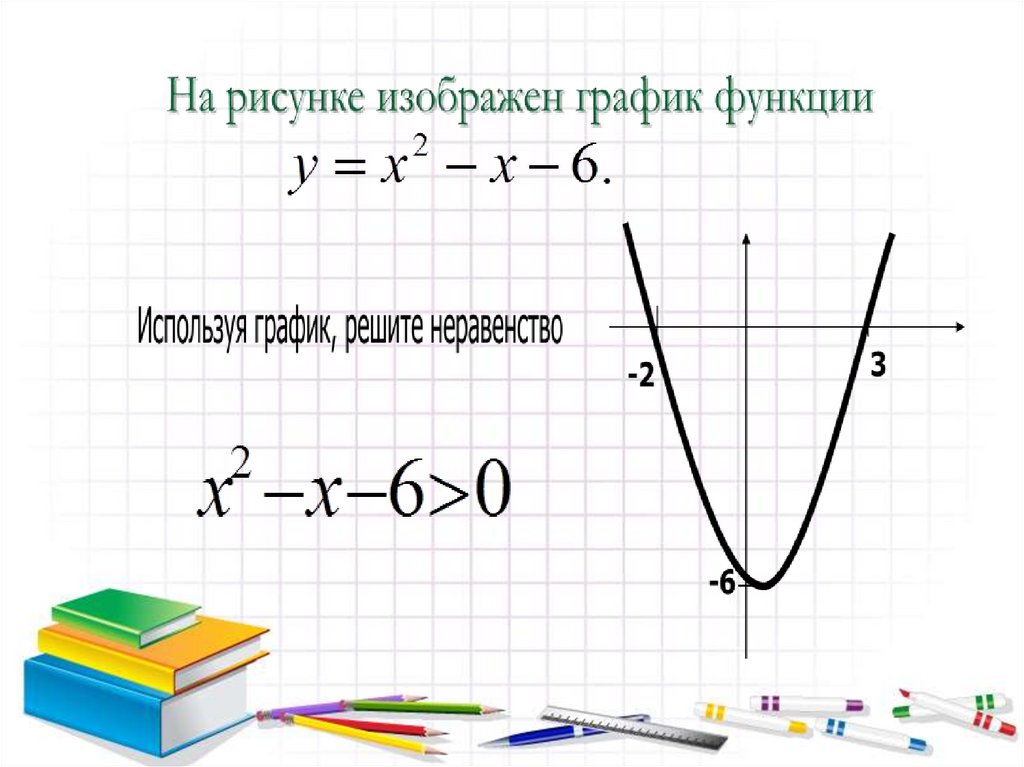
Решение неравенств второй степени с одной переменной
1.
ФИЗИКАДОМАШНЕЕ ЗАДАНИЕ:
1. КОНСПЕКТЫ $ 43 – 46 (СДАТЬ В ПОНЕДЕЛЬНИК)
2.
РЕШЕНИЕ НЕРАВЕНСТВВТОРОЙ СТЕПЕНИ
С ОДНОЙ ПЕРЕМЕННОЙ
3.
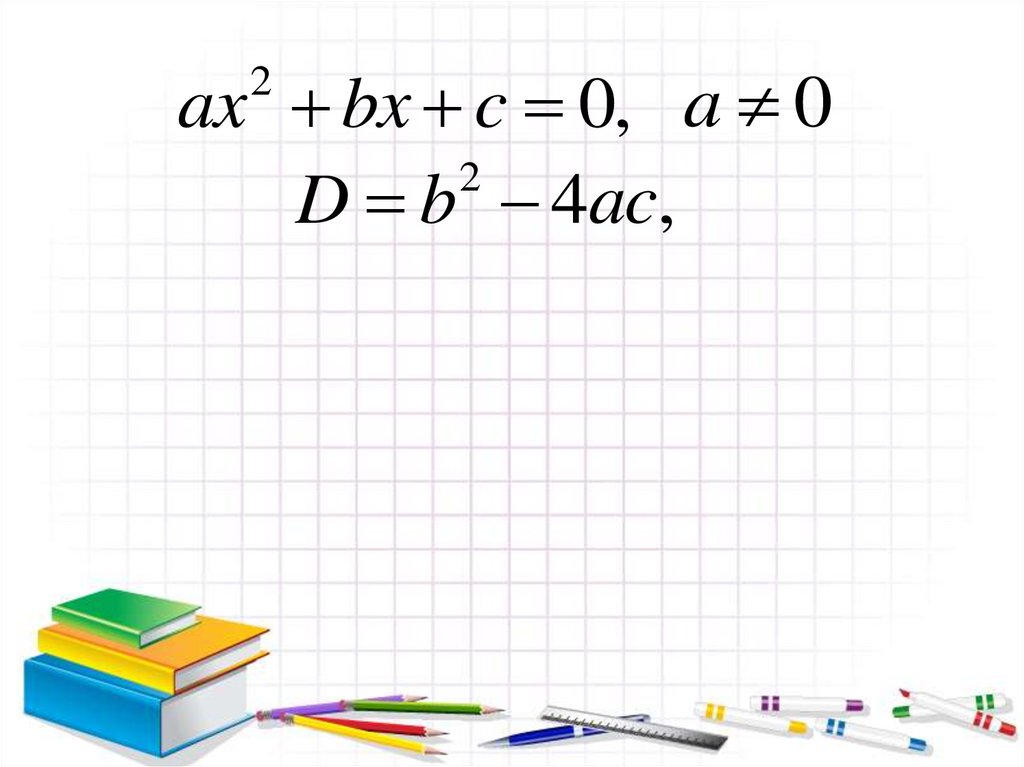
ax bx c 0, a 02
D b 4ac,
2
4.
5.
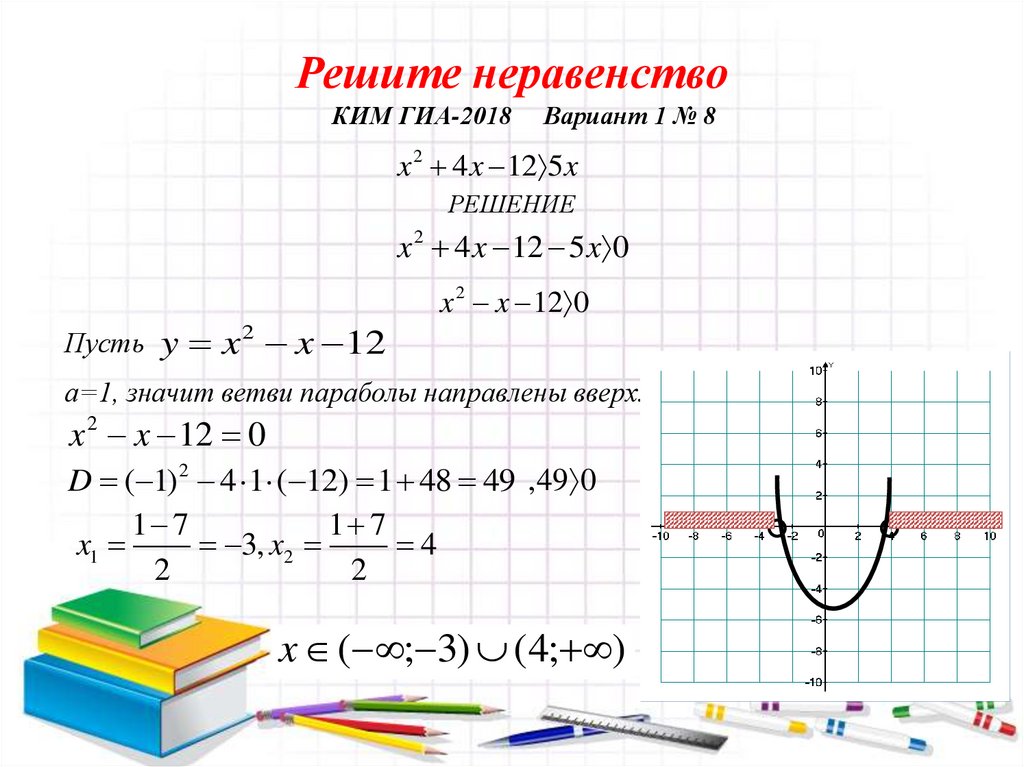
Решите неравенствоКИМ ГИА-2018
Вариант 1 № 8
x 2 4 x 12 5x
РЕШЕНИЕ
x 2 4 x 12 5 x 0
x 2 x 12 0
Пусть
y x 2 x 12
а=1, значит ветви параболы направлены вверх.
x 2 x 12 0
D ( 1) 2 4 1 ( 12) 1 48 49 ,49 0
1 7
1 7
x1
3, x2
4
2
2
x ( ; 3) (4; )
6.
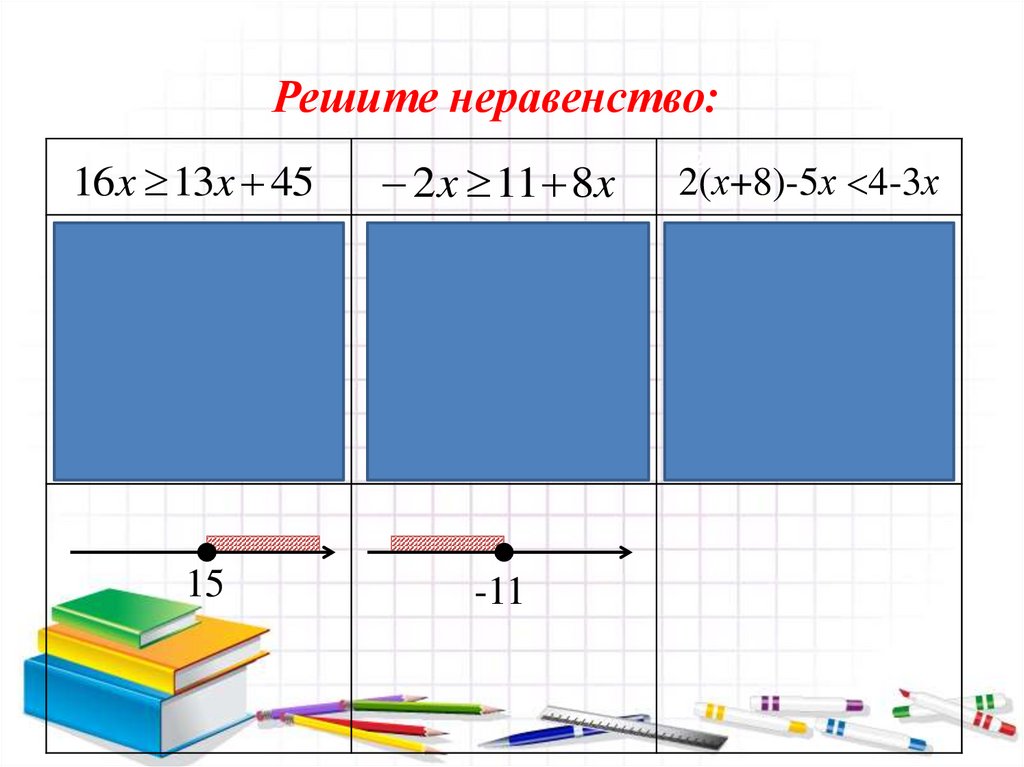
Решите неравенство:222
16x 13x 45
2x 11 8x
16x 13x 45
3x 45
x 15
2x 8x 11 2х+16-5х 4-3х,
10x 11 2х-5х+3х 4-16,
0х -12.
x 1,1
x 15;
15
x ; 11
-11
2(х+8)-5х 4-3х
Решений нет
7.
Решение неравенствметодом интервалов
8.
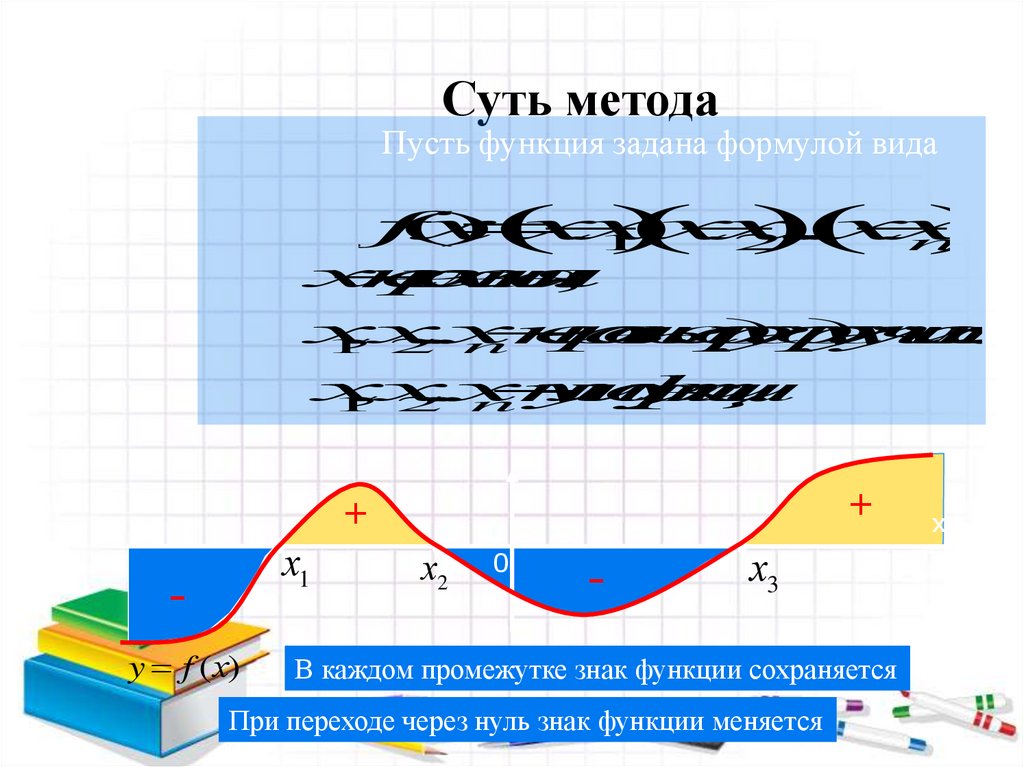
Суть методаПусть функция задана формулой вида
f
(
x
)
x
xx
x
.
.
.x
x
1
2
n
х
п
е
р
е
м
е
н
н
а
я
,
х
,ххн
.
.
.n
е
р
а
в
н
ы
е
д
р
у
г
д
р
у
г
у
ч
и
с
л
а
.
1
2
х
,хх
.
.
.n
н
у
л
и
ф
у
н
к
ц
и
и
.
1
2
у
+
+
х1
y f (х)
х2
0
-
х3
В каждом промежутке знак функции сохраняется
При переходе через нуль знак функции меняется
х
9.
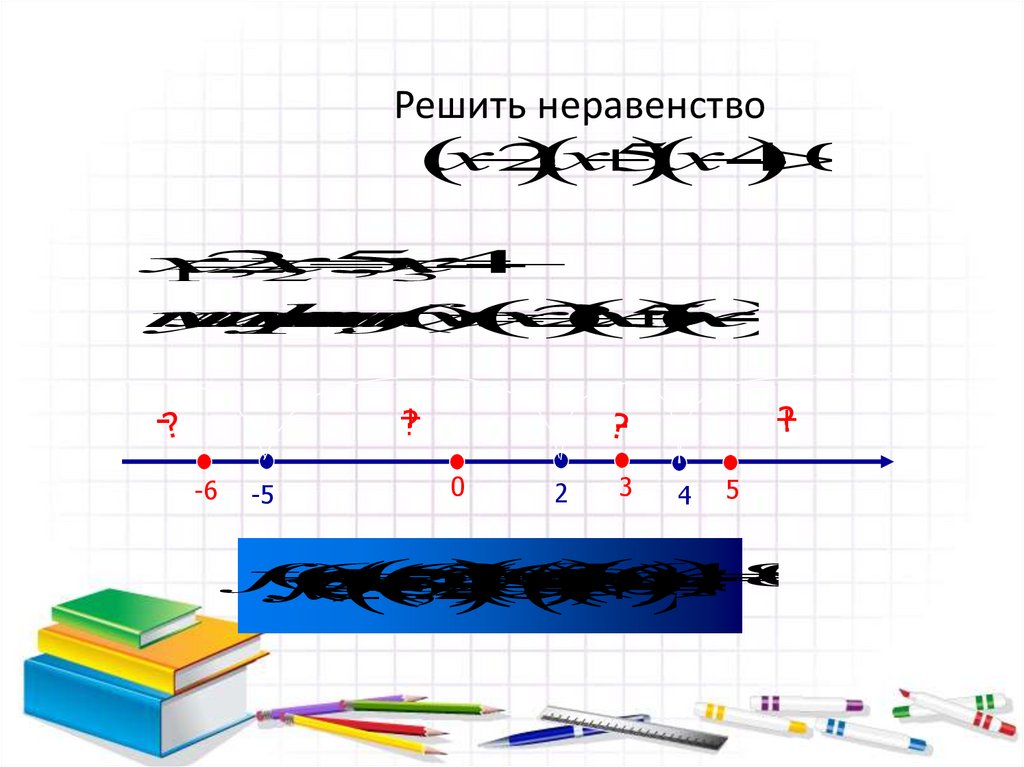
Решить неравенство2
5
4
0
х
х
х
х
2
,
х
5
,х
1
2
34
н
у
л
и
ф
у
н
к
ц
и
и
f
(
x
)
х
254
х
х
.
-
+
?
-6
0
-5
+
2
3
4
5
f
(
6
)
6
2
6
5
6
48
0
f
(
5
)
0
2
0
5
0
4
4
0
3
3
5
3
4
8
f
(
5
)
5
2
5
5
3
0
х
5
;
2
4
;
10.
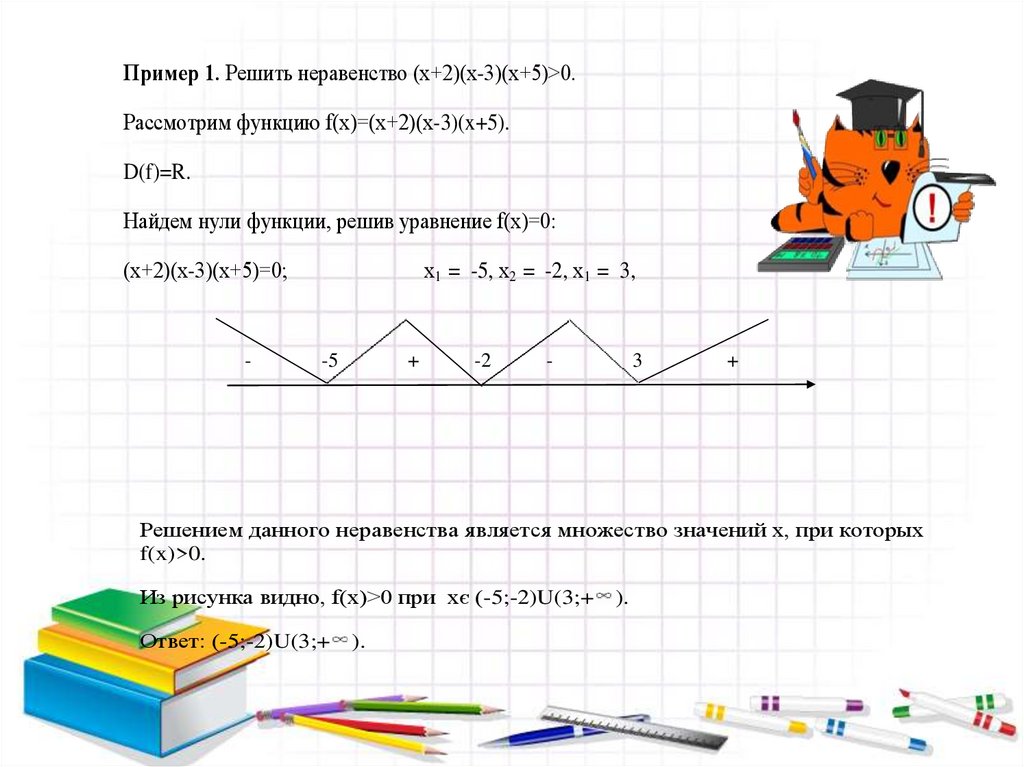
Пример 1. Решить неравенство (х+2)(х-3)(х+5)>0.Рассмотрим функцию f(x)=(x+2)(x-3)(x+5).
D(f)=R.
Найдем нули функции, решив уравнение f(x)=0:
(х+2)(х-3)(х+5)=0;
-
х1 = -5, х2 = -2, х1 = 3,
-5
+
-2
-
3
+
Решением данного неравенства является множество значений х, при которых
f(x)>0.
Из рисунка видно, f(x)>0 при хє (-5;-2)U(3;+
Ответ: (-5;-2)U(3;+
).
).
11.
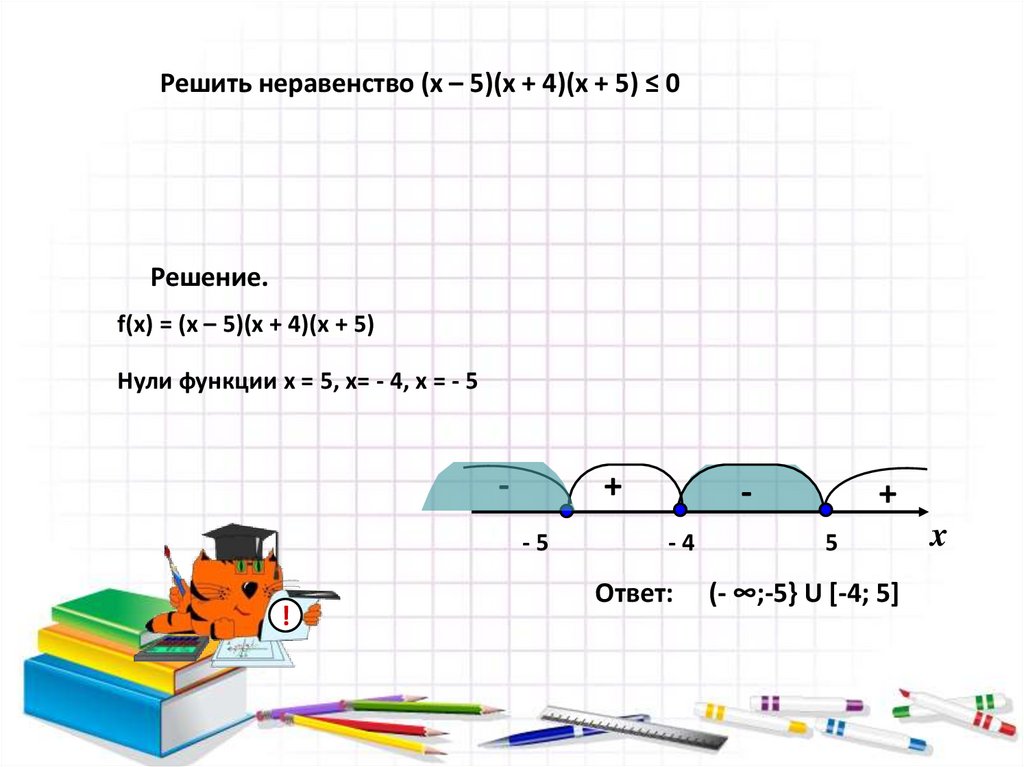
Решить неравенство (x – 5)(x + 4)(x + 5) ≤ 0Решение.
f(x) = (x – 5)(x + 4)(x + 5)
Нули функции x = 5, x= - 4, x = - 5
-
+
-5
!
-4
Ответ:
+
5
(- ∞;-5} U [-4; 5]
x
12.
ДомаРешите неравенство:
1) (х – 6) ( х + 3) ( х -18) ≤ 0
2) (Х – 2 ) ( 2х + 8) ≤ 0
3) Выбрать в учебнике еще 3 неравенства по теме и решить




 Математика
Математика








