Похожие презентации:
Производные от неявных функций. Лекция 18
1. Здравствуйте!
Лекция №182.
Производные от неявных функцийЕсли явно функция одной переменной х задается выражением
y f ( x ) , то ее неявное задание имеет вид уравнения F ( x , y ) 0 ,
не разрешенного относительно у.
Аналогично, если у зависит от ( x1 , x 2 , ..., x n ) , то неявное
задание этой функции имеет вид уравнения
F ( x1 , x 2 , ..., x n , y ) 0 ,
не разрешенного относительно у.
В общем случае можно сразу задавать m функций y1 , y 2 , ..., y m
в виде системы из m уравнений вида
F1 ( x1 , x 2 , ..., x n , y1 , y 2 , ..., y m ) 0 ,
F ( x , x , ..., x , y , y , ..., y ) 0 ,
2 1 2
n
1
2
m
.
........
Fm ( x1 , x 2 , ..., x n , y1 , y 2 , ..., y m ) 0.
3.
Начнем со случая функции одной переменной, задаваемойуравнением F ( x , y ) 0 . Представим себе, что мы каким-то
образом решили это уравнение и нашли явную зависимость у от х:
у = у(х). Если мы эту зависимость подставим в исходное
уравнение, то получим тождество
F ( x , y ( x )) 0 .
Продифференцируем это соотношение по х. Заметим, что в
левую часть аргумент х входит в двух видах: сам по себе и как
аргумент у у(х). Так как справа при любых х стоит 0, то получим
dy
Fx ( x , y ( x )) F y ( x , y ( x )) 0 ,
dx
откуда
Fx ( x , y )
dy
.
dx
F y ( x , y )
4.
Аналогично, в случае уравнения F ( x1 , x 2 , ..., x n , y ) 0 , если бынам удалось найти явный вид зависимости y y ( x1 , x 2 , ..., x n ) и
подставить его в исходное уравнение, то мы получили бы
тождество
F ( x1 , x 2 , ..., x n , y ( x1 , x 2 , ..., x n )) 0 .
Дифференцируя по хi, получим
y
Fx ( x1 , x 2 , ..., x n , y ) F y ( x1 , x 2 , ..., x n , y )
0,
x i
откуда
Fx ( x1 , x 2 , ..., x n , y )
y
.
x i
F y ( x1 , x 2 , ..., x n , y )
i
i
5.
В случае системы уравнений, определяющих y1 , y 2 , ..., y m , еслибы удалось выразить их явно, то есть найти y i y i ( x1 , x 2 , ... x n ) , то,
после подстановки их обратно в систему, мы получили бы систему
тождеств
F1 ( x1 , x 2 , ..., x n , y1 ( x1 ,... x n ), y 2 ( x1 ,... x n ), ..., y m ( x1 ,... x n )) 0 ,
F ( x , x , ..., x , y ( x ,... x ), y ( x ,... x ), ..., y ( x ,... x )) 0 ,
2 1 2
n
1
1
n
2
1
n
m
1
n
........
Fm ( x1 , x 2 , ..., x n , y1 ( x1 ,... x n ), y 2 ( x1 ,... x n ), ..., y m ( x1 ,... x n )) 0.
6.
Дифференцируя каждое из тождеств, скажем, по хi, с учетом того,что хi входит как само по себе, так и через y1 , y 2 , ..., y m , получим
F1 ( x, y ) ym
F1 ( x, y ) F1 ( x, y ) y1 F1 ( x, y ) y2
...
0,
xi
y1 xi
y2 xi
ym xi
.......... .
.
Fm ( x, y ) Fm ( x, y ) y1 Fm ( x, y ) y2 ... Fm ( x, y ) ym 0.
xi
y1
xi
y2
xi
ym
xi
Эту систему можно рассматривать как систему линейных
y m
y 1 y 2
уравнений относительно
,
, …,
. Решив ее обычными
x i
x i x i
методами, можно найти сразу все частные производные.
7.
Производные высших порядковПредставим себе, что нам задана, скажем, функция
u f ( x , y , z ) от трех переменных x, y, z. Мы можем вычислить
частные производные от этой функции по аргументам x, y, z:
f f f
,
,
.
x y z
Но эти производные сами являются функциями от тех же
переменных x, y, z. И от них снова можно вычислять производные
по тем же аргументам, которые уже будут называться
производными второго порядка
f 2 f
f 2 f
2 f yy ( x , y , z ) ; …
2 f xx ( x , y , z ) ;
y y y
x x x
Кроме этих производных есть еще и так называемые
смешанные производные. Это – производные вида
f 2 f
f 2 f
f xy ( x , y , z ) ;
f yx ( x , y , z ) .
x y x y
y x y x
От этих вторых производных можно снова вычислять производные,
которые будут называться производными третьего порядка и т.д.
8.
Теорема. Пусть у функции f ( x , y ) существуют смешанные2 f
2 f
производные
и
и они непрерывны в точке ( x 0 , y 0 ) .
x y y x
2 f 2 f
Тогда в этой точке они равны друг другу, то есть
.
y x x y
Доказательство.
2 f
2 f
Прежде всего заметим, что из существования
и
x y
y x
f
f
следует, что
и
существуют и непрерывны.
x y
Рассмотрим величину
f ( x0 h, y 0 k ) f ( x0 h, y 0 ) f ( x0 , y 0 k ) f ( x0 , y 0 )
.
W
hk
Мы проделаем с ней два преобразования.
9.
Преобразование 1. Введем функциюf ( x, y0 k ) f ( x, y0 )
,
( x )
k
у которой существует непрерывная производная
f x ( x , y 0 k ) f x ( x , y 0 )
.
( x )
k
Тогда, глядя на выражение для W, можно записать
( x0 h ) ( x0 )
.
W
h
По формуле Лагранжа
f x ( x 0 1 h , y 0 k ) f x ( x 0 1 h , y 0 )
W ( x 0 1 h )
,
k
где 0 1 1.
10.
В силу того, что аргумент x 0 1 h одинаков в обеих производных,по отношению ко второму аргументу можно снова применить
формулу Лагранжа. Тогда
W f yx ( x 0 1 h , y 0 2 k ) ,
где 0 2 1.
11.
Преобразование 2. Введем функциюf ( x0 h, y ) f ( x0 , y )
( y)
h
у которой существует непрерывная производная
f y ( x 0 h , y ) f y ( x 0 , y )
.
( y )
h
Из выражения для W видно, что
( y0 k ) ( y0 )
,
W
k
и, по формуле Лагранжа,
f y ( x 0 h , y 0 3 k ) f y ( x 0 , y 0 3 k )
,
W ( y0 3 k )
h
где 0 3 1.
12.
Опять-таки, в силу того, что аргумент y 0 3 k одинаков в обеихпроизводных, по отношению к первому аргументу можно снова
применить формулу Лагранжа:
W f xy ( x 0 4 h , y 0 3 k ) ,
где 0 4 1.
А теперь подведем итог. Исходное выражение для обоих
преобразований одно и то же. Следовательно, и результаты
должны быть равны. Поэтому
f yx ( x 0 1 h , y 0 2 k ) f xy ( x 0 4 h , y 0 3 k ) .
А теперь сделаем в этом равенстве предельный переход h 0,
k 0. Именно в этом месте и нужно предположение о
непрерывности смешанных производных в точке ( x 0 , y 0 ) , так как в
силу этой непрерывности после предельного перехода и получится
равенство
f yx ( x 0 , y 0 ) f xy ( x 0 , y 0 ) .
Теорема доказана.
13.
В общем случае имеет место следующая теорема.Теорема. Пусть у функции f ( x1 , x 2 , ..., x n ) существуют все
смешанные производные до k-го порядка включительно, и они
непрерывны. Тогда значения всех производных до k-го порядка не
зависят от того, в каком порядке производится дифференцирование.
Теперь можно окончательно установить форму записи для
смешанных производных. Пусть у функции f ( x1 , x 2 , ..., x n )
дифференцирование по х1 производилось k1 раз, по х2 – k2 раз, …,
по хп – kп раз, так что k1 k 2 ... k n k . Тогда соответствующая
производная записывается в виде
k f ( x1 , x 2 , ..., x n )
x1k x 2k ... x nk
1
2
n
14.
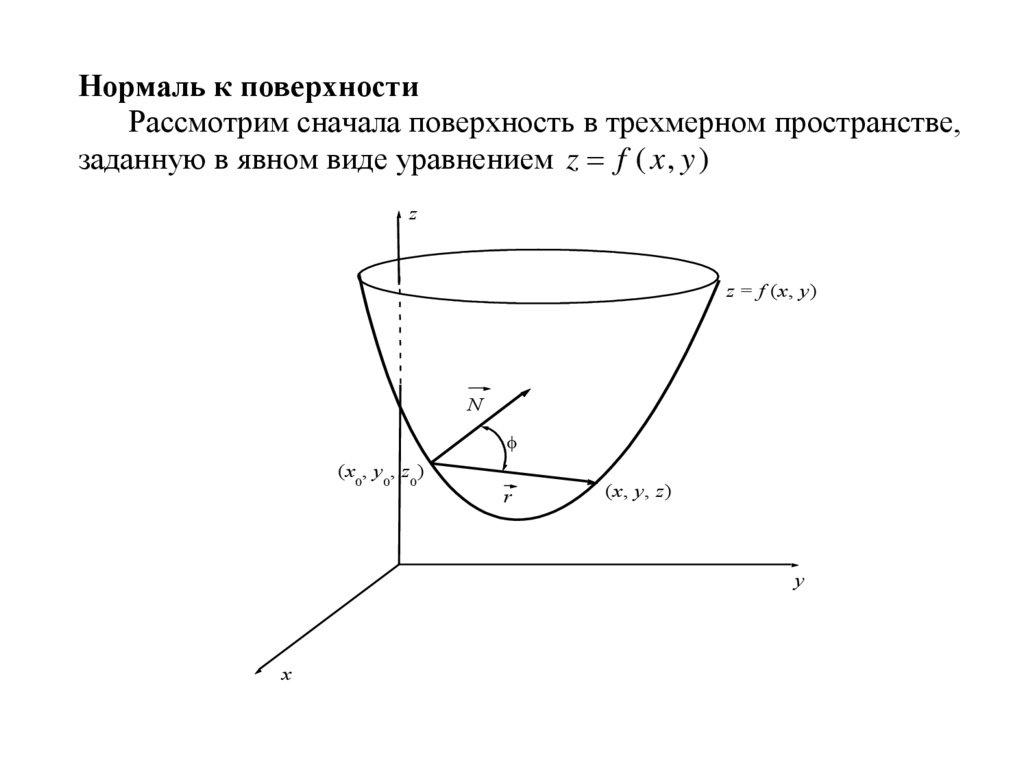
Нормаль к поверхностиРассмотрим сначала поверхность в трехмерном пространстве,
заданную в явном виде уравнением z f ( x , y )
z
z = f (x, y)
N
(x0, y0, z0)
r
(x, y, z)
y
x
15.
Пусть М0 – некоторая точка этой поверхностис координатами
( x 0 , y 0 , z 0 ) , где z 0 f ( x 0 , y 0 ) . Пусть N некоторый вектор,
проведенный из этой точки.
Сместимся из точки М0 в точку М с координатами (х, у, z),
лежащую на этой же поверхности, то есть z f ( x , y ) . Две эти
r
точки будет соединять вектор
(х – х0, у – у0, z – z0). Пусть есть
угол между векторами N и r .
Определение. Вектор N называется вектором нормали к
поверхности z f ( x , y ) в точке ( x 0 , y 0 , z 0 ) , если lim 2 ,
M M 0
когда точка М приближается к точке М0.
Другими словами это означает, что вектор N становится
перпендикулярным вектору r независимо от того, с какой стороны
точка М приближается к точке М0. Поэтому условие того, что N –
вектор нормали в точке ( x 0 , y 0 , z 0 ) можно переписать в виде
(r , N )
lim
0
M M
r
0
16.
Теорема. Если f ( x , y ) дифференцируема в точке (х0, у0), товектор нормали имеет компоненты
( f x ( x 0 , y 0 ), f y ( x 0 , y 0 ), 1) .
Доказательство.
Рассмотрим вектор N ( f x ( x 0 , y 0 ), f y ( x 0 , y 0 ), 1) . Смещаясь по
поверхности в точку (х, у), мы получим
z z 0 z f x ( x 0 , y 0 ) x f y ( x 0 , y 0 ) y o ( ) ,
2
2
(
x
)
(
y
)
x
x
x
y
y
y
r
где
, так что вектор
0 ,
0 ,
имеет компоненты
r ( x , y , f x ( x 0 , y 0 ) x f y ( x 0 , y 0 ) y o ( )) .
Тогда
получим
( r , N ) f x ( x 0 , y 0 ) x f y ( x 0 , y 0 ) y f x ( x 0 , y 0 ) x f y ( x 0 , y 0 ) y o ( )
r
( x ) 2 ( y ) 2 ( f x ( x 0 , y 0 ) x f y ( x 0 , y 0 ) y o ( )) 2
17.
Сокращая слагаемыев числителе и деля на , получим
(r , N )
o( ) /
.
2
r
y o ( )
x
1 f x ( x 0 , y 0 ) f y ( x 0 , y 0 )
Числитель этого выражения стремится к нулю при 0, а
знаменатель в любом случае больше
1. Поэтому
(r , N )
lim 0 ,
0
r
что и доказывает, что вектор N есть вектор нормали к поверхности
в точке ( ( x 0 , y 0 , f ( x 0 , y 0 )) .
18.
Пусть теперь поверхность задана неявно уравнением F ( x , y , z ) 0 .Заметим, что полученное выше выражение для нормали можно
записать в виде
z z
, , 1 .
x y
Но, по правилу нахождения производных от неявных функций,
F y ( x 0 , y 0 , z 0 )
Fx ( x 0 , y 0 , z 0 ) z
z
,
,
x
Fz ( x 0 , y 0 , z 0 ) y
Fz ( x 0 , y 0 , z 0 )
то есть
Fx ( x 0 , y 0 , z 0 ) F y ( x 0 , y 0 , z 0 )
N
,
, 1 .
Fz ( x 0 , y 0 , z 0 ) Fz ( x 0 , y 0 , z 0 )
Умножим все компоненты этого вектора на ( Fz ( x 0 , y 0 , z 0 )) . Это
изменит длину вектора N и (может быть) его направление, но не
изменит факта перпендикулярности вектору r при М М0. Поэтому
в данном случае
вектором нормали является вектор с компонентами
N ( Fx ( x 0 , y 0 , z 0 ), F y ( x 0 , y 0 , z 0 ), Fz ( x 0 , y 0 , z 0 )) .

















 Математика
Математика








