Похожие презентации:
Aproximarea numerică a funcţiilor. Metode numerice – curs 10
1.
METODE NUMERICE – curs 10Cap. 7 Aproximarea numerică a funcţiilor
7.1 Formularea problemei
fie funcţia f : [a , b] , a , b
*
- problema de calcul evalurea, în orice punct x [a , b] a următoarelor:
d
f ( x ), f ( x ), f ( x ), , f ( x ) dx , a c d b
*
*
*
c
- pot exista următoarele situaţii:
funcţia f este cunoscută analitic prin una sau mai multe expresii, în general complicate
sau dificil de evaluat, derivat sau integrat
funcţia f nu este cunoscută analitic, ci printr-un şir de valori:
{x i , f ( x i )}i 0,...,n
{x i }i 0,...,n , x i [a , b], i 0, , n
divizare a intervalului [a, b]
[a , b] : a x 0 x i x n b
2.
METODE NUMERICE – curs 10rezolvarea problemei găsirea unei funcţii cu o expresie în general simplă, uşor de
evaluat, derivat sau integrat, care să aproximeze cât mai bine pe f
x * [a , b], F( x * ) f ( x * )
construirea funcţiei aproximante, F utilizarea unei mulţimi de funcţii elementare:
M { / : [a , b] }
bază de funcţii de aproximare liniar independente
0 ( x ), 1 ( x ), , k ( x ), ,
c k k (x) 0 c k
k
F( x ) Fm ( x ) c 0 0 ( x ) c m m ( x )
polinom generalizat
0, x [a , b]
3.
METODE NUMERICE – curs 10Exemplu:
k ( x ) : 1, x , x 2 , , x m
F( x ) Pm ( x ) c 0 c1 x c m x m
aproximare cu polinoame algebrice
k ( x ) : 1, cos( x ), sin( x ), , cos(m x ), sin( m x )
F( x ) Tm ( x ) a 0 a 1 cos( x ) b1 sin( x ) a m cos(m x ) b m sin( m x )
aproximare cu polinoame trigonometrice
indiferent de abordare, rezolvarea problemei necesită răspuns la următoarele chestiuni:
determinarea setului de funcţii { k ( x )}k 0,1,...
determinarea numărului necesar de funcţii m 1
determinarea coeficienţilor polinomului generalizat {c k }k 0,1,...,m
4.
METODE NUMERICE – curs 10mulţimea de funcţii M trebuie să aibă proprietăţi suplimentare definirea unei funcţii care
să permită aprecierea “apropierii” dintre funcţia f ( x ) şi aproximanta ei, F( x ) , oricare ar fi x [a , b]
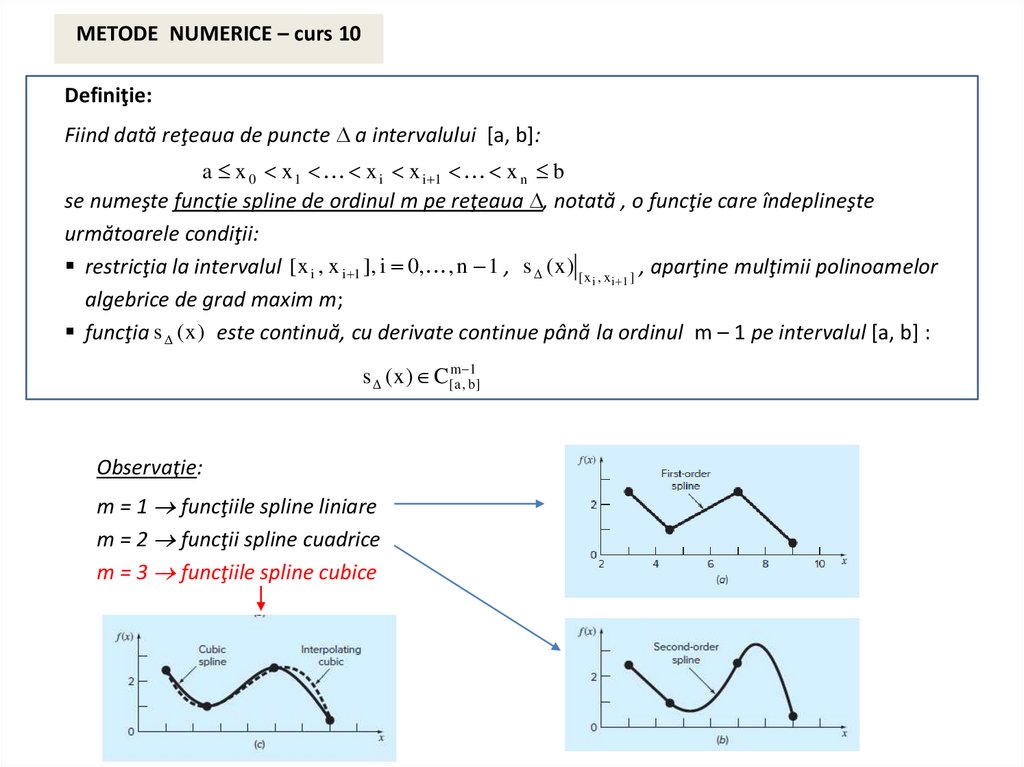
Definiţie:
Fie funcţia d : M M . Aceasta se numeşte funcţie distanţă, dacă următoarele proprietăţi sunt
îndeplinite:
oricare ar fi f , g M , atunci d (f , g ) 0 şi d (f , g ) 0 f g ;
oricare ar fi f , g M , atunci d (f , g ) d (g, f ) ;
oricare ar fi f , g, h M , atunci d (f , g ) d (f , h ) d (h , g.) .
Distanţele uzual folosite pentru cazul discret (f este cunoscută printr-un şir de valori {x i , f ( x i )}i 0,...,n ):
d (f , F) || f F || max{| f ( x i ) F( x i ) |}
0 i n
f [f ( x 0 ) f ( x n )] T
d 2 (f , F) || f F || 2
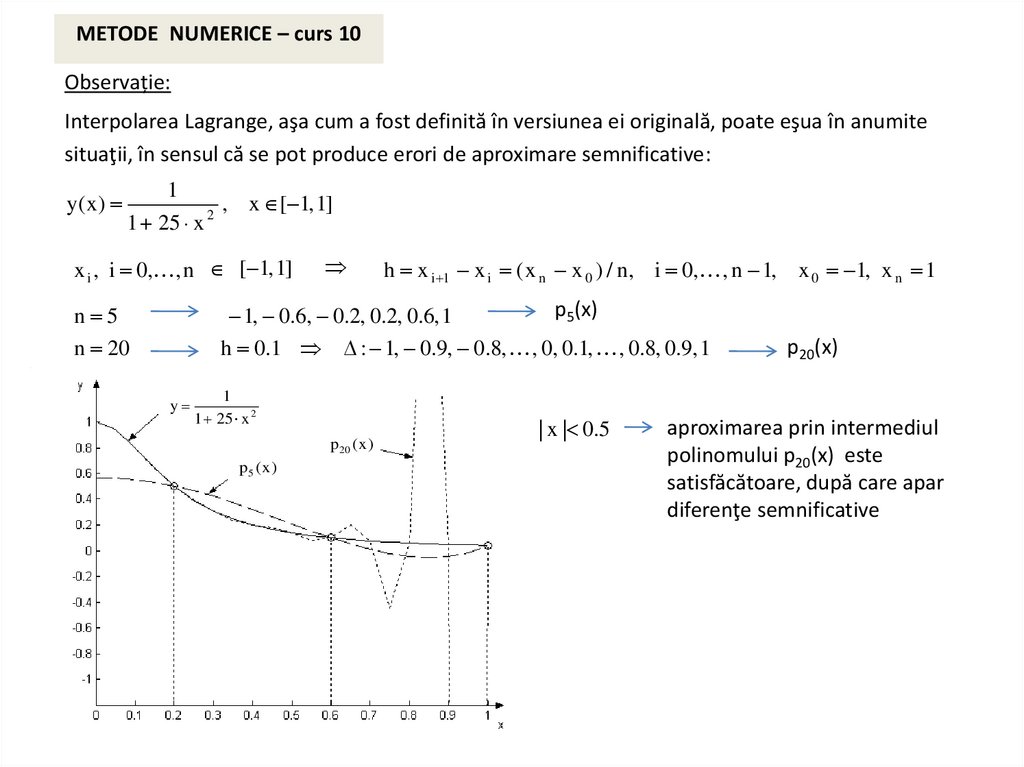
aproximarea uniformă pentru cazul discret
F [F( x 0 ) F( x n )] T
n
[f ( x i ) F( x i )] 2
i 0
aproximarea în medie pătratică pentru cazul discret
5.
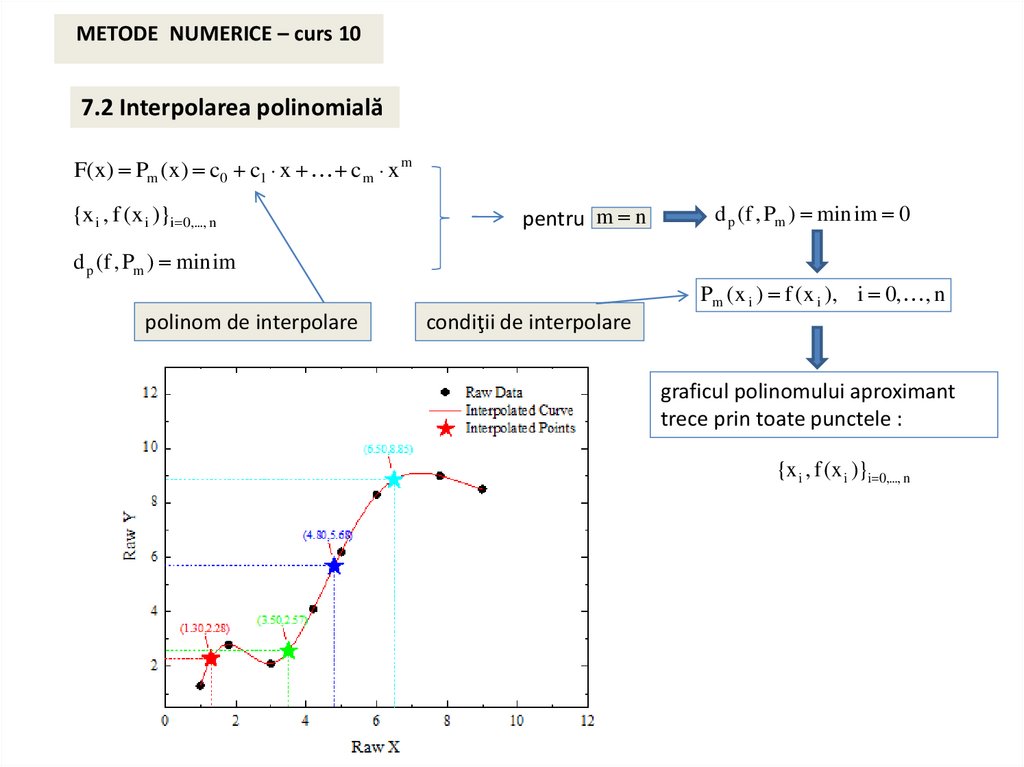
METODE NUMERICE – curs 107.2 Interpolarea polinomială
F( x) Pm ( x) c0 c1 x c m x m
{x i , f (x i )}i 0,..., n
pentru m n
d p (f , Pm ) min im 0
d p (f , Pm ) min im
Pm ( x i ) f ( x i ), i 0, , n
polinom de interpolare
condiţii de interpolare
graficul polinomului aproximant
trece prin toate punctele :
{x i , f (x i )}i 0,..., n
6.
METODE NUMERICE – curs 107.2.1 Interpolarea Lagrange
Teoremă:
În contextul problemei de interpolare, dacă punctele divizării a ,b sunt distincte, atunci oricare
ar fi y 0 , y1 , , y i , , y n , cu y i f ( x i ), i 0, , n , există şi este unic un polinom L(x) , de grad
maxim n, pentru care sunt îndeplinite condiţiile de interpolare:
L( x i ) f ( x i ), i 0, , n
Demonstraţie:
Existenţa polinomul Lagrange
L( x )
1 ( x x1 ) ( x x j ) ( x x n )
1 ( x 0 x1 ) ( x 0 x j ) ( x 0 x n )
y0
( x x 0 ) ( x x j 1 ) 1 ( x x j 1 ) ( x x n )
( x j x 0 ) ( x j x j 1 ) 1 ( x j x j 1 ) ( x j x n )
( x x 0 ) ( x x j ) ( x x n 1 ) 1
( x n x1 ) ( x n x j ) ( x n x n 1 ) 1
yn .
Lj(x)
yj
7.
METODE NUMERICE – curs 10n
L( x ) L j ( x ) y j , unde
j 0
x xk
,
x
x
k 0 j
k
n
L j (x)
j 0, , n
k j
L( x i ) f ( x i ), i 0, , n
1, i j
L j (x i )
0, i j
i, j {0, 1, , n}
baza de interpolare Lagrange determinată de către divizarea
Unicitatea reducere la absurd că mai există G(x) de grad n care interpolează f:
G ( x i ) y i , i 0, , n
Fie H( x ) L( x ) G ( x ) - grad maxim n











 Математика
Математика








