Rezolvarea sistemelor de ecuaţii algebrice neliniare (curs 9)

1.

METODE NUMERICE – curs 9
6.3 Rezolvarea sistemelor de ecuaţii algebrice neliniare
Fie f ( x ) 0 n , f : D1 D 2 , D1 , D 2 n 1 (C n 1 )
x [x 1 x n ]T
(1)
f ( x ) [f 1 ( x 1 ,..., x n ) f n ( x 1 ,..., x n )] T
f i ( x ), i 1,..., n - compunere de funcţii elementare de tip polinomial, trigonometric sau
transcendent (exponenţiale, logaritmi) în argumentele x i , i 1,..., n
Fie [ 1 n ]T , f ( ) 0 n
Metodele numerice pentru rezolvarea problemei (1) metode iterative
construiesc un şir de vectori convergent la soluţia :
- punct de start:
x
[0]
[k]
{x }k 0 , lim x
k
[ x 1[ 0] x [n0] ]T V {x D1 / || x ||p h , h 0} D1
Uzual sistemul de ecuaţii (1) se rescrie sub forma:
x
[ k 1]
g( x
[k]
x g( x )
), k 0, 1, , x
[0]
precizat
(2)
(3)
[k]

2.

METODE NUMERICE – curs 9
Teoremă:
Fie ecuaţia vectorială neliniară (1), rescrisă sub forma (2). Se consideră V o vecinătate a soluţiei .
Dacă funcţia g este o funcţie continuă pe V , iar componentele sale, g i , i 1, , n , admit derivate
parţiale în raport cu argumentele x j , j 1, , n şi satisfac la relaţia:
g i
( x ) , (0, 1), x V ,
x j
n
(4)
atunci:
[0]
[k]
i. dacă x V , atunci şi elementele şirului {x }k 0,1, definit de către relaţia (3) aparţin
vecinătăţii V ;
ii. şirul definit de către relaţia (3) converge către soluţia pentru k .
Observaţie:
Elementele din relaţia (4) se referă la componentele matricei iacobian a funcţiei g în raport cu
argumentul x :
d g ( x ) g i ( x )
G(x)
dx
x j 1 i , j n

3.

METODE NUMERICE – curs 9
6.3.1 Metode iterative explicite
metoda Newton metodă iterativă explicită
estimaţiile la un anumit pas al iterării se obţin în mod direct,
explicit, ca o funcţie de estimaţiile de la iteraţia anterioară.
- funcţia de iterare:
g( x ) x A( x ) f ( x )
A( x ) [a ij ( x )]1 i , j n
- şirul (3) converge dacă A( x )
nesingulară pentru x V
- soluţia satisface condiţia de punct fix pentru funcţia g ( x ) :
g ( ) A ( ) f ( ) 0 n
f ( ) 0 n A( ) - nesingulară
- se consideră că matricea A( x ) A constant
matricea A se alege astfel încât iacobianul funcţiei de iterare să aibă, în
modul, elementele mici sau foarte mici, pe o vecinătate a soluţiei

4.

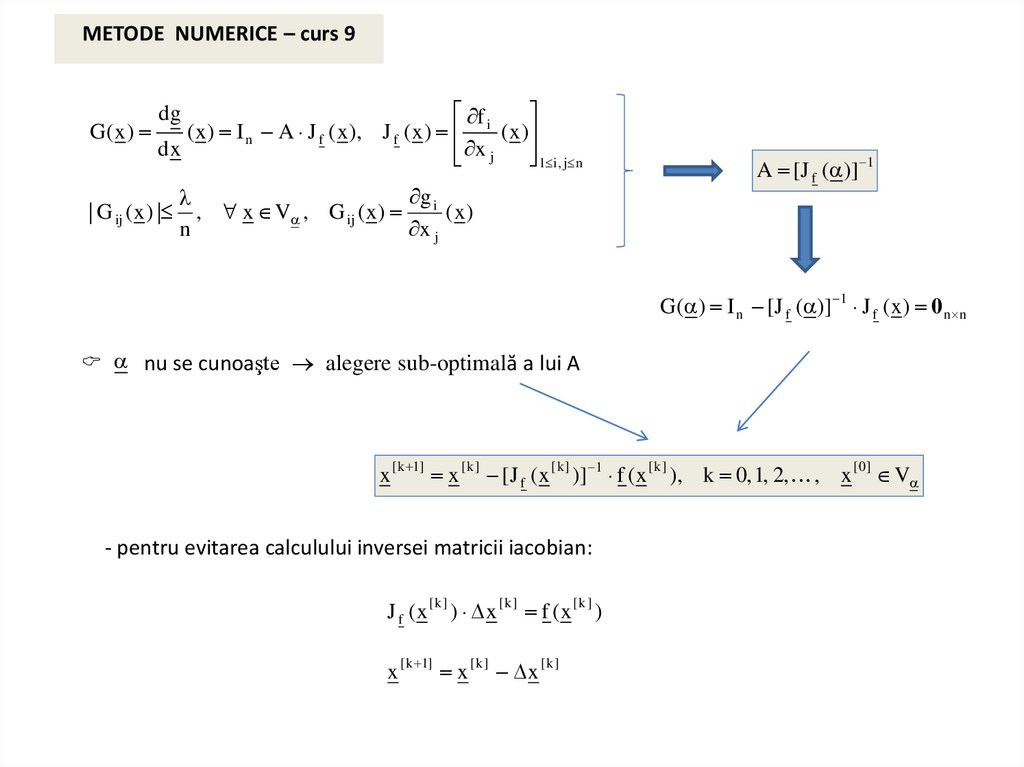
METODE NUMERICE – curs 9
G(x)
f
( x ) I n A J f ( x ), J f ( x ) i ( x )
dx
x j
1 i , j n
dg
| G ij ( x ) |
A [J f ( )] 1
g
, x V , G ij ( x ) i ( x )
n
x j
G ( ) I n [J f ( )] 1 J f ( x ) 0 n n
nu se cunoaşte alegere sub-optimală a lui A
x
[ k 1]
x
[k]
[J f ( x
[k]
)] 1 f ( x
- pentru evitarea calculului inversei matricii iacobian:
J f (x
x
[k]
[ k 1]
) x
x
[k]
[k]
f (x
x
[k]
[k]
)
[k]
), k 0, 1, 2, , x
[0]
V

5.

METODE NUMERICE – curs 9
6.3.2 Metode iterative implicite
fiecare componentă x [i k 1] nu se mai poate exprima în mod explicit în funcţie de estimaţiile
de la iteraţia anterioară
legătura dintre variabile este asigurată de către funcţiile f i
ecuaţia vectorială (1) se rescrie sub forma:
f1 (x 1 , , x n ) 0
f i (x 1 , , x n ) 0
f n ( x 1 , , x n ) 0
generalizând rezultatele de la metodele iterative pentru rezolvarea sistemelor determinate de
ecuaţii algebrice liniare şi în concordanţă cu teorema enunţată anterior
[0]
[0]
aceste metode converg către soluţia , pentru orice x V , dacă [J f ( x )] 1

6.

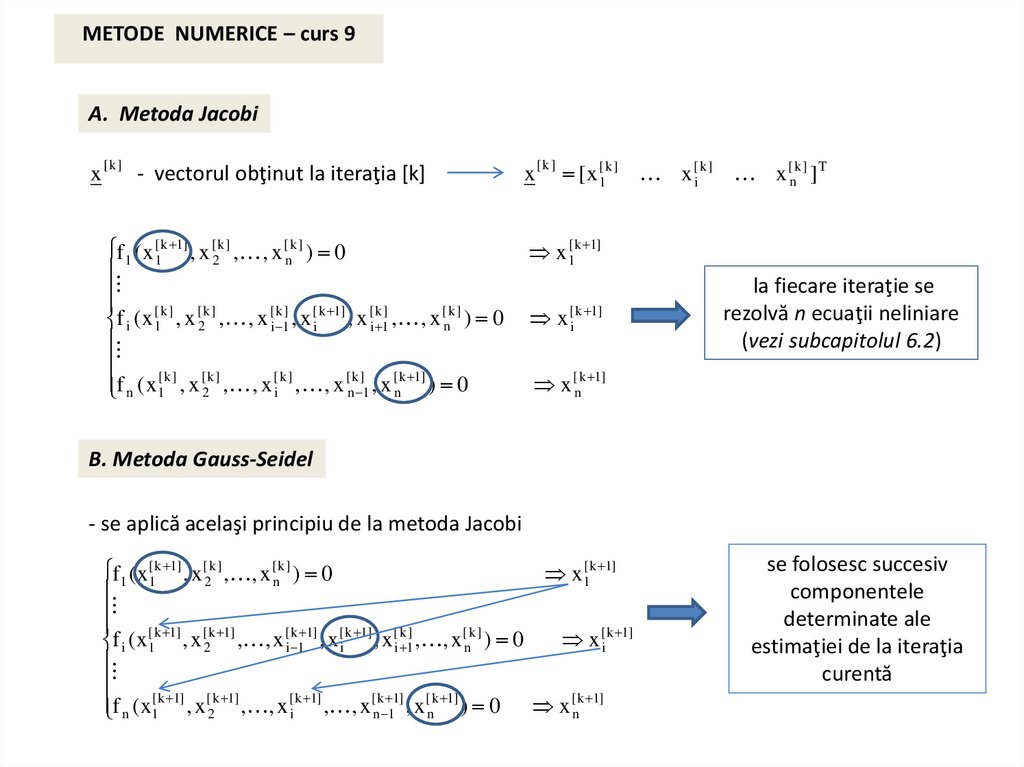
METODE NUMERICE – curs 9
A. Metoda Jacobi
x
[k]
- vectorul obţinut la iteraţia [k]
f 1 ( x 1[ k 1] , x [2k ] , , x [nk ] ) 0
[k]
[k]
[k]
[ k 1]
[k]
[k]
f i ( x 1 , x 2 , , x i 1 , x i , x i 1 , , x n ) 0
f n ( x 1[ k ] , x [2k ] , , x [i k ] , , x [nk ]1 , x [nk 1] ) 0
x
[k]
[ x 1[ k ] x [i k ] x [nk ] ] T
x 1[ k 1]
x [i k 1]
la fiecare iteraţie se
rezolvă n ecuaţii neliniare
(vezi subcapitolul 6.2)
x [nk 1]
B. Metoda Gauss-Seidel
- se aplică acelaşi principiu de la metoda Jacobi
f1 ( x1[ k 1] , x [2k ] , , x [nk ] ) 0
x1[ k 1]
[ k 1]
[ k 1]
[ k 1]
[ k 1]
[k]
[k]
x [i k 1]
f i ( x1 , x 2 , , x i 1 , x i , x i 1 , , x n ) 0
f n ( x1[ k 1] , x [2k 1] , , x [i k 1] , , x [nk 11] , x [nk 1] ) 0 x [nk 1]
se folosesc succesiv
componentele
determinate ale
estimaţiei de la iteraţia
curentă

7.

METODE NUMERICE – curs 9
6.4 Rezolvarea ecuaţiilor polinomiale
ecuaţii neliniare des întâlnite în practică ecuaţiile polinomiale
Pn ( x ) 0, Pn ( x ) a 0 x n a 1 x n 1 a n 1 x a n
a i , i 0, , n , a 0 0
Dezavantajul aplicării metodelor generale pentru rezolvarea ecuaţiilor polinomiale:
necesitatea localizării intervalelor unde ecuaţia are soluţii s-au dezvoltat procedee de separare
a rădăcinilor unui polinom ineficiente computaţional
în scopul determinării soluţiilor complexe metodele generale trebuie reformulate pentru
mulţimea numerelor complexe
A. Metode de determinare succesivă a zerourilor unui polinom
Principiul: de a pune în evidenţă divizori de grad întâi sau doi ai polinomului
divizorii sunt separaţi succesiv, în urma unui proces iterativ
- metoda Bairstow separarea divizorilor de grad doi

8.

METODE NUMERICE – curs 9
- divizorul de gradul doi: T2 ( x ) x 2 p x q, p, q
Pn ( x ) T2 ( x ) Q n 2 ( x ) R x S
Q n 2 ( x ) b 0 x n 2 b1 x n 3 b n 3 x b n 2
- în general, coeficienţii R şi S sunt funcţii neliniare în argumentele p şi q:
R R ( p, q )
S S(p, q )
- pentru ca T2 ( x ) - divizor
R ( p, q ) 0
S(p, q ) 0
(5)
aplicarea metodei implică parcurgerea unui algoritm care trebuie să combine:
- rezolvarea sistemului de ecuaţii neliniare de ordinul doi din relaţ(5)
- determinarea coeficienţilor polinomului cât, Q n 2 ( x )

9.

METODE NUMERICE – curs 9
Algoritmul Bairstow
Pn ( x ) ( x 2 p x q ) (b 0 x n 2 b n 3 x b n 2 ) R x S
- notaţii:
R
p (p, q )
p
R ( p, q )
z ; f
; J f S
q
S
(
p
,
q
)
( p, q )
p
- Rezolvarea sistemului (5) metoda Newton:
R [i 1] [i 1]
p (p , q )
S (p[i 1] , q[i 1] )
p
(6)
R
( p, q )
q
S
( p, q )
q
[J f (z
[ i 1]
)] z
[ i 1]
f (z
R [i 1] [i 1]
(p , q )
p[i 1] R (p[i 1] , q[i 1] )
q
S [i 1] [i 1] q[i 1] S(p[i 1] , q[i 1] )
(p , q )
q
p [i ] p [i 1] p [i 1]
q [i ] q [i 1] q [i 1]
- uzual p[ 0] 0, q[ 0] 0
[ i 1]
)
(7)

10.

METODE NUMERICE – curs 9
calculele implicate de rezolvarea sistemului determinat de ecuaţii neliniare (7):
[i ] det[J f (z
R (p [i 1] , q [i 1] )
P [i ]
S(p [i 1] , q [i 1] )
[ i 1]
)]
R [i 1] [i 1] S [i 1] [i 1]
(p , q ) (p , q )
p
q
R [i 1] [i 1] S [i 1] [i 1]
(p , q ) (p , q )
q
p
R [i 1] [i 1]
(p , q )
q
;
S [i 1] [i 1]
(p , q )
q
p
[ i 1]
Q[i ]
(7a)
R [i 1] [i 1]
(p , q ) R (p [i 1] , q [i 1] )
p
; (7b)
S [i 1] [i 1]
(p , q ) S(p [i 1] , q [i 1] )
p
P [i ]
Q [i ]
[ i 1]
[i ] ; q
[i ] , [i ] 0
(7c)
- condiţia de stop pentru metoda Newton, considerând precizia impusă :
| p [i 1] q [i 1] | | (P [i ] Q [i ] ) / [i ] |
(8)

11.

METODE NUMERICE – curs 9
Calculul derivatelor funcţiilor R şi S
- din (6) rezultă relaţiile de recurenţă:
b k a k p b k 1 q b k 2
k 0,1, , n 2
(9)
b 1 b 2 0
b n 1 R , b n p b n 1 S
R b n 1
p p
R b ;
n 1
q
q
- notaţii:
b n
b n 1
S
(
b
p
b
)
b
p
n 1
n 1
p p n
p
p
S
b
b
(b n p b n 1 ) n p n 1
q q
q
q
notaţii
(10)
b k
p c k 1 , k 1, , n
b
k d k 2 , k 2, , n
q
- derivare în raport cu p:
c k b k p c k 1 q c k 2 , k 0, , n 1, c 2 c 1 0
(11)
- derivare în raport cu q:
d k b k p d k 1 q d k 2 , k 0, , n 2, d 2 d 1 0
(12)

12.

METODE NUMERICE – curs 9
- din relaţiile (11) şi (12) se observă că :
dk ck
(11), (12)
pentru
k 0, , n 2
b k c k p c k 1 q c k 2 , k 0, , n 2, c 2 c 1 0
(10), (11), (12)
R
R
c n 2 ,
c n 3 ,
p
q
S
c n 1 b n 1 p c n 2 ,
p
S
c n 2 p c n 3
q
(13)
Algoritm (schiţă):
* iniţializare p, q
* calcul coeficienţi ck, dk ( relaţiile (11) şi (12) )
* rezolvare sistem (7) noi valori pentru p, q (relaţiile (7a), (7b) şi (7c) )
* calcul coeficenti bk (relaţia (9))
* verificare conditie stop (relaţia (8))

13.

METODE NUMERICE – curs 9
B. Metode de determinare simultană a zerourilor unui polinom
- ecuaţia:
Pn ( x ) 0, Pn ( x ) a 0 x n a 1 x n 1 a n 1 x a n
a i , i 0, , n , a 0 0
se transformă astfel încât polinomul din membrul stâng să fie monic ( a 0 1 )
Q n ( x ) 0, Q n ( x ) x n 1 x n 1 n 1 x n ,
i a i / a 0 , i 1, , n .
- polinomului Q n ( x ) i se asociază o matrice A, astfel încât:
det( I n A) Q n ( )
valorile proprii ale lui A vor fi chiar rădăcinile polinomului Q n ( x )
- o modalitate uzuală de construire a matricei A matrice de tip Frobenius
0,
F [f ij ]1 i , j n , f ij 1,
n j 1 ,
i 1, , n 1, j 1, n , j i 1
i 1, , n 1, j i 1
i n , j 1, , n
det( I n F) x n 1 x n 1 n 1 x n
0
0
⋯
0
−