Rezolvarea numerică a sistemelor supradeterminate de ecuaţii algebrice liniare în sensul celor mai mici pătrate

1.

METODE NUMERICE – curs 5
Cap. 3 Rezolvarea numerică a sistemelor supradeterminate de
ecuaţii algebrice liniare în sensul celor mai mici pătrate
3.1 Formularea problemei
A x b, A m n , b m 1 , x n 1
m n
- sistem supradeterminat
Definiţii:
m n
A
are coloanele liniar independente (monică), dacă vectorii coloană ai săi sunt liniar
independenţi: n
j a j 0m
j 1
j 0, j 1, , n
subspaţiul imagine al matricei A: Im(A) {y m 1 / y A x , x n 1 } m 1
subspaţiul nul (nucleu) al matricei A:
N(A) {x n 1 / A x 0 m } n 1

2.

METODE NUMERICE – curs 5
Propoziţie:
Pentru orice matrice A
A este o matrice monică;
rang( A ) n ;
N (A) {0 n } ;
m n
, m n , următoarele afirmaţii sunt echivalente:
T
matricea A A este pozitiv definită, deci inversabilă (nesingulară).
Concluzie:
Problema de calcul are o soluţie unică dacă:
b Im(A)
în ipoteza că rang(A) = n.
Trebuie reformulată problema de calcul pentru a asigura existenţa unei soluţii în caz contrar.
Principiul folosit este minimizarea unei funcţii criteriu de tipul:
V ( x ) || b A x ||
x
*
- pseudosoluţie a sistemului dacă V ( x ) minim
*

3.

METODE NUMERICE – curs 5
Condiţii de minim:
T
V ( x )
V ( x )
x {V ( x )}
0 nx1
x
x
1
n
V - diferenţiabilă
not
x x {V ( x )} x {V ( x )} x { Tx {V ( x )}} 0
1
1
1 T
1 m 2
2
2
V( x ) || b A x || 2 || r || 2 r r ri
2
2
2
2 i 1
Problema de calcul devine:
2
|| b A x || 22 min
{||
b
A
x
||
2}
n 1
*
x
Condiţii de minim:
x* - pseudosoluţie în sensul celor mai mici pătrate
sistem de ecuaţii normale
x {V( x )} (1 / 2) 2 (A T A x A T b) 0 n
x {V( x )} (1 / 2) 2 (A T A) 0

4.

METODE NUMERICE – curs 5
3.2 Triangularizarea ortogonală a matricelor
3.2.1 Matrici ortogonale
Definiţie:
Fie o matrice Q m m . Matricea Q se numeşte ortogonală dacă este îndeplinită una din relaţiile:
QT Q Im
Q [q 1 q i
Q T Q 1
q j q m ], q i m 1 , i 1,..., m
q i q j 0, i j, i, j 1,..., m; || q i || 22 1
T
Proprietate o matrice ortogonală păstrază norma vectorială euclidiană:
z m 1 , || Q z || 22 || z || 22

5.

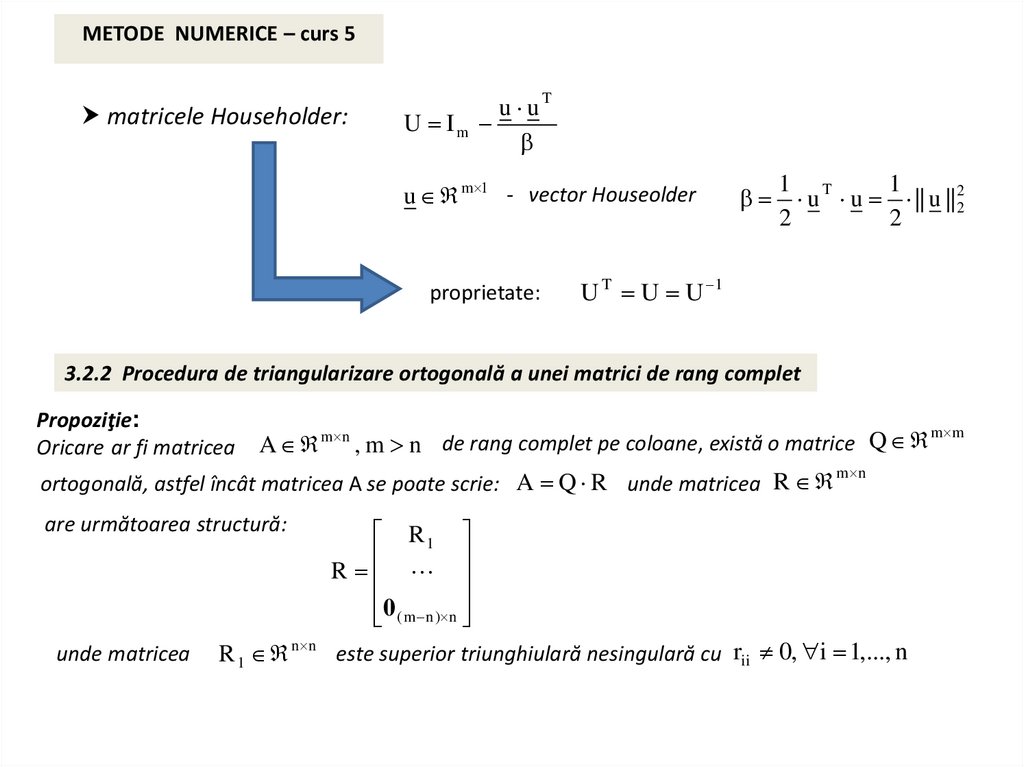
METODE NUMERICE – curs 5
matricele Householder:
u u
U Im
T
u m 1 - vector Houseolder
proprietate:
1 T
1
u u || u || 22
2
2
U T U U 1
3.2.2 Procedura de triangularizare ortogonală a unei matrici de rang complet
Propoziţie:
Oricare ar fi matricea
A m n , m n de rang complet pe coloane, există o matrice Q
m n
ortogonală, astfel încât matricea A se poate scrie: A Q R unde matricea R
are următoarea structură:
unde matricea
R1
R
0 ( m n ) n
R 1 n n este superior triunghiulară nesingulară cu rii 0, i 1,..., n
m m

6.

METODE NUMERICE – curs 5
Demonstraţia este constructivă şi constituie însuşi algoritmul de triangularizare ortogonală a
matricei A (factorizare QR a matricii A):
atribuie A 1 A
pentru k 1, n execută
* determinare matrice Householder U k astfel încât:
( U k A k ) i ,k 0, i k 1,..., m
atribuie A k 1 U k A k
atribuie R A n 1
Fie [ 1 k 1 k
k 1 m ] T m 1 coloana k a matricii Ak
m
m m
2k i2 0 ⇒ U k
astfel încât
i k
U k Im u k u k / k ,
T
k || u k || 22 / 2
k sign ( k )
m
i2 ,
i k
U k [ 1 k 1 k
u k [0 0 u k , k
0 0]T ,
u k 1,k
u m,k ]T
u k ,k k k , u i ,k i , i k 1,..., m,
k k u k , k , k k .
2k 2k

7.

METODE NUMERICE – curs 5
m
i2 0
2k
Daca
i k
k 0
u k 0m
⇒ i 0, i k,..., m ⇒
⇒ U k nu există
k 0 (| k | impus )
Fie [ 1 m ] T
T
u
u
k
k
Uk Im
k
T
uk
k
m
u j,k j
j k
k
T
u
u
k
k
k
⇒ Uk uk
⇓
U
Daca
[ j] [ 1 j
0 0] T m 1
k
i 1,..., k 1
i ,
i
i u i ,k , i k ,..., m
j 1,..., k 1
⇒
U k [ j] [ j]

8.

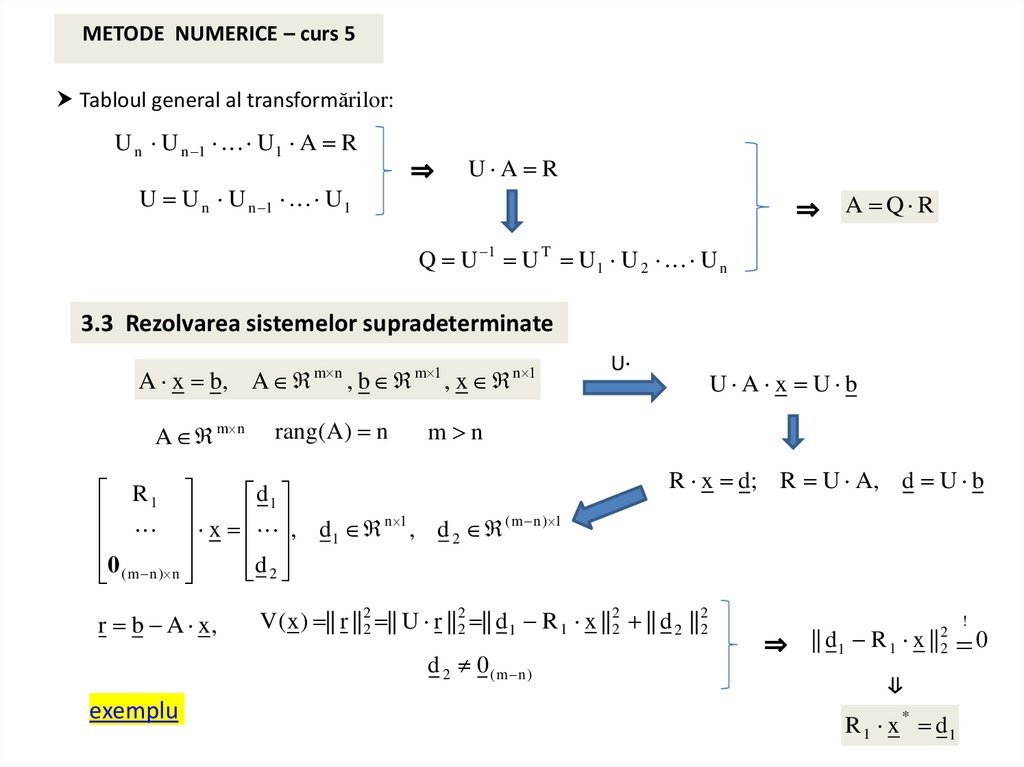
METODE NUMERICE – curs 5
Tabloul general al transformărilor:
U n U n 1 U 1 A R
U U n U n 1 U 1
⇒
U A R
⇒ A Q R
Q U 1 U T U 1 U 2 U n
3.3 Rezolvarea sistemelor supradeterminate
A x b, A m n , b m 1 , x n 1
A m n
rang(A) n
R x d; R U A , d U b
V( x ) || r || 22 || U r || 22 || d 1 R 1 x || 22 || d 2 || 22
d 2 0 (m n )
exemplu
U A x U b
m n
R1
d1
n 1
( m n ) 1
x , d 1 , d 2
0 ( m n ) n
d 2
r b A x,
U
⇒ || d 1 R 1 x
|| 22
⇓
R 1 x d1
*
!
0

9.

METODE NUMERICE – curs 5
Cap. 4 Calculul valorilor şi vectorilor proprii
4.1 Formularea problemei
n n
- Se consideră o matrice reală, pătratică, de ordin n: A
Definiţie:
n n
Oricare ar fi matricea A
, un număr în general complex, λ , se numeşte valoare
n 1
proprie a matricei A dacă există un vector, x C , x 0 n astfel încât:
A x x
x – vector propriu al matricii A asociat valorii proprii λ
( I n A ) x 0 n
x 0n
I n A - singulară
ecuaţie caracteristică
polinom caracteristic
p n ( ) det( I n A) 0
p n ( ) n 1 n 1 n 1 n
i , i 1,..., n

10.

METODE NUMERICE – curs 5
Teoremă de existenţă:
Orice matrice pătratică reală, de ordin n, are exact n valori proprii, în general complexe şi nu
neapărat distincte, care coincid cu rădăcinile polinomului caracteristic ataşat matricei. Dacă
există valori proprii complexe, atunci acestea apar în perechi complex conjugate.
Orice matrice A n n are cel puţin un vector propriu.
Nu se recomandă calculul numeric al valorilor proprii prin rezolvarea ecuaţiei caracteristice deoarece:
- rezolvarea ecuaţiilor polinomiale este o problemă prost condiţionată;
- coeficienţii polinomului caracteristic volum mare de calcule erori
Metodele practice pentru calculul numeric al valorilor proprii proceduri iterative
- matricea A adusă la formă canonică Schur prin transformări ortogonale de asemănare

11.

METODE NUMERICE – curs 5
4.2 Forma canonică Schur
Definiţie:
n n
Două matrici, A, A' n n , se numesc ortogonal asemenea, dacă există o matrice ortogonală , Q
astfel încât:
A' Q T A Q
Proprietăţi:
Matricile ortogonal asemenea au aceleaşi valori proprii:
i (A) 'i (A' ), i 1,..., n
Relaţia dintre vectorii proprii ai două matrici ortogonal asemenea:
x i (A) Q x 'i (A' ), i 1,..., n
Definiţie:
O matrice se spune că este în formă bloc superior triunghiulară, dacă are următoarea structură:
T11
0
T
0
T12
T22
T1m
T2 m
Tii , i 1,..., m - matrici pătratice
, Tii pi pi
0 Tmm
formă cvasi-superior triunghiulară
p i 1, 2 , i 1, m

12.

METODE NUMERICE – curs 5
Teoremă de existenţă:
~
Oricare ar fi matricea A n n , există o matrice ortogonală Q n n , astfel încât matricea:
~T
~
S
Q
A
Q
forma canonică Schur reală a matricei A
este în formă cvasi-superior triunghiulară. Blocurile diagonale de ordin întâi ale matricei S reprezintă
valorile proprii reale ale matricei A şi ale matricei S, iar blocurile diagonale de ordin doi au valori
proprii complex conjugate reprezentând valori proprii complex conjugate ale matricelor A şi S.
Observaţii:
~
~
coloanele matricii Q n n ,q k , k 1,..., n
vectori Schur ai matricii A
Demonstraţia teoremei este constructivă algoritmul QR
4.3 Algoritmul QR pentru calculul formei canonice Schur
Principiu: construcţia unui şir de matrici ortogonal asemenea convergent la forma canonică Schur
A 0 A, A 1 ,..., A k ,...
A k a ijk
1 i , j n
a ijk k
0
a ik 1 ,i k
0
A k k
S
i j 2
i=1,...,n-1

13.

METODE NUMERICE – curs 5
sedefineşte şirul de matrici {A k }k 0 , A 0 A
pas QR cu deplasare explicită
A k k I n Q k R k , A k 1 R k Q k k I n
Q k n n - ortogonală;
R k n n - superior triunghiulară
k - deplasare (cu rol de accelerare a convergenţei)
Propoziţie:
Matricele şirului QR sunt ortogonal asemenea: A k 1 Q Tk A k Q k
Observaţie:
- algoritmul original QR consumator de timp se foloseşte o formă optimizată
Forma implementabilă a algoritmului QR cu deplasare explicită
parcurge două faze de lucru:
faza 1 – pregătitoare (zerorizare elemente de sub sub-diagonala principală)
faza 2 – aplicare algoritm QR matricii obţinută la faza 1
se obţine forma canonică Schur

14.

METODE NUMERICE – curs 5
Faza 1
- procedură directă de aducere a matricei A la forma superior Hessenberg (H)
H=
A=
0
c1 c2 ck
cn-2
- se folosesc matrici Householder în scopul anulării, coloană cu coloană, a elementelor
matricei A situate sub sub-diagonala principală
- algoritm:
atribuie A 1 A
pentru k 1, n 2 execută
* determinare matrice Householder astfel încât:
( U k 1 A k ) i ,k 0, i k 2,..., n
atribuie A'k 1 U k 1 A k
atribuie A k 1 A'k 1 U Tk 1 A'k 1 U k 1
atribuie H A n 1

15.

METODE NUMERICE – curs 5
sinteza matricii Householder, Uk+1
U k 1 I n
T
(u k 1 u k 1
/ k 1 )
u k 1 [0 0 u k 1,k 1 u n ,k 1 ]T
k 1
sign (a [kk ]1,k )
n
(a [i,kk] ) 2 ,
i k 1
u k 1,k 1 a [kk ]1,k k 1
u i ,k a [i ,kk] , i k 2,..., n , k 1 k 1 u k 1,k 1
tabloul general al transformărilor:
U n 1 U 2 A U 2 U n 1 H
UT
U
H U A UT
sunt parcurse exact ( n – 2 ) iteraţii