Похожие презентации:
Calculul valorilor şi vectorilor proprii
1.
METODE NUMERICE – curs 6Cap. 4 Calculul valorilor şi vectorilor proprii
4.1 Formularea problemei
n n
- Se consideră o matrice reală, pătratică, de ordin n: A
Definiţie:
n n
Oricare ar fi matricea A
, un număr în general complex, λ , se numeşte valoare
n 1
proprie a matricei A dacă există un vector, x C , x 0 n astfel încât:
A x x
x – vector propriu al matricii A asociat valorii proprii λ
( I n A ) x 0 n
x 0n
I n A - singulară
ecuaţie caracteristică
polinom caracteristic
p n ( ) det( I n A) 0
p n ( ) n 1 n 1 n 1 n
i , i 1,..., n
2.
METODE NUMERICE – curs 6Teoremă de existenţă:
Orice matrice pătratică reală, de ordin n, are exact n valori proprii, în general complexe şi nu
neapărat distincte, care coincid cu rădăcinile polinomului caracteristic ataşat matricei. Dacă
există valori proprii complexe, atunci acestea apar în perechi complex conjugate.
Orice matrice A n n are cel puţin un vector propriu.
Nu se recomandă calculul numeric al valorilor proprii prin rezolvarea ecuaţiei caracteristice deoarece:
- rezolvarea ecuaţiilor polinomiale este o problemă prost condiţionată;
- coeficienţii polinomului caracteristic volum mare de calcule erori
Metodele practice pentru calculul numeric al valorilor proprii proceduri iterative
- matricea A adusă la formă canonică Schur prin transformări ortogonale de asemănare
3.
METODE NUMERICE – curs 64.2 Forma canonică Schur
Definiţie:
n n
Două matrici, A, A' n n , se numesc ortogonal asemenea, dacă există o matrice ortogonală , Q
astfel încât:
A' Q T A Q
Proprietăţi:
Matricile ortogonal asemenea au aceleaşi valori proprii:
i (A) 'i (A' ), i 1,..., n
Relaţia dintre vectorii proprii ai două matrici ortogonal asemenea:
x i (A) Q x 'i (A' ), i 1,..., n
Definiţie:
O matrice se spune că este în formă bloc superior triunghiulară, dacă are următoarea structură:
T11
0
T
0
T12
T22
T1m
T2 m
Tii , i 1,..., m - matrici pătratice
, Tii pi pi
0 Tmm
formă cvasi-superior triunghiulară
p i 1, 2 , i 1, m
4.
METODE NUMERICE – curs 6Teoremă de existenţă:
~
Oricare ar fi matricea A n n , există o matrice ortogonală Q n n , astfel încât matricea:
~T
~
S
Q
A
Q
forma canonică Schur reală a matricei A
este în formă cvasi-superior triunghiulară. Blocurile diagonale de ordin întâi ale matricei S reprezintă
valorile proprii reale ale matricei A şi ale matricei S, iar blocurile diagonale de ordin doi au valori
proprii complex conjugate reprezentând valori proprii complex conjugate ale matricelor A şi S.
Observaţii:
~
~
coloanele matricii Q n n ,q k , k 1,..., n
vectori Schur ai matricii A
Demonstraţia teoremei este constructivă algoritmul QR
4.3 Algoritmul QR pentru calculul formei canonice Schur
Principiu: construcţia unui şir de matrici ortogonal asemenea convergent la forma canonică Schur
A 0 A, A 1 ,..., A k ,...
A k a ijk
1 i , j n
a ijk k
0
a ik 1 ,i k
0
A k k
S
i j 2
i=1,...,n-1
5.
METODE NUMERICE – curs 6sedefineşte şirul de matrici {A k }k 0 , A 0 A
pas QR cu deplasare explicită
A k k I n Q k R k , A k 1 R k Q k k I n
Q k n n - ortogonală;
R k n n - superior triunghiulară
k - deplasare (cu rol de accelerare a convergenţei)
Propoziţie:
Matricele şirului QR sunt ortogonal asemenea: A k 1 Q Tk A k Q k
Observaţie:
- algoritmul original QR consumator de timp se foloseşte o formă optimizată
Forma implementabilă a algoritmului QR cu deplasare explicită
parcurge două faze de lucru:
faza 1 – pregătitoare (zerorizare elemente de sub sub-diagonala principală)
faza 2 – aplicare algoritm QR matricii obţinută la faza 1
se obţine forma canonică Schur
6.
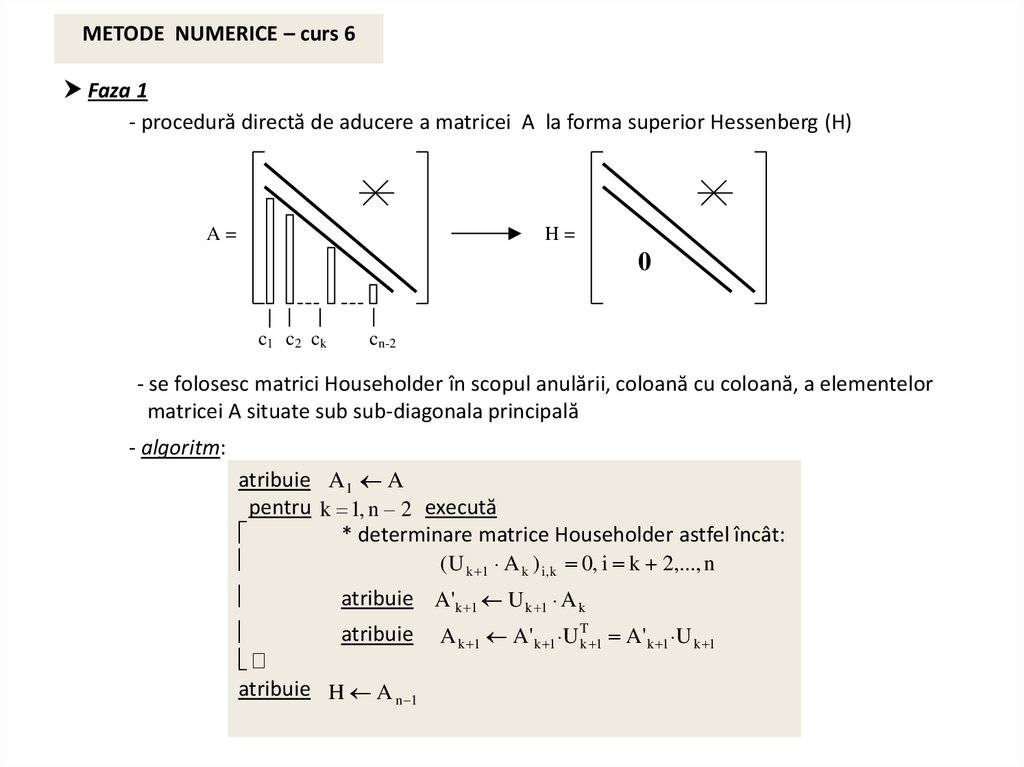
METODE NUMERICE – curs 6Faza 1
- procedură directă de aducere a matricei A la forma superior Hessenberg (H)
H=
A=
0
c1 c2 ck
cn-2
- se folosesc matrici Householder în scopul anulării, coloană cu coloană, a elementelor
matricei A situate sub sub-diagonala principală
- algoritm:
atribuie A 1 A
pentru k 1, n 2 execută
* determinare matrice Householder astfel încât:
( U k 1 A k ) i ,k 0, i k 2,..., n
atribuie A'k 1 U k 1 A k
atribuie A k 1 A'k 1 U Tk 1 A'k 1 U k 1
atribuie H A n 1
7.
METODE NUMERICE – curs 6sinteza matricii Householder, Uk+1
U k 1 I n
T
(u k 1 u k 1
/ k 1 )
,
u k 1 [0 0 u k 1,k 1 u n ,k 1 ]T
k 1
sign (a [kk ]1,k )
n
(a [i,kk] ) 2 ,
i k 1
u k 1,k 1 a [kk ]1,k k 1
u i ,k a [i ,kk] , i k 2,..., n , k 1 k 1 u k 1,k 1
tabloul general al transformărilor:
U n 1 U 2 A U 2 U n 1 H
UT
U
H U A UT
sunt parcurse exact ( n – 2 ) iteraţii
8.
METODE NUMERICE – curs 6Faza 2
- procedură iterativă de construcţie a unui şir QR pornind de la matricea H
- scopul: anularea unora din elementele de pe sub-diagonala principală a matricei H
S11
H=
S=
0
Sii
0
0
0
Smm
pas QR cu
deplasare explicită
-algoritmul QR cu deplasare explicită parcurge următoarele etape:
1. determinare deplasare , ;
2. atribuire H H I n ;
(n-1) iteraţii
3. descompunere H Q R , R - matrice superior triunghiulară, Q - matrice ortogonală;
4. atribuire H R Q ;
5. refacere deplasare H H I n ;
6. corecţie matrice H (efectuare test de decuplare);
7. atribuire S H şi efectuare teste reluare algoritm QR (de la etapa 1).
9.
METODE NUMERICE – curs 6Detaliere etape:
Etapa 1 - determinare deplasare
- viteza maximă de convergenţă pentru h n ,n
Etapa 2 - deplasarea se scade de pe diagonala principală a matricei H
- se lucrează în continuare cu această matrice
Etapa 3 – factorizare QR a matricei H obţinută la etapa 2
- se zerorizează elementele de pe sub-diagonala principală (n – 1 elemente)
- se utilizează matrici de rotaţie plană Givens (ortogonale, nesimetrice)
planul (k, k+1)
k+1
(k)r
h k ,k rk
R
0
h
k 1,k
(k+1)r
hk+1,k
(rk, 0)
ck
R
d k
k
hk,k
dk
c k
c k cos (θ)
h k ,k
d k sin (θ)
h k 1,k
rk
rk
10.
METODE NUMERICE – curs 6I k 1
Pk 0 2 ( k 1 )
0( n k 1 ) ( k 1 )
- matricea de rotaţie Givens:
0( k 1 ) 2
R
0( n k 1 ) 2
0( k 1 ) ( n k 1 )
0 2 ( n k 1 )
I n k 1
n n
- se poate demonstra:
I k 1
Pk PkT 0 2 ( k 1 )
0( n k 1 ) ( k 1 )
0( k 1 ) 2
Q
0( n k 1 ) 2
c 2k d 2k
Q
0
0( k 1 ) ( n k 1 )
0 2 ( n k 1 )
I n k 1
1 0
2
2
c k d k 0 1
0
n n
Pk PkT I n
11.
METODE NUMERICE – curs 6- tabloul transformărilor de la etapa 3:
Pn 1 P1 H R
Q T Pn 1 P1
Q P1T PnT 1
R – matrice superior triunghiulară
Etapa 4 – matricea R se înmulţeşte la dreapta cu matricea Q, rezultatul fiind stocat în H:
H R P1T PnT 1
Etapa 5 – se adună deplasarea la elementele de pe diagonala prinicipală a matricii H
Etapa 6 – test de decuplare
Pk
h k ,k
h k ,k 1
h 'k ,k
h k 1,k
h k 1,k 1
0
k 1,..., n 1
PkT
h 'k ,k 1
h 'k 1,k 1
h "k ,k
h "k ,k 1
h "k 1,k
h "k 1,k 1
| h k 1,k | | h "k 1,k |
- inegalitatea strictă elementul din poziţia (k+1, k) devine zero în forma canonică Schur
12.
METODE NUMERICE – curs 6- rol de decuplare a blocurilor diagonale din forma canonică Schur test de decuplare:
dacă | h "k 1,k | (| h "k ,k | | h "k 1,k 1 |) atunci
atribuie h "k 1,k 0
Etapa 7 – testele care condiţionează reluarea sau nu a algoritmului QR
Mi
0
sii
0
0
sii
si,i+1
si+1,i
si+1,i+1
0
concluzii privind structura formei canonice Schur:
- nu există pe sub-diagonala principală două elemente consecutive nenule
- blocuri de ordinul doi pe diagonala matricei S au valori proprii complex conjugate
13.
METODE NUMERICE – curs 6testele care se realizează la această etapă sunt:
(T1)
dacă i {1, 2, ..., n 2} pentru care s i 1,i 0 şi s i 2,i 1 0 atunci
matricea S nu este în forma canonică Schur (reluare de la etapa 1)
(T2)
dacă i care să satisfacă (T1), dar i {1, 2, ..., n 1} pentru care
s i ,i
blocul M i
s i 1,i
s i ,i 1
are valori proprii reale atunci
s i 1,i 1
matricea S nu este în forma canonică Schur (reluare de la etapa 1)
Tabloul general al transformărilor din faza a doua a algoritmului QR:
S [Pn[s ]1 P1[s ] ] [Pn[1 ]1 P1[1] ] H [(P1[1] ) T (Pn[1 ]1 ) T ] [(P1[s ] ) T (Pn[s ]1 ) T ]
PT
P
P H PT S
14.
METODE NUMERICE – curs 6În urma aplicării ambelor faze ale formei implementabile a algoritmului QR rezultă:
P U A UT PT S
~
~
QT P U
Q UT PT
~
~
S QT A Q
forma implementabilă a algoritmului QR este o procedură stabilă numeric, iar forma
canonică Schur calculată pentru o matrice A, notată prin , coincide cu forma canonică
Schur exactă, S, a matricei A uşor perturbată, Â A E :
Ŝ S A E , || E || || A ||
exemplu
15.
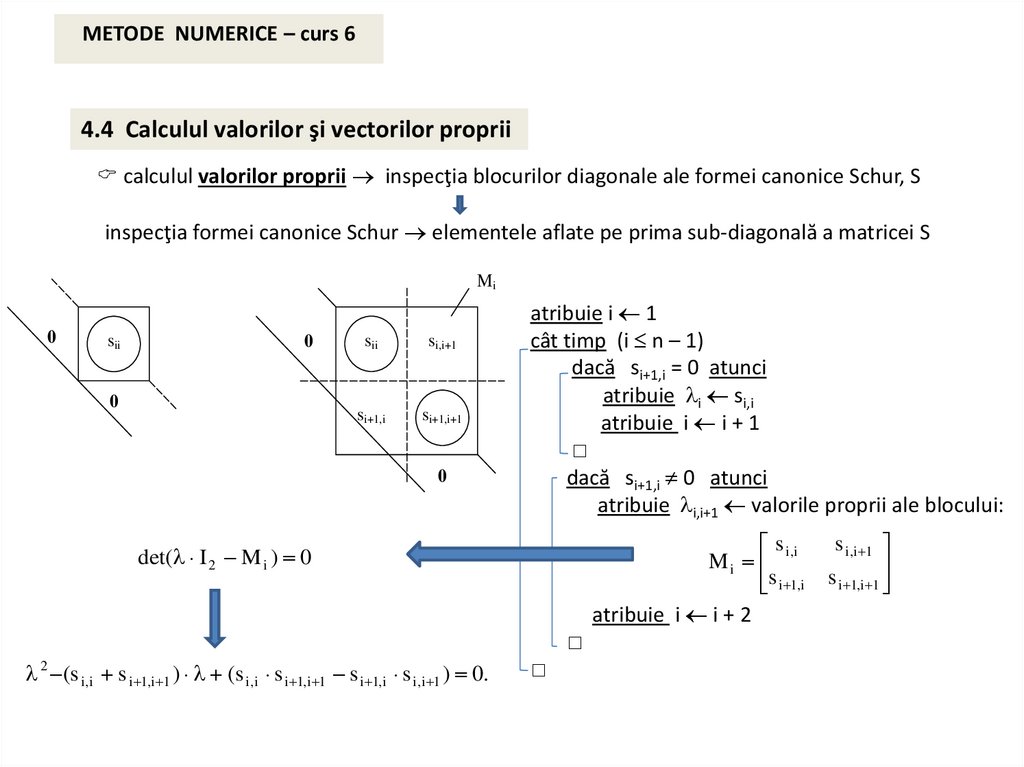
METODE NUMERICE – curs 64.4 Calculul valorilor şi vectorilor proprii
calculul valorilor proprii inspecţia blocurilor diagonale ale formei canonice Schur, S
inspecţia formei canonice Schur elementele aflate pe prima sub-diagonală a matricei S
Mi
0
sii
0
0
sii
si,i+1
si+1,i
si+1,i+1
0
atribuie i 1
cât timp (i n – 1)
dacă si+1,i = 0 atunci
atribuie i si,i
atribuie i i + 1
dacă si+1,i 0 atunci
atribuie i,i+1 valorile proprii ale blocului:
s i ,i
Mi
s i 1,i
atribuie i i + 2
det( I 2 M i ) 0
2 (s i ,i s i 1,i 1 ) (s i ,i s i 1,i 1 s i 1,i s i ,i 1 ) 0.
s i ,i 1
s i 1,i 1
16.
METODE NUMERICE – curs 6calculul vectorilor proprii
~
x i Q r i , i 1,..., n
unde
S r i i r i , i 1,..., n
~
în practică vectorii Schur ai matricei A vectorii coloană ai matricei Q
~
Q [~
q1 ~
qi
~
qn ]
~
q i , i 1,..., n
- ortogonali
|| ~
q i || 22 1, i 1,..., n
~
dacă i s ii (s i 1,i 0) atunci x i q i
~
~
~
~
dacă i , i 1 C (s i 1,i 0) atunci x i q i j q i 1 , x i 1 q i j q i 1














 Математика
Математика








