Ecuaţii şi sisteme de ecuaţii neliniar. Formularea problemei (curs 8)

1.

METODE NUMERICE – curs 8
Cap. 6 Ecuaţii şi sisteme de ecuaţii neliniare
6.1 Formularea problemei
Fie f ( x ) 0 n , f : D1 D 2 , D1 , D 2 n 1 (C n 1 )
x [x 1 x n ]T
(1)
f ( x ) [f 1 ( x 1 ,..., x n ) f n ( x 1 ,..., x n )] T
f i ( x ), i 1,..., n - compunere de funcţii elementare de tip polinomial, trigonometric sau
transcendent (exponenţiale, logaritmi) în argumentele x i , i 1,..., n
(1)
- ecuaţie (n = 1) / sistem de ecuaţii (n 2) neliniare
Fie [ 1 n ]T , f ( ) 0 n
Metodele numerice pentru rezolvarea problemei (1) metode iterative
construiesc un şir de vectori convergent la soluţia :
- punct de start:
x
[0]
[k]
{x }k 0 , lim x
[ x 1[ 0] x [n0] ]T V {x D1 / || x ||p h , h 0} D1
k
[k]

2.

METODE NUMERICE – curs 8
Definiţie:
Se numeşte formulă de iterare sau şir de iterare (de rang k şi ordin m) o relaţie de recurenţă de forma:
x
[k]
g(k, x
[ k 1]
,x
[ k 2]
, , x
[k m]
[0]
), x , , x
[ m 1]
V , 1 m k
formulă de iterare staţionară de ordinul m g nu depinde de k
uzuale sunt metodele iterative care folosesc formule staţionare de ordin m = 1 :
x
[k]
g( x
[ k 1]
)
(2)
Propoziţie:
O metodă iterativă de tipul (2) se spune că este convergentă pe domeniul V , dacă oricare ar fi
x , y V , există (0,1) astfel încât, într-o normă vectorială oarecare p, aplicaţia g
îndeplineşte relaţia:
|| g ( x ) g ( y) || p || x y || p
Altfel spus, aplicaţia este o contracţie pe domeniul V .

3.

METODE NUMERICE – curs 8
soluţie generală de alegere a funcţiei de iterare, g :
x g( x )
se rescrie ecuaţia (1)
astfel încât
f ( ) 0 g ( )
criteriu general de stop al metodei iterative:
|| x
[s ]
x
[ s 1]
|| p x
sau
|| f ( x ) || p f
[s ]
6.2 Rezolvarea ecuaţiilor algebrice neliniare
fie ecuaţia neliniară:
f (x) 0
(3)
V {x / | x | h , h 0}, , h
- o soluţie
- o vecinătate a soluţiei
6.2.1 Metoda iterării
ecuaţia (3) se rescrie, prin rearanjare convenabilă, sub forma:
exemplu:
3 x sin( x ) e x
x g( x )
(4)
f ( x ) 3 x sin( x ) e x
rearanjare
g( x )
e sin( x )
3
x
e x sin( x )
x
3
x ln(3 x sin( x ))
g ( x ) ln(3 x sin( x ))

4.

METODE NUMERICE – curs 8
- plecând de la un vector iniţial (estimaţie iniţială)
x1 g ( x 0 ), x 2 g ( x1 ),
x 0 V se construieşte şirul:
x k 1 g ( x k ), k 0, 1, ...
Algoritmul care descrie metoda iterării :
* defineşte funcţiile f şi g
citeşte x , f
citeşte x 0
atribuie x n x 0
atribuie flag 1
cât timp ( flag 1 ) execută
atribuie x v x n
atribuie x n g ( x v )
dacă ( | x n x v | x ) sau ( | f ( x n ) | f ) atunci
scrie ‘soluţie x = ’, x n
scrie ‘f(x) = ‘, f ( x n )
atribuie flag 0
(5)

5.

METODE NUMERICE – curs 8
Observaţie:
- alegerea funcţiei g
viteze diferite de convergenţă
punct de start din vecinătatea unei soluţii
convergent către o altă soluţie a ecuaţiei neliniare
divergent
determinarea vecinătăţii unei soluţii:
reprezentarea grafică a funcţiei y f ( x )
interval unde f îşi schimbă semnul
reprezentarea grafică a funcţiilor y x şi y g ( x )
interval unde se intersectează
Propoziţie:
Fie ecuaţia neliniară (1) rescrisă sub forma(2), care admite soluţia . Fie V o vecinătate a
soluţiei. Dacă oricare ar fi x V este îndeplinită condiţia:
(6)
| g ( x ) | c 1 ,
atunci şirul {x k }k 0 , x 0 V , definit de (5), converge către soluţia pentru k .

6.

METODE NUMERICE – curs 8
Observaţii:
1. De multe ori este greu de evaluat derivata funcţiei g pentru a constata îndeplinirea condiţiei
(6). Practic, se poate verifica aceasta pe baza şirului de valori x 0 , x 1 , . Astfel, ţinând cont de
relaţia de recurenţă (5), dacă sunt îndeplinite condiţiile: | x 1 x 0 | | x 2 x 1 | , atunci rezultă
că funcţia g este o contracţie.
2. Dacă | g ( x ) | 1 , este posibil ca şirul de aproximaţii ale soluţiei să fie divergent.
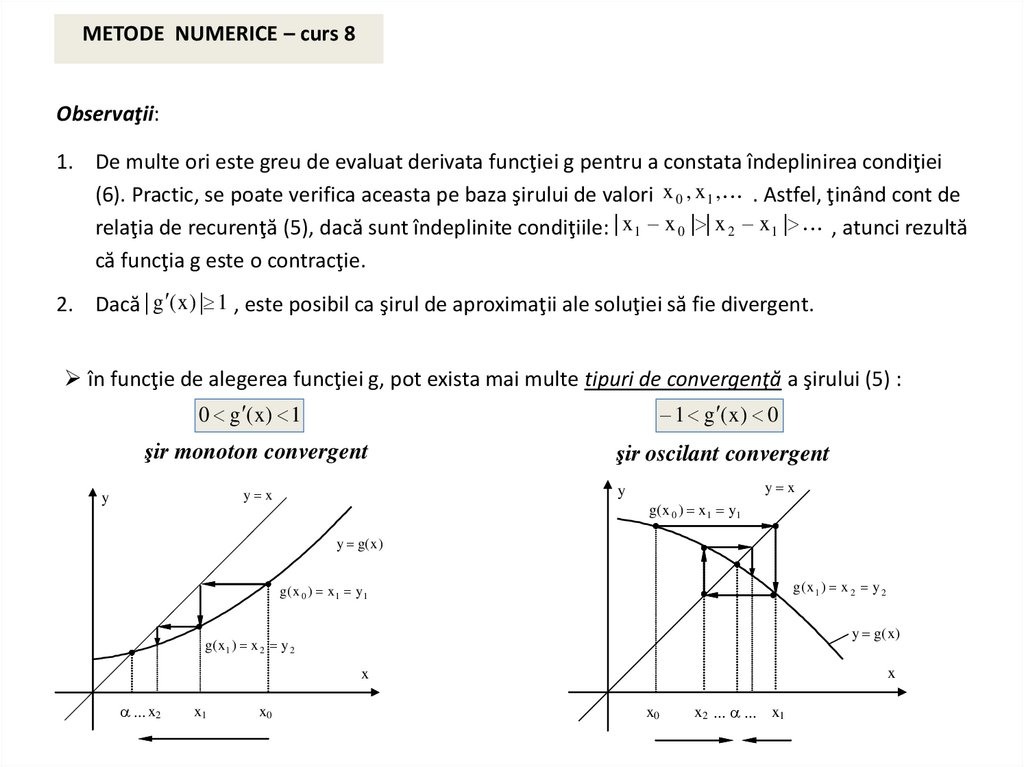
în funcţie de alegerea funcţiei g, pot exista mai multe tipuri de convergenţă a şirului (5) :
0 g ( x ) 1
1 g ( x ) 0
şir monoton convergent
y x
y
y x
y
şir oscilant convergent
g( x 0 ) x 1 y1
y g( x )
g( x 1 ) x 2 y 2
g( x 0 ) x 1 y1
y g( x )
g( x 1 ) x 2 y 2
x
x
... x2
x1
x0
x0
x2 ... ... x1

7.

METODE NUMERICE – curs 8
y g( x )
y
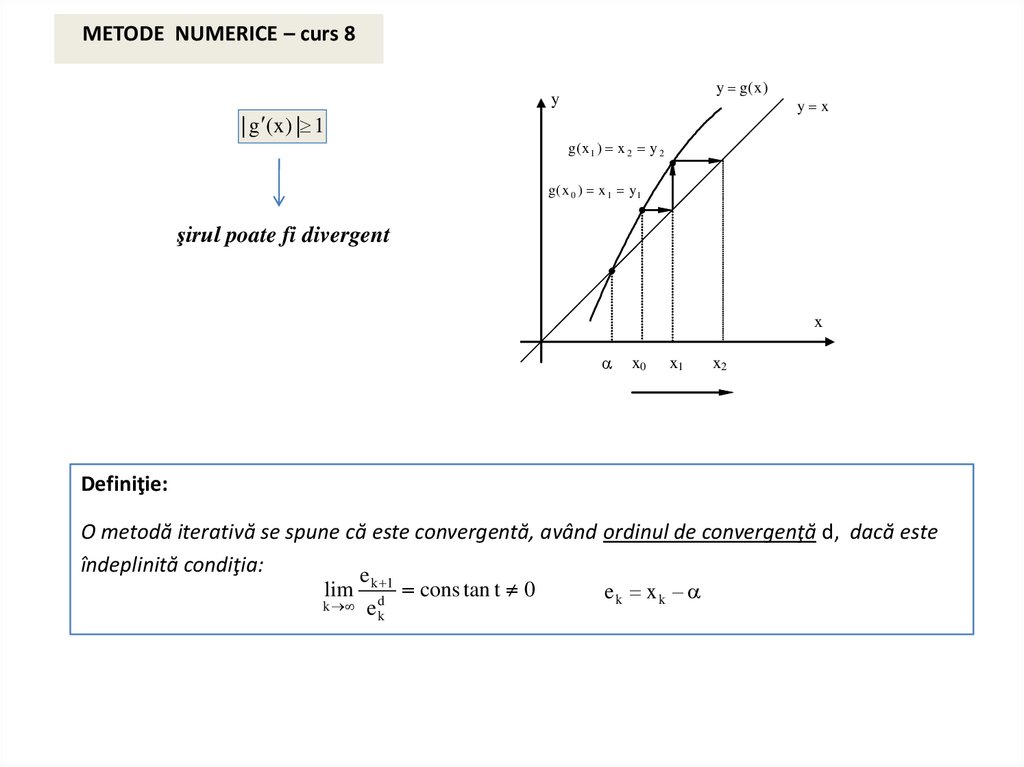
| g ( x ) | 1
y x
g( x 1 ) x 2 y 2
g( x 0 ) x 1 y1
şirul poate fi divergent
x
x0
x1
x2
Definiţie:
O metodă iterativă se spune că este convergentă, având ordinul de convergenţă d, dacă este
îndeplinită condiţia:
e
lim kd 1 cons tan t 0
ek x k
k e
k

8.

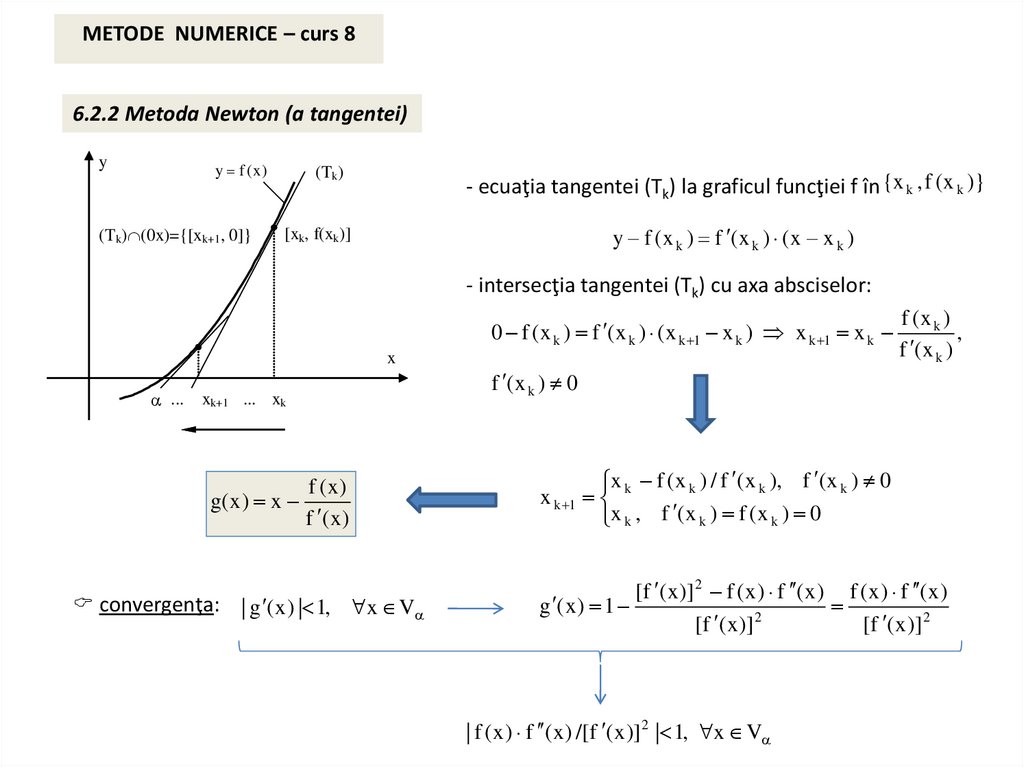
METODE NUMERICE – curs 8
6.2.2 Metoda Newton (a tangentei)
y
y f ( x)
(Tk) (0x)={[xk+1, 0]}
(Tk)
- ecuaţia tangentei (Tk) la graficul funcţiei f în {x k , f ( x k )}
y f ( x k ) f ( x k ) ( x x k )
[xk, f(xk)]
- intersecţia tangentei (Tk) cu axa absciselor:
0 f ( x k ) f ( x k ) ( x k 1 x k ) x k 1 x k
x
...
xk+1 ... xk
f (x)
g( x ) x
f ( x )
convergenţa: | g ( x ) | 1, x V
f (x k )
,
f ( x k )
f ( x k ) 0
x f ( x k ) / f ( x k ), f ( x k ) 0
x k 1 k
x k , f ( x k ) f ( x k ) 0
[f ( x )] 2 f ( x ) f ( x ) f ( x ) f ( x )
g ( x ) 1
[f ( x )] 2
[f ( x )] 2
| f ( x ) f ( x ) /[f ( x )] 2 | 1, x V

9.

METODE NUMERICE – curs 8
Algoritmul care descrie metoda Newton :
* defineşte funcţiile f şi f’
citeşte x , f
citeşte x 0
atribuie x n x 0
atribuie flag 1
cât timp ( flag 1 ) execută
atribuie x v x n
dacă [f ( x v ) 0] şi [f ( x v ) 0] atunci
atribuie x n x v f ( x v ) / f ( x v )
dacă ( | x n x v | x ) sau ( | f ( x n ) | f ) atunci
scrie ‘soluţie x = ’, x n
scrie ‘f(x) = ‘, f ( x n )
atribuie flag 0

10.

METODE NUMERICE – curs 8
Observaţii:
dacă metoda Newton se poate aplica, atunci aceasta are ordinul de convergenţă doi
la fiecare iteraţie numărul de cifre zecimale exacte ale soluţiei se dublează
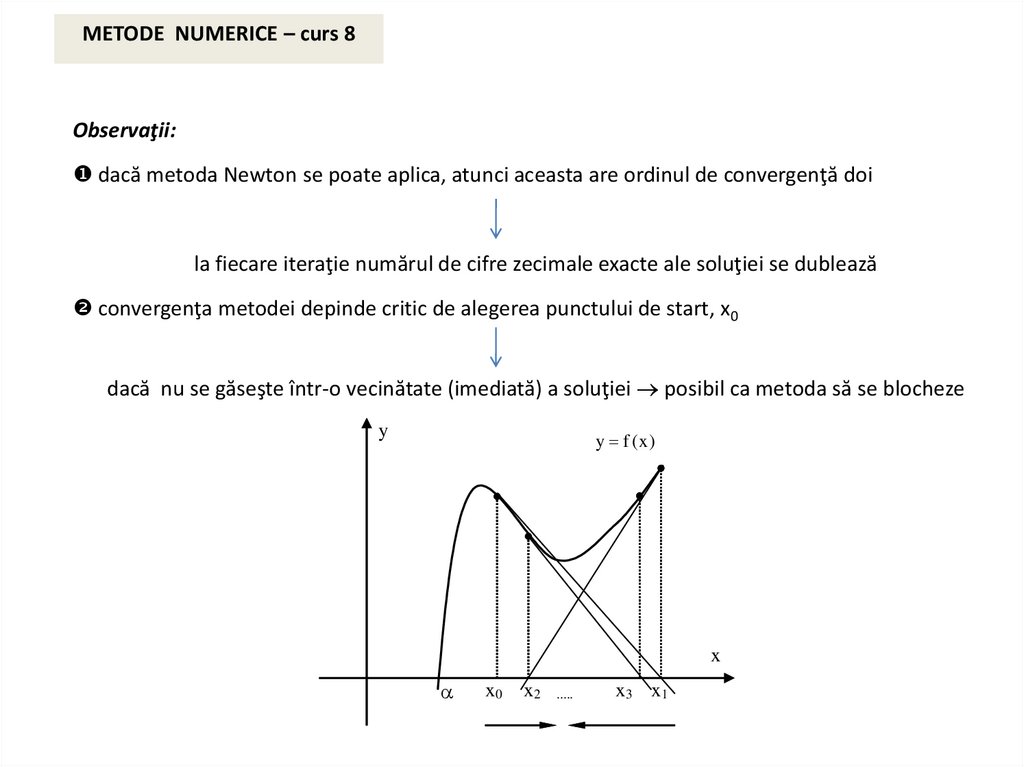
convergenţa metodei depinde critic de alegerea punctului de start, x0
dacă nu se găseşte într-o vecinătate (imediată) a soluţiei posibil ca metoda să se blocheze
y
y f (x)
x
x0
x2
.....
x3 x1

11.

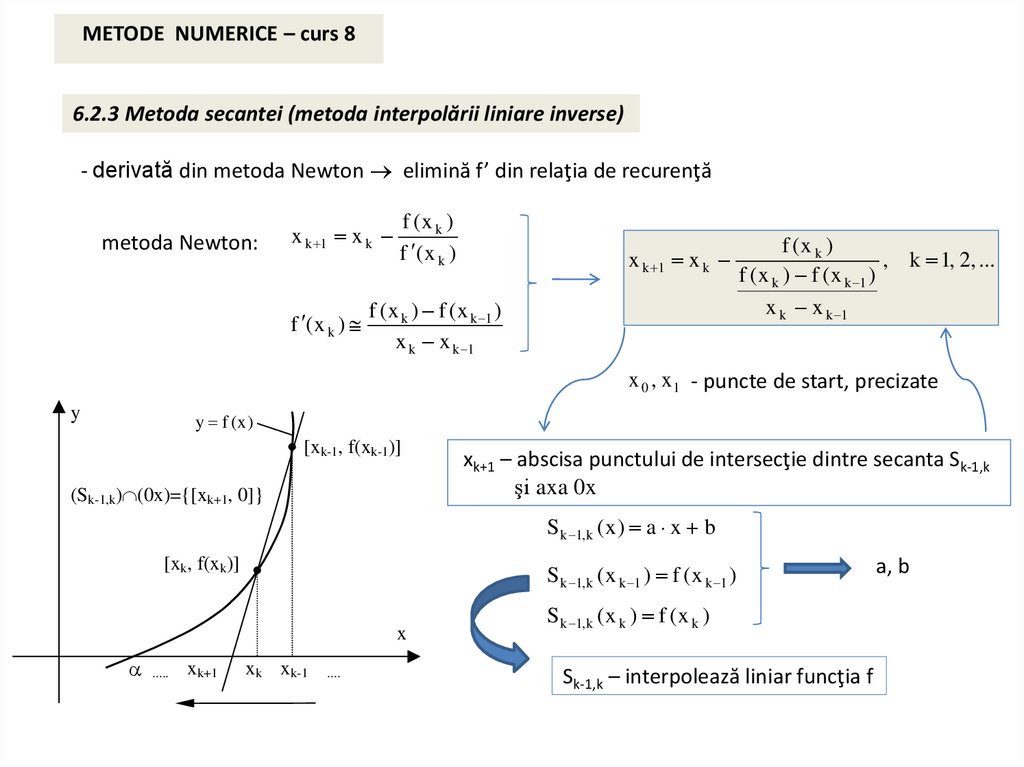
METODE NUMERICE – curs 8
6.2.3 Metoda secantei (metoda interpolării liniare inverse)
- derivată din metoda Newton elimină f’ din relaţia de recurenţă
metoda Newton:
x k 1 x k
f ( x k )
f (x k )
f ( x k )
x k 1 x k
f ( x k ) f ( x k 1 )
x k x k 1
f (x k )
, k 1, 2, ...
f ( x k ) f ( x k 1 )
x k x k 1
x 0 , x 1 - puncte de start, precizate
y
y f (x)
[xk-1, f(xk-1)]
(Sk-1,k) (0x)={[xk+1, 0]}
xk+1 – abscisa punctului de intersecţie dintre secanta Sk-1,k
şi axa 0x
S k 1,k ( x ) a x b
[xk, f(xk)]
S k 1,k ( x k 1 ) f ( x k 1 )
x
.....
xk+1
xk xk-1
....
S k 1,k ( x k ) f ( x k )
Sk-1,k – interpolează liniar funcţia f
a, b

12.

METODE NUMERICE – curs 8
Algoritmul care descrie metoda secantei :
* defineşte funcţiile f
citeşte x , f
citeşte x 1 , x 2
atribuie flag 1
cât timp ( flag 1 ) execută
atribuie x 0 x 1
atribuie x 1 x 2
atribuie x 2 x 1 f ( x 1 ) /{[f ( x 1 ) f ( x 0 )] /( x 1 x 0 )}
dacă ( | x 2 x1 | x ) sau ( | f ( x 2 ) | f ) atunci
scrie ‘soluţie x = ’, x 2
scrie ‘f(x) = ‘, f ( x 2 )
atribuie flag 0

13.

METODE NUMERICE – curs 8
Observaţii:
viteza de convergenţă depinde de gradul în care funcţia f poate fi aproximată prin segmente de
dreaptă cu cât curbura funcţiei f(x) este mai mare, cu atât viteza de convergenţă este mai mică
ordinul de convergenţă al metodei secantei este d ( 5 1) / 2 1.68
6.2.4 Metoda Müller (a interpolării cuadrice inverse)
- metoda Müller extinde rezultatele obţinute la metoda secantei
- funcţia f este aproximată printr-un polinom de gradul al doilea metoda interpolării cuadrice inverse
- necesită 3 puncte de start: x 0 , x1 , x 2 care se află în relaţia:
x 2 x 0 x1
- polinomul de gradul 2 aproximant:
T2 ( x ) a x 2 b x c, a , b, c
a , b, c
T2 ( x i ) f ( x i ), i 0, 1, 2
una din rădăcini, x r o nouă aproximaţie a lui

14.

METODE NUMERICE – curs 8
- optimizarea calculelor se translează sistemul de axe x0y în punctul ( x 0 , 0)
= T2( ) = a 2 + b + c
y
h2 x0 x2
[x1, f(x1)]
h1 x1 x 0
- în sistemul de coordonate translat 0 :
y f (x)
[x0, f(x0)]
xr
x2
T2 (0) f ( x 0 ) f 0
x x0
T2 ( h 2 ) f ( x 2 ) f 2
T2 (h 1 ) f ( x 1 ) f 1
x
x0
c f 0
2
a h 1 b h 1 c f 1
a h 2 b h c f
2
2
2
x1
[x2, f(x2)]
- se reţine rădăcina mai apropiată de centrul sistemului de coordonate 0 (cu modulul mai mic):
2
c
a 1
c
b b2 4 a c
a
2 a
“+” - b<0
“ - ” - b>0
xr x0
2 c
b b2 4 a c
2 c
b b2 4 a c

15.

METODE NUMERICE – curs 8
Algoritmul care descrie metoda Müller :
* defineşte f
citeşte x 0 , x 1 , x 2
Avantaj:
- nu cere existenţa derivatelor lui f
- ordin de convergenţă de 1.85
* ordonează x 2 x 0 x 1
atribuie
xr x0
cât timp | f ( x r ) | r execută
* evaluează f ( x i ), i 0, 1, 2
* calculează a, b, c
* calculează x r
dacă ( x r x 0 ) atunci
altfel
scrie ‘soluţie = ‘, x r
( x 0 , x r , x 1 )
* rearanjează în ( x 2 , x 0 , x 1 )
x 2 x 0 x1
( x 2 , x r , x 0 )
* rearanjează în ( x 2 , x 0 , x 1 )
x x x
2
0
1