Исследование динамической системы по временной реализации

1. ИССЛЕДОВАНИЕ ДИНАМИЧЕСКОЙ СИСТЕМЫ ПО ВРЕМЕННОЙ РЕАЛИЗАЦИИ

Теоретически теория и практика - одно и то же, но
практически -это совсем разные вещи

2.

Анализ реализации
Пусть мы имеем записанную реализацию x = x(t) или, при наличии
дискретизации, временной ряд xk = x(kΔt),
k = 0, 1, 2, ... , М , и пусть
зависимость от времени визуально выглядит сложной и непериодической.
Можно ли из ее анализа заключить, произведена ли реализация
динамической системой или это просто случайный шумовой сигнал?
Если это динамическая система, то что можно сказать о ее
свойствах и характеристиках — сколько переменных необходимо для
задания состояния, какова фрактальная размерность аттрактора,
отвечающего за наблюдаемый режим, хаотический ли он, можно ли
сконструировать модель в виде дифференциальных уравнений или
отображений,
которая
позволяла
бы
адекватно
воспроизвести
наблюдаемую временную зависимость и прогнозировать будущее
состояние системы?

3. РЕКОНСТРУКЦИЯ АТТРАКТОРА

Главная идея применения методов хаотической динамики к
анализу временных рядов состоит в том, что основная структура
хаотической системы, содержащая в себе всю информацию о
системе, а именно аттрактор динамической системы, может быть
восстановлена через измерение только одной наблюдаемой этой
динамической системы, фиксированной как временной ряд.
Процедура реконструкции фазового пространства и восстановление
хаотического аттрактора системы при динамическом анализе
временного ряда сводится к построению псевдофазового
пространства.

4. РЕКОНСТРУКЦИЯ АТТРАКТОРА Теорема Уитни-Такенса.

Пусть M – компактное d-мерное многообразие класса C2, в котором
существует аттрактор динамической системы). Отображение F
F: M RD:
определяемое как
F (t ) [ i (t ), i (t ),..., i (t 2 N )] ,
где i (t n ) - i-я компонента траектории системы, а >0 - период
дискретизации, есть диффеоморфизм для почти любого 0 и D > 2d
.
Данная теорема дает предпосылки для реконструкции аттрактора
динамической системы по одной временной реализации.
.

5. РЕКОНСТРУКЦИЯ АТТРАКТОРА

АТТРАКТОР ЧУА
АТТРАКТОР ЛОРЕНЦА

6. РЕКОНСТРУКЦИЯ АТТРАКТОРА. ВЫБОР 

РЕКОНСТРУКЦИЯ АТТРАКТОРА. ВЫБОР
( x k ) ( x (k 1) )
Если
слишком
мало,
выполняется
и
восстановленный
аттрактор
оказывается ограниченным областью вблизи диагонали
пространства, в котором производится восстановление.
Если же значение слишком велико, а система является
хаотической, то значения ( x k ) и ( x (k 1) ) оказываются
некоррелированными (в пределах точности, определяемой
производимыми вычислениями), и структура аттрактора
исчезает.
Если же значение оказывается слишком близким к значению
какого-либо периода системы, то та составляющая, которая
характеризуется указанным периодом, при восстановлении будет
представлена недостаточно полно.
Считается наиболее оптимальным значение T / 4 , где Т некоторый характерный временной период рассматриваемого
сигнала.
i
значение
i
i
i

7. РЕКОНСТРУКЦИЯ АТТРАКТОРА. ВЫБОР 

РЕКОНСТРУКЦИЯ АТТРАКТОРА. ВЫБОР
АТТРАКТОР ЛОРЕНЦА
=0.05 (а)
=0.15 (б)
=0.5 (в)
=0.75 (г).

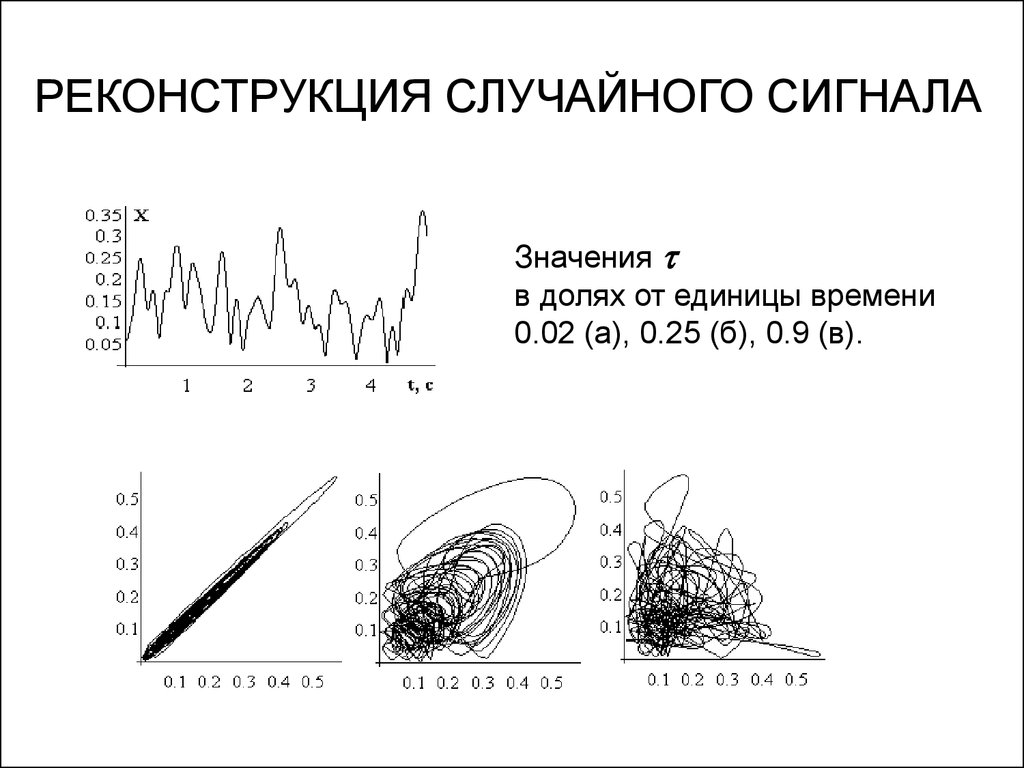
8. РЕКОНСТРУКЦИЯ СЛУЧАЙНОГО СИГНАЛА

Значения
в долях от единицы времени
0.02 (а), 0.25 (б), 0.9 (в).

9. РАЗМЕРНОСТЬ ВЛОЖЕНИЯ

Размерность вложения m –
минимальная
целая размерность фазового
пространства, которое
содержит аттрактор.
F (t ) [ x(t ), x(t ),..., x(t m )]

10. ФРАКТАЛЬНАЯ РАЗМЕРНОСТЬ И РАЗМЕРНОСТЬ ВЛОЖЕНИЯ

log N
d lim
0 log 1 /
Если динамическая система, породившая исследуемый сигнал, является конечномерной, а соответствующий аттрактор имеет
либо целую, либо дробную размерность d c , то
начиная как минимум с m 2d c 1 величина
d c не зависит от m . В то же время, как показывает практика], достаточно выбрать
m d.
c

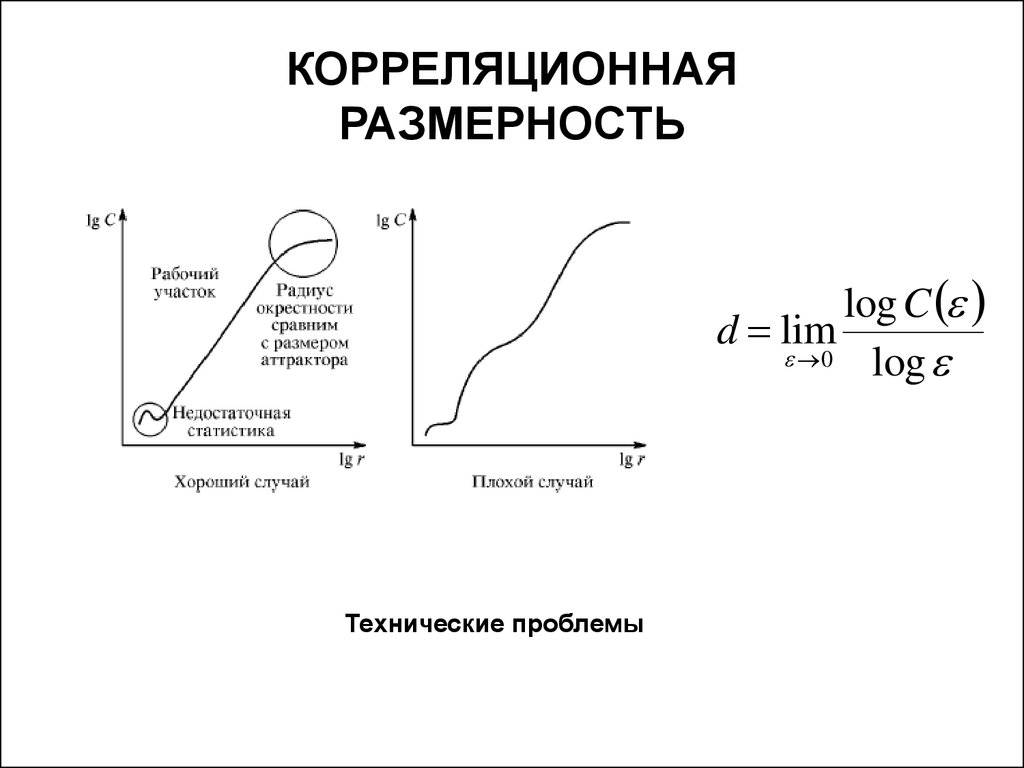
11. КОРРЕЛЯЦИОННАЯ РАЗМЕРНОСТЬ

Аттрактор Энона
КОРРЕЛЯЦИОННАЯ
РАЗМЕРНОСТЬ
При определении d c вычисляются расстояния между парами точек в фазовом пространстве и определяется корреляционный
интеграл C ( ) lim
N
Lij
N
2
, где N -число точек,
Lij - число пар точек (i, j) для которых расстояние Sij .
Зависимость корреляционного интеграла от ε подчиняется степенному закону, т.е.
lim C ( ) const d .
0
Корреляционную размерность d c определяют по наклону графика зависимости С(ε)
от 1/ε в двойном логарифмическом масштабе.

12.

КОРРЕЛЯЦИОННАЯ РАЗМЕРНОСТЬ
При определении корреляционной размерности вычисляются расстояния
между парами точек в фазовом пространстве и определяется корреляционный.
Lij
интеграл C ( ) lim 2 , где N - число точек, Lij - число пар точек (i, j) для
N N
которых расстояние Sij
log C
d lim
0
log

13. КОРРЕЛЯЦИОННАЯ РАЗМЕРНОСТЬ

log C
d lim
0
log
Технические проблемы

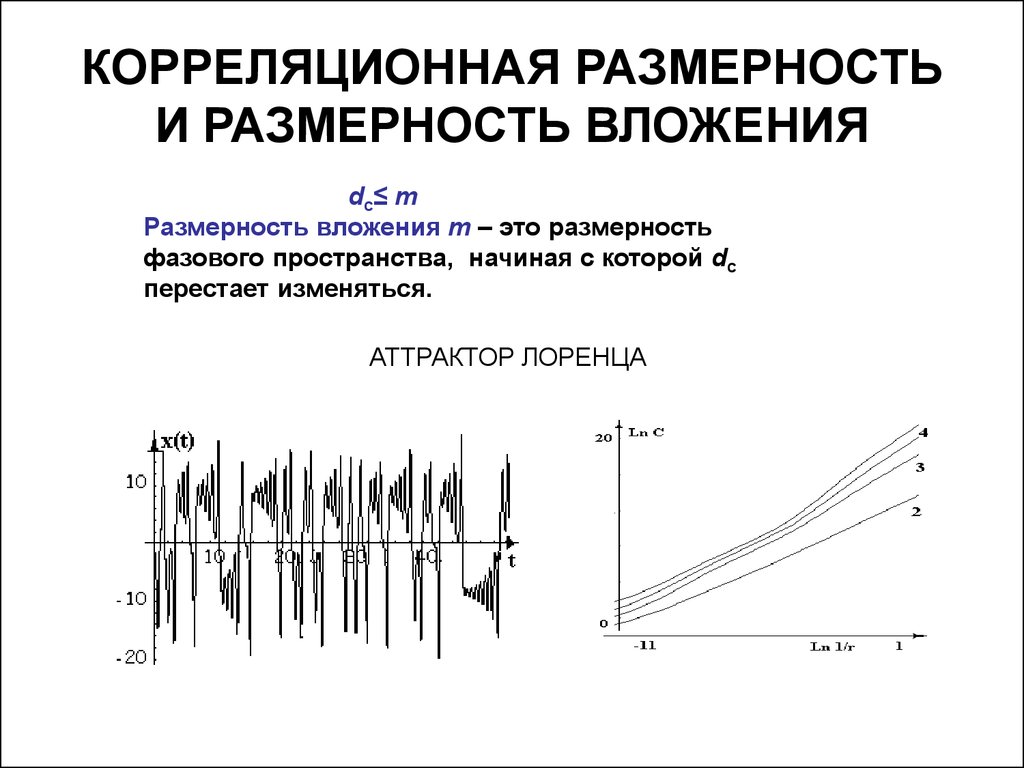
14. КОРРЕЛЯЦИОННАЯ РАЗМЕРНОСТЬ И РАЗМЕРНОСТЬ ВЛОЖЕНИЯ

dc≤ m
Размерность вложения m – это размерность
фазового пространства, начиная с которой dc
перестает изменяться.
АТТРАКТОР ЛОРЕНЦА

15. КОРРЕЛЯЦИОННАЯ РАЗМЕРНОСТЬ И РАЗМЕРНОСТЬ ВЛОЖЕНИЯ

Для случайных процессов, т.е. порожденных системой с большим
числом степеней свободы, фрактальная размерность является целым
числом и ее значение приближенно равняется размерности
фазового пространства, в котором она вычисляется .
Шумовой сигнал

16. ВЫЧИСЛЕНИЕ ПОКАЗАТЕЛЯ ЛЯПУНОВА

d (t k )
1 N
ln
t N t 0 k 1 d 0 (t k 1 )

17. ВЫЧИСЛЕНИЕ ПОКАЗАТЕЛЯ ЛЯПУНОВА

1. Производится реконструкция аттрактора в фазовом пространстве
методом запаздываний и определяется размерность вложения m.
2. Берем за исходную некоторую точку Хо на реконструированном
аттракторе и находим другую точку х0, находящуюся на малом расстоянии
||х0 — х’о|| = εo, но не близкую по времени.
3. Затем отслеживаем шаг за шагом динамику при старте из этих двух
точек. Когда расстояние между изображающими точками x1 и х’1 превысит
некоторую заданную величину εmax, остановимся и зафиксируем период
времени Т1, который для этого понадобился, и отношение конечного и
начального расстояний ε o/εo.
4. Отыскиваем другую точку старта возмущенной траектории. Она должна
быть по возможности близка к точке x1 и сдвинута от нее по направлению,
близкому к направлению вектора х1 — x’1. Пусть это точка х1 и ||х1"—x1||= ε1.
Отслеживаем теперь траектории, стартующие из точек x1 и х1", пока через
некоторый следующий период времени T2 расстояние не
1
k
превысит εmax, и вычисляем отношение ε'1/ ε1.
ln
5. Далее процедура повторяется многократно, и
k
k 0
ляпуновский показатель оценивается как:
’
k 1
k

18.

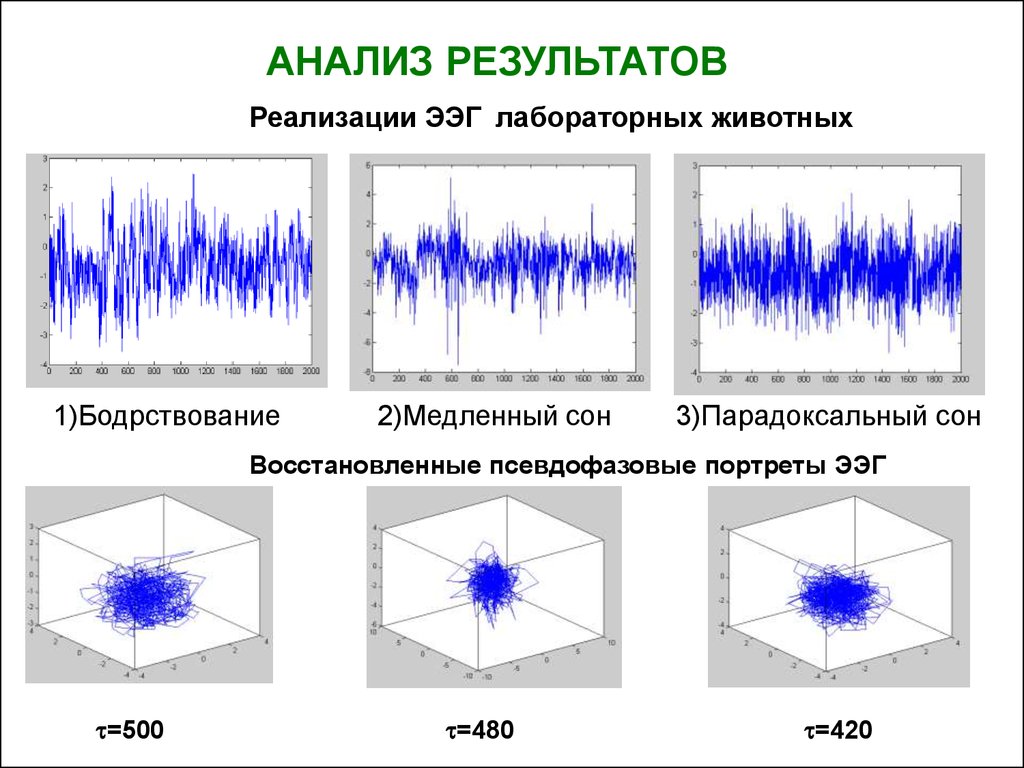
АНАЛИЗ РЕЗУЛЬТАТОВ
Реализации ЭЭГ лабораторных животных
1)Бодрствование
2)Медленный сон
3)Парадоксальный сон
Восстановленные псевдофазовые портреты ЭЭГ
=500
=480
=420

19.

Фазовые портреты изменения величины окна перегрузки узла компьютерной сети

20.

EUR/USD, time frame H1.
NZD/CAD, time frame H4.
GBP/JPY, time frame D1.
CAD/JPY, time frame 1WEEK.

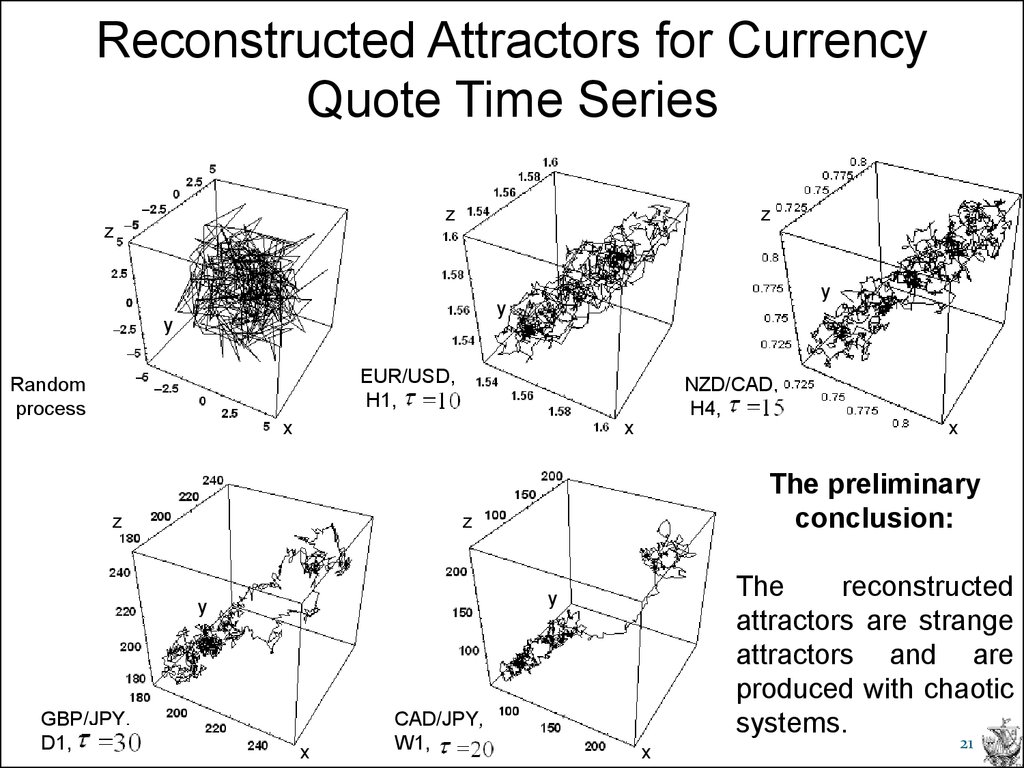
21. Reconstructed Attractors for Currency Quote Time Series

z
z
z
y
y
y
EUR/USD,
H1,
Random
process
NZD/CAD,
H4,
x
x
z
The preliminary
conclusion:
z
The
reconstructed
attractors are strange
attractors and are
produced with chaotic
systems.
y
y
GBP/JPY,
D1,
x
x
CAD/JPY,
W1,
x
21

22. Estimation of the Correlation Dimension for quote time series(1)

Lorenz System,
D(m) =2.03, m=3
Random process
EUR/USD, H1,
D(m)=2.5, m=5
22

23. Estimation of the Correlation Dimension for quote time series(2)

NZD/CAD, H4,
D(m)=2.4, m=3
GBP/JPY, D1,
D(m)=3.5, m=5
CAD/JPY, 1WEEK,
D(m)=3.7, m=4
23

24. Estimation of the Lyapunov Exponent

Lyapunov exponent for the quote time series
Λ
EUR/USD NZD/CAD GBP/JBY
CAD/JPY Lorenz
H1
H4
D1
W1
system
0.37
0.39
0.42
0.4
1.37
24