Похожие презентации:
Рассеяние носителей заряда в неидеальной кристаллической решетке
1. Рассеяние носителей заряда в неидеальной кристаллической решетке
2.
В кинетических явлениях принципиально важную роль играют процессырассеяния носителей заряда на колебаниях кристаллической решетки и ее
дефектах.
В кинетическом уравнении Больцмана информация о рассеянии входит в
интеграл столкновения через вероятность рассеяния носителя в единицу
времени.
Надо рассмотреть задачу: Hужно рассмотреть электрон в кристалле с
колеблющимися атомами и дефектами. Отклонения потенциала решетки от
идеального периодического можно рассматривать как малое возмущение,
которое приводит к переходам электронов между его состояниями в идеальной
решетке (состояниями нулевой задачи). Нужно найти вероятность таких
переходов.
Как правило, интерференцией различных механизмов рассеяния можно
пренебречь. Можно вычислить по отдельности вероятности для каждого
механизма рассеяния и затем их сложить
3.
Рассеяние носителей на колебаниях кристаллической решетки (фононах)Рассмотрим систему, состоящую из электрона и колеблющихся атомов решетки.
Гамильтониан такой системы
Hˆ Hˆ 0e Hˆ 0ph Hˆ e ph
e - Гамильтониан электрона в идеальной неподвижной решетке (блох. Гам.)
ˆ
H0
ph - Гамильтониан фононов
ˆ
H
0
Hˆ 0ph
- Гамильтониан электрон-фононного взаимодействия (изменение
энергии системы вследствие взаимодействия электронов с
колебаниями решетки)
Как правило, основной вклад дает взаимодействие электронов с
длинноволновыми фононами λ=2π/q>>a => можно перейти к концепции
непрерывной среды, определив смещение u(r). Для этого нужно в полученных
ранее выражениях для смещений атомов заменить вектор трансляции на
радиус-вектор
4.
Взаимодействие с длинноволновыми акустическими фононами;Метод потенциала деформации
u(r )
1
NM
ξ q, s exp iqr Q(q, s ) exp iqr Q* (q, s )
q,s
1
p q, s
Q q, s x q, s
2
i q, s
Электрон фононное взаимодействие возникает вследсвтие отклонения атомов
u
от положения равновесия H e ph u ,
,
x
Колебания малые можно разложить в ряд Тейлора
u
u
1
H e ph u ,
,
H
(
0
)
A
u
E
e ph
,
2 ,
x
x
Если нет ни смещения , ни деформации H e ph 0 H e ph (0) 0
5.
uu
1
H e ph u ,
,
A
u
E
,
2 ,
x
x
Длинноволновые акустические колебания ячейка колеблется как целое
при бесконечно длинной волне отвечает смещение кристалла как целого
При смещении кристалла как целого энергия системы не изменяется
должен быть предельный переход H e ph 0.
При u const 0 и
u
0
x
Предельный переход H e ph 0 имеет место, только если A 0
H e ph E ,
,
u(r )
1
NM
u
x
ξ q, s exp iqr Q(q, s ) exp iqr Q * (q, s )
q,s
Каждое дифференци рование дает умножение на q.
q 0 членами , содержащими производные u порядка , выше первого
можно пренебречь
6.
H e ph E ,,
u
потенциал деформации
x
E , тензор постоянных деформационного потенциала
)
( асим)
Представим тензор E , в виде суммы симметричного E ( сим
тензоров
, и асимметричного E ,
)
( асим)
E , E ( сим
, E ,
H e ph
1
1
)
E , E , ; E ( асим
E , E ,
,
2
2
)
( aсси )
( сим )
( сим ) u
( aсси )
( aсси ) u
H e( сим
H
;
H
E
;
H
E
, x e ph , , x
ph
e ph
e ph
,
)
E ( сим
,
Асимметричный тензор всегла можно записать через тензорный символ Кронекера , , и
компоненты псевдовектора A как
)
E ( aсси
, , A
,
)
H e( aсси
ph , , A
,
u
u
A , , A rotu A rotu
x
x
,
При повороте кристалла как целого
rotu const 0
)
E ( aсси
0
,
H
0
e ph
E , симметричный тензор E , E ,
7.
H e ph E ,,
u 1
u 1
u
E ,
E ,
x 2 ,
x 2 ,
x
u
u
1
1
E ,
E ,
E , E ,
2 ,
x
2 ,
x
u
1
E ,
2 ,
x
H e ph E , , ; ,
,
1 u u
2 x x
В изотропном случае E ,
тензор деформации
E1 , , E1 постоянная потенциала деформации
H e ph E , , E1 , E1
,
u
E1divu
x
V
divu
относительно изменение объема эл. ячейки
V0
E1 изменение энергии при изменении объема элем. ячейки в два раза
8.
В проведенных выше рассуждениях мы фиксировали ветвь. С учетом трехветвей акустических колебаний
3
H e ph E , ( s )
s 1
u( s )
1
NM
u ( s )
x
H e ph
Hˆ e ph
i
NM
ξ q, s exp iqr Q(q, s ) exp iqr Q * (q, s )
q
i
NM
i
NM
u ( s )
;
x
ξ q, s q exp iqr Q(q, s ) exp iqr Q * (q, s )
q
E ξ q exp iqr Q(q, s) exp iqr Q (q, s)
3
*
s 1 q
,
3
ˆ (q, s ) exp iqr Qˆ (q, s )
E
ξ
q
exp
i
qr
Q
,
s 1 q
bˆ(q, s ); Qˆ (q, s )
bˆ (q, s )
2 (q, s )
2 (q, s )
Qˆ (q, s )
3
Hˆ eак ph i E , ξ q
s 1 q ,
exp iqr bˆ(q, s ) exp iqr bˆ (q, s )
2 NM (q, s )
9.
3Hˆ eак ph i Hˆ eак ph (q, s )
s 1 q
exp iqr bˆ(q, s ) exp iqr bˆ (q, s )
2 NM (q, s )
Hˆ eак ph (q, s ) E , ξ q
,
В изотропном случае E , E1 ,
E ξ q E ξ q E ξq
,
1
1
,
Hˆ eак ph (q, s ) E1ξq
exp iqr bˆ(q, s ) exp iqr bˆ (q, s )
2 NM (q, s )
Поперечные фононы ( s 2,3) ξq 0 нет рассеяния на поперечных фононах
В изотропном случае есть рассеяние только на продольных акустических фононах
В анизотропном случае появляется рассеяние так же и на акустических фононах
10.
Взаимодействие носителей заряда с оптическими фононами вгомеополярном кристалле; метод потенциала деформации
Гомеополярный кристалл – атомы не обладают зарядом.=> рассеяние
происходит на деформационном потенциале оптических колебаний
H e ph A u
u
1
E
,
2 ,
x
В длинноволновых оптических колебаниях центр тяжести элементарной
ячейки остается неподвижным при , u 0
H e ph A u
Для электронов вблизи минимума A E ( 0, ) n
n единичный вектор вдоль оси, идущей из центра зоны Бриллюэна в
рассматриваемый минимум
Hˆ
ак
e ph
3
i Hˆ eак ph (q, s )
s 1 q
, непол
(0)
Hˆ eопт
(
q
,
s
)
E
, ξ n
ph
,
exp iqr bˆ(q, s ) exp iqr bˆ (q, s )
2 NM (q, s )
11.
Взаимодействие носителей заряда с оптическими фононами вгетерополярном кристалле. Поляризационное рассеяние
В гетерополярном полупроводнике атомы решетки обладают отличными от нуля
эффективными зарядами. При оптических колебаниях решетка деформируется
=> возникает дополнительный дипольный момент ячейки d => возникает
дополнительная поляризация среды P=> возникает дополнительное
электрическое поле φ, действующее на электрон
, поляр
H eопт
e (r )
ph
(r )
cв P
P
d
V0
4
cв
4
(r )
d
V0
12.
Рассмотрим гетерополярный кристалл с элементарной ячейкой, содержащей дваатома различной природы (шелочно-галоидные кристаллы - NaCl,KCl и др.,
кристаллы типа CsCl, соединения AIIIBV-InSb,GaAs и т.д. ). Ze и –Ze –
эффективные заряды первого и второго атомов. Если связь в кристалле – не
чисто ионная, то Z – дробное.
Дипольный матричный элемент ячейки
d eZ u1 (r ) u 2 (r ) u j (r )
d
eZ
NM
d
1
NM
ξ j q, s exp iqr Q(q, s ) exp iqr Q * (q, s )
q,s 4
*
ξ
ξ
exp
i
qr
Q
(
q
,
s
)
exp
i
qr
Q
(q, s )
1
2
q,s 4
ieZ
NM
*
ξ
q
ξ
q
exp
i
qr
Q
(
q
,
s
)
exp
i
qr
Q
(q, s )
1
2
q,s 4
При длинноволновых оптических колебаниях положение центра тяжести
элементарной ячейки практически не изменяется
M j ξ j (0, s) 0 M 1ξ1 (0, s) M 2ξ 2 (0, s) 0 ξ 2 (0, s)
j
e1 ( s )
M1
ξ1 (0, s )
M2
ξ1 (0, s )
единичн. вектор в направлении смещения первого атома
ξ1 (0, s )
ξ1 (0, s ) ξ1 (0, s )e1 ( s ); ξ 2 (0, s )
M1
ξ1 (0, s )e1 ( s )
M2
13.
M1ξ1 (0, s ) ξ1 (0, s )e1 ( s ); ξ 2 (0, s )
ξ1 (0, s )e1 ( s )
M2
Условие ортонормировки амплитуд собственных колебаний
M ξ
j
j
(q, s ) ξ j (q, s1 ) M s , s1
j
ξ j (0, s1 ) ξ j (0, s ) M j ξ j (q, s ) M
2
j
M1
M 1 1 (0, s ) M 2 2 (0, s ) M 1 M 2 ξ 2 (0, s )
ξ1 (0, s )e1 ( s )
M2
2
2
2
M1
2
M 1 1 (0, s ) M 2
1 (0, s ) M 1 M 2 1 (0, s )
M2
2
ξ1 (0, s )
M2
M1
e1 ( s ); ξ 2 (0, s )
e1 ( s )
M1
M2
M2
M1
14.
ieZNM
d
ξ1 (0, s )
*
ξ
q
ξ
q
exp
i
qr
Q
(
q
,
s
)
exp
i
qr
Q
(q, s )
1 2
q,s 4
M2
M1
e1 ( s ); ξ 2 (0, s )
e1 ( s )
M1
M2
ieZ
NM
ieZ
N
M1 M 2
qe 1 ( s) exp iqr Q(q, s) exp iqr Q* (q, s)
M 1M 2
d
ieZ
d
q,s 4
NM
M
q,s 4
M
qe 1 ( s) exp iqr Q(q, s) exp iqr Q* (q, s)
M 1M 2
*
qe
(
s
)
exp
i
qr
Q
(
q
,
s
)
exp
i
qr
Q
(q, s )
1
q,s 4
M 1M 2
приведенная масса элементарной ячейки
M1 M 2
15.
ieZd
NM
(r )
*
qe
(
s
)
exp
i
qr
Q
(
q
,
s
)
exp
i
qr
Q
(q, s )
1
q,s 4
4 ieZ
V0
exp
i
qr
qe
(
s
)
Q
(
q
,
s
)
exp
i
qr
qe
(
s
)
Q
(
q
,
s
)
1
1
NM q
s 4
s 4
(r ) A(q) exp iqr
q
(r ) (r )
*
A
(
q
)
A
( q) exp iqr 0
A (q) exp iqr A ( q) exp iqr
q
*
q
*
q
A( q) A* (q)
(r ) A(q) exp iqr
q
1
1
A
(
q
)
exp
i
qr
A(q) exp iqr
2 q
2 q
A(q)
1
1
A (q)
A(q) exp iqr A( q) exp iqr
exp iqr
exp iqr
2 q
2 q
2
q 2
16.
4 ieZ(r )
V0 NM
exp iqr qe (s) Q(q, s) exp iqr qe (s) Q (q, s)
s 4
q
1
s 4
(r ) (q) exp iqr (q) exp iqr
1
q
q (q) exp iqr q
2
2
(q) exp iqr
q
(q)
4 ieZ
V0
(r )
q,s 4
H
опт, поляр
e ph
1
2
NM q
4 ieZ
V0 NM
e (r )
4 ieZ
V0
exp
i
qr
qe
(
s
)
Q
(
q
,
s
)
exp
i
qr
qe
(
s
)
Q
(
q
,
s
)
q
1
1
s 4
s 4
qe (s) Q(q, s)
1
s 4
qe 1 ( s) Q(q, s) exp iqr Q (q, s) exp iqr
q2
4 ie 2 Z
V
q,s 4
0
NM
qe 1 ( s) Q(q, s) exp iqr Q (q, s) exp iqr
q2
17.
Hˆопт, поляр
e ph
Qˆ (q, s)
Hˆ
опт, поляр
e ph
4 ie 2 Z
V
q,s 4
0
NM
qe 1 (s) Qˆ (q, s) exp iqr Qˆ (q, s) exp iqr
q2
; Qˆ (q, s)
bˆ (q, s )
2 (q, s)
2 (q, s)
4 iZe 2
q , s 4 V0
qe 1 (s) exp iqr bˆ(q, s) exp iqr bˆ (q, s)
2 (q, s) NM
q2
Поперечные фононы q e1 ( s) qe 1 ( s) 0
Поляроное рассеяние происходит только на продольных фононах ( s 4)
Продольные фононы q || e1 ( s) qe 1 ( s ) q
Hˆ
опт, поляр
e ph
4 iZe 2
V0
q
1
exp iqr bˆ(q, s 4) exp iqr bˆ (q, s 4)
2 4 (q) NM q
В гетерополярных кристаллах полярное рассеяние, как правило, существенно
сильнее деформационного. Причина – силы, возникающие в результате
поляризационного взаимодействия, являются дальнодействующими. В результате
на электрон оказывает влияние изменение дипольного момента одновременно во
многих ячейках.













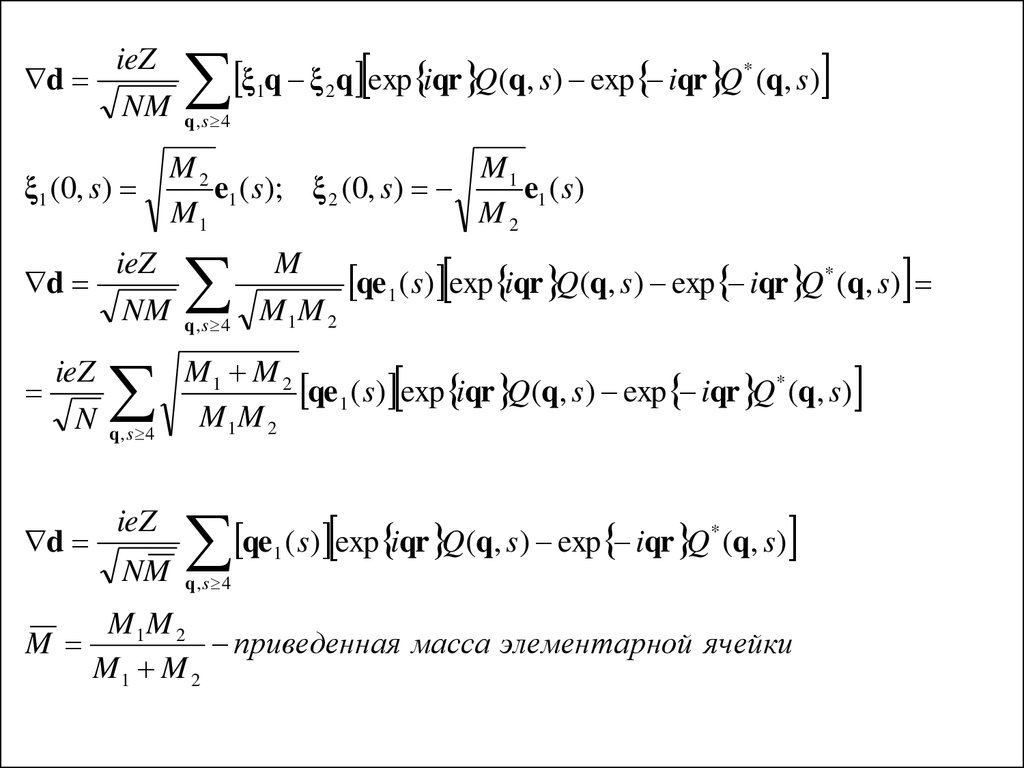
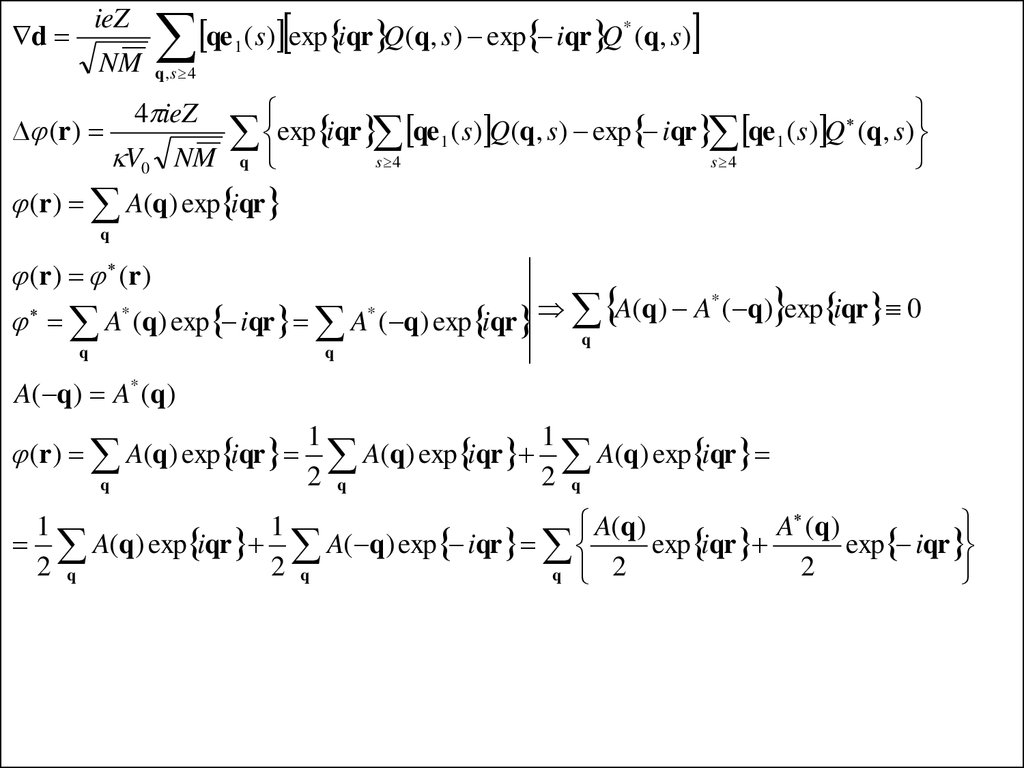


 Физика
Физика








