Похожие презентации:
Колебания кристаллической решетки
1. Колебания кристаллической решетки.
Гармоническое приближение2.
Адиабатическое приближение; me<<M => можно считать, что электроннаяподсистема успевает подстраиваться под мгновенное положение ядер
(атомных остовов)=>движение ядер можно рассматривать в эффективном
среднем поле, создаваемом электронами (рассчитывается в предположении
неподвижных ядер)
pi2
H
U (R1 , , R i , , R N ); R i R i( 0) u i
i 1 2 M i
N
1) Амплитуда смещения атомов << расстояния между ними => потенциальную
энергию кристаллической решетки можно разложить в ряд Тейлора в
окрестности равновесных положений атомов
U R i U R
U R i( 0)
Fi ,
U
Ri ,
(0)
i
U
1
2U
ui ,
ui , u j ,
2 i , j Ri , R j ,
i , Ri ,
0
,
0
- Константа для данного кристалла (берем за начало отсчета энергии)
0
0
проекция на ось силы, действующей в положении равновесия
на i-ый атом со стороны всех остальных
3.
U1
Ai , j, ui , u j ,
2 i, j
,
Оставляем только первый неисчезающий член – квадратичный (гармоническое
приближение)
U
1
Ai , j, ui , u j , положительно определенная квадратичная форма Ai ,i, 0
2 i, j
,
pi2 1
H
Ai , j, ui , u j ,
2 i, j
i 1 2 M i
N
- система взаимодействующих ЛГО
,
Переходим к нормальным координатам (обязательно при этом учитывая
периодичность расположения положений равновесия атомов)
3N
H Hf
f 1
Hf
p 2f
2 1
1 2f x 2f
2
- ЛГО с единичной массой и частотой, равной частоте
нормального колебания
4.
H ;3N
H
f
Hf
f 1
p 2f
2 1
1 2f x 2f
2
x f1 p f p f x f1
p f , x f1
f , f1
x
p
x
p
p f , x f канонически сопряженные :
f2
f2
f2
f2
f2
p f , p f1 x f , x f1 0
pˆ , xˆ pˆ xˆ xˆ pˆ
pˆ , pˆ xˆ , xˆ 0
x f xˆ f
при переходе к кв. описнанию
:
ˆ
p
p
f
f
Hˆ
3N
H
f 1
Hf
p
2 1
f1
f
f1
f
3N
1 x
2
f
2
Hˆ f
2 x f xˆ f
f p f pˆ f
pˆ 2f
f
2 1
pˆ f i
1 2f xˆ 2f
2
x f
В координатном представлении : xˆ f x f ; pˆ f i
f1
f
i 1
Hf
2
f
Hˆ
f
x f
f1
f1
f
f , f1
5.
Hˆ3N
Hˆ f ; Hˆ f
f 1
pˆ 2f
2 1
1 2f x 2f
2
Переменные в УШ разделяются
x f n ( x f ); n ( x)
3N
f 1
f
E n f f n f ; n
3N
f 1
x x
exp 2 H n ;
2
2 n n! 1/ 2
1
n; n - число заполнения осциллятора (число
2
квантов, которые вобрал в себя ЛГО)
Для того, чтобы задать стационарное состояние всей системы осцилляторов
нужно указать число заполнения каждого осциллятора.
Каждому осциллятору (собственному колебанию) поставим в соответствие
квазичастицу с энергией, равной кванту этого осциллятора. Такие квазичастицы
называются фононами. Поставим нашей системе осцилляторов газ таких
фононов так, чтобы число фононов данного типа в газе равнялось числу
заполнения соответствующего осциллятора. Если система осцилляторов
переходит из одного состояния в другое, т.е. меняются числа заполнения
осцилляторов, то соответствующее число фононов рождается и исчезает.
6.
Вместо того, чтобы рассматривать колебания решетки можем рассматривать газиз фононов.
Работаем с газом частиц => удобно перейти в представление вторичного
квантования. Введем операторы уничтожения и рождения фононов
aˆ f n ( x f1 ) f , f1 n n 1 ( x f ); aˆ f n f , f1 n n 1 ( x f1 )
Числа n и n подбираем так, чтобы
Nˆ aˆ f aˆ f оператором числа фононов f оператор числа квантов осциллятора :
Nˆ n n n
Nˆ n aˆ f aˆ f n n aˆ f n 1 n n 1 n
Nˆ n n n
n n
n n 1 n
n n 1
aˆ f n ( x f1 ) f , f1 n n 1 ( x f ); aˆ f n f , f1 n 1 n 1 ( x f1 )
Фононы фермионы или бозоны ? Нужно найти перестановочные соотношения
(для фермионов и бозонов они имеют совершенно определенный вид)
aˆ f aˆ f n ( f ) n n ( f )
aˆ f aˆ f n ( f ) n 1aˆ f n 1 ( f ) n 1 n
[aˆ f , aˆ f ] aˆ f aˆ f aˆ f aˆ f 1
7.
Фононы фермионы или бозоны ? Нужно найти перестановочные соотношения(для фермионов и бозонов они имеют совершенно определенный вид)
aˆ f aˆ f n ( f ) n n ( f ) aˆ f aˆ f x f aˆ f aˆ f n f ( f1 ) n f ( f1 ) aˆ f aˆ f n f ( f ) n f x f
f1
1
1
f1 f
aˆ f aˆ f n ( f ) n 1aˆ f n 1 ( f ) n 1 n aˆ f aˆ f x f aˆ f aˆ f n f ( f1 )
f1
n f ( f1 ) aˆ f aˆ f n f ( f ) (n f 1) x f
f1 f
1
1
[aˆ f , aˆ f ] aˆ f aˆ f aˆ f aˆ f 1
f1 f 2
aˆ f1 aˆ f 2 x f aˆ f1 aˆ f 2 n f ( f ) n f ( f ) aˆ f1 n f ( f1 ) aˆ f 2 n f ( f 2 ) n f1 1 n f1 n f ( f ) n f ( f1 ) n f ( f 2 )
f
f f1
1
f f1
1
2
f f1
1
f f1
1
2
aˆ f 2 aˆ f1 x f aˆ f 2 aˆ f1 n f ( f ) n f ( f ) aˆ f1 n f ( f1 ) aˆ f 2 n f ( f 2 ) n f1 1 n f1 n f ( f ) n f ( f1 ) n f ( f 2 )
f
Для f1 f 2 , [aˆ f1 , aˆ f 2 ] 0
[aˆ f1 , aˆ f 2 ] f1 , f 2
[aˆ f1 , aˆ f 2 ] [aˆ f1 , aˆ f 2 ] 0
фононы бозоны
2
2
8.
Число фононов не фиксировано (могут неограниченно рождаться)=>хим.потенциал фононного газа μ=0. В этом можно формально убедиться, вычислив
стат. сумму системы осцилляторов.
Hˆ
Hˆ
Z Sp exp n f exp n f
T n f
T
Hˆ
E n f
E n f
exp n f exp
n
Z
exp
f
T
T
T
nf
E n f E0 f n f
f
E0
f
2
f
энергия нулевый колебаний принимаем за начало отсчета энергии
f n f
E n f f n f Z exp
T
n f f
f
Осцилляторы независимые нет ограничений на совместное изменение чисел заполнения
Z
f n f
exp
T
f
n2 0
n1 0
n1 0
Z z f ; z f
f
f n
f
1 exp
exp
T
T
n 0
1
f
1 exp
T
zf
f
exp
2
T
n 0
f n
exp
T
9.
Кристаллическая решетка фононный газ : Z1
f
f
1 exp
T
Идеальный бозе газ со спектром одночастичных возбуждений f
и хим. потенциалом : Z
f
1
f
1 exp
T
В идеальном фононном газе хим. потенциал 0
nf
1
f
exp
T
E f n f
f
1
- среднее число фононов f
f
f
f
exp
T
- Равновесная теплоемкость кристаллической
1 решетки
10. Как определить собственные колебания?
Все элементарные ячейки одинаковые Атом можно указать с помощьювектора трансляции решетки n задает элементарную ячейку и номера j атома в элементарной ячейке
Положение равновесия атома : R n( 0, )j n ρ j
Мгновенное положение атома : R n , j (t ) R n( 0, )j u n , j (t )
U R ( 0 ) u
1
2
A
,
, 1
u u 1
, 1
,
2U
( 0 ), ( 0 ),
R R 1
силовые коэффициенты (характеризуют действующие на
атомы силы, которые возникают при их отклонении от
0
положения равновесия
Колебательное движение может иметь место только в том случае, когда
потенциальная энергия имеет вид потенциальной ямы. Положение равновесия
системы есть минимум ее потенциальной энергии.
,
A , 1
A , , 0 U
1
2
A
,
, 1
u u 1 положительно определенная квадратичная форма
, 1
,
можно перейти к нормальным координатам
11.
Нигде точках не происходит скачка силы (нет физических причин => U и еепервые производные – непрерывные => вторые производные U не зависят от
порядка дифференцирования
A , , 1 A 1 ,,
В основном объеме все элементарные ячейки - физически эквивалентны. =>
Энергия взаимодействия между атомами может зависеть только от положения их
в ячейке и от относительного положения ячеек, в которых они находятся, но не от
положений ячеек по отдельности.
A , , 1 A j ,,j 1 (n n1 )
Кристалл – периодическая структура => при параллельном переносе или при
повороте решетки как целого не возникает действующих на атомы
дополнительных сил
n1 , j1
A j ,,j 1 (n n1 ) 0
12.
Находим уравнения движенияH
p 2 1
2m j 2
u
p
1
1
1
1
2m j1
1
, 1
,
p
p
H
u p
A , , 1 u u 1
p H
u
2
1
1
2m j1 2 ,
1
,
2
p 21
2m j1 p
,
A 1 , 2 u 1 u 2
p
( p 1 p 1 )
p
1
p
1
2 p 1 1
2m j1
p
1
2m j1
1
1
1
p 21
2m j1
p 1 p 1
1
2m j1
p 1
p
1
p 1 p 1
p
p
p
1 ,
p 1 1 ,
m j1
mj
13.
pu
2m
p
2
1
1
1
2 ,
j1
1
,
2
1
A 1 ,, 2 u 1 u 2
2 u
,
A
u
1 , 2 1 u 2
1 , 2
,
(
u
u
)
u
u
1
1
,
1
2
2
1
A 1 ,, 2
A
u
u
1 , 2 1
2
2 ,
u
2 ,
u
u
1 2
1 2
,
,
1
A 1 ,, 2 u 1 , 2 , u 2 , 1 ,
2 ,
1
,
2
1
A 1 ,, 2 u 1 , 2 ,
A 1 ,, 2 u 2 , 1 ,
2 ,
1 , 2
1 2
,
,
1
A 1 ,, u 1
2 ,
1
A 1 ,, A , , 1
2 ,
A
,
1 ,
A , 2 u 2
,
u 1
1 ,
1
p
A , , 1 u 1
2 ,
1
A
,
, 1
u 1
1 ,
1 ,
A , 1 u 1
n1 , j1
,
A
,
j , j1
(n n1 )un 1 , j1
14.
p n , j m j u n , j pn1 , j1
m j u n , j
n1 , j1
A j , ,j 1 (n n1 )un 1 , j1
A j , ,j 1 (n n1 )un 1 , j1
-система dgN однородных ОДУ 2-го порядка с постоянными коэффициентами
=> общее решение – линейная комбинация гармонических решений (плоских
волн). Число плоских волн (фундаментальных решений) = число уравнений =
dgN.
Произвольное колебание кристаллической решетки
u n , j (t )
q ,
0
0
Q(q, ) u n , j (q, , t ) Q (q, ) u n , j (q, , t )
u n , j (q, , t ) ξ j (q, ) exp iqn i (q, )t - Собственное колебание
q - квазиволновой вектор (определяет направление распространения волны)
0
-номер ветви (нумерует собственные колебания с одинаковым q).
15.
Находим частоты и амплитуды собственных колебанийu n , j (q, , t ) ξ j (q, ) exp iqn i (q, )t m j u n , j
0
n1 , j1
m j i (q, s ) ξ j (q, s ) exp iqn i (q, s )t
2
n1 , j1
m j (q, s )ξ j (q, s )
j1 ,
n1
A j , ,j 1 (n n1 )ξ j1 (q, s ) exp iqn 1 i (q, s )t
exp iqn i (q, s )t m j 2 (q, s )ξ j (q, s ) exp iqn
n1 , j1
2
A j , ,j 1 (n n1 )un 1 , j1
A j , j1 (n n1 )ξ j1 (q, s ) exp iqn 1 0
,
A j , j1 (n n1 ) exp iq(n n1 ) ξ j1 (q, s ) 0
,
Замена n 2 n n
m j 2 (q, s ) m j ξ j (q, s )
j1 ,
(q, s ) m j ξ j (q, s )
2
j1 ,
n2
1
m j m j1
m j ξ j (q, s )
1
1
A j , ,j 1 (n 2 ) exp iqn 2
0
m
j1
n2
A j , j1 (n 2 ) exp iqn 2 m j1 ξ j1 (q, s ) 0
,
16.
2(q, s ) , j , j1 C j , ,j 1 (q) j1 (q, s ) 0 (*)
j1 ,
j (q, s ) m j ξ j (q, s )
1
C j , j1 (q)
m j m j1
,
A j ,,j 1 (n) exp iqn
n
Уравнение спектра
(*) ОСЛАУ det (q, s ) j , j1 C j , j1 (q) 0 собственных
колебаний
Алгебраическое уравнение порядка dg => каждому значению q соответствует dg
собственных колебаний.
2
,
,
Груперуем собственные колебания по порядку возростания частоты
(q,1) (q,2) (q,3g )
Совокупность всех собственных колебаний с данным s – s-я ветвь собственных
колебаний. Всего ветвей dg
17.
C j , ,j 1 (q) j1 (q, s ) 2 (q, s ) j (q, s ) уравнение на собственные значенияj1 ,
матрицы С (q) C j , ,j 1 (q)
,
j , j1
2 (q, s ) s ое cообственне значение матрицы С (q)
j (q, s )
j1
s ый собственный вектор матрицы С (q)
Проверим матрицу на эрмитовость
1
C j , j1 (q)
m j m j1
,
,
n
1
A j , j1 (n) exp iqn C j , j1 (q)
m j m j1
,
A j , j1 (n) A j , j1 (n) C j ,, j1 (q)
,
Замена n n C j ,, j1 (q)
1
m j m j1
1
m j m j1
,
A
,
j , j1
(n) exp iqn
n
A j , ,j 1 (n) exp iqn
n
A j , ,j 1 ( n) exp iqn
n
Отсутсвие скачков силы A j , ,j 1 (n n1 ) A j1 ,, j (n1 n) A j ,,j 1 ( n) A j1 ,, j (n)
C j ,, j1 (q)
1
m j m j1
A j1 ,, j (n) exp iqn
n
C j ,, j1 (q) C j1 ,, j (q) матрица C (q) эрмитовая
18.
Силовая матрица С(q) – эрмитовая.Собсвтвенные значения эрмитовой матрицы - вещественные
2 (q, s) - вещественные (можно показать, что сами частоты неорицательны)
Из линейно независимых собственных векторов эрмитовой матрицы можно
сформировать полную ортонормированную систему => амплитуды собственных
колебаний с данным волновым вектором образуют ПОНС
j (q, s) j (q, s1 ) s , s1
- условие ортогональности
j ,
j1 (q, s)
j (q, s1 )
s
j (q, s) j (q, s1 )
j ,
s
j ,
s
j1 (q, s) s , s1
s
j (q, s) j (q, s) j1 (q, s1 )
j (q, s) j (q, s) , j , j1
- условие полноты
19.
1C j , j1 (q)
m j m j1
,
A j , ,j 1 (n) exp iqn
n
Комплексно сопрягаем С и меняем q q
1
C j , j1 ( q)
m j m j1
,
A j , j1 (n) exp iqn C j ,, j1 ( q) C j1 ,, j (q)
,
n
2
(q, s ) , j , j1 C j , ,j 1 (q) j1 (q, s ) 0
2
( q, s ) , j , j1 C j ,,j 1 ( q) j1 ( q, s ) 0
j1 ,
j1 ,
Комплексно сопрягаем
2
( q, s )
,
j , j C j , j (q) j ( q, s) 0
,
1
1
1
j1 ,
( q, s) (q, s); j ( q, s ) j (q, s)
20.
1C j , j1 (q)
m j m j1
,
A j , ,j 1 (n) exp iqn
n
G вектор обратной решетки exp iGn 1
(q G , s ) (q, s )
C j , ,j 1 (q G ) C j , ,j 1 (q)
q G и q- физически
j (q G , s ) j (q, s )
эквивалентны
Волновой вектор имеет смысл рассматривать только в одной зоне Бриллюэна
(q, s ) - Непрерывная функция в первой зоне Бриллюэна => ограниченная
min (q, s ) max
21.
Проблема: Кристалл имеет конечные рамеры => нужны граничные условия. У насграничные условия призваны отражать физическую картину на границе
кристалла, как правило очень сложную.
Решение: Силы быстро убывают с расстоянием => в глубине кристалла граница
не ощущается => в объемных кристаллах можно срезать приграничную область, и
рассматривать только внутренний объем, в котором влиянием границы можно
пренебречь.
Внутренний объем разбиваем на одинаковые макроскопические
параллелепипеды, построенные на векторах элементарных трансляций.
Кристалл – периодическая структура => Все параллелепипеды – физически
эквивалентны => разумно потребовать, чтобы
0
0
u (r ) u (r L); L L e ; L N a
Физическая эквивалентность параллелепипеда (в среднем все одинаково) =>
достаточно рассмотреть только один параллелепипед с граничными условиями
0
0
u (0, x2 , x3 ) u ( L1 , x2 , x3 )
0
0
2
u
(
x
,
0
,
x
)
u
(
x
,
L
,
x
)
q
m , m 0, 1, 2, ; 1,2,3
1
3
1
2
3
N a
0
0
u ( x1 , x2 ,0) u ( x1 , x2 , L3 )
22.
Физически различные значения квазиволнового вектора лежат в пределах зоныБриллюэна.
Сколько физически различных значений квазиволнового вектора?
Выбор зоны Бриллюэна – вопрос удобства. Возьмем в качестве зоны Бриллюэна
параллелепипед, построенный на векторах элементарных трансляций обратной
решетки
2
q a q
m
L
2 a
L
L
m
m
L
2a
2a
N
N
L N a
m
2
2
Число физически различных значений квазиволнового вектора=число
элементарных ячеек.
Число различных собственных колебаний – утроенное число атомов
23.
2q
m
L
Спектр - квазидискретный
L макроскоп .
q ,i 1
dq f (q )
i
dq f (q )
k
dq f (q ); q ,i
q ,i
q ,i 1
f (q ,i )
i
V
f (k )
dkf (k )
3
2
q ,i
dq
i
2
2
m ,i q
(m ,i 1) k ,i 1
L
L
f (q ,i )
2
L
q
f (q )
L
2
dq
f (q )
24.
Анализ поведения ветвей при длинных волнах (в окрестности центра зоныБриллюэна qa<<1)
m j 2 (q, s )ξ j (q, s )
j1 ,
n1
A j , ,j 1 (n1 ) exp iqn 1 ξ j1 (q, s )
A j , ,j 1 (n1 ) 0
n1 , j1
Рассмотрим центр зоны Бриллюэна q 0
m j (0, s )ξ j (0, s )
2
j1 ,
m (0, s)ξ
2
j
j
(0, s )
j
(0, s )
2
m ξ
j
j
A j ,,j 1 (n1 ) A j1 ,, j
ξ j1 (0, s )
j
j1 ,
j
n1
ξ j1 (0, s )
A j , j1 (n1 )
,
n1
,
ξ j1 (0, s )
A j , j1 (n1 )
n1 , j
( n ) A
A j , j1 (n1 )
,
(n ) A ( n ) 0
(0, s ) 0;
m ξ (0, s ) 0
(0, s ) 0
(0, s ) 0; m ξ (0, s ) 0
(0, s )
j1 ,
,
1
j , j1
,
1
n1 , j
j1 , j
1
n1 , j
2
2 (0, s )
j
j
m j ξ j
j
j
2
j
j
j
25.
Ветви с ω(0)=0m j ξ j (0, s ) 0; 1, d число ветвей d
ξ j1 (0, s )
j
j1 ,
n1
A j , j1 (n1 ) 0 ξ j1 (0, s ) ξ (0, s )
,
(q; s )
1 2 s2
(q 0; s) (q 0; s)
q
q q 0
2 q q
,
2
(q; s )
( q; s ) (q; s ) q 0 минимум
0
q q 0
2 2
s
1
2 (q 0; s)
2 q q
,
q 0
q q 2
q
q q
q q
q 0
26.
Всегда существует d ветвей с звуковым характером закона дисперсии(акустические ветви)
s (q 0) cs (n q )q
q
cs
q
,
1 2 s2
2 q q
q 0
q q
q q
- скорость звука
в колебаниях акустических ветвей при длинных волнах все атомы в
элементарной ячейке смещаются практически одинаково, т.е. элементарная
ячейка колеблется как целое. Длинные волны – накрывают много ячеек =>
замыватся дискретность среды => получаются эффективно волны в сплошной
среде - звук
27.
Если число атомов в элементарной ячейке g>1, то существует d(g-1) оптическихветвей c
s (q 0) s ,0 0
s (q 0) s ,0 1
j
1
2
s ,0
,
1 2 s2
2 q q
n n q 2
q 0
m j ξ j (0, s ) 0 в колебаниях оптических ветвей при длинных волнах
положение центра тяжести элементарной ячейки
практически не меняется, т.е. ячейка деформируется
28.
un , j (t )Q(q, s)
j (q, s )
mj
q,s
Q (q, s )
mj
exp iqn i (q, s )t
1
mj
mj
Q ( q , s )
Q (q, s)
q,s
mj
exp iqn i ( q, s )t
mj
j (q, s )
exp iqn i (q, s )t
j ( q, s )
q,s
j ( q, s ) j (q, s )
( q, s ) ( q, s )
un , j (t )
Q (q, s)
j (q, s )
q,s
j (q, s )
q,s
exp iqn i (q, s )t
exp iqn i (q, s )t
Q ( q , s )
j (q, s )
q,s
mj
exp iqn i (q, s )t
(q, s) exp iqn Q(q, s) exp i (q, s)t Q (q, s) exp i (q, s)t
j
q,s
f (q, s ); f ( q, s )
un , j (t )
1
Nm j
~
~
f , j exp iqn Q f (t ) Q * f (t )
f
~
Q f (t ) N Q f exp i f t - обобщенные координаты (указав их, задаю мгновенное
положение решетки). Меняются по гармоническому закону =>
нормальные координаты
un , j (t )
1
Nm j
f
~
~
f , j exp iqn Q f (t ) Q * f (t ) H
n , j ,
m j u n , j u n , j
2
1
2
n ,n1
j , j1
,
A j , ,j 1 (n n1 )un , j un 1 , j1
29.
H 2 2f Q *f Q ff
Перейдем к вещественным нормальным координатам
2
2
1 2
2
p
x ip / x ip /
2 2
2
x 2 2 2
H p x
2
4
2
2
pf
1
Qf
xf
2
i f
*
x
Q
Q
f
f
f
*
p
i
Q
Q
p
1
f
f
f
f
f
Q *f x f
2
i f
H Hf ; Hf
f
p 2f
2
2f x 2f
2
30.
E(q, ) n q, E
q ,
V
2 3
зона
Бриллюэна
dq
(q, )
(q, )
exp
1
T
Низкие температуры – основной вклад дают звуковые колебания акустических
ветвей (звуковые акустические фононы)
В знаменателе подынтегрального выражения стоит экспонента => основной вклад
в ET дают колебания с частотой (q; )
При каких температурах этому условию удовлетворяют только звуковые
колебания акустических ветвей?
сзв /
c
cзв / a зв
a
a
- При этих температурах можно учитывать
только вклад звуковых колебаний
акустических ветвей
q
(q, ) cзв q
q
2
q 1
q - усредняем скорость звука
1
cзв
d
d
sin
c
зв
q 3 4 0 0
q
31.
EV
2 3
зона
Бриллюэна
dq
(q, )
(q, )
exp
1
T
Под знаком интеграла стоит экспонена=> в подынтегральной функции можно
брать закон дисперсии акустических ветвей и распространять интегрирование на
все q-пространство (основной вклад дают звуковые колебания => ошибка мала)
E
V
2 3
dq
с q
V
4
3
с q
2
exp 1
T
Обезразмеривающая замена переменной z
V 4
E
2 3 3
1
с
0
dqq 2
c s q
z3
dz
4
exp( z ) 1
E
2V
СV T T 3 ; k B 2 3
T
1
с
0
z3
dz
exp( z ) 1
с q
с q
exp 1
T
32.
Высокие температуры – возбуждены все собственные колебанияq,
1
T
x
T
q , exp x 1
max q, (q, ) x
- Малый параметр.
Нужно проводить
разложение в ряд
Тейлора
q,
E
q,
q ,
exp
1
T
x
x
1
2
3
2
x
x
x x
exp x 1
1 x o x 3 1 1 o x 2
2 6
2 6
x x2 x2
x x2
1
1
2 6
4
2 12
q,
q, 2
2
q,
ET
T 1
2
12 q ,
q,
q ,
q ,
q ,
exp
1
T
33.
q,q, 2
E
T 1
2
12T
q,
q ,
q ,
q ,
exp
1
T
q,
2
q,
1 dgN - Полное число собственных колебаний
q,
q,
- энергия нулевых колебаний
E0
2
q ,
2
1
dgN
2 q,
q ,
2
12T
2 q,
q ,
2 2
12
2 2 1
ET E0 dgN T
12
T
2
2
ET
1
CV k B
k B dgN 1
2
T
12
T
При T
2 , CV k B dgN - Закон Дюлонга-Пти
1
T
34.
Нужно вычислять f ( f )f
Нужно перейти от суммирования по квантовым числам к интегрир. по энергии
d f ( ) f (
f
f
)
f
f ( f ) d f ( ) f d f f ( )
f
f
d g f ( ), g f
f
0
1, 0 f 0
d g f d f 0, иначе
0
0
d g
0
-число собственных колебаний с частотой в интервале
1
0 0
ω0- ω 0+Δ ω
g - плотность собственных колебаний
dN g d - Число собственных колебаний с частотой в физ. беск. малом интерв
35.
f (f
) d g ( ) f ( ),
f
g f
f
F
f
V
dq (q; s )
3
2 s зоне Б .
f
ln 1 exp
T
d g ( ) ln 1 exp
T
Через плотность собственных колебаний можно выразить любую
макроскопическую характеристику. Наличие особенностей в плотности
колебаний отражается на измеряемых величинах
36.
Оператор смещения атомов1
Nm j
un , j
f , j exp iqn Q f
f
pf *
1
; Q f
Qf xf
2
i f
Квантовая механика
1
Nm j
uˆn , j
pf
1
xf
2
i f
f , j exp iqn Qˆ f
f
pˆ f
1
Qˆ f xˆ f
2
i f
1
Nm j
f,j
exp iqn Q *f
f
1
Nm j
f , j exp iqn Qˆ f
f
x2
x
xˆ n
exp
xH
n
2
n
2
2 n!
1
x 2 1
x
x
1
xHn ( x) H n 1 ( x) nH n 1 ( x) xˆ n
exp
H
nH
n
1
n
1
2
n
2
2
2
2 n!
x2
exp
2
n 1
2
2
(
n
1
)!
2 n 1 (n 1)!
x
1
H n 1 n
n
n 1
2
2 n!
2 (n 1)!
2 n n!
1
1
n 1 n 1
n n 1
aˆ n aˆ n
2
2
2
xˆ
2
aˆ
aˆ
x
H n 1
n 1
2 (n 1)!
x2
exp
2
2
37.
pˆ n in
x
1
x2 x
H
n
exp
2 n
n
2
2 n!
x2 x
1
1
H
pˆ n i 2 x n
exp
2 n
n
2 n!
2
x 2 x 2n
x2
x
1
H n ( x) 2nH n ( x)
exp
H
exp
H
2 n
2 n 1
n
n
2 2 n!
2
2 n!
1
2n 2 n 1 (n 1)!
2 n n!
xˆ
pˆ
2
aˆ aˆ pˆ
i
aˆ aˆ
2
n
x2
2
2
x
exp
H
n
aˆ n
n 1
2 n 1
n 1
2
2
2
2 (n 1)!
1
i
aˆ aˆ 2aˆ n
2
38.
xˆ f2
aˆ
aˆ f
f
i
aˆ f aˆ f
2
pˆ f
pˆ f
1
ˆ
Qf
xˆ f
2
i f
pˆ f
1
ˆ
2
1 Qf
xˆ f
f
f
2
i f
Qˆ f
1
Nm j
uˆn , j
uˆn , j
aˆ f ; Qˆ f
2 f
f
f
2 f
aˆ f
2 f
aˆ f
f , j exp iqn Qˆ f
aˆ f aˆ f aˆ f aˆ f
2
2 2
f
1
Nm j
f , j exp iqn aˆ f
2 Nm j f
f
f , j exp iqn Qˆ f
f
f , j exp iqn aˆ f
2 Nm j f




































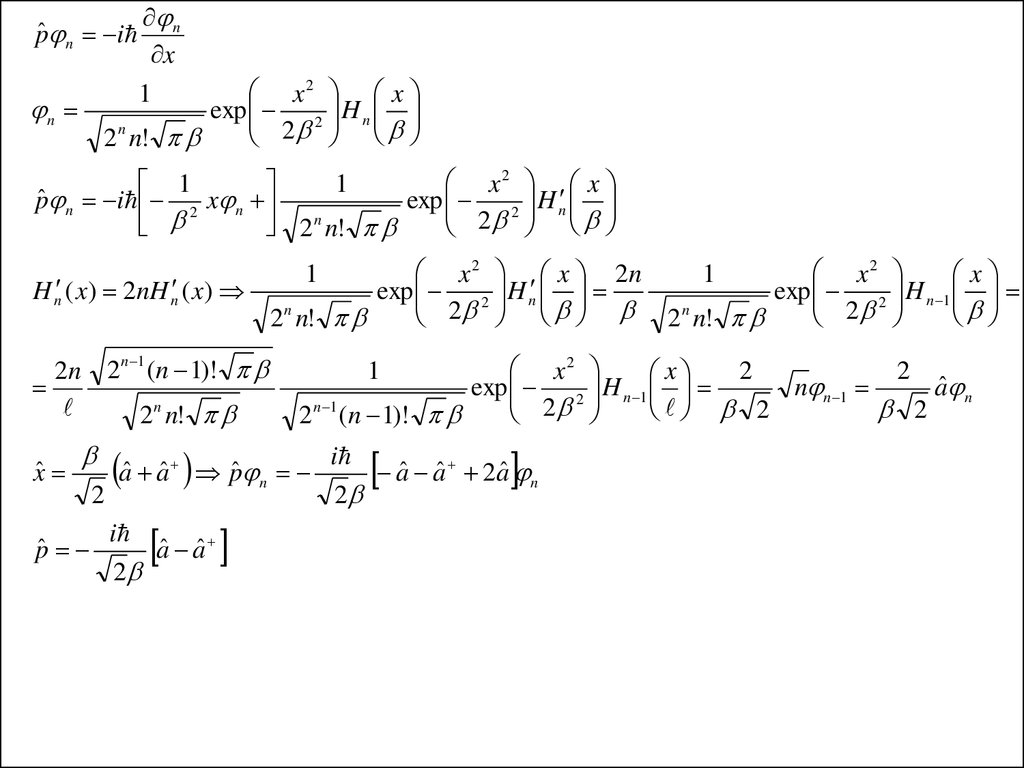
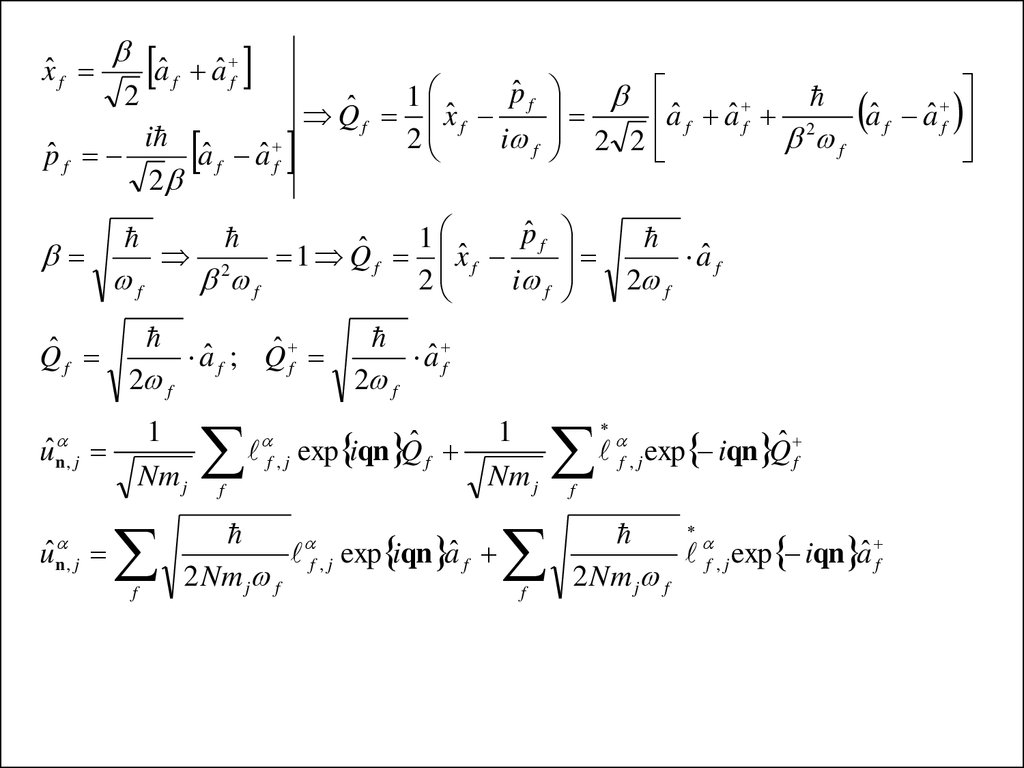
 Физика
Физика








