Динамика кулисного механизма

1. Динамика кулисного механизма

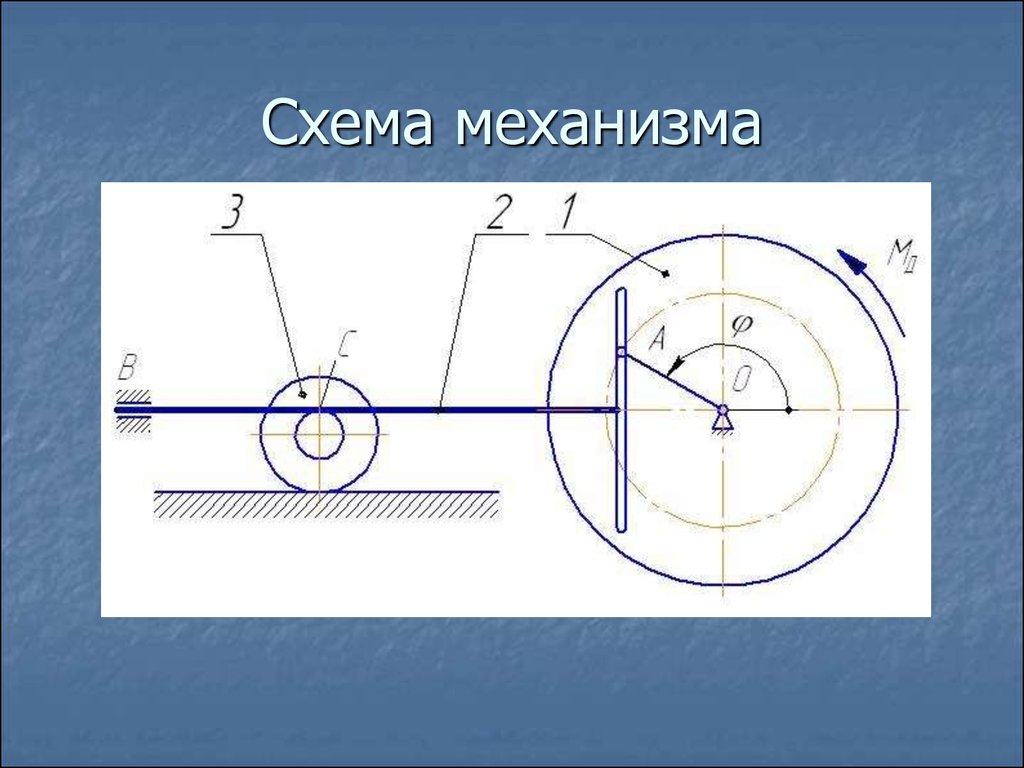
Вариант 23110713

2. Схема механизма

3. Кинематический анализ механизма

Определены кинематические характеристики:
скорость т.А
скорость кулисы
ускорение кулисы
скорость центра катка
ускорение центра катка
угловая скорость катка
угловое ускорение катка

4.

Записаны уравнения геометрических связей:
xA = OA · cos φ;
yA = OA · sin φ;
xC2 = xC20 + OA · cos φ;
yC2 = 0;
xC3 = xC30 – (R3/(r3+R3)) · OA · cos φ; yC3 = -r3;
φ3 = -(OA · cos φ)/(r3+R3).

5. Угловая скорость и угловое ускорение маховика

Получены выражения для:
кинетической энергии системы
2
I1 2 m2
·OA · sin 2 m3 R3 · ·OA ·sin I 3 1 · · OA ·sin
T
2
2
2 r3 R3
2 r3 R3
приведенного момента инерции механизма и его
производной по углу поворота маховика
2
R3 3
m1 R1
· OA · sin 2
I пр
m2 m3
2
r3 R3
2
dI пр
R3 3
· OA 2 ·sin 2
m2 m3
d
r3 R3
2
Найдены значения Iпр= 5,67 кг·м2; dIпр/dφ= -1.688 кг·м2
для заданного положения механизма.
2

6.

получено дифференциальное уравнение движения
механизма для заданных числовых значений
5,184 1,949 ·sin · 0,975·sin 2 ·
2
2
34
определена угловая скорость маховика ω1 = 5,60
рад/с и его угловое ускорение ε1=10,66 рад/с2.

7. Реакции связей и уравновешивающая сила

определены реакции опоры маховика в
заданном положении механизма
XO=177,2 Н; YO=0
определена сила взаимодействия маховика и
кулисы
NA=177,2 Н
определена горизонтальная проекция
уравновешивающей силы, которую нужно
приложить к оси катка для равновесия
механизма
Fx=401,4 Н

8. Дифференциальное уравнение движения кулисного механизма

С помощью уравнения Лагранжа второго рода
и уравнения движения машины получены два
одинаковых дифференциальных уравнения
движения данного механизма, которые
совпали с приведенным выше, а именно:
5,184 1,949 ·sin · 0,975·sin 2 ·
2
2
34