Плоская система сил

1.

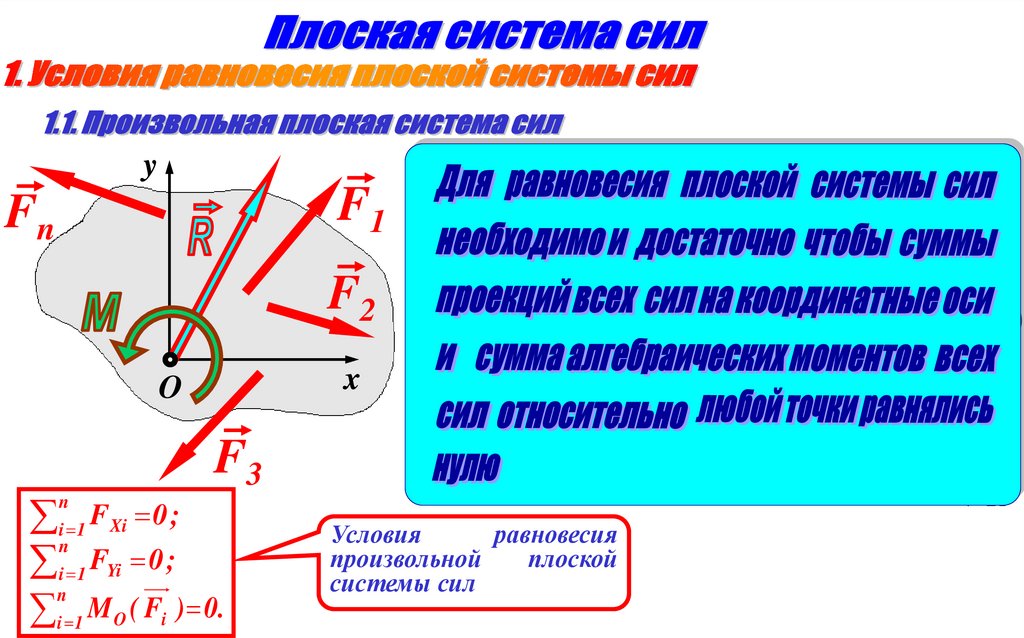
y
F1
Fn
F2
x
O
F3
i 1 FXi 0 ;
n
i 1 FYi 0 ;
n
i 1 M O ( Fi ) 0.
F , F , F ,..., F ; F , F , F ,..., F R , M
1
2
3
n
1
2
3
Главный вектор находится в плоскости
системы и определяется как векторная
сумма сил, входящих в систему:
Главный момент перпендикулярен
плоскости системы. Модуль – сумма
алгебраических
моментов
сил,
входящих в систему относительно
центра приведения:
RX
RY
n
F ;
i 1 Xi
n
F ;
i 1 Yi
R
n
Условия
равновесия
произвольной
плоской
системы сил
2
RX
2
RY
;
n
R
MO
n
i 1
Fi
n
M (F
i 1 O i
cos( x , R )
Rx
cos( y , R )
Ry
R
R
)
,
.

2.

y
F1
Fn
F2
O
F3
0 i 01 ;FXi 0 ;
n
i 1 FYi 0 ;
n
i 1 M O ( Fi ) 0.
n
x
i 1 FYi 0 ;
n
i 1 M O ( Fi ) 0.
n
Условия равновесия
плоской
системы
параллельных сил

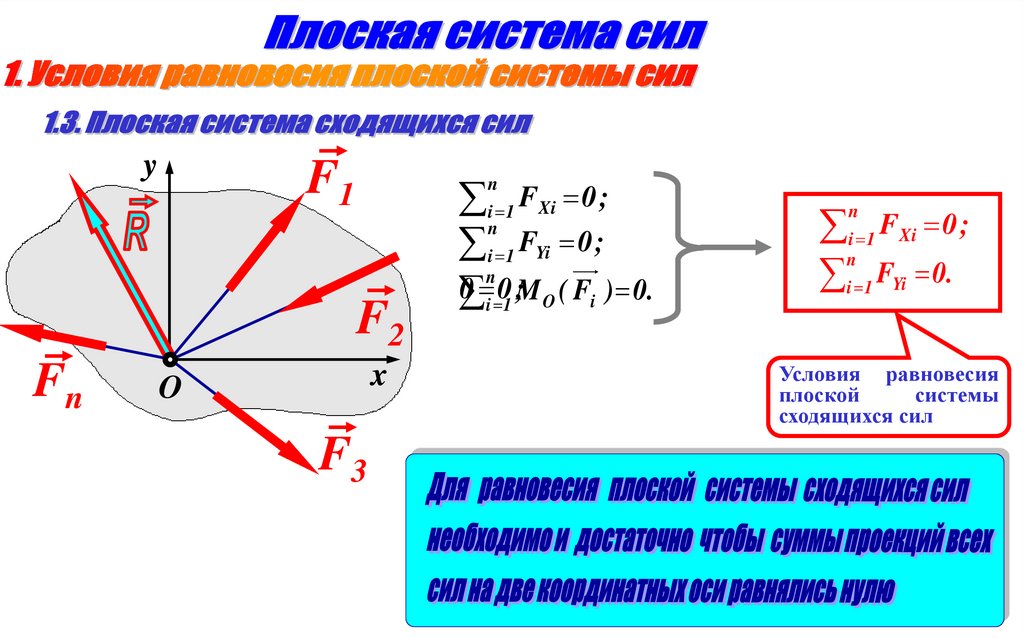
3.

y
F1
F2
Fn
i 1 FXi 0 ;
n
i 1 FYi 0 ;
n
0 i 01 ;M O ( Fi ) 0.
n
x
O
F3
i 1 FXi 0 ;
n
i 1 FYi 0.
n
Условия равновесия
плоской
системы
сходящихся сил

4.

F , F , F ,..., F R , M
y
1
F1
Fn
x
3
n
O
R i 1 Fi 0 ;
n
M O i 1 M O ( Fi ) 0 ;
MO
d
;
R
,
M
R
,
R
,
R
,
M
;
O
1
2
O
2
R
Пара сил R2 , R имеет алгебраический момент
M1 d R MO
M1 MO 0 ;
n
F
O
2
R , M R , R , R
F3
O
1
2
, M O R1 .
O1
d M
R

5.

F , F , F ,..., F R , M
y
1
F1
Fn
F3
x
3
n
i 1 FXi 0 ;
n
i 1 FYi 0 ;
n
i 1 M O ( Fi ) 0.
n
F2
O
2
O

6.

F1
B
Fn
h
А
F3
i 1 FXi 0 ;
n
i 1 FYi 0 ;
n
i 1 M O ( Fi ) 0.
n
C
F , F , F ,..., F M
1
2
3
n
A ,MB
, MC
F2
Необходимость: Определяется третьим уравнением
1-й
n формы условий.
Достаточность: Для любой из точек, взятых за центр
A система
i
iприведения,
1
приводится к
nравнодействующей
R
M ( F ) 0;
( Fi ) 0 ;
i 1 M
B
M ( F ) M
n
i 1 M C (MFi( F) ) 0RM
На
основании
теоремы
Вариньона для точек А и В:
n
i 1
n
i 1
A
i
B
i
R) 0
B( R ) 0
A(
Это может быть только тогда, когда равнодействующая
проходит
через точки А и В.
Для точки С в качестве центра приведения выполняется равенство:
MС ( R ) h R 0 ; h 0
R 0 что достаточно.

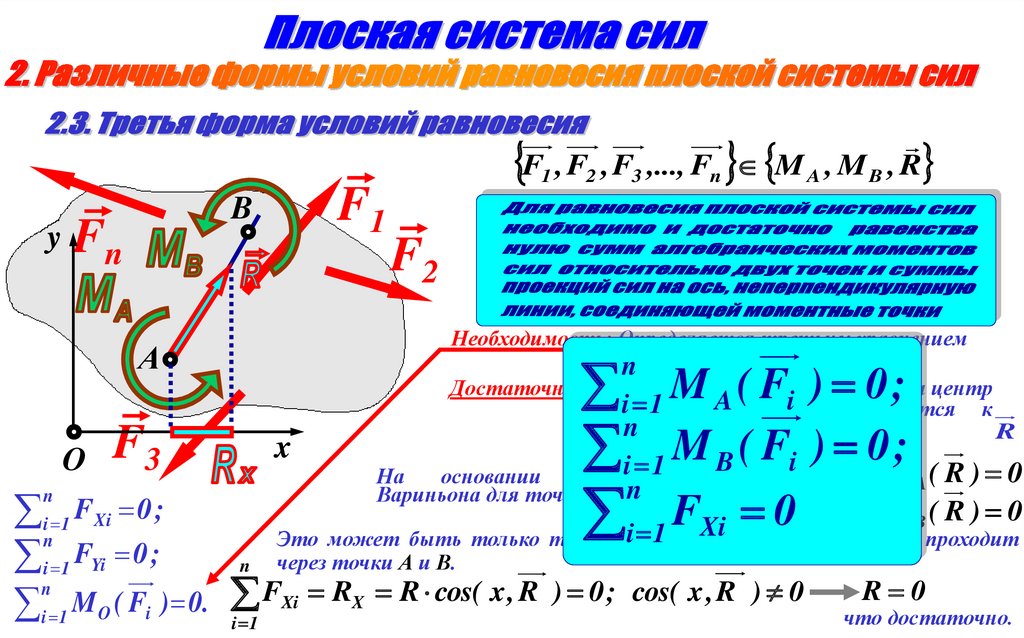
7.

F1 , F2 , F3 ,..., Fn M A , M B , R
y
F1
B
Fn
А
O
F3
x
F2
Необходимость: Определяется третьим уравнением
1-й
n формы условий.
Достаточность: Для любой из точек, взятых за центр
A система
i
iприведения,
1
приводится к
nравнодействующей
R
M ( F ) 0;
( Fi ) 0 ;
i 1 M
B
M ( F ) M
На
основании
теоремы
Вариньона для точек А и n
В:
n
A
i
i 1
n
M B ( Fi
i
1
Xi
R) 0
) MB( R ) 0
A(
i 1 FXi 0 ;
0
Это может быть только тогда, когда равнодействующая R проходит
n
i 1 FYi 0 ;
n через точки А и В.
n
R 0
FXi RX R cos( x , R ) 0 ; cos( x , R ) 0
M
(
F
)
0
.
i 1 O i
что достаточно.
i 1
n
F
i 1

8.

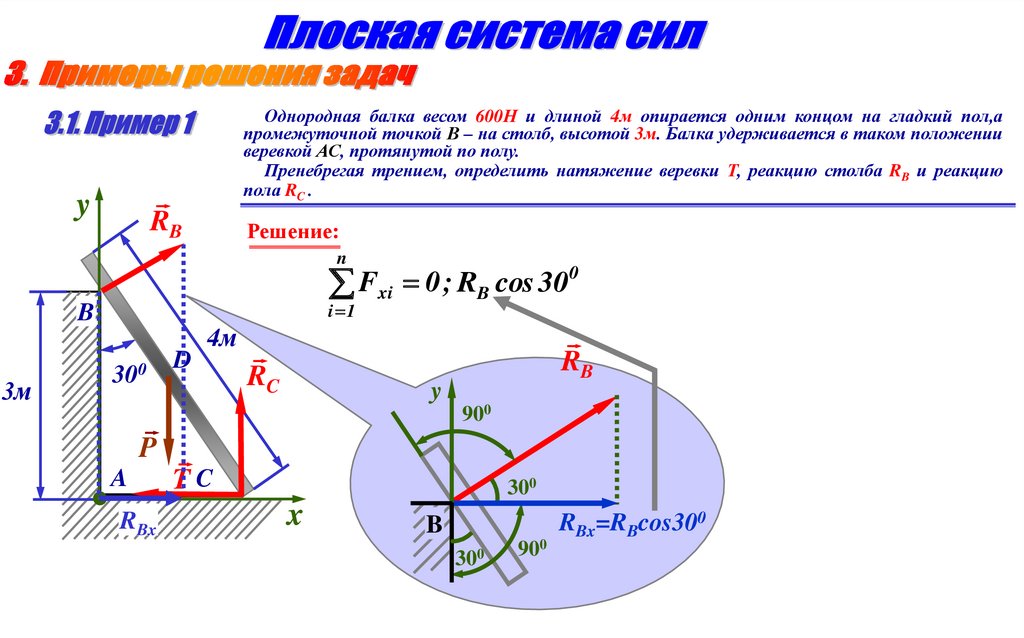
Однородная балка весом 600Н и длиной 4м опирается одним концом на гладкий пол,а
промежуточной точкой В – на столб, высотой 3м. Балка удерживается в таком положении
веревкой АС, протянутой по полу.
Пренебрегая трением, определить натяжение веревки Т, реакцию столба RB и реакцию
пола RC .
y
RB
Решение:
n
0
F
0
;
RB cos 30
xi
i 1
B
3м
300
D
4м
RC
RB
y
900
P
A
RBx
TC
300
x
B
300
900
RBx=RBcos300

9.

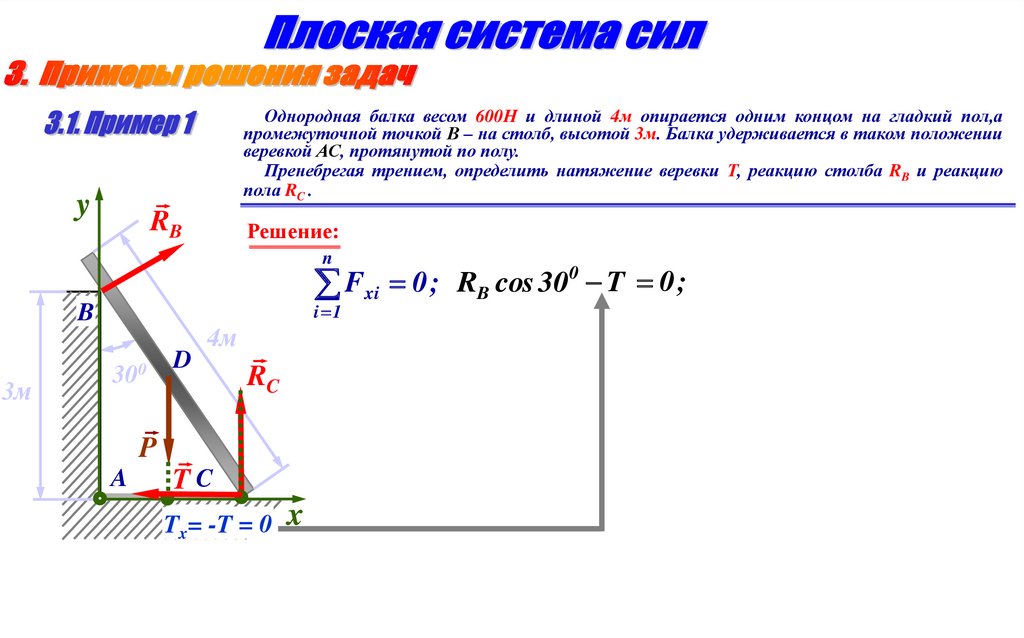
Однородная балка весом 600Н и длиной 4м опирается одним концом на гладкий пол,а
промежуточной точкой В – на столб, высотой 3м. Балка удерживается в таком положении
веревкой АС, протянутой по полу.
Пренебрегая трением, определить натяжение веревки Т, реакцию столба RB и реакцию
пола RC .
y
RB
Решение:
n
Fxi 0 ;
i 1
B
3м
300
D
4м
RC
P
A
TC
0Cx= 0
R-T
TPx=
x=
x
RB cos 30 T 0 ;
0

10.

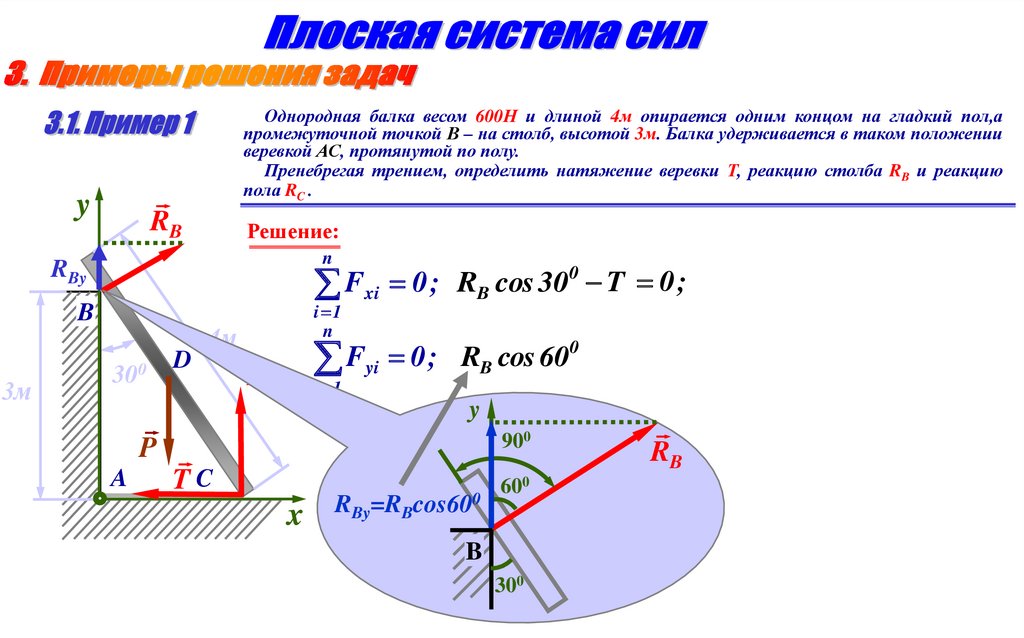
Однородная балка весом 600Н и длиной 4м опирается одним концом на гладкий пол,а
промежуточной точкой В – на столб, высотой 3м. Балка удерживается в таком положении
веревкой АС, протянутой по полу.
Пренебрегая трением, определить натяжение веревки Т, реакцию столба RB и реакцию
пола RC .
y
RB
Решение:
n
Fxi 0 ;
RBy
i 1
n
B
3м
300
D
4м
RB cos 30 T 0 ;
0
0
F
0
;
R
cos
60
yi
B
RC
i 1
y
900
P
A
TC
x
RBy=RBcos600
600
B
300
RB

11.

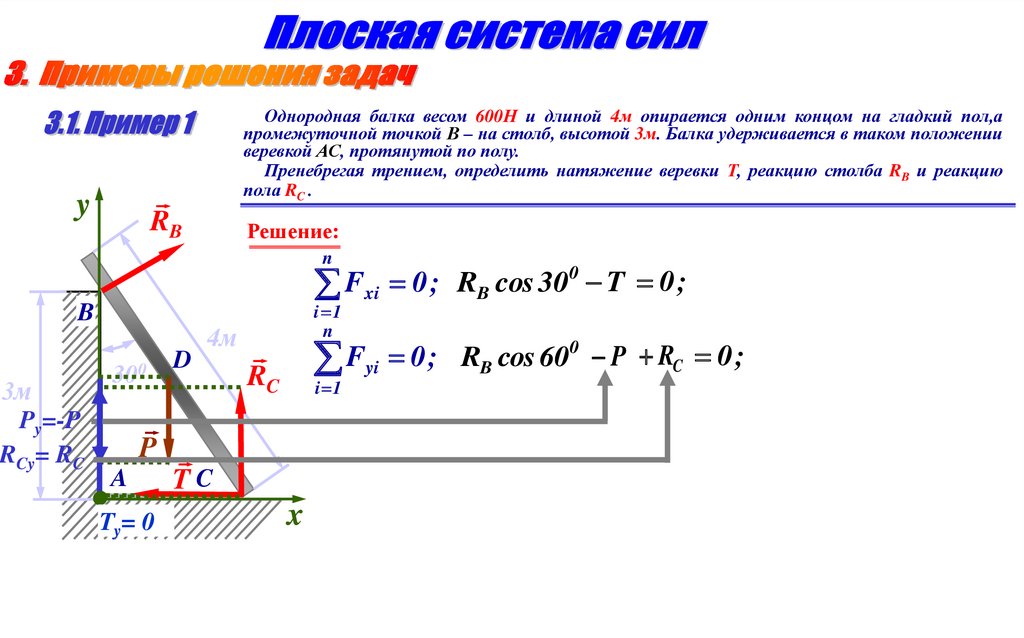
Однородная балка весом 600Н и длиной 4м опирается одним концом на гладкий пол,а
промежуточной точкой В – на столб, высотой 3м. Балка удерживается в таком положении
веревкой АС, протянутой по полу.
Пренебрегая трением, определить натяжение веревки Т, реакцию столба RB и реакцию
пола RC .
y
RB
Решение:
n
Fxi 0 ;
i 1
n
B
3м
Py=-P
RCy= RC
300
D
4м
0
P RC 0 ;
F
0
;
R
cos
60
yi
B
RC
i 1
P
A
Ty= 0
RB cos 30 T 0 ;
0
TC
x

12.

Однородная балка весом 600Н и длиной 4м опирается одним концом на гладкий пол,а
промежуточной точкой В – на столб, высотой 3м. Балка удерживается в таком положении
веревкой АС, протянутой по полу.
Пренебрегая трением, определить натяжение веревки Т, реакцию столба RB и реакцию
пола RC .
y
RB
Решение:
n
Fxi 0 ;
900
B
3м
h1
300
P
A
=BC=AB/cos300
4м
D
RC
i 1
n
RB cos 30 T 0 ;
0
0
P RC 0 ;
F
0
;
R
cos
60
yi
B
i 1
n
M C ( Fi ) 0 ; R
900
i 1
TC
x
h2=DC·sin300
Ответ:
3
B cos 30 0
P 2 sin 30 0 ;
0
R 2 P sin 30 cos 30 / 3 173.2 H ;
моментная точка – С0
B
0
RC P RB sin 30 0 513.4 H ;
T RB cos 30 150 H .
RB 173.2 H , RC 513.4 H , T 150 H .
0

13.

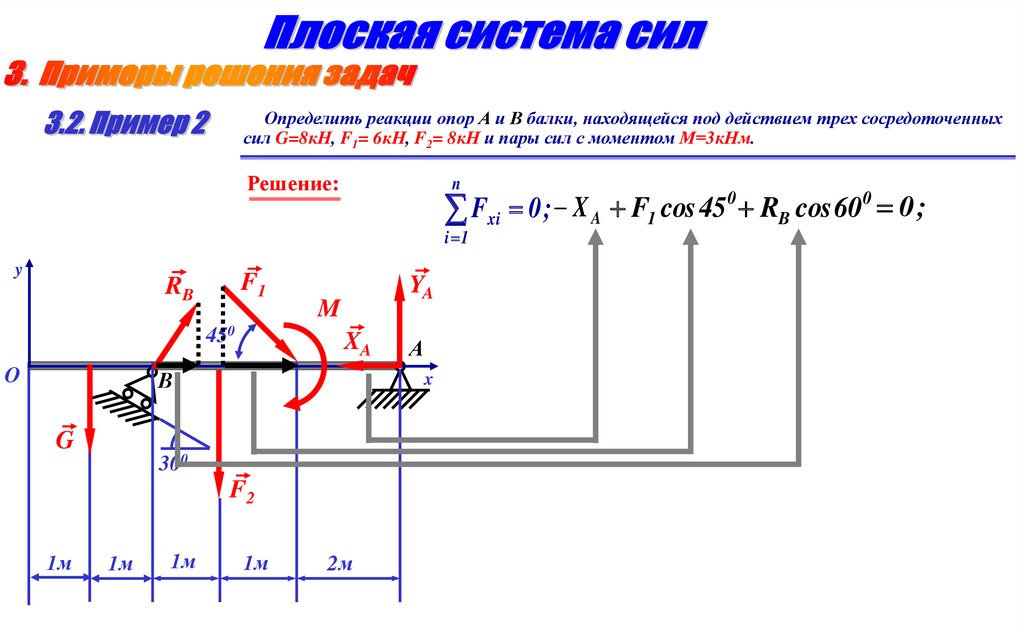
Определить реакции опор А и В балки, находящейся под действием трех сосредоточенных
сил G=8кН, F1= 6кН, F2= 8кН и пары сил с моментом М=3кНм.
Решение:
n
Fxi 0 ; X A F1 cos 45
i 1
y
F1
RB
450
O
YA
M
XA
В
x
G
300
F2
1м
1м
1м
А
1м
2м
0
RB cos 60 0 ;
0

14.

Определить реакции опор А и В балки, находящейся под действием трех сосредоточенных
сил G=8кН, F1= 6кН, F2= 8кН и пары сил с моментом М=3кНм.
Решение:
n
Fxi 0 ; X A F1 cos 45
i 1
n
y
F1
RB
450
O
M
i 1
XA
300
F2
1м
А
x
G
1м
1м
RB cos 60 0 ;
0
0
0
G 0;
F
R
sin
60
F
sin
45
F
0
;
YA
YA yi
2
B
1
В
1м
0
2м

15.

Определить реакции опор А и В балки, находящейся под действием трех сосредоточенных
сил G=8кН, F1= 6кН, F2= 8кН и пары сил с моментом М=3кНм.
Решение:
h=
y
F1
RB
450
O
n
M
XA
300
F2
1м
А
i 1
n
M A 0 ; 2 F1 sin 45 3F2 4 RB sin60 5G M
x
i 1
G
1м
i 1
n
1м
RB cos 60 0 ;
0
0
0
R
sin
60
F
sin
45
F
0
;
YA
F2 G 0 ;
YA yi
B
1
В
1м
Fxi 0 ; X A F1 cos 45
4 sin600
0
h= 2 sin450
2м
0
0
0;

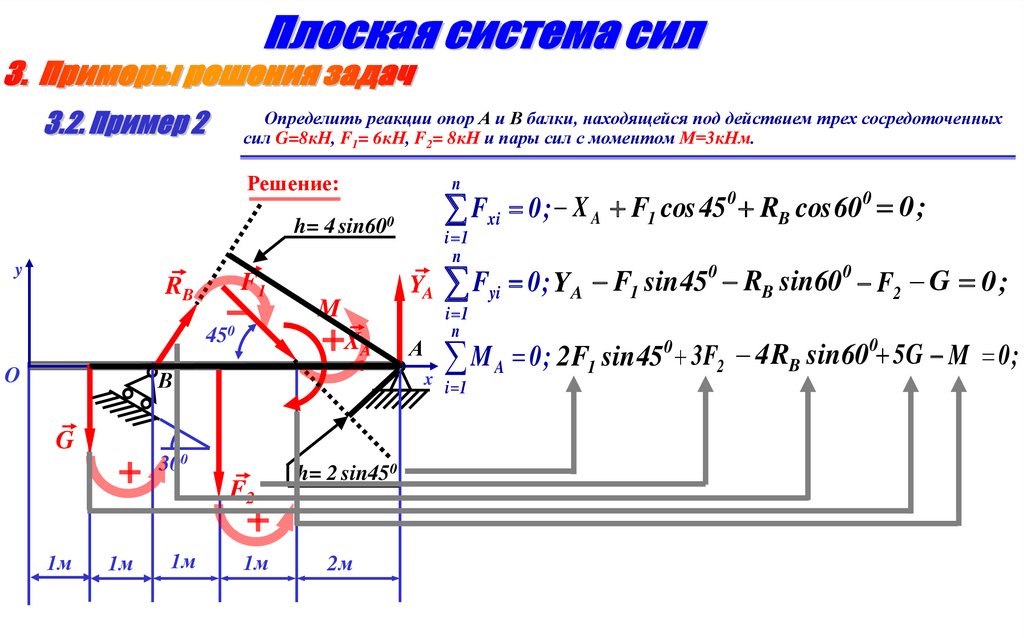
16.

Определить реакции опор А и В балки, находящейся под действием трех сосредоточенных
сил G=8кН, F1= 6кН, F2= 8кН и пары сил с моментом М=3кНм.
Решение:
n
Fxi 0 ; X A F1 cos 45
i 1
n
y
F1
RB
450
O
M
XA
M A 0 ; 2 F1 sin 45 3F2 4 RB sin60 5G M
x
0
0
0;
M F1 2 sin 45 0 F2 3 G 5
RB
20.06 кН ;
0
4 sin 60
YA F1 sin 450 RB sin600 F2 G 38.08 кН ;
300
F2
1м
А
i 1
n
i 1
G
1м
RB cos 60 0 ;
0
0
0
R
sin
60
F
sin
45
F
0
;
YA
F2 G 0 ;
YA yi
B
1
В
1м
0
1м
X A F1 cos 450 RB cos 600 14.27 кН .
2м
Ответ:
RB 20.06 кH , X A 14.27 кH , YA 38.08кH .
Знак «–» показывает, что реакция направлена в сторону,
противоположную показанной на расчетной схеме.

17.

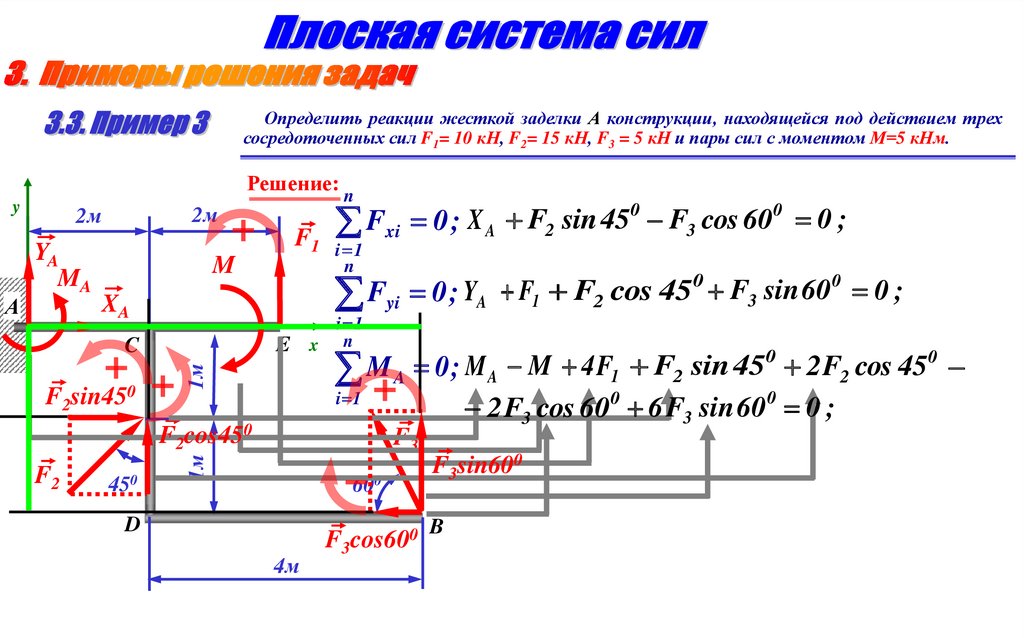
Определить реакции жесткой заделки А конструкции, находящейся под действием трех
сосредоточенных сил F1= 10 кН, F2= 15 кН, F3 = 5 кН и пары сил с моментом М=5 кНм.
Решение:
y
YA
MA
F1
M
0
0
0;
F
cos
60
F
sin
45
X
F
0
;
xi
3
2
A
i 1
XA
E x
1м
C
F2
450
F3
1м
А
2м
2м
n
600
B
D
4м

18.

Определить реакции жесткой заделки А конструкции, находящейся под действием трех
сосредоточенных сил F1= 10 кН, F2= 15 кН, F3 = 5 кН и пары сил с моментом М=5 кНм.
Решение:
y
YA
MA
F1
M
0
0
0;
F
cos
60
F
sin
45
X
F
0
;
xi
3
2
A
i 1
n
Fyi 0 ; YA
XA
i 1
E x
1м
C
F2
450
F3
1м
А
2м
2м
n
600
B
D
4м
F1 F2 cos 45 F3 sin 60 0 ;
0
0

19.

Определить реакции жесткой заделки А конструкции, находящейся под действием трех
сосредоточенных сил F1= 10 кН, F2= 15 кН, F3 = 5 кН и пары сил с моментом М=5 кНм.
Решение:
y
YA
MA
F1
M
E
F2sin450
1м
C
0
0
0;
F
cos
60
F
sin
45
X
F
0
;
xi
3
2
A
i 1
n
Fyi 0 ; YA
XA
i 1
x n
F2cos450
F2
450
F3
600
D
F3cos600
4м
F1 F2 cos 45 F3 sin 60 0 ;
0
M A 0 ; M A M 4 F1 F2 sin 45
0
2 F2 cos 45
0
0
2 F3 cos 60 6 F3 sin 60 0 ;
i 1
1м
А
2м
2м
n
F3sin600
B
0
0

20.

Определить реакции жесткой заделки А конструкции, находящейся под действием трех
сосредоточенных сил F1= 10 кН, F2= 15 кН, F3 = 5 кН и пары сил с моментом М=5 кНм.
Решение:
y
YA
MA
F1
M
E
1м
F2
450
i 1
n
Fyi 0 ; YA
XA
C
0
0
0;
F
cos
60
F
sin
45
X
F
0
;
xi
3
2
A
i 1
x n
F1 F2 cos 45 F3 sin 60 0 ;
0
M A 0 ; M A M 4 F1 F2 sin 45
i 1
F3
1м
А
2м
2м
n
600
B
D
4м
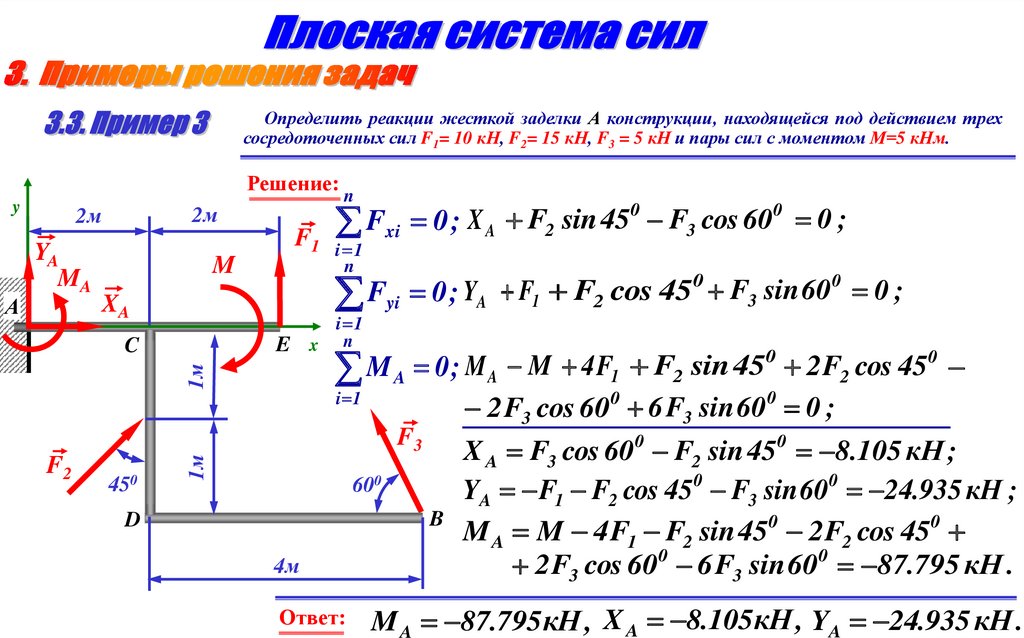
Ответ:
0
2 F2 cos 45
0
0
2 F3 cos 60 6 F3 sin 60 0 ;
0
0
X A F3 cos 60 F2 sin 45 8.105 кН ;
0
0
YA F1 F2 cos 45 F3 sin 60 24.935 кН ;
M A M 4 F1 F2 sin 450 2 F2 cos 450
2 F3 cos 600 6 F3 sin 600 87.795 кН .
0
0
M A 87.795кH , X A 8.105кH , YA 24.935 кH .