Трапеция

1. Трапеция

2.

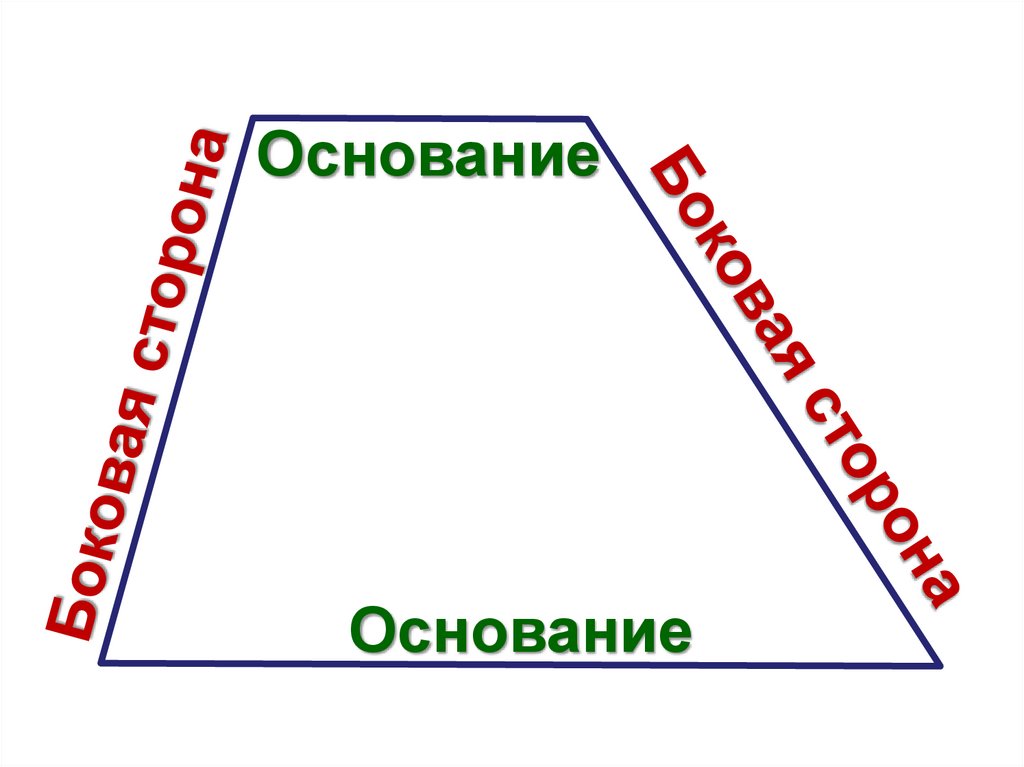
Трапецией называется
четырёхугольник, у
которого две стороны
параллельны, а две
другие стороны не
параллельны

3.

Основание
Основание

4.

Трапеция называется
равнобедренной, если её
боковые стороны равны

5.

Трапеция, один из углов
которой прямой,
называется прямоугольной

6.

Отрезок, соединяющий
середины боковых сторон
трапеции, называется
средней линией трапеции
B
C
M
A
N
D

7.

M – середина АВ,
N – середина CD
MN – средняя линия трапеции
B
M
A
C
N
D

8.

Свойство углов
равнобедренной трапеции
B
C
D
A
В равнобедренной трапеции
углы при каждом основании
равны

9.

B
A
C
D
Дано: ABCD –
равнобедренная трапеция
Доказать: A = D, B = C

10.

Доказательство:
B
C
A
D
E
1. Проведём СЕ АВ.
СЕ АВ и ВС АD
ABCЕ – параллелограмм

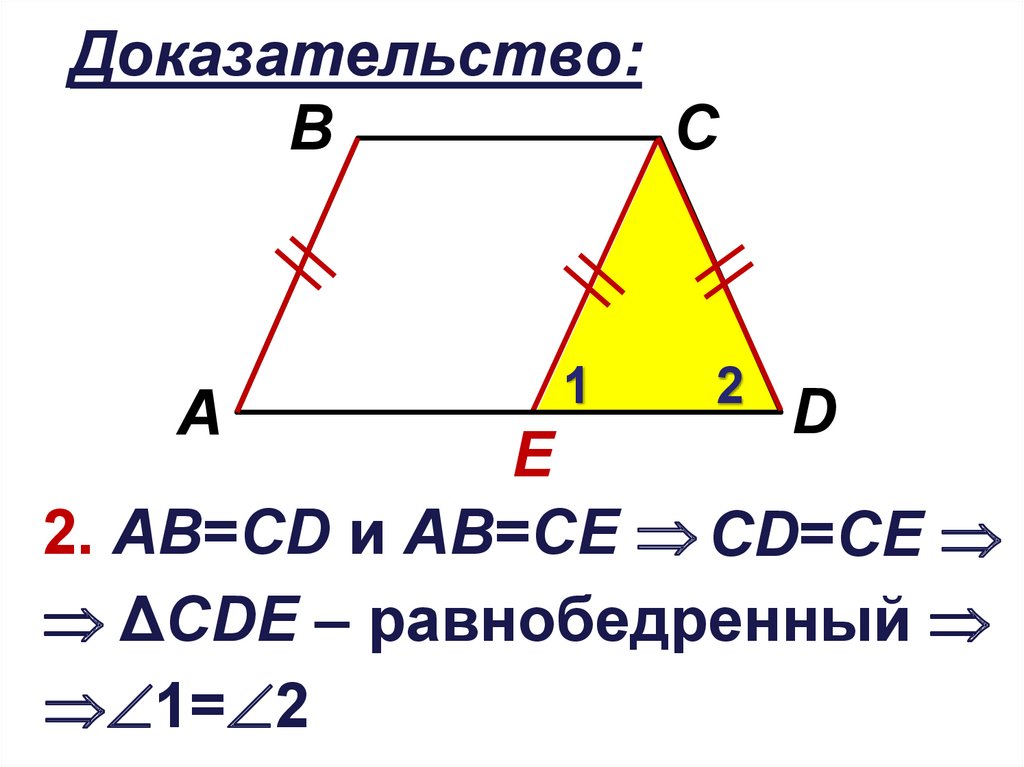
11.

Доказательство:
B
C
A
1
2
D
E
2. АВ=CD и АВ=СЕ CD=СЕ
ΔCDЕ – равнобедренный
1= 2

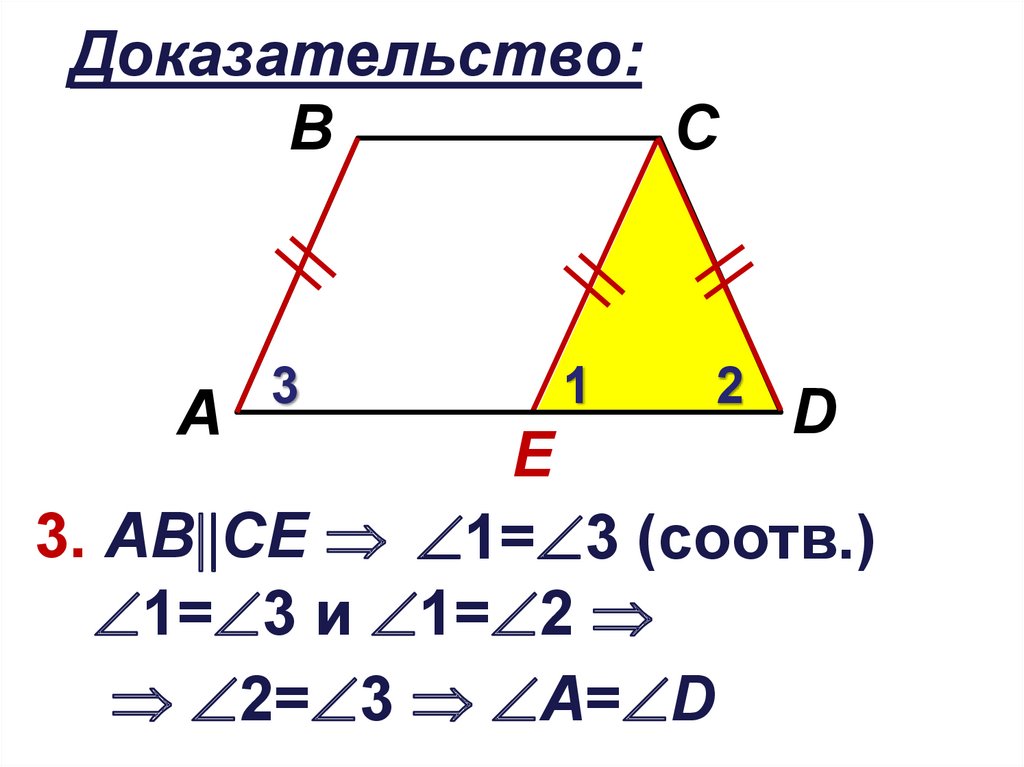
12.

Доказательство:
B
C
A
3
1
2
D
E
3. АВ CЕ 1= 3 (соотв.)
1= 3 и 1= 2
2= 3 А= D

13.

Доказательство:
B
C
A
3
1
E
4. АВC = 1800 – А
ВCD = 1800 – D
А= D
АВC = ВCD
2
D

14.

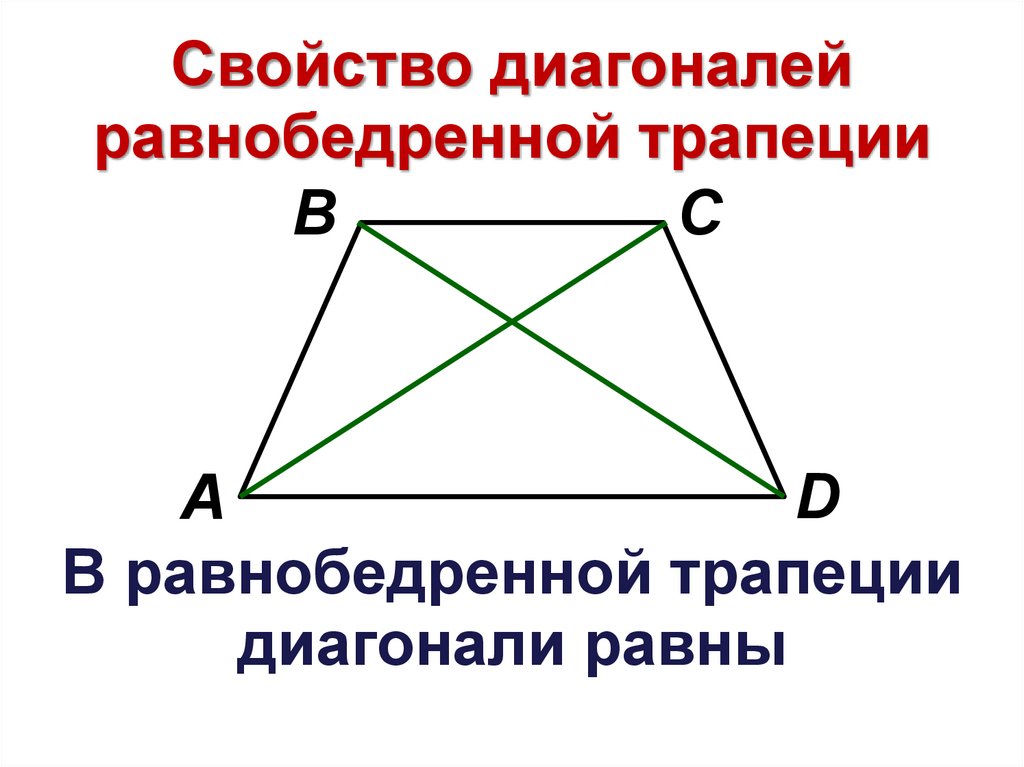
Свойство диагоналей
равнобедренной трапеции
B
C
D
A
В равнобедренной трапеции
диагонали равны

15.

B
A
C
D
Дано: ABCD –
равнобедренная трапеция
Доказать: АС = ВD

16.

Доказательство:
B
A
C
D
1. Рассм. ΔАВС и ΔВCD
АB=CD – по опр. равноб. трап.
АВС = BCD по св. углов трап.
ВС – общая

17.

Доказательство:
B
A
C
D
2. ΔАВС = ΔВCD по 2 сторонам
и углу между ними АC = BD
(чтд)

18.

Свойства равнобедренной
трапеции
1. В равнобедренной
трапеции углы при каждом
основании равны
2. В равнобедренной
трапеции диагонали равны

19.

Признаки равнобедренной
трапеции
1. Если углы при каждом
основании трапеции
равны, то она
равнобедренная
2. Если диагонали трапеции
равны, то она
равнобедренная

20. Задача 1

Найдите углы М и Р
трапеции MNPQ с
основаниями MQ и NP, если
0
0
N = 109 , а Q = 37

21.

Задача 2
Найдите основание AD
равнобедренной трапеции
ABCD, если
ВС = 10 см, АВ = 12 см,
D = 600

22.

Домашнее задание
1. Определение, свойства и
признаки параллелограмма и
трапеции выучить
2. Решить задачи из учебника:
№ 375, № 380, № 387, № 390
3. Решить 3 задачи по карточке
(выбрать задачи только одного
уровня по своим силам!)

23.

Список литературы
1. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.
и др. Геометрия: Учебник для 7-9 кл.
средней школы. Москва, 2014 г.
2. Гаврилова Н.Ф. Поурочные разработки по
геометрии: 8 класс.– М.: ВАКО, 2010. (В
помощь школьному учителю).
3. Ершова А.П., Голобородько В.В.,
Крижановский А.Ф. Тетрадь – конспект по
геометрии для 8 класса. – М.: ИЛЕКСА,
2015.