Решение систем уравнений методом введения новой переменной (9 класс)

1. Решение систем уравнений методом введения новой переменной 9 класс

2. Алгоритм работы с системой уравнений

Определите, какой метод удобнее
использовать при решении данной системы
уравнений
А) метод сложения
Б) метод подстановки
В) метод введения новой переменной
(используем при условии, что применить
пункт А или Б сложно).

3. Система уравнений и её решение

Что называется решением
системы с двумя переменными?
Что значит решить систему
уравнений с двумя переменными?

4. Система уравнений и её решение

Решением системы уравнений с двумя
переменными называется пара значений
переменных,
обращающая
каждое
уравнение системы в верное равенство.
Решить систему уравнений - это значит
найти все её решения или установить, что
их нет.

5. Подготовительная работа:

Повторите решение уравнений методом
введения новой переменной.
Материал 8 класса или посмотрите видеоурок:
https://www.youtube.com/watch?v=WCTj1KpyqTg

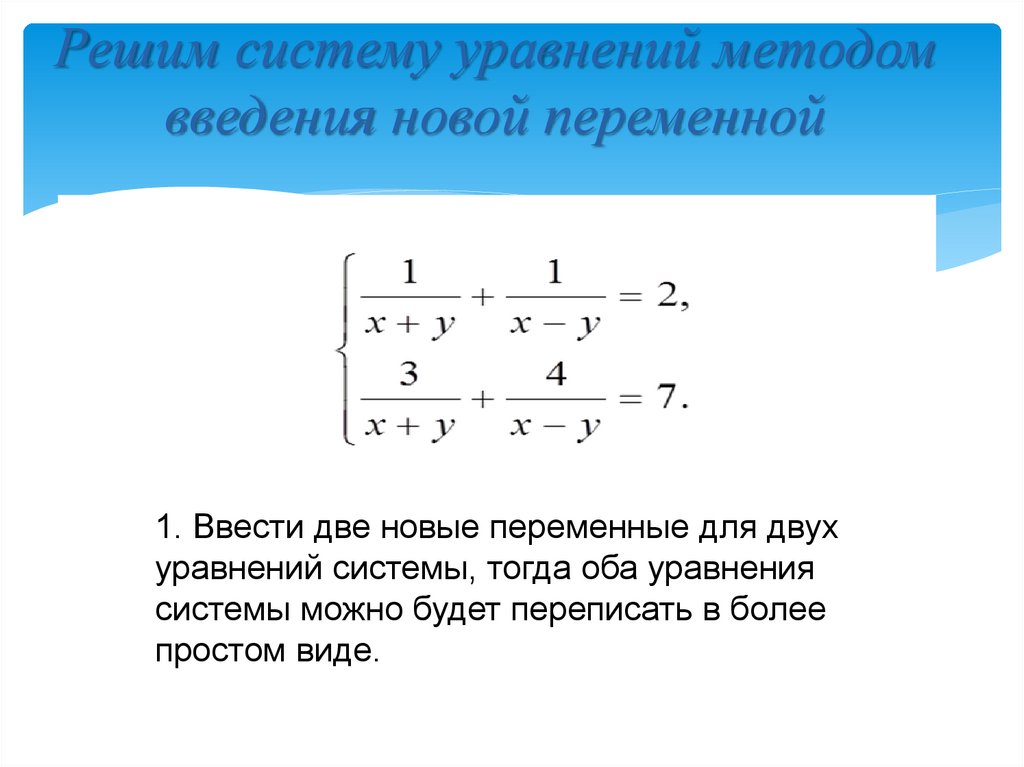
6. Решим систему уравнений методом введения новой переменной

1. Ввести две новые переменные для двух
уравнений системы, тогда оба уравнения
системы можно будет переписать в более
простом виде.

7. Решим систему уравнений методом введения новой переменной

1. Ввести две новые переменные для двух
уравнений системы, тогда оба уравнения
системы можно будет переписать в более
простом виде.
Пусть
1
a
x y
тогда
1
b
x y
a b 2,
3a 4b 7;

8. Решим систему уравнений методом введения новой переменной

2. Решить новую полученную систему с новыми
неизвестными удобным способом (сложения или
подстановки).
a b 2,
3a 4b 7;
a 2 b,
a 2 b, a 1,
3(2 b) 4b 7 b 1;
b 1.

9.

Вернемся к подстановке:
1
x y 1,
1 1;
x y
x y 1,
x y 1;
2 x 2, x 1, x 1,
x y 1; 1 y 1; y 0.
Ответ (1;0).
3. Подставить каждый корень,
найденный на втором шаге, в
две веденных постановки.
4. Записать поочередно
полученные уравнения в
систему.
5. Решить полученную систему
уравнений удобным
способом(методом сложения
или подстановки).
6. Записать все пары полученных
значений
системы в ответ.