Теорема о трех перпендикулярах

1.

1. Посмотреть фрагмент урока по предложенной ссылке.
2. Записать содержание слайдов 2-6 в тетради, заменив многоточие на
символическую запись, соответствующую содержанию текста
доказательства или решения.
3. Запомнить оформление обоснования для теоремы о трех перпендикулярах в
задачах ( пункт 4(задача 1) и пункт 3(задача 2)).

2.

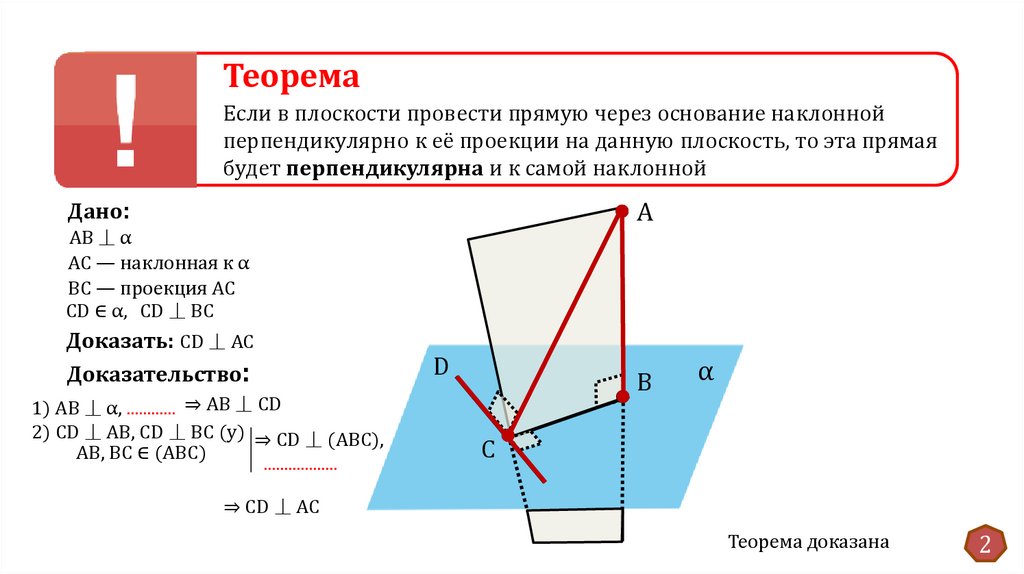
Теорема
Если в плоскости провести прямую через основание наклонной
перпендикулярно к её проекции на данную плоскость, то эта прямая
будет перпендикулярна и к самой наклонной
Дано:
A
AB ⏊ α
АС — наклонная к α
ВС — проекция АС
СD ∈ α, CD ⏊ BC
Доказать: CD ⏊ AC
Доказательство:
1) AB ⏊ α, ............ ⇒ AB ⏊ CD
2) CD ⏊ AB, CD ⏊ BC (у) ⇒ CD ⏊ (ABC),
AB, BC ∈ (ABC)
..................
D
B
α
C
⇒ CD ⏊ AC
Теорема доказана
2

3.

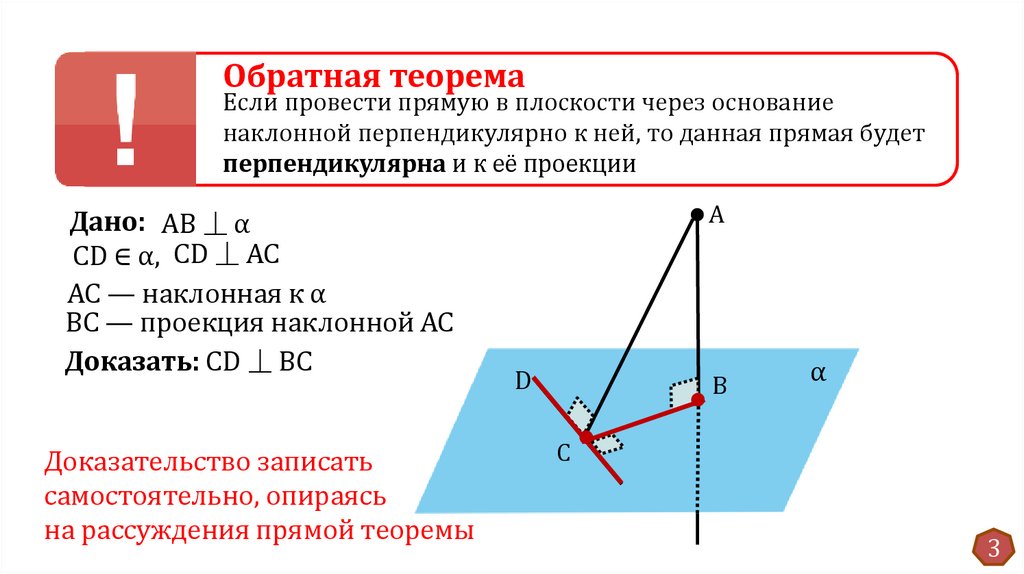
Обратная теорема
Если провести прямую в плоскости через основание
наклонной перпендикулярно к ней, то данная прямая будет
перпендикулярна и к её проекции
Дано: AB ⏊ α
СD ∈ α, CD ⏊ AC
АС — наклонная к α
ВС — проекция наклонной АС
Доказать: CD ⏊ BC
Доказательство записать
самостоятельно, опираясь
на рассуждения прямой теоремы
A
D
B
α
C
3

4.

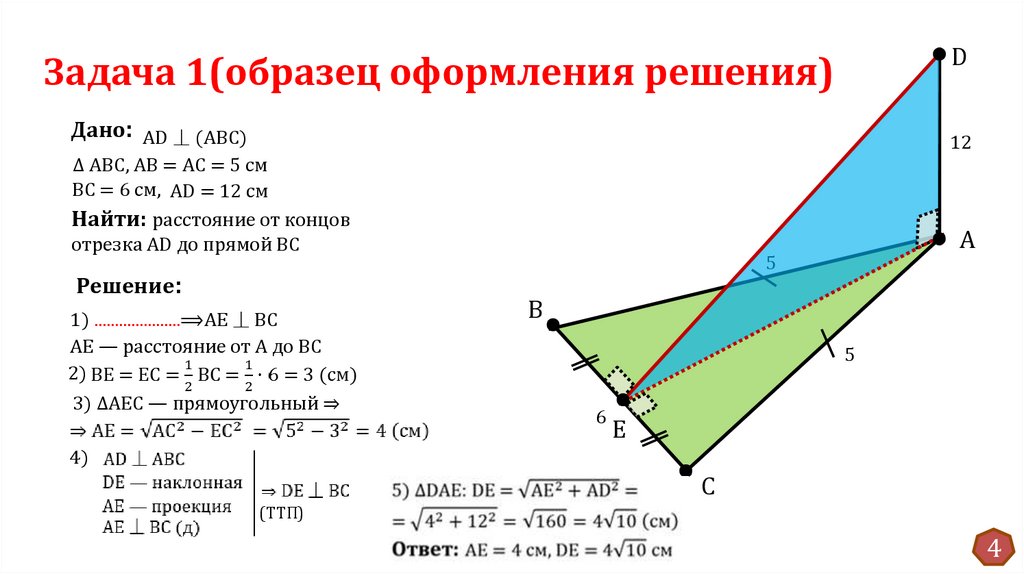
D
Задача 1(образец оформления решения)
Дано: AD ⏊ (ABC)
12
∆ ABC, AB = АC = 5 см
ВС = 6 см, AD = 12 см
Найти: расстояние от концов
отрезка AD до прямой ВС
Решение:
1) .....................⟹AE ⏊ BC
AE — расстояние от А до BC
2)
3) ∆АЕС — прямоугольный ⇒
A
5
B
5
6
E
4)
C
(ТТП)
4

5.

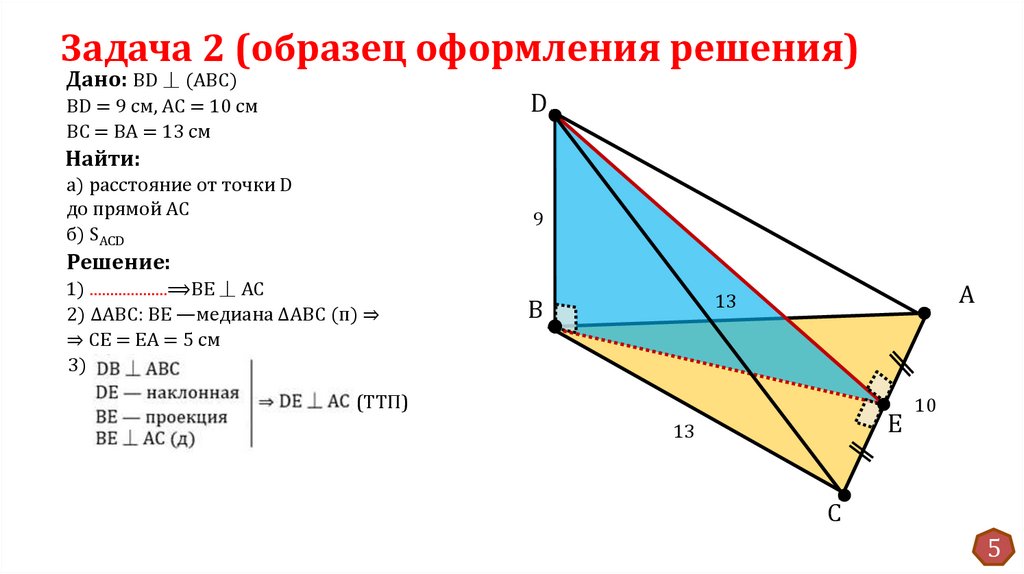
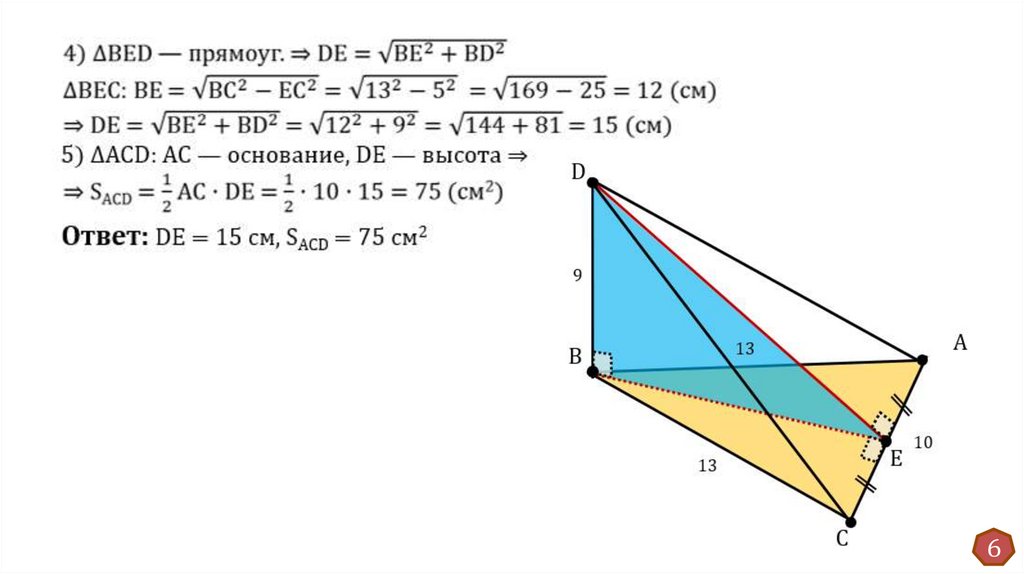
Задача 2 (образец оформления решения)
Дано: BD ⏊ (ABC)
D
ВD = 9 см, АС = 10 см
ВС = ВА = 13 см
Найти:
a) расстояние от точки D
до прямой AС
б) SACD
9
Решение:
1) ...................⟹BE ⏊ AC
2) ΔАВС: BЕ —медиана ΔАВС (п) ⇒
⇒ СЕ = ЕА = 5 см
3)
A
13
B
(ТТП)
E
13
10
C
5

6.

6