Решение неравенств второй степени

1.

Тема: «Решение неравенств
второй степени»

2.

у
у = х2 – 3х
9
8
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
о
Решите неравенство
х2 – 3х 0
-1
-2
1
2
3
4
5
6
7
х
-3
-4
-5
-6
Ответ : ( ;0] [3; )

3.

у
9
8
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
о
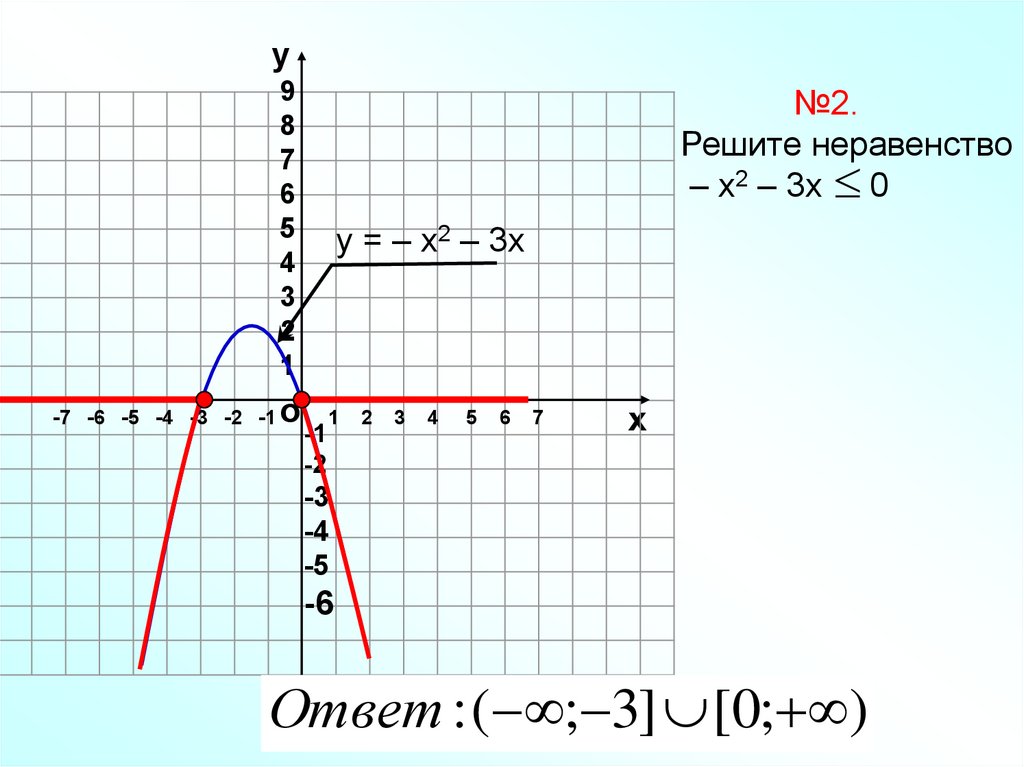
№2.
Решите неравенство
– х2 – 3х 0
у = – х2 – 3х
-1
-2
1
2
3
4
5
6
7
х
-3
-4
-5
-6
Ответ : ( ; 3] [0; )

4.

у
9
8
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
о
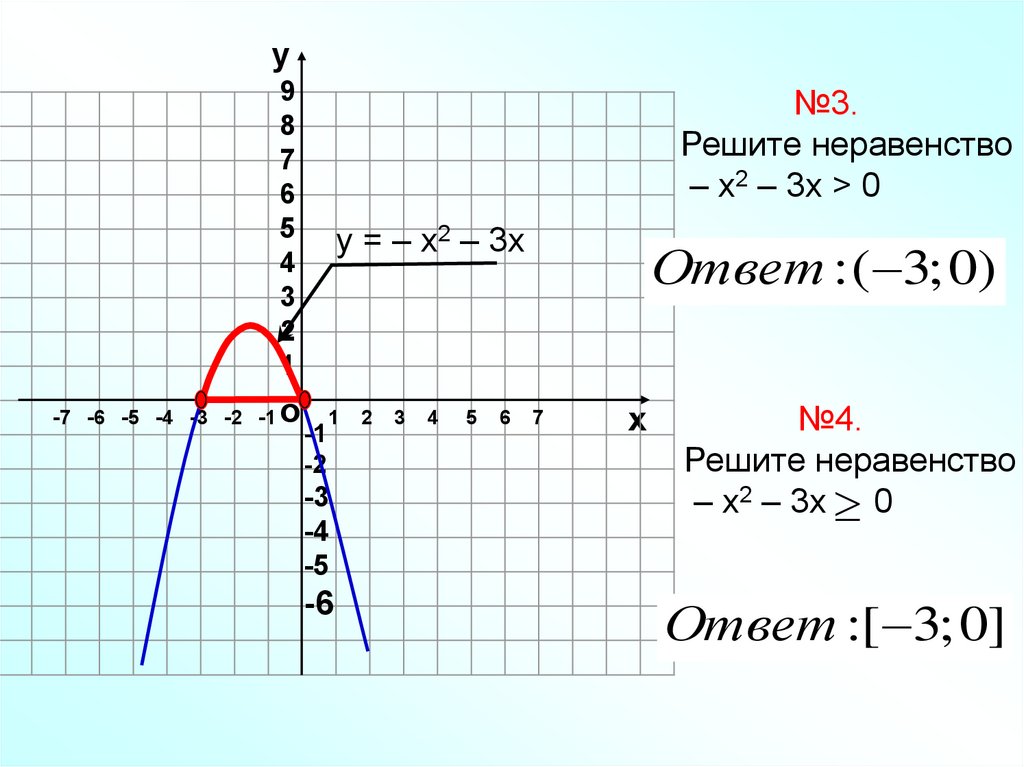
№3.
Решите неравенство
– х2 – 3х > 0
у = – х2 – 3х
-1
-2
1
-3
-4
-5
-6
2
3
4
5
6
Ответ : ( 3; 0)
7
х
№4.
Решите неравенство
– х2 – 3х 0
Ответ :[ 3; 0]

5.

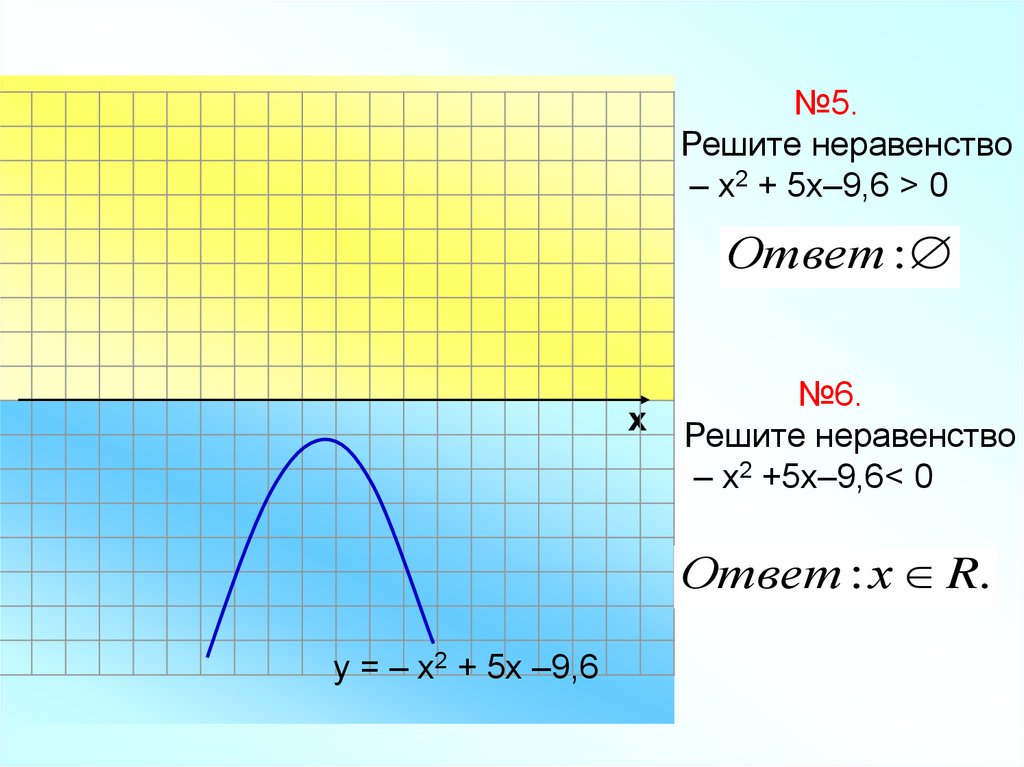
№5.
Решите неравенство
– х2 + 5х–9,6 > 0
Ответ :
х
№6.
Решите неравенство
– х2 +5х–9,6< 0
Ответ : х R.
у = – х2 + 5х –9,6

6.

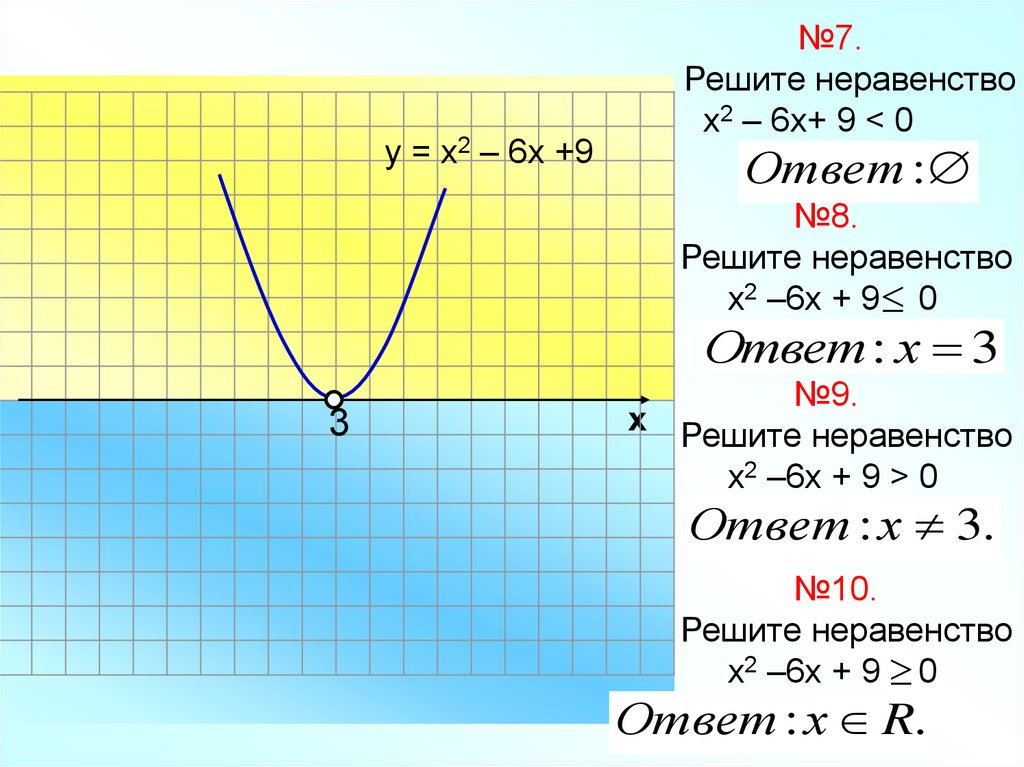
у = х2 – 6х +9
№7.
Решите неравенство
х2 – 6х+ 9 < 0
Ответ :
№8.
Решите неравенство
х2 –6х + 9 0
Ответ : х 3
3
№9.
х Решите неравенство
х2 –6х + 9 > 0
Ответ : х 3.
№10.
Решите неравенство
х2 –6х + 9 0
Ответ : х R.

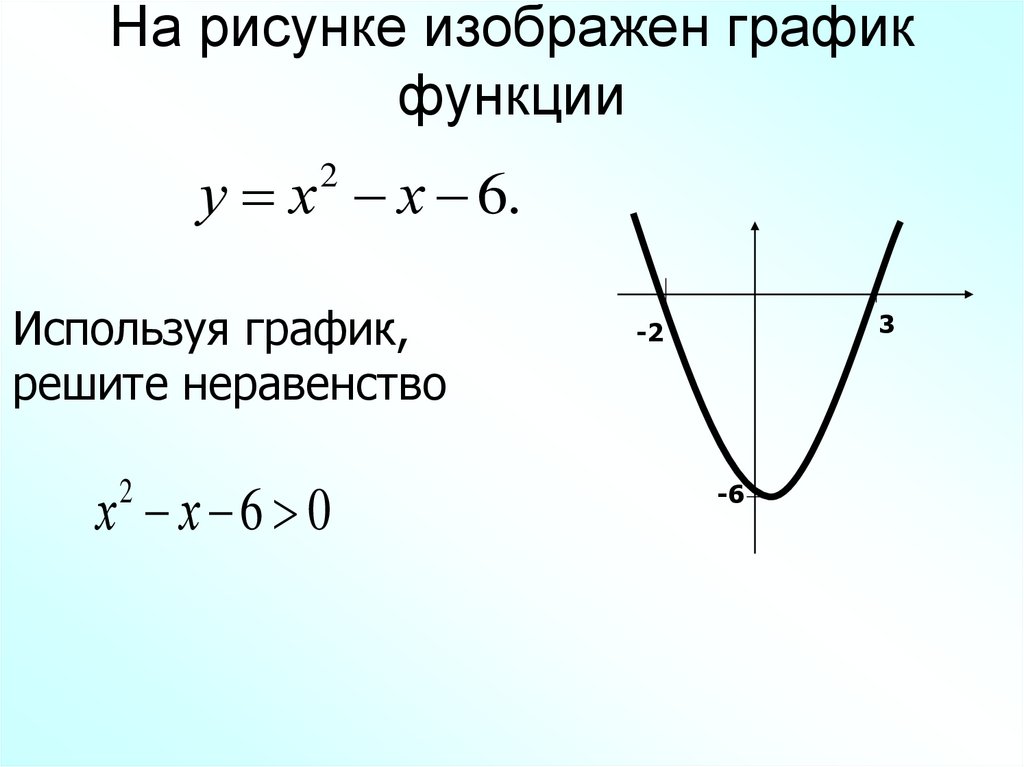
7. На рисунке изображен график функции

у х х 6.
2
Используя график,
решите неравенство
х х 6 0
2
3
-2
-6

8.

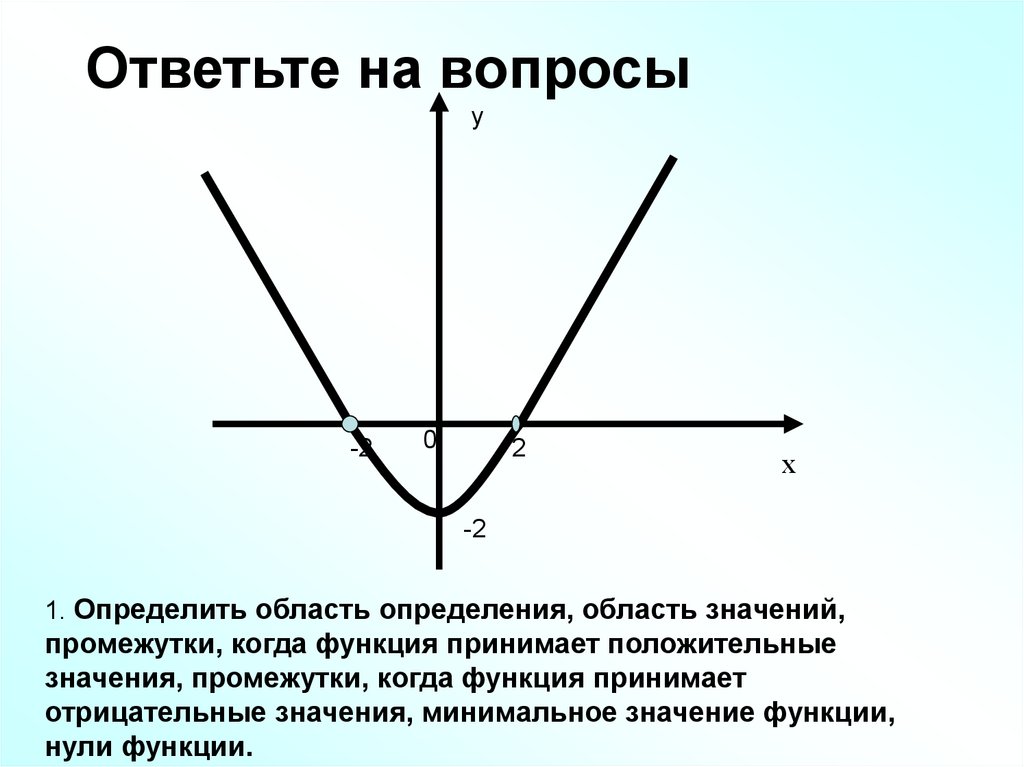
Ответьте на вопросы
у
-2
0
2
х
-2
1. Определить область определения, область значений,
промежутки, когда функция принимает положительные
значения, промежутки, когда функция принимает
отрицательные значения, минимальное значение функции,
нули функции.

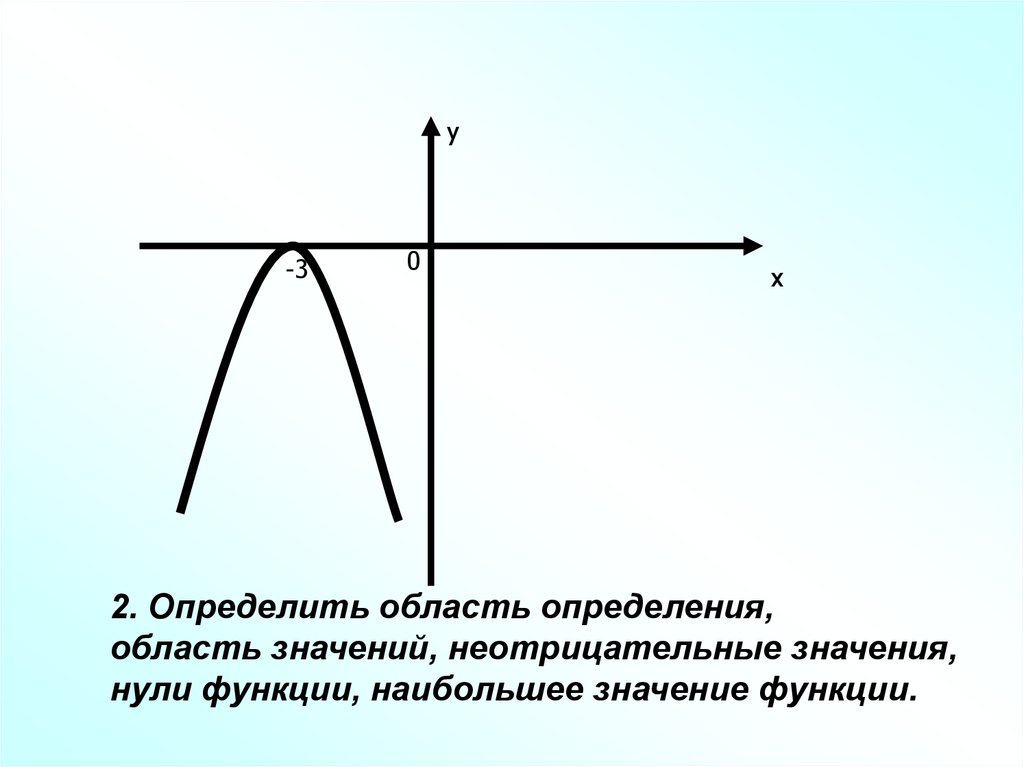
9.

у
-3
0
х
2. Определить область определения,
область значений, неотрицательные значения,
нули функции, наибольшее значение функции.

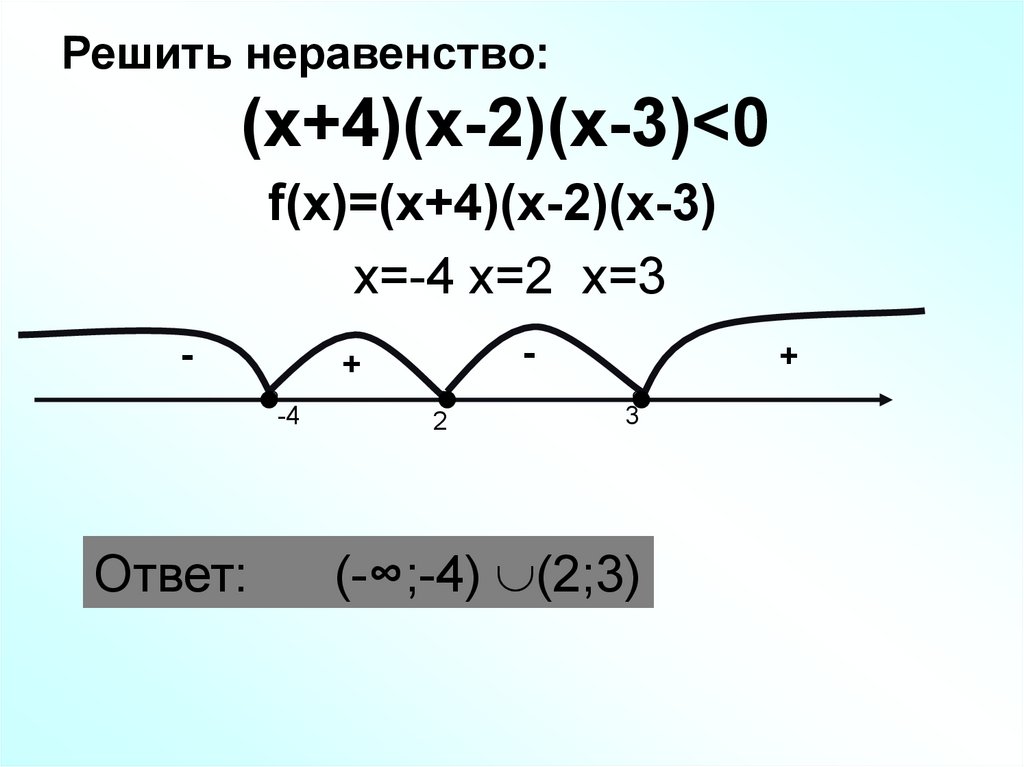
10. (х+4)(х-2)(х-3)<0

Решить неравенство:
(х+4)(х-2)(х-3)<0
f(х)=(х+4)(х-2)(х-3)
х=-4 х=2 х=3
-4
Ответ:
-
+
2
+
3
(-∞;-4) (2;3)

11. Решить неравенство

• (10х+3)(17-х)(х-5)≥0

12.

х 5
<0
х 6
Решение: равносильно: (х-5)(х+6)<0
1.Рассмотрим функцию f(х)=(х-5)(х+6)
2.Нули функции х=5, х=-6
Ответ: (-6;5).

13.

Найти область определения функции:
У=
( х 12)( х 1)( х 9)
(х+12)(х-1)(х-9)≥0
Ответ: [-12;1] [9;+ ).

14. Найти область определения функции:

Сделайте cамостоятельно
• у= (2х 5)( х 17)
у= ( х 9)(2х 8)

15.

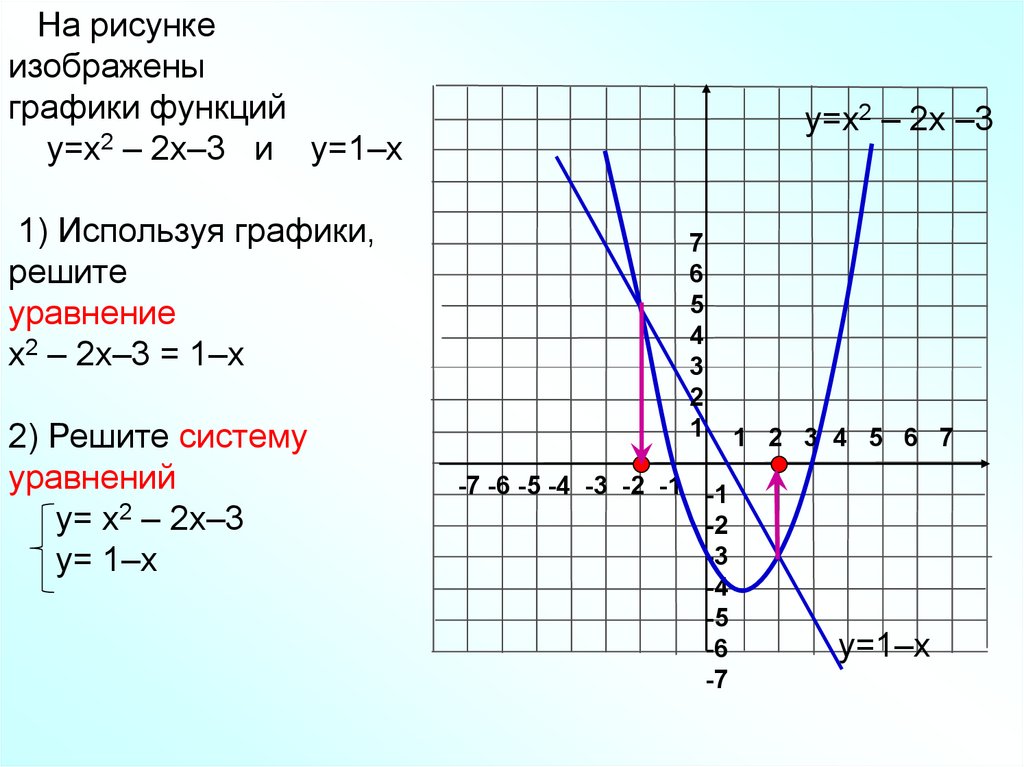
На рисунке
изображены
графики функций
у=х2 – 2х–3 и у=1–х
1) Используя графики,
решите
уравнение
х2 – 2х–3 = 1–х
2) Решите систему
уравнений
у= х2 – 2х–3
у= 1–х
у=х2 – 2х –3
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1 -1
-2
-3
-4
-5
-6
-7
1 2 3 4 5 6 7
у=1–х