Похожие презентации:
Основное свойство первообразной
1.
Основное свойствопервообразной
2. ЗАДАНИЕ
1. Повторить, слайд №3,4,6,72.Слайд №8,9 рассмотреть
примеры нахождения
первообразных
3.Решить самостоятельно, слайд
№10
3. Теорема:
Любая первообразная дляфункции
f на промежутке может быть
записана в виде
F(х)+С, где
F(х) одна из первообразных
для f(х)
С – произвольная постоянная
4. Доказательство:
По определению первообразнойF'(х) = f(х), проверим
(F(х)+С)‘ = f(х) + 0
Ч.т.д
5.
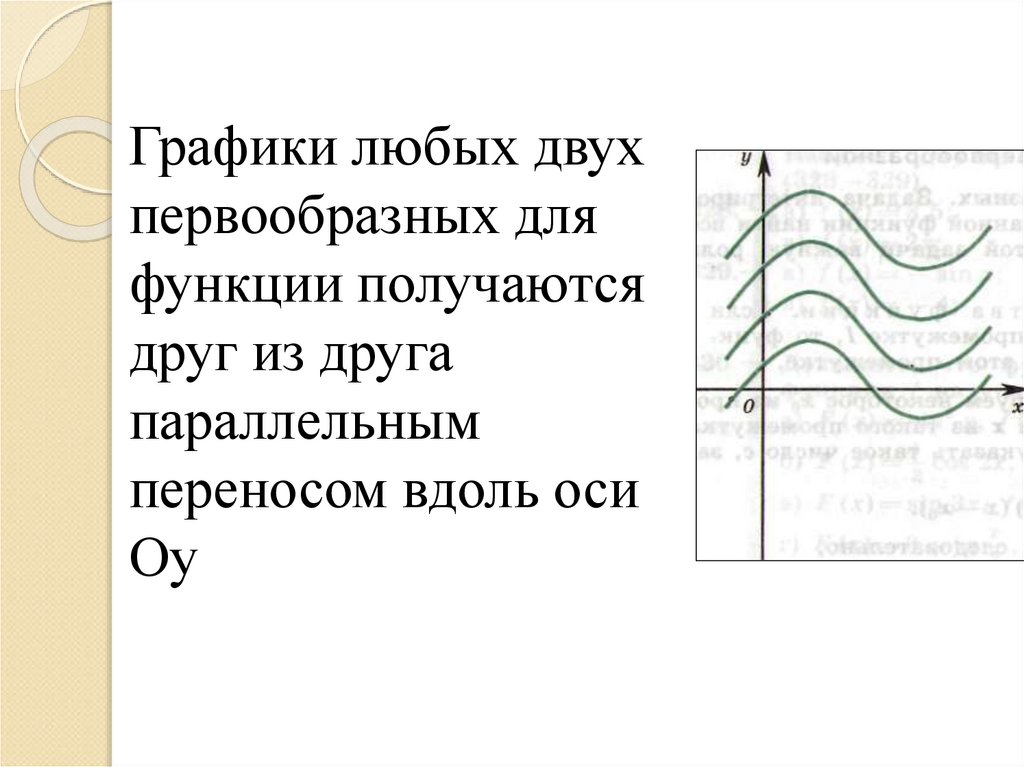
Графики любых двухпервообразных для
функции получаются
друг из друга
параллельным
переносом вдоль оси
Оу
6.
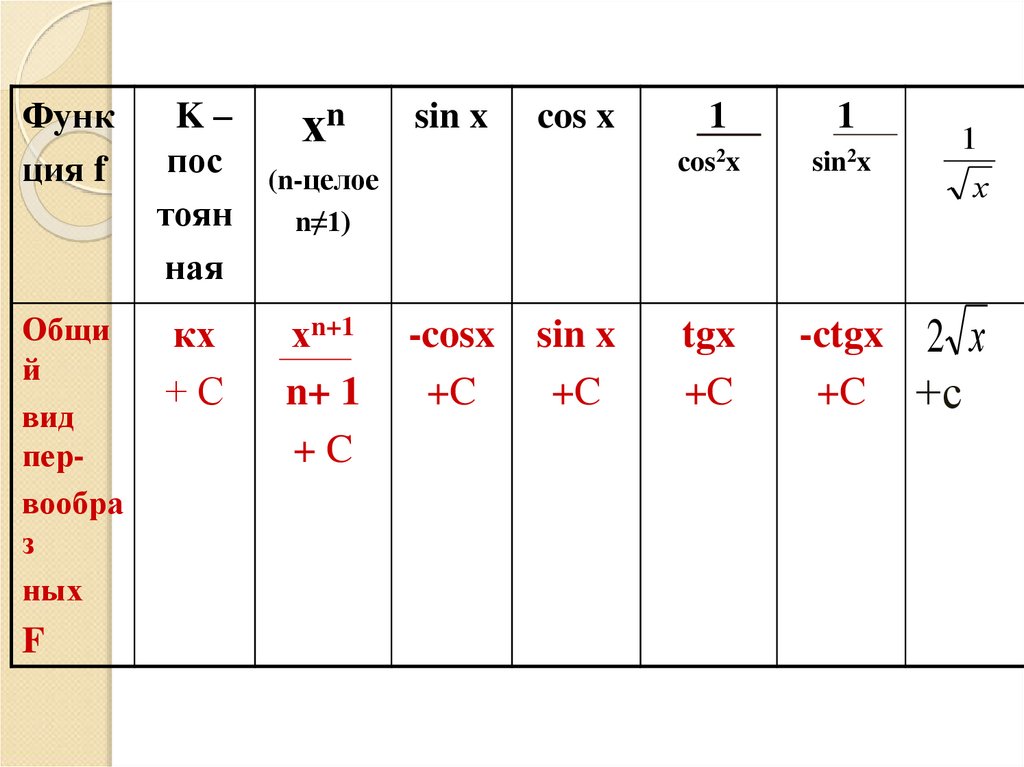
Функция f
K–
пос
тоян
ная
Общи
й
вид
первообра
з
ных
кх
+С
F
хn
sin x
cos x
сos2x
(n-целое
n≠1)
хn+1
n+ 1
+C
1
-cosx
+C
sin x
+C
tgx
+C
1
sin2x
1
х
-ctgx 2 х
+C +с
7. Запомни!
Первообразная для f(х)обозначается F(х)
8. Найдите первообразные
Пример №1. f(х) = 4Смотрим в верхнюю строку таблицы,
первый столбик. Там написано к –
постоянная. Опускаемся во вторую строку,
там написано кх. Вместо к ставим наше
число 4, будет F(х) = 4х + С
Аналогично, для f(х) =-5, F(х) = -5х + С
9.
Пример №2. f(х) = х2Смотрим в верхнюю строку таблицы,
второй столбик. Там написано хn ,у нас
n = 2. Опускаемся во вторую строку, там
написано хn/n+1. Вместо n ставим наше
число , будет F(х) = х2+1/2 +1+С=х3/3 +С
Аналогично для f(х) =х3, F(х) = х4/4 + С
10. Найдите первообразные
1.f(х) =102.f(х) = -3
3.f(х) =х-5;
4. f(х) =х-6;
5.f(х) =х-8;
7. f(х) = 12
7.f(х) = 7
8. f(х) = х9;
9. f(х) =х4
11. Найдите первообразные
16.f(х) =х7 - 10;17. f(х) =х3 + sin x+ 2;
18.f(х) =х8;
19. f(х) = sin x + 5;
20.f(х) = cos x;
21. f(х) = х2+1;
22. f(х) =х9 + 30.
12.
23.f(х) =4;24. f(х) =-5;
25.f(х) =10;
26. f(х) =9;
27.f(х) =х2;
28.f(х) =х3;
29.f(х) =х5;
30.f(х) =х9;
31.f(х) =х-5;
32. f(х) =х10;
33.f(х) =х-8;
34.f(х) = sin x;
35.f(х) = cos x;









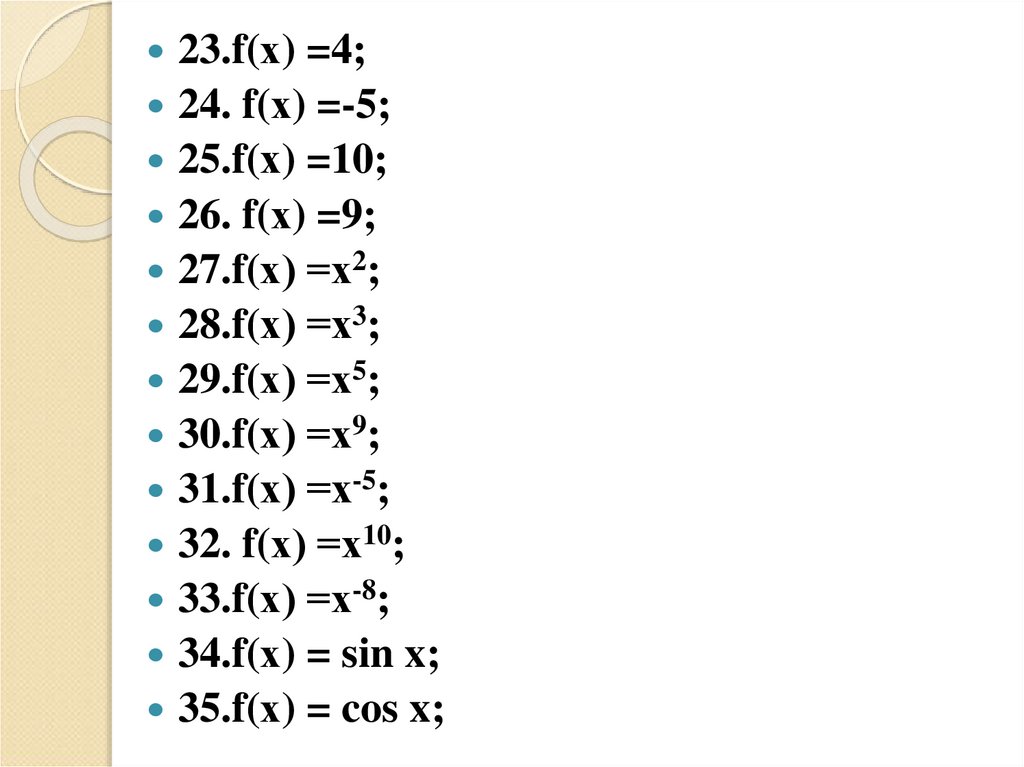

 Математика
Математика








